随着半导体制程工艺的进一步缩小、多电平存储技术的使用,存储单元成本大幅下降,NAND固态数据存储已广泛应用于各种消费类电子产品及部分数据中心。对于NAND闪存器件,存储密度提升的同时,存储单元受到的噪声干扰进一步加剧,导致数据存储可靠性降低[1]。一般数据存储误码率要求必须低于10−15。相较于使用硬判决译码方法的Bose-Chaudhuri-Hocquenghem (BCH) 纠错码,低密度奇偶校验(low-density parity-check, LDPC)纠错码使用软判决译码方法,能极大地降低误码率[2]。多种噪声引起阈值电压偏移而产生误读数据,单元间干扰[3]和持久性噪声[4]是制约NAND闪存数据存储可靠性的主要噪声。目前,为了补偿噪声对阈值电压的影响,闪存采用重读机制[5−8]。动态优化读参考电压[7−11]以适应阈值电压的偏移,采用优化的读参考电压可以获得最低的原始误码率,从而达到改善存储可靠性的目的。在读电压检测范围内,Cai等[7]提出等间隔降低读参考电压操作,该方案可以降低阈值电压检测的范围。
针对阈值电压检测时读操作带来的时延问题,通过对重叠区的原始误码率分析,本文提出了非均匀迭代更新读电压优化方案,该方案有效地降低了读操作的次数。
1 阈值电压检测 1.1 系统模型数据闪存系统模型如图1所示,数据经过LDPC编码后通过编程和擦除操作写入闪存单元;经过信道噪声干扰后(单元间干扰和持久性噪声),单元阈值电压产生偏移造成数据误读,需要进行信道检测优化;读操作得到单元对应的对数似然比信息,再通过LDPC译码算法进行纠错处理[1−2,12]。

|
Download:
|
| 图 1 系统模型 | |
1)擦除操作:数据写入单元前必须要先擦除。擦除状态的阈值电压服从高斯分布。擦除状态的阈值电压概率密度函数如下:
| ${p_{\rm{e}}}\left( x \right) = \frac{1}{{{\sigma _{\rm{e}}}\sqrt {2{\text{π}}} }}{{\rm{e}}^{ - \frac{{\left( {x - {\mu _{\rm{e}}}} \right)}}{{2\sigma _e^2}}}}$ |
式中
2)编程操作:ISPP技术应用于写入数据。擦除状态的阈值电压服从均匀分布。第
| $p_{\rm{p}}^k(x) = \left\{ \begin{array}{l} \dfrac{1}{{\Delta {V_{\rm{pp}}}}},\;\;\; \;V_{\rm{p}}^k \leqslant x \leqslant V_{\rm{p}}^k + \Delta {V_{\rm{pp}}} \\ 0,\;\;\;{\text{其他}} \end{array} \right.$ |
式中:
3)单元间干扰(cell-to-cell interference, CCI):相邻单元间干扰是由于寄生电容耦合效应引起的,会使阈值电压向右偏移。
| $F = \sum {\Delta V_t^k} {\gamma ^k}$ |
式中:
4)持久性噪声(retention noise):持久性噪声是由于氧化层电荷泄露引起的,会使阈值电压向左偏移。持久性噪声服从高斯分布,概率密度函数建模如下:
| ${p_{\rm{r}}}\left( x \right) = \frac{1}{{{\sigma _{\rm{r}}}\sqrt {2{\text{π}}} }}{{\rm{e}}^{ - \frac{{\left( {x - {\mu _{\rm{r}}}} \right)}}{{2\sigma _r^2}}}}$ |
式中
| ${\mu _{\rm{r}}} = (x - {x_0}) \cdot \left[ {{A_t}{{(P)}^{{\alpha _i}}} + {B_t}{{(P)}^{{\alpha _o}}}} \right] \cdot \log \left( {1 + T} \right)$ |
式中:
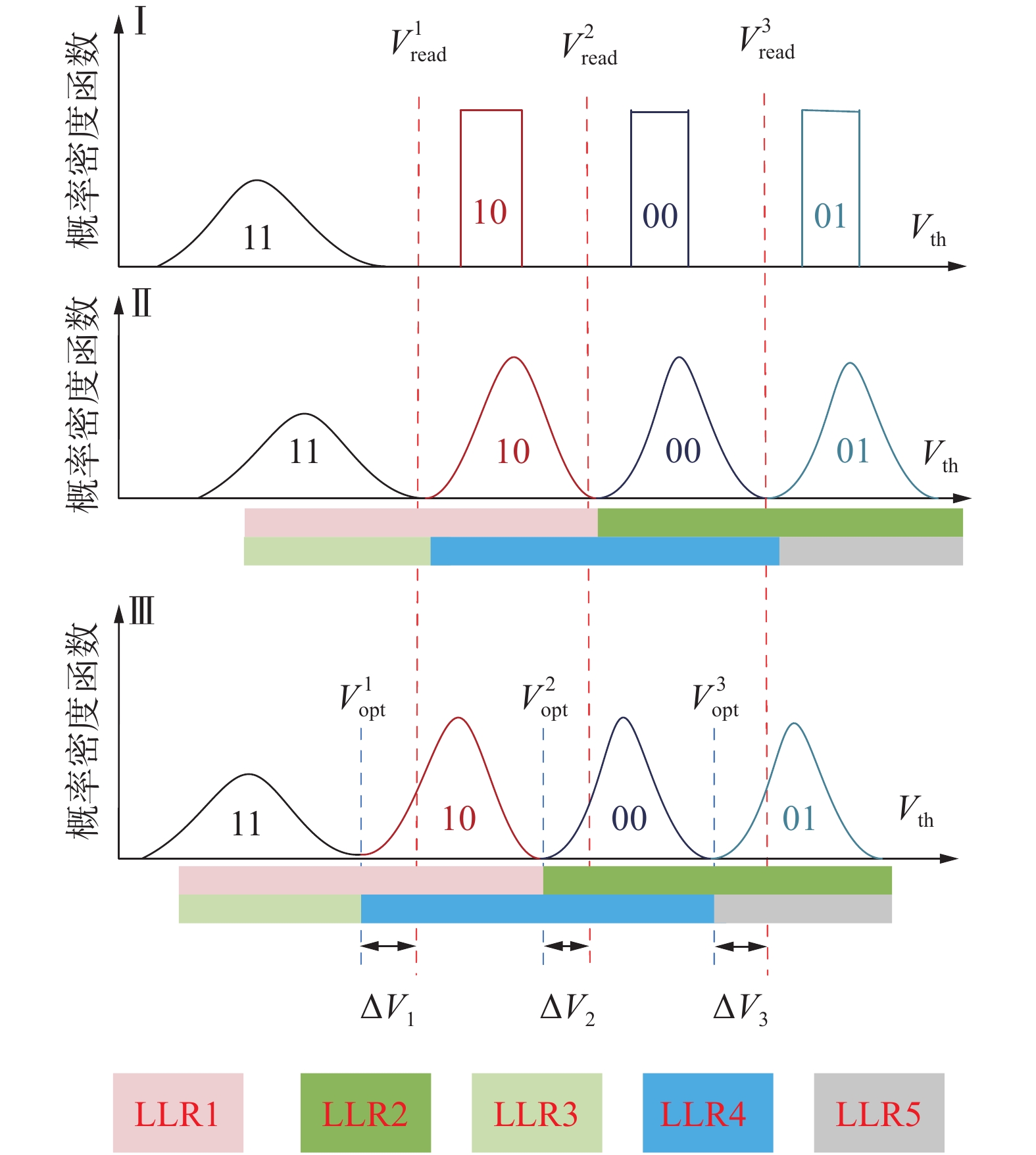
对于MLC型NAND闪存,每个单元写入2 bit信息,阈值电压被划分为4种存储状态(11,10,00,01)。如图2所示,Ⅰ表示经过编程和擦除操作后的阈值电压分布,进行数据写操作;Ⅱ表示经过单元间干扰,单元间干扰使阈值电压向右偏移,根据文献[3]进行对数似然比(log-likelihood-ratio, LLR)计算;Ⅲ表示经过持久性噪声,持久性噪声使阈值电压向左偏移,因此在电压重叠区上,传统的固定读参考电压
|
Download:
|
| 图 2 读电压优化 | |
当读取数据时,重读(read-retry)机制产生的全部时延[7]为:
| ${T_{{\rm{read}}}} = \sum\limits_{i = 1}^N {\left( {T_{{\rm{ECC}}}^i + {T_{{\rm{flash}}}}} \right)} $ | (5) |
式中:
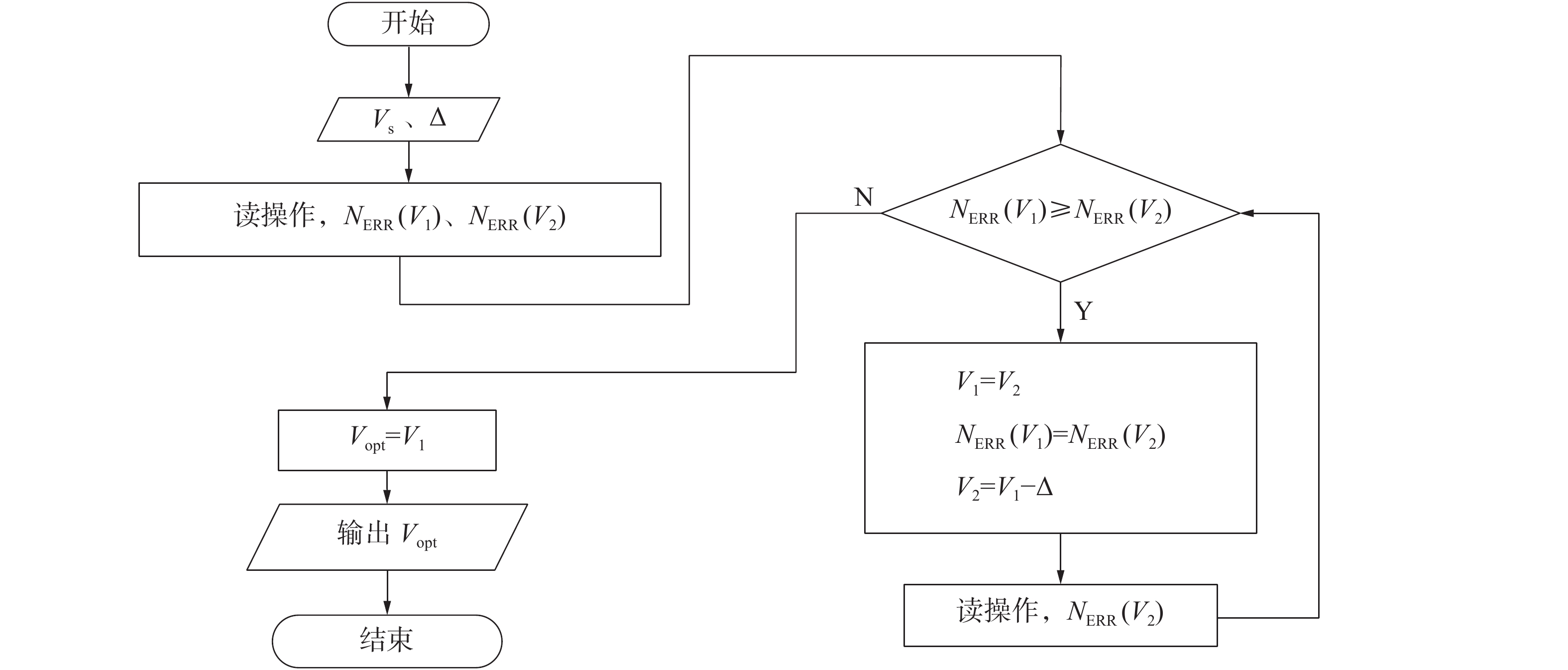
为了弥补噪声对信道的影响,选取低时延的ROR读电压优化技术[7],即原始误码率最低点作为优化读参考电压,算法流程如图3所示。
|
Download:
|
| 图 3 重读机制算法流程 | |
算法1 重读机制
输入:信道电压检测的上限
输出:优化后的读参考电压
Step0 初始化:
读操作,计算
Step1 While
While
更新:
读操作,计算
End
Step2
相邻存储状态重叠区的原始误码率分布情况如图4所示,

|
Download:
|
| 图 4 原始误码率分布情况 | |
|
Download:
|
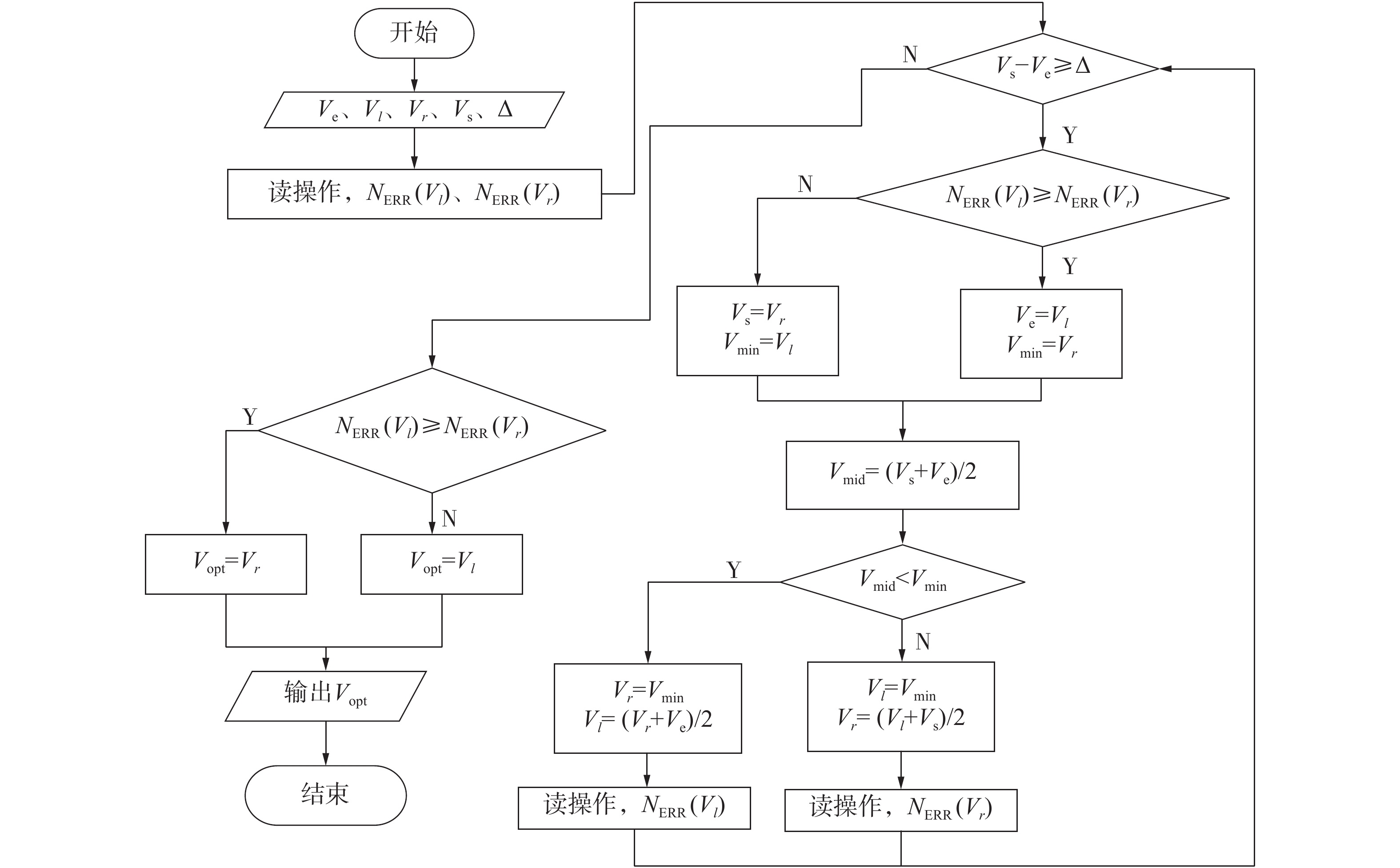
| 图 5 优化方案算法流程 | |
算法2 改进的重读机制
输入:信道电压检测的上限
输出:优化后的读参考电压
Step0 初始化:
读操作,计算
Step1 判断
Step2 判断
Step3 更新:
判断
Step4 更新:
判断
Step5 更新:
读操作,计算
Step6 更新:
读操作,计算
Step7 判断
其中,Step0初始化需要执行2次读操作;Step3表示如果
基于MATLAB平台对闪存信道建模仿真,参数如下:重叠区上信道检测范围
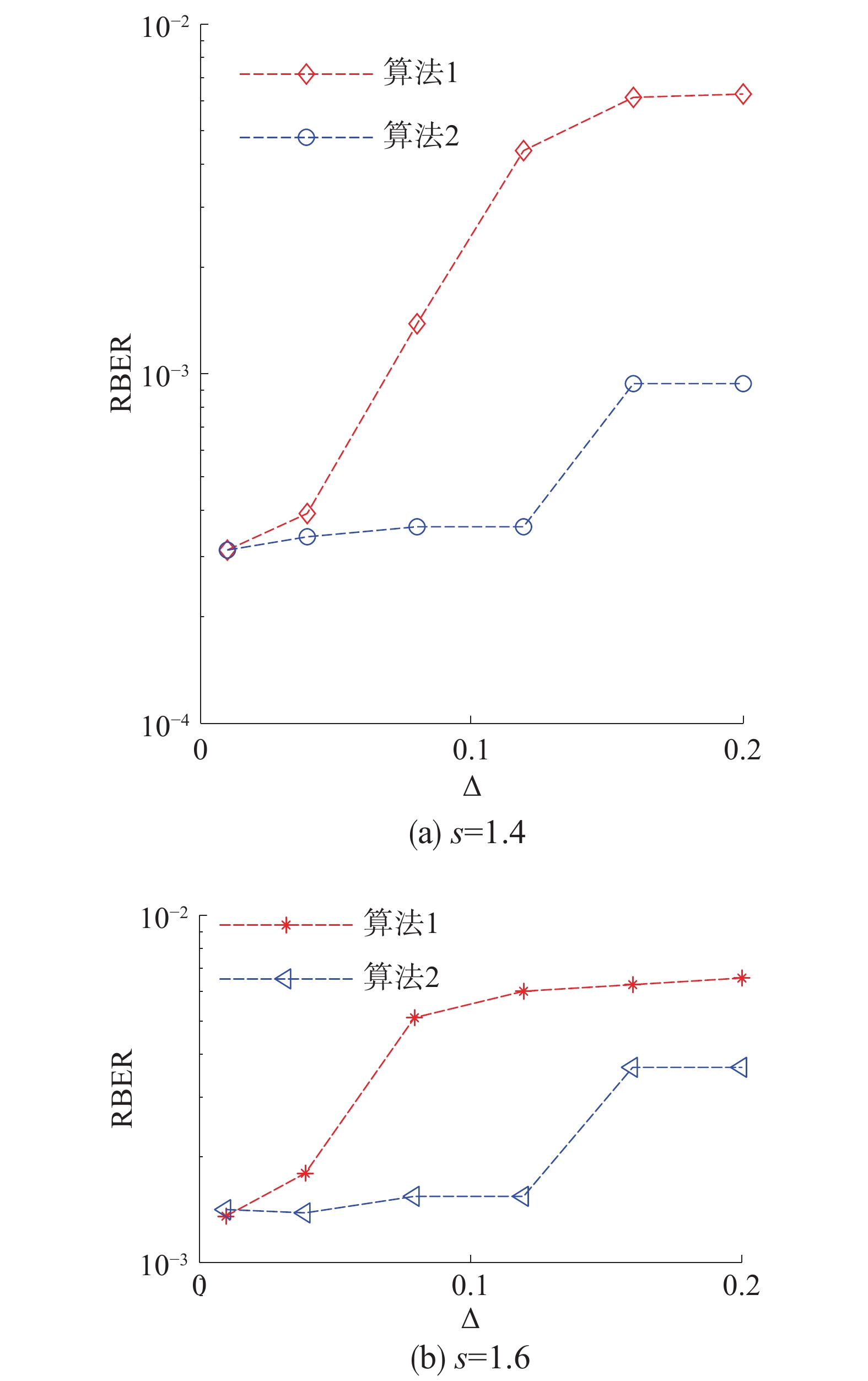
图6、7表示仿真不同的噪声环境下,所提出方案的可靠性。在单元间干扰下,图6表示不同的耦合强度因子
仿真结果显示:1)信道检测精度越高,误码率越低,数据存储可靠性越高;2)与算法1相比,在相同的检测精度下,改进的重读机制有更好的纠错性能。
|
Download:
|
| 图 6 单元间耦合因子s不同时的误码率 | |

|
Download:
|
| 图 7 持久性时间T不同时的误码率 | |
信道阈值电压检测精度越高,误码率越低,纠错性能越好,检测精度
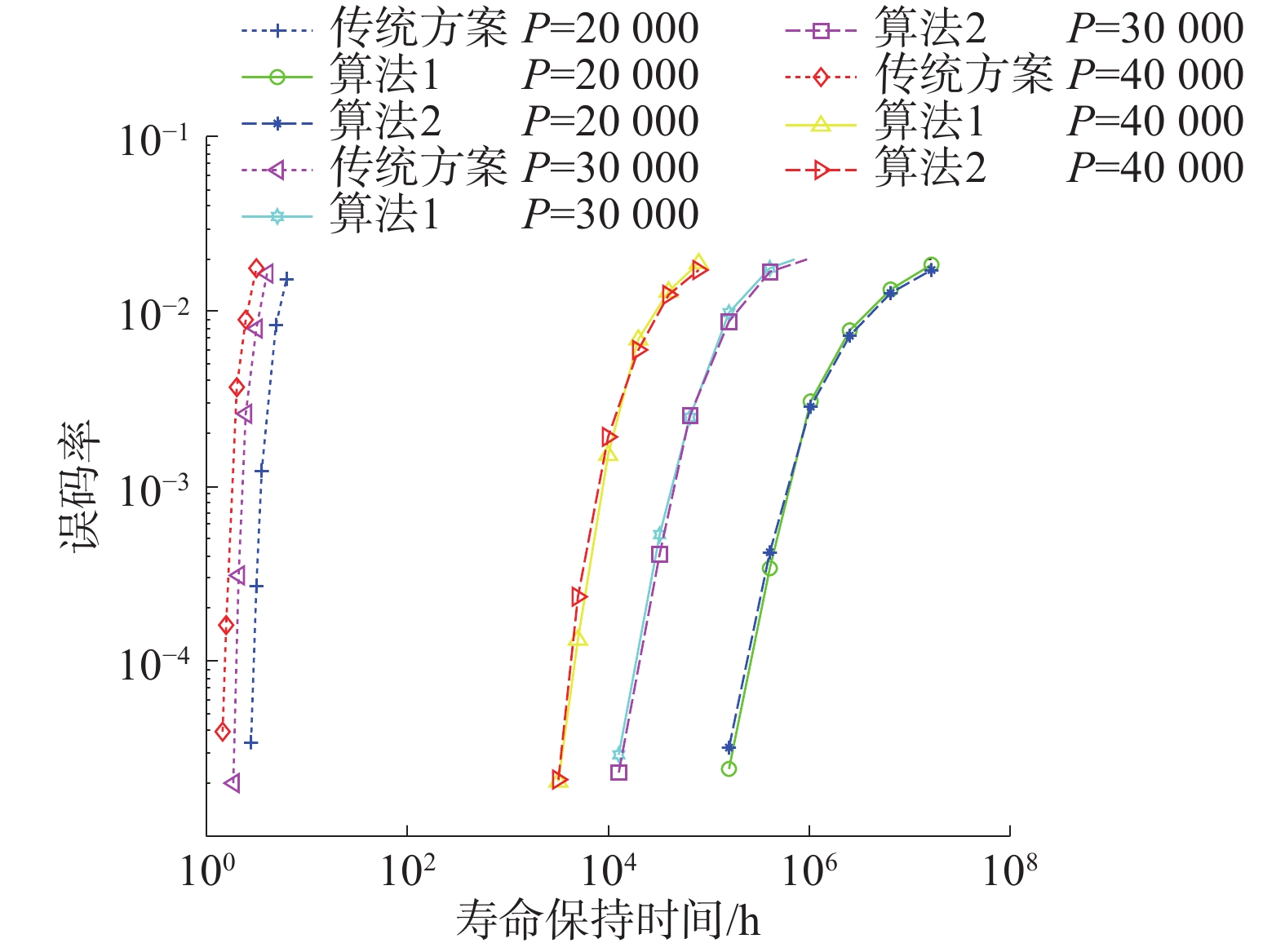
图8是在闪存信道下不同检测算法的误码率比较。仿真结果显示:1)相对于传统方案,采用阈值电压检测能有效地提升数据存储的可靠性;2)在高精度检测下,改进的重读机制不会有性能损失。
|
Download:
|
| 图 8 误码率性能比较 | |
阈值电压检测虽然带来了纠错性能的提升,但会产生较大的时延。读时延与读操作次数成正比,读操作次数越小,读时延越低。单元间耦合强度因子为1.4。相对于目前的重读机制,图9是在闪存信道中改进重读机制的时延降低率。

|
Download:
|
| 图 9 读时延性能比较 | |
仿真结果显示:1)相对于目前的重读机制,改进的重读机制具有更低的时延;2)随着噪声的增加,改进的重读机制具有更高的时延降低率;3)在高精度、大噪声闪存信道中,改进的重读机制具有更好的性能。
4 结论基于重叠区错误比特的分布特性,本文提出了一种低时延重读机制优化方案。该优化机制在保证数据可靠性的前提下,可以有效降低读操作次数,具有可行性。另一方面来说,闪存控制器需要执行较多的比较操作,会产生少量延时,但该操作不会对闪存芯片产生影响。通过上述的理论分析及数据仿真,得出以下结论:1)对比现有的重读机制,该优化方案可以有效地提高数据存储的可靠性;2)对比现有的重读机制,该优化方案可以降低大量时延;3)在实际应用方面,该方案具有一定的可行性。
| [1] |
周天伟. NAND闪存的软硬判决纠错码应用研究[D]. 西安: 西安电子科技大学, 2014.
( 0) 0)
|
| [2] |
唐锐. LDPC码的编译码算法研究[D]. 成都: 电子科技大学, 2018.
( 0) 0)
|
| [3] |
DONG Guiqiang, XIE Ningde, ZHANG Tong. On the use of soft-decision error-correction codes in nand flash memory[J]. IEEE transactions on circuits and systems I: regular papers, 2011, 58(2): 429-439. DOI:10.1109/TCSI.2010.2071990 ( 0) 0)
|
| [4] |
WANG Xueqiang, DONG Guiqiang, PAN Liyang, et al. Error correction codes and signal processing in flash memory[M]//STIEVANO I. Flash Memory, Flash Memories. [S.l.]: InTech, 2011.
( 0) 0)
|
| [5] |
FAN Zhengqin, CAI Guofa, HAN Guojun, et al. Cell-state-distribution-assisted threshold voltage detector for NAND flash memory[J]. IEEE communications letters, 2019, 23(4): 576-579. DOI:10.1109/COML.4234 ( 0) 0)
|
| [6] |
CAI Yu, LUO Yixin, GHOSE S, et al. Read disturb errors in mlc nand flash memory: characterization, mitigation, and recovery[C]//Proceedings of the 45th IEEE/IFIP International Conference on Dependable Systems and Networks. Rio de Janeiro, Brazil, 2015: 438−449.
( 0) 0)
|
| [7] |
CAI Yu, LUO Yixin, HARATSCH E F, et al. Data retention in MLC NAND flash memory: characterization, optimization, and recovery[C]//Proceedings of the IEEE 21st International Symposium on High Performance Computer Architecture (HPCA). Burlingame, USA, 2015: 551−563.
( 0) 0)
|
| [8] |
CAI Yu, GHOSE S, HARATSCH E F, et al. Error characterization, mitigation, and recovery in flash- memory-based solid-state drives[J]. Proceedings of the IEEE, 2017, 105(9): 1666-1704. DOI:10.1109/JPROC.2017.2713127 ( 0) 0)
|
| [9] |
ASLAM C A, GUAN Yongliang, CAI Kui. Read and write voltage signal optimization for multi-level-cell (MLC) NAND flash memory[J]. IEEE transactions on communications, 2016, 64(4): 1613-1623. DOI:10.1109/TCOMM.2016.2533498 ( 0) 0)
|
| [10] |
WAND Jiadong, COURTADE T, SHANKAR H, et al. Soft information for LDPC decoding in flash: mutual-information optimized quantization[C]//Proceedings of 2011 IEEE Global Telecommunications Conference. Kathmandu, Nepal, 2011: 1−6.
( 0) 0)
|
| [11] |
WANG Jiadong, VAKILINIA K, CHEN T Y, et al. Enhanced precision through multiple reads for LDPC decoding in flash memories[J]. IEEE journal on selected areas in communications, 2014, 32(5): 880-891. DOI:10.1109/JSAC.2014.140508 ( 0) 0)
|
| [12] |
DONG Guiqiang, XIE Ningde, ZHANG Tong. Enabling NAND flash memory use soft-decision error correction codes at minimal read latency overhead[J]. IEEE transactions on circuits and systems I: regular papers, 2013, 60(9): 2412-2421. DOI:10.1109/TCSI.2013.2244361 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


