高光谱遥感是用数十至数百个连续且细分的光谱波段对地物持续遥感成像的技术。随着高光谱遥感技术的不断发展和成熟,高光谱遥感技术在军事侦查,矿产勘探侦测,农业、林业病虫害监测,渔业、畜牧业养殖等方面都取得了很大突破[1]。高光谱遥感具有波段多、获得的数据量大、相邻波段间相关性强的特点,导致数据之间冗余量大,从而给高光谱遥感图像分类带来了很大的困难[2]。基于这些难点,国内外学者就如何快速、准确地对高光谱遥感图像地物目标分类进行了一系列的研究[3−5]。常用的高光谱遥感图像分类按照对于地物分类时是否需要训练样本,可以大致分为无监督分类[6]、监督分类[7]与半监督分类[8]。对于无监督分类,其优点为不需要标记与训练。这使得无监督分类在对于数据处理上比较快速。但是由于高光谱数据波段间相关性强,只进行无监督分类,会造成高光谱数据所含大量信息未被完全使用,分类效果并不理想。而监督分类需要的标记训练样本较多,并且标记过程繁琐、耗时,成本昂贵[9]。针对此类问题,半监督分类在已知类别标记的训练样本不足的情况下,将未知类别的样本引入训练过程,自动地利用未标记样本提升分类性能[10]。
就分类器而言,支持向量机(support vector machine,SVM)[11]是基于统计学习理论的基础上于1995年提出的,其效果得到广泛好评。SVM的核心思想是把样本通过非线性映射方式将其投影到高维特征空间,以结构风险最小化原理为其原则,在高维特征空间中构造一个最优分类超平面。最小二乘孪生支持向量机算法(least squares twin support vector machines,LSTSVM)[12]是在SVM的基础上发展起来的分类工具,打破SVM类别边界平行分布的限制,寻找2个不平行的分类超平面,并使用等式代替不等式,分类效果得到进一步提升。
高光谱图像维数高、数据计算量大,给后续的分类处理造成困难。针对此问题,本文提出了一种融合波段选择和半监督分类的分类算法GADE_LSTSVM,使用LSTSVM作为分类工具,并在分类前加入波段选择过程,减少样本冗余波段,从而能够更快地从无标记样本中选取信息量丰富的样本。该算法使用遗传算法(genetic algorithm,GA)全局搜索最优波段组合,再使用差分进化算法(differential evolution,DE)选取未标记样本内信息量丰富的样本添加标记。波段选择方法减少冗余波段,提高了无标记样本中信息量丰富的样本的选取速率;辅助差分进化算法选取出的信息量丰富的未标记样本放入训练样本集,进而提高整个算法的分类精度。
1 LSTSVM算法LSTSVM算法是在SVM的基础上找出2个相对较小且不相互平行的分类超平面,并使得每个超平面各与其中一类样本尽可能近,与另一类样本尽可能远。把2个凸优化问题转变为2个线性方程问题,降低算法复杂度,减少计算量:
| $\begin{array}{l}\left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_{{\theta _1}{r_1}} \dfrac{1}{2}{\left\| {K \left( {{{A}}, {{{C}}^{\rm{T}}}} \right){\theta _1} + {{{e}}_{{1}}}{r_1}} \right\|^2} + \dfrac{c}{2}{{\xi}} _2^T{{{\xi}} _2} \\ {\rm{s}}{\rm{.t}}{\rm{.}} - \left( {K \left( {{{B}}, {{{C}}^{\rm{T}}}} \right){\theta _1} + {{{e}}_{{2}}}{r_1}} \right) + {\xi _2} = {e_2} \\ \end{array} \right.\\ \left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_{{\theta _2}{r_2}} \dfrac{1}{2}{\left\| {K \left( {{{B}}, {{{C}}^{\rm{T}}}} \right){\theta _2} + {{{e}}_{{2}}}{r_2}} \right\|^2} + \dfrac{c}{2}{{\xi}} _1^{\rm{T}}{{{\xi}} _1} \\ {\rm{s}}{\rm{.t}}{\rm{.}} - \left( {K \left( {{{A}}, {{{C}}^{\rm{T}}}} \right){\theta _2} + {{{e}}_{{1}}}{r_2}} \right) + {\xi _1} = {{{e}}_{{1}}} \\ \end{array} \right. \end{array} $ |
式中:A为训练样本集内正样本集;B为训练样本集内负样本集;C为正样本与负样本的组合;
| $K{\rm{(}}x, y{\rm{) = exp[}} - {{{\rm{||}}x - y{\rm{|}}{{\rm{|}}^{\rm{2}}}} / {{\rm{2}}{{\rm{\sigma }}^{\rm{2}}}}}{\rm{]}}$ |
问题的解为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\theta _1}} \\ {{r_1}} \end{array}} \right] = - {\left( {{{{Q}}^{\rm{T}}}{{Q}} + \dfrac{1}{c}{{{P}}^{\rm{T}}}{{P}}} \right)^{ - 1}}{{{Q}}^{\rm{T}}}{{{e}}_{{2}}}\\ \left[ {\begin{array}{*{20}{c}} {{\theta _2}} \\ {{r_2}} \end{array}} \right] = - {\left( {{{{P}}^{\rm{T}}}{{P}} + \dfrac{1}{c}{{{Q}}^{\rm{T}}}{{Q}}} \right)^{ - 1}}{{{P}}^{\rm{T}}}{{{e}}_{{1}}} \end{array} $ |
式中:
在本文所提GADE_LSTSVM算法中,首先利用遗传算法从高光谱图像的全部波段中优选出信息量丰富的波段,然后再使用差分进化算法将用于训练的无标记样本中信息量丰富样本筛选出来,最终与用于训练的有标记样本集相结合,使用LSTSVM进行训练。
由于高光谱图像的已标记样本数量较少,所以在高光谱图像分类中,需要将无标记信息利用起来。因为高光谱图像所含波段较多,使用全部波段来选取信息量丰富的无标记样本所需时间较长,且易造成过拟合现象。所以我们需要去除冗余信息,将信息量丰富的波段选出并加以应用。为了有效利用无标记样本信息,本文采用差分进化算法对来自无标记样本的有价值样本进行过滤,以扩充有限的带标签样本集,构造具有代表性的训练集,极大减少人工标记的成本。
遗传进化与差分进化都是启发式随机搜索算法,并且原理简单易于操作,容易求得全局最优解。经过波段选择后,差分进化算法再利用LSTSVM算法进行分类,有效地解决了由于标签不足造成的欠拟合问题。因此,DE算法结合LSTSVM算法是本文算法的关键。
2.1 波段选择中的遗传算法遗传算法利用种群进化来搜索最优解,且具有全局收敛性[13]。在本算法中,处理高光谱数据主要分为五步。
1)编码
对于高光谱图像所含有的所有已剔除噪声的波段进行编码。对于高光谱图像来说,其所含有的波段数多,使用常规的二进制编码得到的编码位数会很大,之后再将这个编码进行遗传交叉变异的时候会十分复杂,对计算量造成影响。所以用四进制编码代替二进制编码对高光谱图像的波段进行编码,减少编码长度。将编码设为L位,并且将高光谱图像的每个波段与L位四进制数一一对应。
2)初始化
控制参数:设初始种群中共有m1个染色体,其上各有n1个基因(n1是L的整数倍);交叉、变异概率分别设为Pc、Pm;终止迭代次数设为N1。
初始种群:随机生成m1×n1位四进制数,每一行中从起始位置顺次L位即为一个单位,并对应高光谱中的一个波段。该L位四进制数转换成的十进制数即为高光谱图像的的波段序号。
3)适应度函数
因为Jeffries−Matusita(JM)距离可以得到各类别样本之间的可分离性,所以在对高光谱图像中的两类进行距离统计时能发挥很好的作用[14]。因此,将JM距离Jij作为使用遗传算法进行波段选择的适应度函数。计算高光谱图像各类样本间的平均JM距离
| $ {J_{ij}} = {\left[ {2 \times \left( {1 - {e^{ - {D_{ij}}}}} \right)} \right]^{\frac{1}{2}}} $ |
式中:
| $ \begin{aligned} {D_{ij}} = & \dfrac{1}{2}\ln \dfrac{{\left| {\dfrac{1}{2}\left( {{{\mathop {{a}}\limits^ \circ }_i} + {{\mathop {{a}}\limits^ \circ }_j}} \right)} \right|}}{{\sqrt {\left| {{{\mathop {{a}}\limits^ \circ }_i}} \right|} }\sqrt {\left| {{{\mathop {{a}}\limits^ \circ }_j}} \right|} } + \\ & \dfrac{1}{8}{\left( {{{{\mu }}_i} - {{{\mu }}_j}} \right)^T}{\left( {\dfrac{{{{\mathop {{a}}\limits^ \circ }_i} + {{\mathop {{a}}\limits^ \circ }_j}}}{2}} \right)^{ - 1}}\left( {{{{\mu }}_i} - {{{\mu }}_j}} \right) \end{aligned} $ |
平均JM距离
| $ {\bar J} = \displaystyle \sum\limits_{i = 1}^{s - 1} {\displaystyle \sum\limits_{j = i + 1}^s {{J_{ij}}} } $ |
式中s为类别数。
4)遗传算子操作
选择操作:分别求出种群中的每个个体的JM距离并进行对比,将JM距离大的波段保留,并复制到下一代。
交叉、变异操作:以一定概率(Pm),从个体中随机选择用于交叉的基因,并再以一定的概率(Pc)实施变异。
5)终止条件
设置终止条件为最大迭代次数N1。最后,得到一个波段组合成的矩阵M。
2.2 结合差分进化算法的样本选取与遗传算法不同的是,差分进化算法根据父代个体间的差分矢量进行编译、交叉、选择操作[15−16]。
在本算法中所选高光谱波段数D即为问题维数,经过G次迭代后第i个种群向量为
| $ {{{X}}_{i,G}} = \left[ {{x_{{{M}}(1),i,G}},{x_{{{M}}(2),i,G}}, \cdots ,{x_{{{M}}(D),i,G}}} \right] $ |
式中:
基本变异方式的基本方程为:
| $ {{{V}}_{i,G}}{\rm{ = }}{{{X}}_{r_{1,G}^i}} + F \times \left( {{{{X}}_{r_{2,G}^i}} - {{{X}}_{r_{3,G}^i}}} \right) $ | (1) |
式中:
由式(1)可以看出差分进化算法中差分变异的基本方式。将种群中的某一个体叠加经缩放后另外2个的差分向量。为了使变异更加多样,本文算法将2个个体缩放因子F、λ加入到差分操作中,对式(1)加以改进得到:
| $ \begin{array}{l} {{{V}}_{i,G}}{\rm{ = }}{{{X}}_{i,G}} + F \times \left( {{{{X}}_{r_{2,G}^i}} - {{{X}}_{i,G}}} \right) + \lambda \times \left( {{{{X}}_{r_{2,G}^i}} - {{{X}}_{r_{3,G}^i}}} \right) \end{array} $ |
式中
与遗传算法的交叉变异有所不同,差分进化算法的交叉操作是通过在种群内随机选择个体来进行的。
| $ {u_{j,i,G}} = \left\{ \begin{array}{l} {v_{j,i,G}},\;{\rm{rand}}{_{i,j}}[0,1] \leqslant C_r \;\; {\rm{or}}\;j = {j_{{\rm{rand}}}}\\ {x_{j,i,G}},\;\;{\text{其他}} \end{array} \right. $ |
式中:
在本算法中将经过差分变异与交叉操作后的向量
| $ {u_{j,i,G}} = \left\{ {\begin{array}{*{20}{l}} {{{{U}}_{i,G}},\quad f\left( {{{{U}}_{i,G}}} \right) \leqslant f\left( {{{{X}}_{i,G}}} \right)}\\ {{{{X}}_{i,G}},\quad f\left( {{{{U}}_{i,G}}} \right) < f\left( {{{{X}}_{i,G}}} \right)} \end{array}} \right. $ |
式中
对于高光谱图像的多分类问题,由于SVM是一个二分类器,所以常通过组合的形式将其加以应用。应用的方法主要有一对多和一对一两种策略。本算法中LSTSVM属于SVM的改进算法,所以也通过一对多将之转化为多个二分类问题。
2.3 算法流程给定有标记样本集
1)使用遗传算法从高光谱图像的所有波段中选取出信息量较为丰富的20个波段参与训练;
2)选取有标记样本集
3)利用差分进化算法从
4)对
5)利用已经训练好的LSTSVM分类器开始对测试样本进行标记,测评该分类器的分类精度。
3 实验部分 3.1 实验数据为验证算法有效性,本文选取2个高光谱图像数据,分别是Indian pines数据集和Pavia大学数据集,从中选取8个主要类别参与分类实验。2个数据集的地物图如图1所示。为了更好地进行比较,2个高光谱图像的大小均设为144×144,其中,Indian pines原始数据集包含总波段数为200个,Pavia大学原始数据集包含125个波段,去除噪声后的波段数为103。

|
Download:
|
| 图 1 监督信息 | |
Indian pines数据集中地物的分布比较规则,每类地物的分布整体性好;而Pavia大学数据集中的同类地物分布较为分散,涉及区域较大。
3.2 实验仿真本实验中用于仿真的电脑其处理器为Intel(R)Core(TM)i7−4720HQ,RAM大小为8 GB,采用64位的windows10系统作为操作系统,具体用于仿真的软件为matlab2018a。
将总体分类精度(overall accuracy,OA)、平均分类精度(average accuracy,AA)、Kappa系数作为评价高光谱图像分类精度的准则。
设N是样本总数,mii是第i类正确分类的样本数,Ai为第i类的分类精度。
总体分类精度的值OA为:
| ${O_A} = \frac{1}{N}\sum\limits_{i = 1}^n {{m_{ii}}} $ |
第i类分类精度为:
| $ A_{i}=\frac{m_{i i}}{N_{i}} $ |
平均分类精度的值为AA:
| $ {A_A} = \frac{1}{N}\sum\limits_{i = 1}^n {{A_i}} $ |
Kappa系数:
| $ K = \frac{{N \times \displaystyle \sum\limits_{i = 1}^n {{m_{ii}}} - \displaystyle \sum\limits_{i = 1}^n {{N_i}} \times {m_{ii}}}}{{{N^2} - \displaystyle \sum\limits_{i = 1}^n {{N_i}} \times {m_{ii}}}} $ |
在实验中,遗传进化设置的参数为NP=20、四进制染色体编码长度为L=4、最大进化代数N1=200、交叉概率Pc=0.75、变异概率Pm=0.01。同理,差分进化算法的参数为NP=20、F=0.5、λ=0.5、Cr=0.8。并将LSTSVM作为基分类器,设置LSTSVM的核函数为高斯核函数,其惩罚因子C、核参数σ通过交叉验证法从
通过实验对比标准SVM、DE_LSTSVM、SVM_MS(SVM_margin sampling)和本文算法4种分类算法的优劣。实验随机选取10%的样本作为训练样本,其中10个为已标记样本,其他为无标记样本;其余90%的样本作为测试样本。首先对Indian pines数据集高光谱图像进行分类。表1给出了AA、OA、Kappa系数以及运行时间。
|
|
表 1 Indian pines高光谱图像分类精度 |
从表1可以看出DE_LSTSVM算法与SVM_MS算法的分类性能明显好于SVM。与DE_LSTSVM算法相比,本文的GADE_LSTSVM算法分类速度提升了62.742 0 s,而分类精度只有略微降低。与SVM_MS算法相比,本文算法在分类精度上有明显提高,OA提高了5.91%,AA提高了4.76%,Kappa提高了0.069 6。GADE_LSTSVM算法通过GA算法进行波段选择,DE算法又对信息量丰富的无标记样本进行筛选引入到已标记的训练样本集中,明显提高了分类速度。图2为4种算法分类结果的灰度图表示。

|
Download:
|
| 图 2 Indian pines数据集高光谱图像4种算法的分类结果 | |
我们可以观察出图2(b)、(c)、(d)的错分样本数量与图2(a)有明显差别。由图可知,本文算法以损失小部分分类精度为代价,使高光谱图像的分类速度有了显著提高。
用Pavia大学数据集高光谱图像再次验证。选取10%的样本作为训练样本,其中10个为已标记样本,其他为无标记样本;其余90%的样本作为测试样本。表2记录了4种算法的仿真结果,从表2可以看出本文所提出的算法比DE_LSTSVM算法的分类速度提高了26.442 0 s,而分类精度基本一致;比SVM_MS算法OA提高了7.24%,AA提高了3.99%,Kappa系数提高了0.092 4。
|
|
表 2 Pavia大学高光谱图像分类精度 |
标准SVM、DE_LSTSVM算法、SVM_MS算法和本文算法的仿真结果灰度图如图3所示。

|
Download:
|
| 图 3 Pavia大学数据集高光谱图像4种算法的分类结果 | |
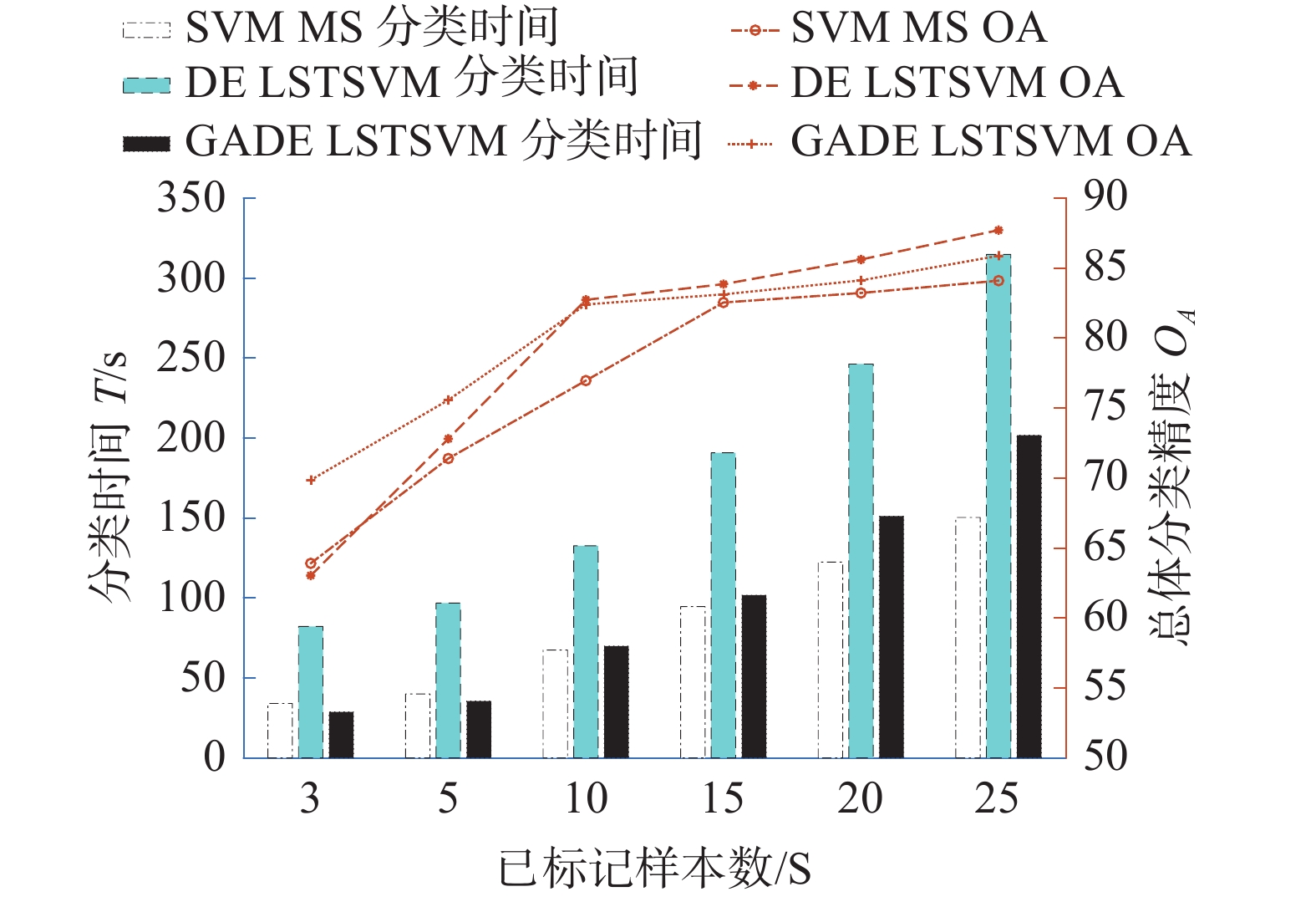
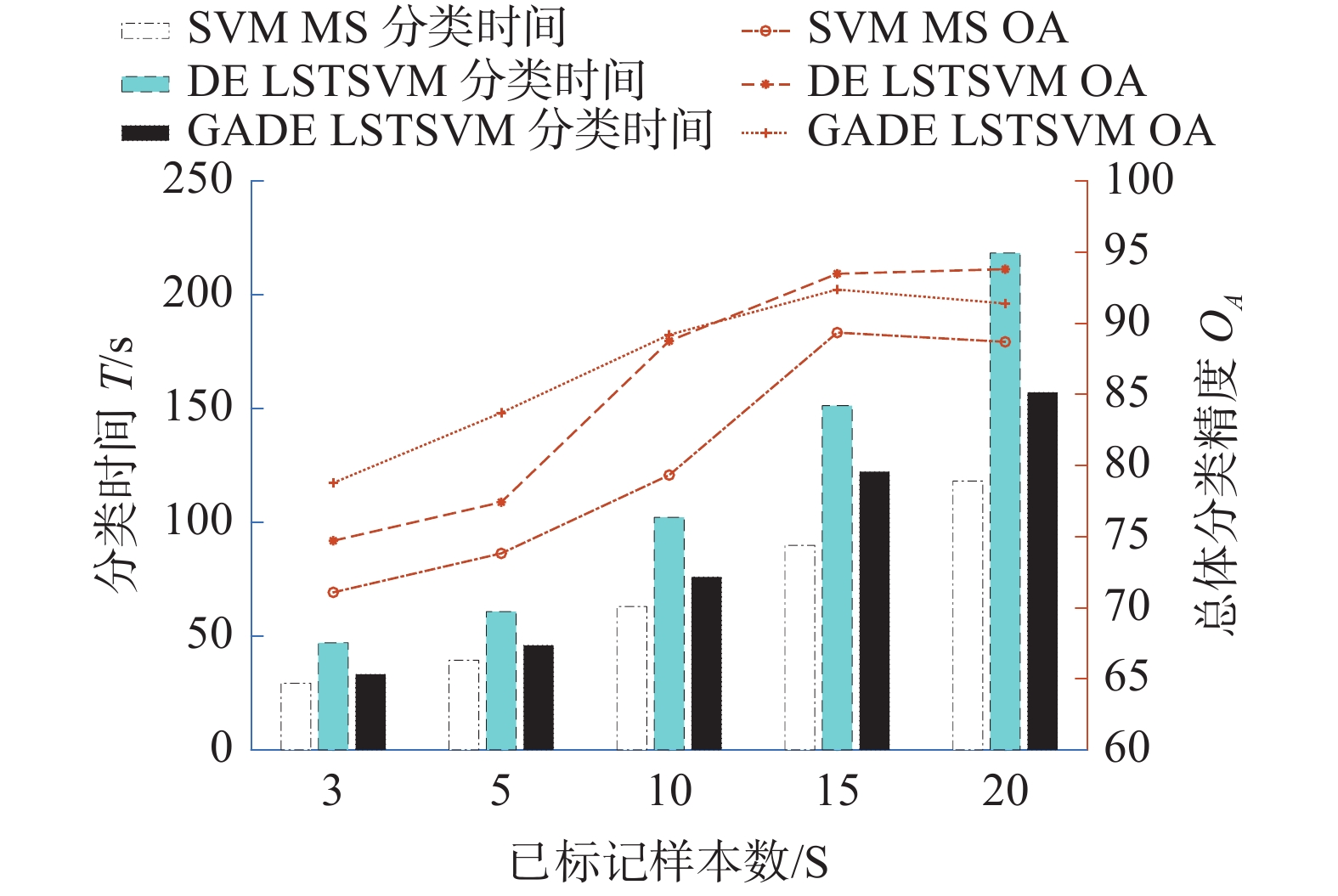
此外为了更直观地展现用于训练的带标签样本数目s与总体分类精度和分类速度之间的关系,图4、5将代表精度的折线图与代表速度的柱状图相结合进行对比。带标签样本数目s取3、5、10、15、20、25。从曲线图部分可以看出,本文所提算法在样本数目很少的情况下分类精度的优势更为明显。从柱状图部分可以看出,本文所提算法具有明显的分类速度优势。
|
Download:
|
| 图 4 带标签样本数与OA的关系曲线(Indian pines数据集高光谱图像) | |
|
Download:
|
| 图 5 带标签样本数与OA的关系曲线(Pavia大学数据集高光谱图像) | |
1)本文算法在分类之前进行波段选择,有效地减少有标签样本中的冗余信息对学习过程造成的计算量。
2)在带标记样本少的情况下,本文算法能够快速地选取信息量丰富的无标签样本扩充入训练样本集中,有效地提升了分类器的性能。
3)本文算法在已标记样本数量较少时优势十分明显。
今后的研究工作可以集中在尝试利用已标记样本的空间信息提高对小样本数据分类性能的改善方面。
| [1] |
童庆禧, 张兵, 郑兰芬. 高光谱遥感[M]. 北京: 高等教育出版社, 2006.
( 0) 0)
|
| [2] |
朱艳, 刘晓莉, 杨哲海. 高光谱数据的降维及Tabu搜索算法的应用[J]. 测绘科学技术学报, 2007, 24(1): 22-25, 29. DOI:10.3969/j.issn.1673-6338.2007.01.007 ( 0) 0)
|
| [3] |
ZHONG Yanfei, MA Ailong, ONG Y S, et al. Computational intelligence in optical remote sensing image processing[J]. Applied soft computing, 2018, 64: 75-93. DOI:10.1016/j.asoc.2017.11.045 ( 0) 0)
|
| [4] |
CHENG Gong, HAN Junwei. A survey on object detection in optical remote sensing images[J]. ISPRS journal of photogrammetry and remote sensing, 2016, 117: 11-28. DOI:10.1016/j.isprsjprs.2016.03.014 ( 0) 0)
|
| [5] |
杜培军, 夏俊士, 薛朝辉, 等. 高光谱遥感影像分类研究进展[J]. 遥感学报, 2016, 20(2): 236-256. ( 0) 0)
|
| [6] |
WANG Jianyu, XUE Yongqi, RONG Shu, et al. Airborne hyperspectral and infrared remote sensing technology and application[C]//Proceedings of 2006 Joint 31st International Conference on Infrared Millimeter Waves and 14th International Conference on Teraherz Electronics. Shanghai, China, 2006.
( 0) 0)
|
| [7] |
HUNG C C, KULKARNI S, KUO B C. A new weighted fuzzy c-means clustering algorithm for remotely sensed image classification[J]. IEEE journal of selected topics in signal processing, 2011, 5(3): 543-553. DOI:10.1109/JSTSP.2010.2096797 ( 0) 0)
|
| [8] |
VILLA A, BENEDIKTSSON J A, CHANUSSOT J, et al. Hyperspectral image classification with independent component discriminant analysis[J]. IEEE transactions on geoscience and remote sensing, 2011, 49(12): 4865-4876. DOI:10.1109/TGRS.2011.2153861 ( 0) 0)
|
| [9] |
周千琪. 基于稀疏表示和半监督主动学习的小样本高光谱数据分类问题研究[D]. 银川: 北方民族大学, 2016.
( 0) 0)
|
| [10] |
高飞, 朱福利. 基于样本类别确定度的半监督分类[J]. 北京航空航天大学学报, 2018, 44(9): 1941-1951. ( 0) 0)
|
| [11] |
CORTES C, VAPNIK V. Support vector networks[J]. Machine learning, 1995, 20(3): 273-297. ( 0) 0)
|
| [12] |
KUMAR M A, GOPAL M. Least squares twin support vector machines for pattern classification[J]. Expert systems with applications, 2009, 36(4): 7535-7543. DOI:10.1016/j.eswa.2008.09.066 ( 0) 0)
|
| [13] |
陈国良, 王煦法, 庄镇泉, 等. 遗传算法及其应用[M]. 北京: 人民邮电出版社, 1996.
( 0) 0)
|
| [14] |
张明阳. 基于进化优化学习的高光谱特征选择与提取[D]. 西安: 西安电子科技大学, 2018.
( 0) 0)
|
| [15] |
STORN R, PRICE K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 ( 0) 0)
|
| [16] |
刘明广. 差异演化算法及其改进[J]. 系统工程, 2005, 23(2): 108-111. DOI:10.3969/j.issn.1009-6744.2005.02.018 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


