随着电子技术的不断发展,信息化战争已经逐渐成为了信息时代的基本战争形态[1]。在信息化战争中,雷达的作战对象、工作环境和工作任务都发生了极大的变化,传统雷达在现代化战争中所面对的挑战越来越大,也推动了雷达向着智能化的方向不断发展。2006年,认知雷达的概念被提出,认知雷达对于环境的适应程度较高,被认为将在现代战场中扮演极其重要的作用[2]。
在认知雷达的概念被提出之后,国内外的专家便开始了对于认知雷达的研究。目前,对于认知雷达的研究多是聚焦在认知雷达的关键技术的研究,其中研究最多的是波形自适应设计技术。目前在波形自适应设计技术研究中常用的5种方法,分别是模糊函数法、特征值法、最大化各类目标之间的距离的方法、动态规划法、信息论法[3]。以上的方法各有优劣,但是随着各种智能化算法的提出以及发展,也为我们对于波形自适应设计技术的研究指明了方向[4−5]。
本文针对于信杂比限定下的最大互信息雷达波形设计模型进行研究。该模型作为一种非线性优化模型,通常对于该模型的求解算法采用序列二次规划算法(SQP算法)。但序列二次规划算法在对模型的求解过程中,其求解效果会受到寻优起始值的影响,并且在算法的迭代求解过程中,极易陷入局部最优,算法的全局性极差。本文在求解该模型时,在序列二次规划算法中引入了粒子群算法,将粒子群算法与序列二次规划算法结合,充分发挥粒子群算法的全局性和序列二次规划算法局部寻优精确的特性,对模型进行求解,来提升序列二次规划算法对目标模型的求解效果。
1 信杂比限定下的最大互信息雷达波形设计模型采用信息论法的自适应波形设计技术中,较为基础的方法是基于最大互信息准则[6]和最大信杂比准则[7]来进行波形自适应设计。根据雷达检测理论和信息论的相关知识,分别对于最大互信息准则和最大信杂比准则的求解模型和求解结果进行了研究。
最大互信息准则的波形自适应设计是在雷达发射波形的能量限制下,使得目标和回波之间的互信息最大,即要求解的模型为:
| $\left\{ \begin{array}{l} I(y(t);x(t)/s(t)) = \\ \;\;\;\;\;\;\;\;\;T\int\limits_w {{\rm{ln}}(1 + \dfrac{{2{{\left| {S(f)} \right|}^2}\sigma _G^2(f)}}{{2{{\left| {S(f)} \right|}^2}\sigma _c^2(f) + {P_n}(f)T}})} {\rm{d}}f, f \in \omega \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\int\limits_w {{{\left| {S(f)} \right|}^2}{\rm{d}}f = 2{\text{π}}E,} f \in \omega \end{array} \right.$ |
式中:
利用拉格朗日乘子法对该模型进行求解,得到的雷达发射波形为:
| $ {\left| {S(f)} \right|^2} = \max [0,C(f)(A - D(f))] $ |
式中:
| $A = T/\lambda $ |
| $C(f) = {{\sigma _g^2} / {(2\sigma _c^2T + \sigma _g^2)}}$ |
| $D(f) = {{T\sigma _c^2(f)} / {2\sigma _G^2(f)}}$ |
最大信杂比准则则是在雷达发射波形的能量限制下,使得雷达接收到的回波信杂比最大,其目标方程为:
| $\left\{ \begin{array}{l} \max {d_{{\rm{SNR}}}} = \int\limits_w {\dfrac{{2{{\left| {S(f)} \right|}^2}\sigma _g^2}}{{\sigma _n^2 + 2{{\left| {S(f)} \right|}^2}\sigma _c^2}}{\rm{d}}f,} {\rm{ }}f \in \omega \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\rm{ }}\int\limits_w {{{\left| {S(f)} \right|}^2}{\rm{d}}f = 2{\text{π}}E,} f \in \omega \end{array} \right.$ |
同理,利用拉格朗日乘子法对该模型进行求解,得到的雷达发射波形为:
| $ {\left| {S(f)} \right|^2} = \max [0,\dfrac{{\sigma _g^2\sqrt {\dfrac{{\sigma _n^2}}{{2\lambda }} - \dfrac{{\sigma _n^2}}{2}} }}{{\sigma _c^2}}] $ |
在现实的雷达工作中,雷达为了能够准确地发现目标,雷达接收系统接收到的雷达回波信杂比需要满足一定的要求。当接收到的雷达回波的值低于一个门限值,则认为雷达无法探测到该目标,该门限值即为雷达的信杂比限定。将最大互信息准则和最大信杂比准则相联系,设置信杂比限定为S0,设置本文求解的模型为信杂比限定下的最大互信息雷达波形设计模型为:
| $ \left\{ \begin{array}{l} \max T\int\limits_w {\ln (1 + \;\dfrac{{2{{\left| {S(f)} \right|}^2}\sigma _g^2}}{{T[\sigma _n^2 + 2{{\left| {S(f)} \right|}^2}\sigma _c^2]}}){\rm{d}}f \geqslant {d_{{\rm{SN}}{{\rm{R}}_0}}}} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\;\int\limits_w {\dfrac{{2{{\left| {S(f)} \right|}^2}\sigma _g^2}}{{\sigma _n^2 + 2{{\left| {S(f)} \right|}^2}\sigma _c^2}}{\rm{d}}f \geqslant {d_{{\rm{SN}}{{\rm{R}}_0}}}} \\ \;\;\;\; \;\,\,{\rm{ }}\int\limits_w {{{\left| {S(f)} \right|}^2}{\rm{d}}f = 2{\text{π}}E} \\ \end{array} \right. $ | (1) |
该目标方程式中所要求解的目标函数是目标和回波之间的互信息,雷达的发射能量和接收到的回波信杂比是2个限制条件。本模型即是要在2个限制条件下求解雷达波形,使得目标与回波间的最大互信息量最大。
2 基于序列二次规划算法的自适应波形优化算法要求解的信杂比限定下的最大互信息雷达波形设计模型作为一种非线性优化模型,序列二次规划算法是最为常用的求解该类问题的方法。
序列二次规划算法的主要思想是:在算法的整个迭代过程中,利用二次规划子问题来对目标方程的下降方向进行求解,结合价值函数对每一步的求解步长进行求解,并对预期得到的目标矩阵进行更新,求得所要求解问题的最优解[8]。在序列二次规划算法的整个计算过程之中,核心的步骤就是对预期求解的波形优化模型的下降方向dk进行求解。即将式(1)中的目标函数与限定函数进行求导,形成二次规划子问题[9]:
| $ \left\{ \begin{array}{l} \min \dfrac{1}{2}{({{{d}}_k})^{\rm{T}}}{{{H}}_k}{{{d}}_k} + \Delta f{({{{x}}_k})^{\rm{T}}}{{{d}}_k} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\Delta {h_i}{({{{x}}_k})^{\rm{T}}}{{{d}}_k} + {h_i}({{{x}}_k}) = 0 \\ \;\; \;\;\;\Delta {g_i}{({{{x}}_k})^{\rm{T}}}{{{d}}_k} + {g_i}({{{x}}_k}) \geqslant 0 \\ \end{array} \right. $ | (2) |
通过式(2)可以对波形优化模型的下降方向dk及拉格朗日乘子进行求解。整体的求解步骤如下:首先将求解得到的dk作为波形优化模型的下降方向;然后利用价值函数来确定每一步迭代的步长,并且利用价值函数和Armijo准则来确定波形优化模型的步长;最后利用迭代公式来确定迭代点。在所有的步骤结束后,利用修正的BFGS公式对Hessian矩阵进行修正[7]。
利用序列二次规划算法对目标求解的信杂比限定下的最大互信息雷达波形设计模型的计算步骤如下[10]:
1)设置迭代的初始值;
2)将模型转化为二次规划子问题,得到求解的模型的下降方向dk;
3)判断当前点是否满足以下2个条件:
| $ {\left\| {{{{d}}_k}} \right\|_1} \leqslant {\varepsilon _1} $ | (3) |
| $ \sum\limits_{i \in E} {\left| {{h_i}(x)} \right|} + \sum\limits_{i \in E} {\max \left\{ {0, - {g_i}(x)} \right\}} \leqslant {\varepsilon _2} $ | (4) |
若满足式(3)、(4)2个条件,则停止仿真,此时的解为求解方程得到的最优解;
4)利用价值函数以及Armijo准则对求解波形优化模型迭代的步长进行计算和确定;
5)利用Armijo准则,对使式(5)成立的最小非负整数进行求解和计算:
| $ \phi ({{{x}}_k} + {\rho ^m}{{{d}}_k},{\sigma _k}) - \phi ({{{x}}_k},{\sigma _k}) \leqslant \eta {\rho ^m}\phi ({{{x}}_k},{\sigma _k}){{{d}}_k} $ | (5) |
并对波形优化模型的迭代点进行更新:
| $ {{{x}}_{k + 1}} = {{{x}}_k} + {\rho ^m}{{{d}}_k} $ |
6)利用最小二乘乘子更新算法中的相应参数;
7)用BFGS对Hessian矩阵进行修正;
8)持续迭代,直至迭代停止。
3 粒子群序列二次规划算法粒子群算法的计算过程如下[11]:
1)对算法参数进行初始化,包括种群规模的大小、预期解的维数、算法的最大迭代次数;
2)设置解的可行域,在可行域范围内,对迭代开始时各个粒子的运动范围和运动速度进行设置;
3)对每个粒子的历史最优函数值和群体最优位置进行初始化;
4)迭代开始,根据式(6)、(7)更新算法中每个粒子的速度和位置:
| $ v_{id}^{t + 1} = v_{id}^t + {c_1}{r_1}(p_{id}^t - x_{id}^t) + {c_2}{r_2}(p_{gd}^{} - x_{id}^t) $ | (6) |
| $ x_{id}^{t + 1} = v_{id}^{t + 1} + x_{id}^t $ | (7) |
5)持续迭代,实时计算每个粒子的适应度值,针对于本文来讲,即求式(1)中的目标函数;
6)根据粒子的函数值更新每个粒子和整个群体的最优位置信息;
7)若当前的迭代次数等于最大迭代次数,则算法结束;否则算法转向步骤4),继续进行迭代。
粒子群序列二次规划算法将序列二次规划算法作为一个局部寻优的过程,将粒子群算法作为全局寻优的部分,在迭代时,将粒子群算法在计算中粒子得到的全局最优位置作为序列二次规划算法的初始点,并进行完整的序列二次规划算法的局部搜索求解。若序列二次规划算法得到的解优于粒子群算法的全局最优解,则将序列二次算法得到的解直接作为全局最优解进行下一轮迭代;若序列二次规划的解并不优于粒子群算法的全局最优解,则不对粒子群寻优得到的全局最优解进行修改。该算法将粒子群算法与序列二次规划算法有机结合起来,发挥了粒子群算法的全局搜索能力和序列二次算法的求解精度能力。算法的工作流程如图1所示。

|
Download:
|
| 图 1 粒子群序列二次规划算法流程 | |
为了对算法结果有更加准确的对比,首先使用序列二次规划算法对目标模型进行求解;在相同的仿真条件下,再使用本文提出的粒子群序列二次规划算法进行模型求解并比较仿真结果。
4.1 仿真参数设置仿真时,设置目标与目标间的距离是10 km,雷达的带宽
| ${w_f} = [{f_c} - w/2,{f_c} + w/2] = [0.995 \;{\rm{GHz}},1.005 \;{\rm{GHz}}]$ |
设置目标脉冲响应
| $\sigma _G^2(f) = B\exp [ - \alpha {(f - {f_c})^2}]$ |
式中:
| $B = 7.957 7 \times {10^{ - 16}}$ |
假设噪声为高斯白噪声,而且只是热噪声,温度为
| $\sigma _n^2(f) = k{T_s} = 1.381 \times {10^{ - 23}} \;{\rm{J/K}} \times 300\; {\rm{K}} = 4.143\;0 \times {10^{ - 21}} \;{\rm{J}}$ |
设置最小可检测信杂比S0为5 dB、发射功率为1 W、序列二次规划算法最大迭代次数为1 000次、粒子群序列二次规划算法的最大迭代次数为2 000次,在发射波形长度为
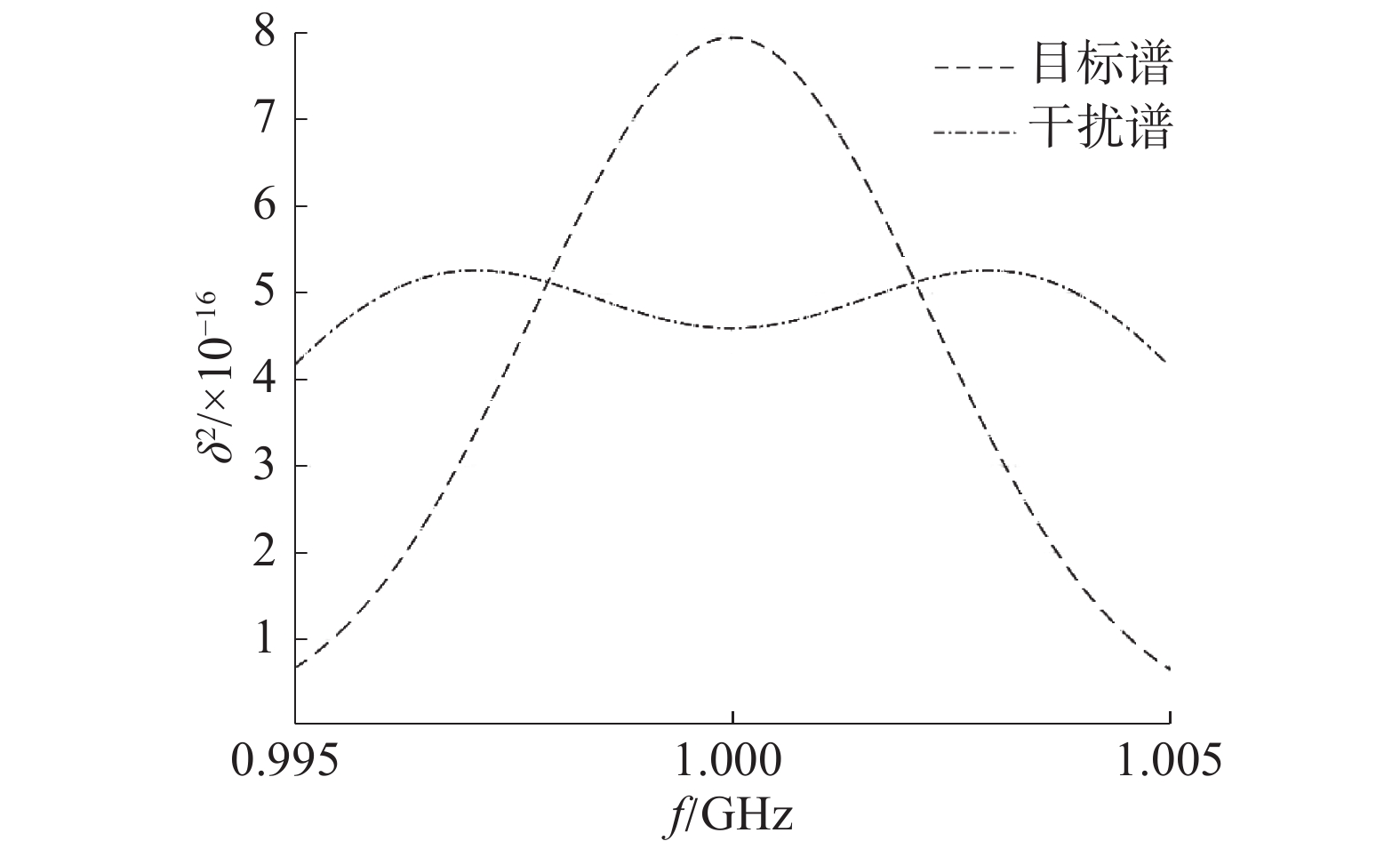
传统的仿真验证中,目标谱和干扰谱的分布如图2所示。本文为了便于验证算法性能,在保证目标谱分布不变时,将干扰谱进行随机调整,得到如图3所示的目标谱及干扰谱分布。
|
Download:
|
| 图 2 目标谱和干扰谱分布情况1 | |

|
Download:
|
| 图 3 目标谱和干扰谱分布情况2 | |
采用序列二次规划算法对模型进行求解,在如图2所示的干扰谱和目标谱分布情况下,得到在不同的寻优起始点时最优波形的设计结果如图4所示。

|
Download:
|
| 图 4 序列二次规划算法在图2情况下求解结果 | |
以上3个仿真过程,迭代次数和每次实验得到的最大互信息量如表1所示。
|
|
表 1 图4中3个仿真过程最大互信息量及迭代次数 |
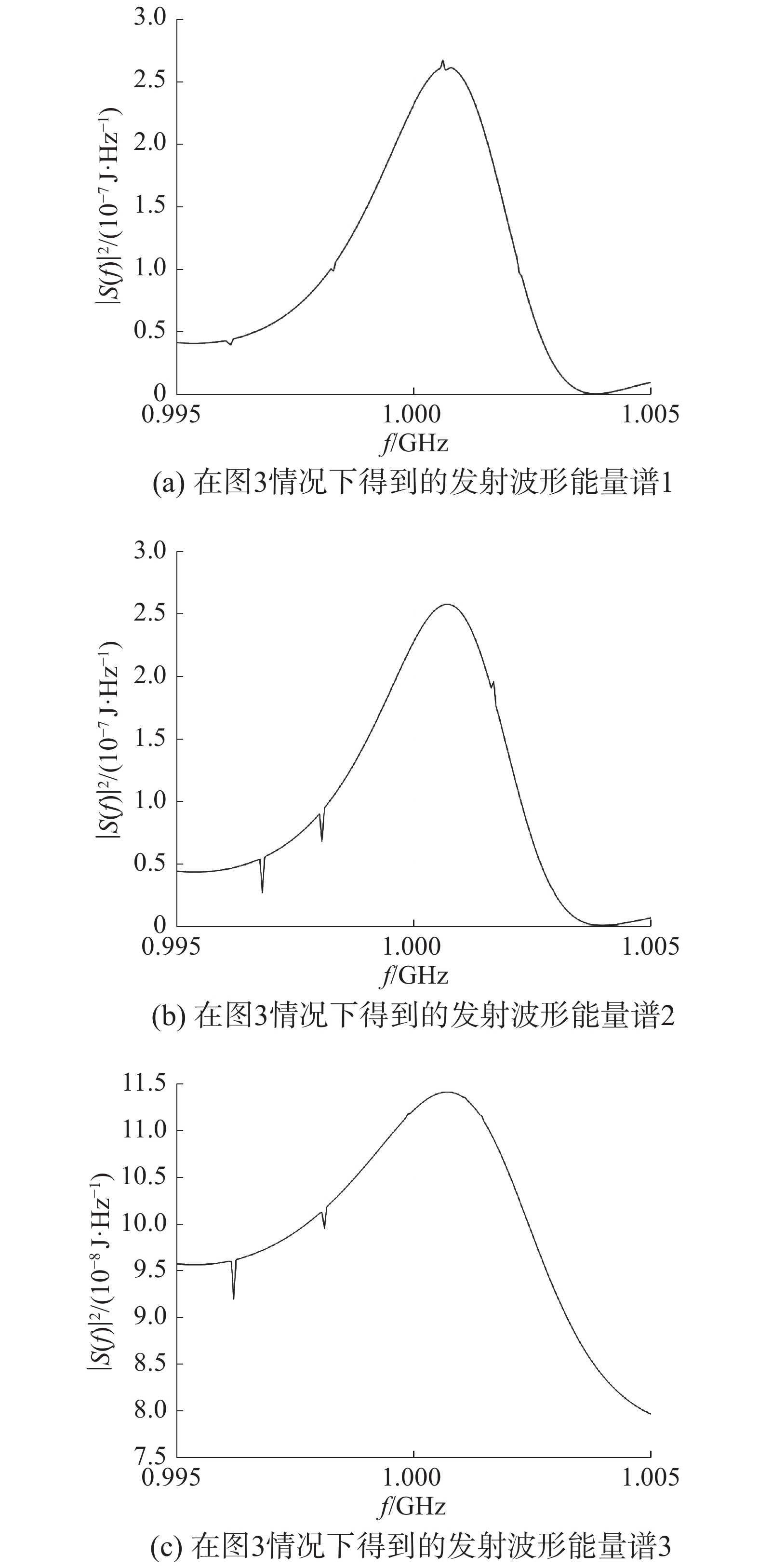
在如图3所示的干扰谱和目标谱分布情况下,得到的在不同的寻优起始点时得到的最优波形设计结果如图5所示。以上3个仿真过程,迭代次数和得到的最大互信息量如表2所示。
|
Download:
|
| 图 5 序列二次规划算法在图3情况下求解结果 | |
|
|
表 2 图5中3个仿真过程最大互信息量及迭代次数 |
通过以上结果可以得出,序列二次规划算法能够实现对优化模型进行求解。但是在求解过程中,需要人为设置寻优起始点,寻优初始值设定的不同,对算法的结果存在很大的影响。同时算法在运算过程中存在较为明显的局部收敛现象,算法极易陷入局部最优。
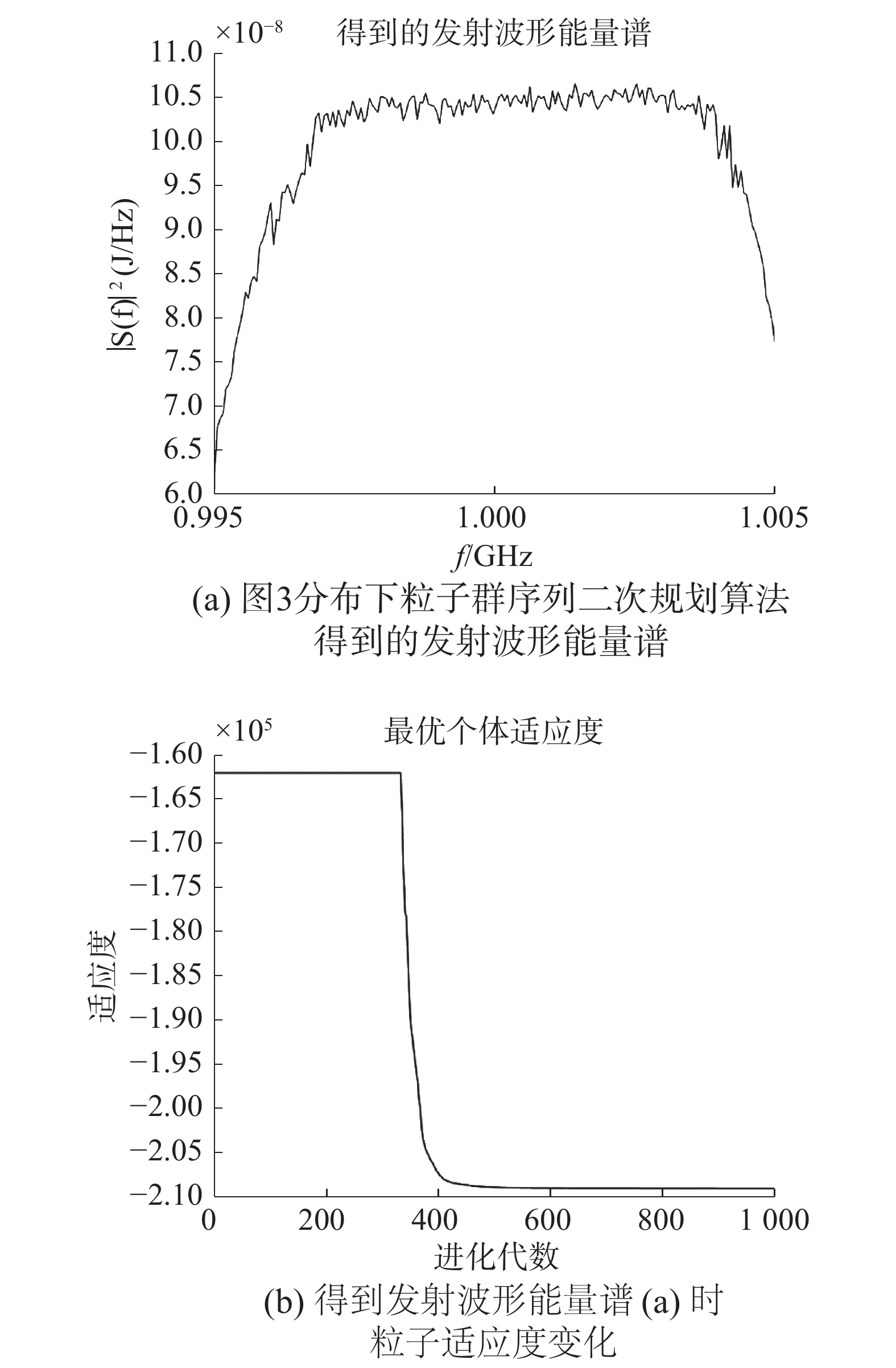
4.3 粒子群序列二次规划算法仿真结果在粒子群序列二次规划算法对于模型的求解过程中,仿真过程所采用的参数与4.2节中一致,采用粒子群的大小为1 000。同样,在相同的目标谱和干扰谱情况下,分别进行3次实验,分别记录这3次实验得到的最大互信息量和算法收敛时的迭代次数。同时,分别采用粒子群算法和遗传算法对模型进行求解和算法的对比。使用粒子群序列二次规划算法对目标模型求解结果的部分仿真图如图6、7所示,在不同目标谱和干扰谱分布情况下各个算法对目标模型的求解结果如表3、4所示。

|
Download:
|
| 图 6 粒子群序列二次规划算法在图2分布下对目标模型部分求解结果 | |
|
Download:
|
| 图 7 粒子群序列二次规划算法在图3分布下对目标模型部分求解结果 | |
|
|
表 3 各算法在图2分布下得到的波形最大互信息量和迭代次数 |
|
|
表 4 各算法在图3分布下得到的波形最大互信息量和迭代次数 |
通过图4~7与表1~4中数据可以看出,粒子群序列二次算法在解决信杂比限定下的最大互信息雷达波形设计问题的研究中,有效地提升了传统序列二次规划算法、粒子群算法和遗传算法在解决该问题时的收敛速度和得到的最优波形的最大互信息量,有效地避免了传统序列二次规划算法依赖寻优起始点和易陷入局部最优的问题,提高了算法的全局性。
5 结论本文针对于序列二次规划算法在计算信杂比限定下的最大互信息雷达波形设计模型中,求解结果易受到寻优初始值的影响、同时易陷入局部最优的问题,在算法中引入了粒子群算法作为全局寻优算法,将序列二次规划算法作为局部寻优算法,形成了粒子群序列二次规划算法,并利用该算法对模型进行求解,通过仿真结果可以看出:
1)粒子群序列二次规划算法因为初始值是随机设定的,避免了因人为设定寻优初始值导致的计算结果的差别;
2)粒子群序列二次规划算法在得到最优解时的迭代次数与序列二次规划算法相比,有明显的提升;
3)粒子群序列二次规划算法对模型求解后得到的最优波形的最大互信息量与序列二次规划算法、粒子群算法、遗传算法相比,有明显提升;
4)本文设计的算法,虽然增大了波形设计求解模型的精度,但增大了求解模型所需要的时间消耗,降低了问题处理的实时性。
| [1] |
徐艳国, 李国刚, 倪国新. 雷达系统未来发展趋势探析[J]. 中国电子科学研究院学报, 2013, 8(5): 474-480. DOI:10.3969/j.issn.1673-5692.2013.05.008 ( 0) 0)
|
| [2] |
HAYKIN S. Cognitive radar: a way of the future[J]. IEEE signal processing magazine, 2006, 23(1): 30-40. DOI:10.1109/MSP.2006.1593335 ( 0) 0)
|
| [3] |
王彬. 认知雷达波形优化设计研究[D]. 沈阳: 东北大学, 2011.
( 0) 0)
|
| [4] |
GUI R R H, WANG Wenqin. Constant modulus waveforms with restraining spectral interferences for cognitive MIMO radar[C]//Proceedings of 2017 IEEE Radar Conference (RadarConf). Seattle, USA: IEEE, 2017: 335−339.
( 0) 0)
|
| [5] |
WANG Li, ZHANG Yunlei, LIAO Qingmin, et al. Robust waveform design for multi-target detection in cognitive MIMO radar[C]//Proceedings of 2018 IEEE Radar Conference (RadarConf18). Oklahoma City, USA: IEEE, 2018: 116−120.
( 0) 0)
|
| [6] |
曹伟. 认知雷达的波形设计算法研究[D]. 成都: 电子科技大学, 2011.
( 0) 0)
|
| [7] |
牛建栋. MIMO认知雷达波形设计与实现[D]. 西安: 西安电子科技大学, 2013.
( 0) 0)
|
| [8] |
鞠默然, 李新波, 石要武. 基于信噪杂比最大能量分配认知雷达波形设计[J]. 吉林大学学报(信息科学版), 2015, 33(3): 230-234. DOI:10.3969/j.issn.1671-5896.2015.03.002 ( 0) 0)
|
| [9] |
李慧. 基于LFM信号的MIMO雷达发射波形设计方法研究[D]. 西安: 西安电子科技大学, 2017.
( 0) 0)
|
| [10] |
石国春. 关于序列二次规划(SQP)算法求解非线性规划问题的研究[D]. 兰州: 兰州大学, 2009.
( 0) 0)
|
| [11] |
张开伟. 基于改进粒子群优化算法的船舶推力分配研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


