带隙基准源广泛用于各种模拟集成电路上,其精度以及稳定性直接影响到整体电路的性能,因此高精度以及高稳定性的带隙基准源对于提高整体电路的性能必不可少。传统的带隙基准结构[1-3]在理论上可以达到很高的精度以及稳定性,但是在实际运用中由于工艺的差异会导致元件失配,从而影响基准的精度[4],而且随着工作时间的增加,元件之间的失配也会逐渐变大[5],造成的结果就是基准的稳定性随着时间的增加越来越差。器件的失配严重影响了基准的精度以及稳定性。针对该问题,本文设计了一款全新结构的电压基准源,该基准源充分使用动态元件匹配技术,最大程度地减少了器件的失配。通过仿真表明,该电路能够非常好地改善由于器件失配而造成的精度以及稳定性的恶化。
1 基准源的工作原理带隙基准的基本原理是正负温度系数抵消,从而减小基准电压随温度的变化。根据参考文献[1],三极管的基极−发射极电压
| $V = a{V_{{\rm{be}}}} + b\Delta {V_{{\rm{be}}}}$ | (1) |
如果式(1)对温度的偏导为0,该式产生的电压V就是基准电压。
图1为传统的带隙基准电压源电路,QP1与QP2为PNP三极管,前者发射极面积为后者的m倍;OTA为运算放大器,其输出Vref的计算公式为:
| $ V_{{\rm{ref}}}=V_{{\rm{b e}} _1}+I_{1}\left(R_{1}+R_{2}\right)+\left(I_{1}+I_{2}\right) R_{4} $ | (2) |
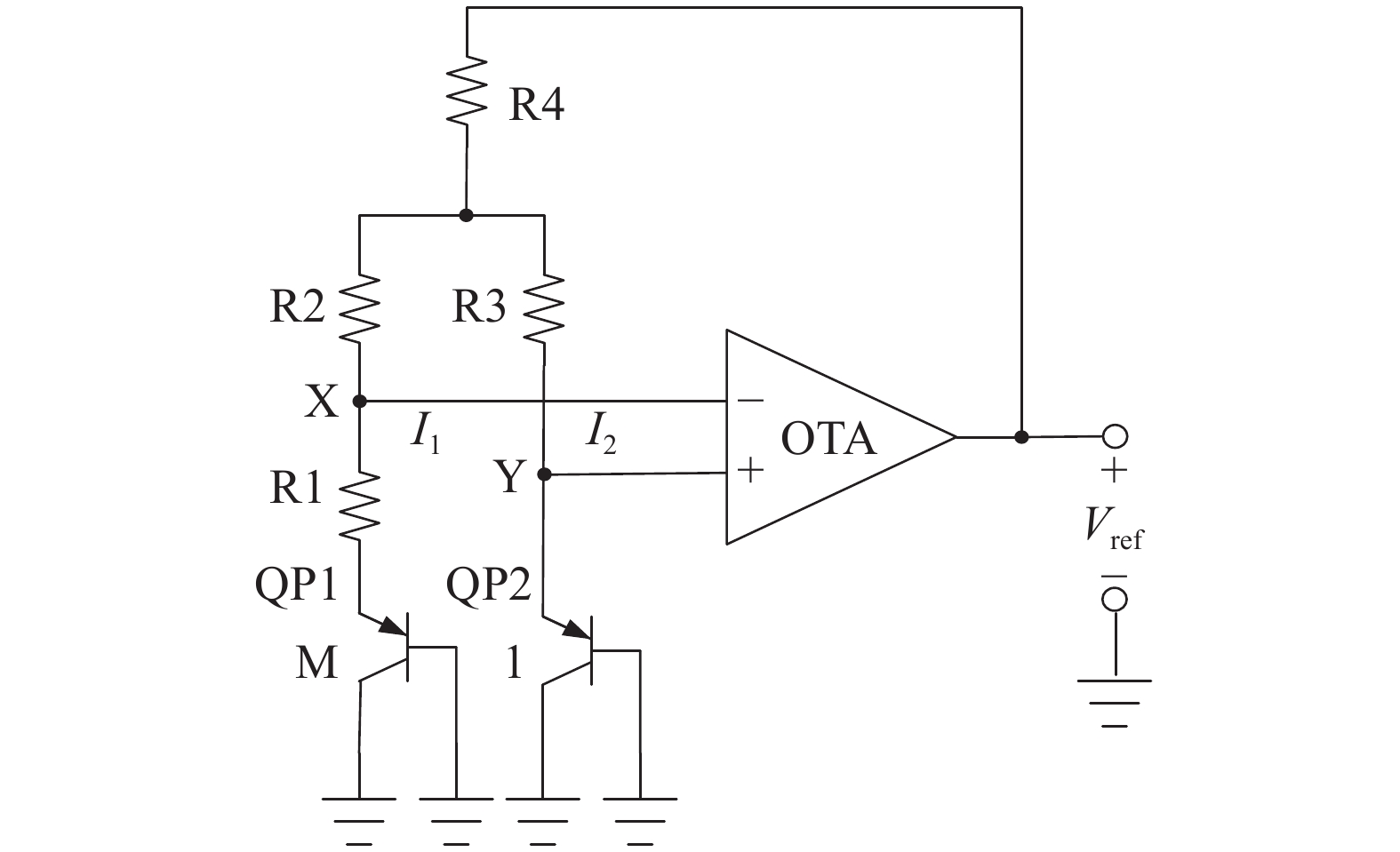
|
Download:
|
| 图 1 传统带隙基准电路 | |
由参考文献[6],运算放大器OTA的作用为:
| $V_X = V_Y$ | (3) |
所以:
| $I_1 = I_2 = \frac{{{V_{{\rm{be}}_2}} - {V_{{\rm{be_1}}}}}}{{R_1}} = \frac{{\Delta {V_{{\rm{be}}}}}}{{R_1}}$ |
由参考文献[1],可以得到
| ${V_{{\rm{be}}}} = {V_T}\ln \frac{I}{{m{I_S}}}$ |
| $\Delta {V_{{\rm{be}}}} = {V_T}\ln m$ |
所以,式(2)可以写成:
| $V_{\rm{ref}} = {V_{{\rm{be1}}}} + {V_T}\frac{{(R_1 + R_2 + 2R_4)}}{{R_1}}\ln m$ | (7) |
式(4)与式(1)具有相同的结构,式(4)对温度T求导,并令求导结果为0,则有:
| $ \frac{\partial V_{{\rm{ref}}}}{\partial T}=\frac{\partial V_{{\rm{b e}}_ 1}}{\partial T}+\frac{\partial V_{T}}{\partial T} \frac{\left(R_{1}+R_{2}+2 R_{4}\right)}{R_{1}} \ln m=0 $ | (8) |
由式(5)可以看出,只要选择合适的m、R1、R2、R4,就可以得到与温度无关的基准电压。
式(3)是得到基准电压的核心条件,为保证该式成立,必须使用高增益、器件高度匹配的理想运算放大器。在实际运用中,高增益可以通过多级放大器实现,但是器件高度匹配对电路的结构以及器件的一致性要求非常高,这也是本文主要解决的问题。
2 电路设计与实现图2为本文提出的电路原理图,该电路由3部分组成,A为基准核心部分,B为运算放大器,C为输出电压稳定电路。该电路的偏置电流Ibias由单独的启动电路提供。

|
Download:
|
| 图 2 本文提出的带隙基准电路 | |
根据工作原理分析,结合图2的A部分,可以得出该基准的输出电压计算公式为:
| $V_{\rm{ref}} = {V_{{\rm{be_1}}}} + {V_T}\frac{{(R_1 + R_2 + 2R_4)}}{{R_1}}\ln m$ |
B部分为运算放大器,为两级放大,第一级B1为普通的双输入双输出的共源差分电路,其增益为:
| ${A_{{V_1}}} = {g_{{m_7}}}{R_5}$ |
式中
第二级B2为折叠共源共栅差分放大器[7],其增益为:
| ${A_{{V_2}}} = {g_{{m_{12}}}}{r_{{o_{12}}}}{g_{{m_{10}}}}{r_{{o_{10}}}}$ | (11) |
式中:
总的增益为两级增益的乘积,能够符合理想放大器高增益的特点。
B3为共漏结构的缓冲器,能够减少运算放大器的功耗以及噪声。
C部分为电压稳定电路,通过负反馈减少由于输入电压的变化带来对输出基准电压的影响。
B部分性能的好坏直接影响到式(3)能否成立,该部分性能指标是增益以及器件匹配程度,前面的分析已经得出该放大器具有大的增益,所以最大的影响来源于器件的匹配程度。
2.2 电路元件失配分析在2.1节已经分析得出,从增益的角度来讲,该基准运算放大器可以看作是理想的,因此影响运放性能的主要因素是器件的失配。由于运放由差分电路组成,对差分电路来说,器件的失配主要是差分电路两路器件的失配造成的,这些失配为:
1)B1中MP7与MP8、R5与R6的失配;
2)B2中MP9与MP10、MN3与MN4的失配;
3)B2中MP4、MP11组成的支路与MP5、MP12组成的支路的失配。
对失配造成的影响进行分析,B1中MP7与MP8、R5与R6的失配:假设MP7与MP8的输入电压相等,由于MP7与MP8的失配使流过MP7与MP8的电流产生差异,设差异量为ΔI;假设R5与R6的失配量为ΔR,则由此造成的输出电压失配量为ΔV=ΔIΔR;其他失配造成的影响与上述分析相似。
可以看出,如果可以消除这些器件之间失配,就能很好地保证运放为理想的。
2.3 动态元件匹配动态元件匹配技术是为了保证差分电路支路信号相等。图3为动态元件匹配等效结构框图,

|
Download:
|
| 图 3 动态元件匹配等效结构 | |
控制信号使用n相不交叠时钟来实现[8],在时钟为高电平时开关开启,低电平时关断。假设每个输入对应的开关开启时间为
| $\left[ \begin{gathered} {o_1} \\ {o_2} \\ \vdots \\ {o_n} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{p_{11}}}&{{p_{12}}}& \ldots &{{p_{1n}}} \\ {{p_{21}}}&{{p_{22}}}& \ldots &{{p_{2n}}} \\ \vdots & & & \vdots \\ {{p_{n1}}}&{{p_{n2}}}& \ldots &{{p_{nn}}} \end{array}} \right]\left[ \begin{gathered} {t_1}{i_1} \\ {t_2}{i_2} \\ \vdots \\ {t_n}{i_n} \\ \end{gathered} \right]$ | (12) |
式中
如果了解某一输入的误差大小,则可以赋予该输入特定的权重[9-11],这样可以自主地控制误差的比重。在实际运用中,相同工艺的器件失配率都是一样的,所以采用随机概率,这样在一段时间后概率都相等,为1/n,所以,式(7)可以表示为:
| $\left[ \begin{gathered} {o_1} \\ {o_2} \\ \vdots \\ {o_n} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{n}}&{\dfrac{1}{n}}& \ldots &{\dfrac{1}{n}} \\ {\dfrac{1}{n}}&{\dfrac{1}{n}}& \ldots &{\dfrac{1}{n}} \\ \vdots & & & \vdots \\ {\dfrac{1}{n}}&{\dfrac{1}{n}}& \ldots &{\dfrac{1}{n}} \end{array}} \right]\left[ \begin{gathered} {t_1}{i_1} \\ {t_2}{i_2} \\ \vdots \\ {t_n}{i_n} \\ \end{gathered} \right]$ | (13) |
可以得到各个支路的输出都相等:
| ${o_i} = \frac{1}{n}\displaystyle\sum\limits_{j = 1}^n {{t_j}{i_j}} $ |
保证了每条支路的信号都相等,这样就消除了由于器件失配带来的误差。
图2中,DEM1、DEM2、DEM3为动态元件匹配电路[7],分别用来解决2.2节所提出的3个失配。可以看出它由2个时钟控制,可以得出在本设计中n=2,时钟为2相不交叠时钟。具体的DEM电路及控制时钟如图4、5所示,各开关的开启时间相等设为t。将这些参数带入式(8),可以得出2条支路的输出电压表达式为:
| $\left[ {\begin{array}{*{20}{c}} {{V_{{{o_1}}}}} \\ {{V_{{{o_2}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2}}&{\dfrac{1}{2}} \\ {\dfrac{1}{2}}&{\dfrac{1}{2}} \end{array}} \right]\left[ \begin{gathered} {V_{i_1}}t \\ {V_{i_2}}t \\ \end{gathered} \right]$ |
可以得到输出的失配量为0,很好地解决了器件失配造成的输出失配。

|
Download:
|
| 图 4 动态元件匹配实现 | |

|
Download:
|
| 图 5 动态元件匹配时钟信号 | |
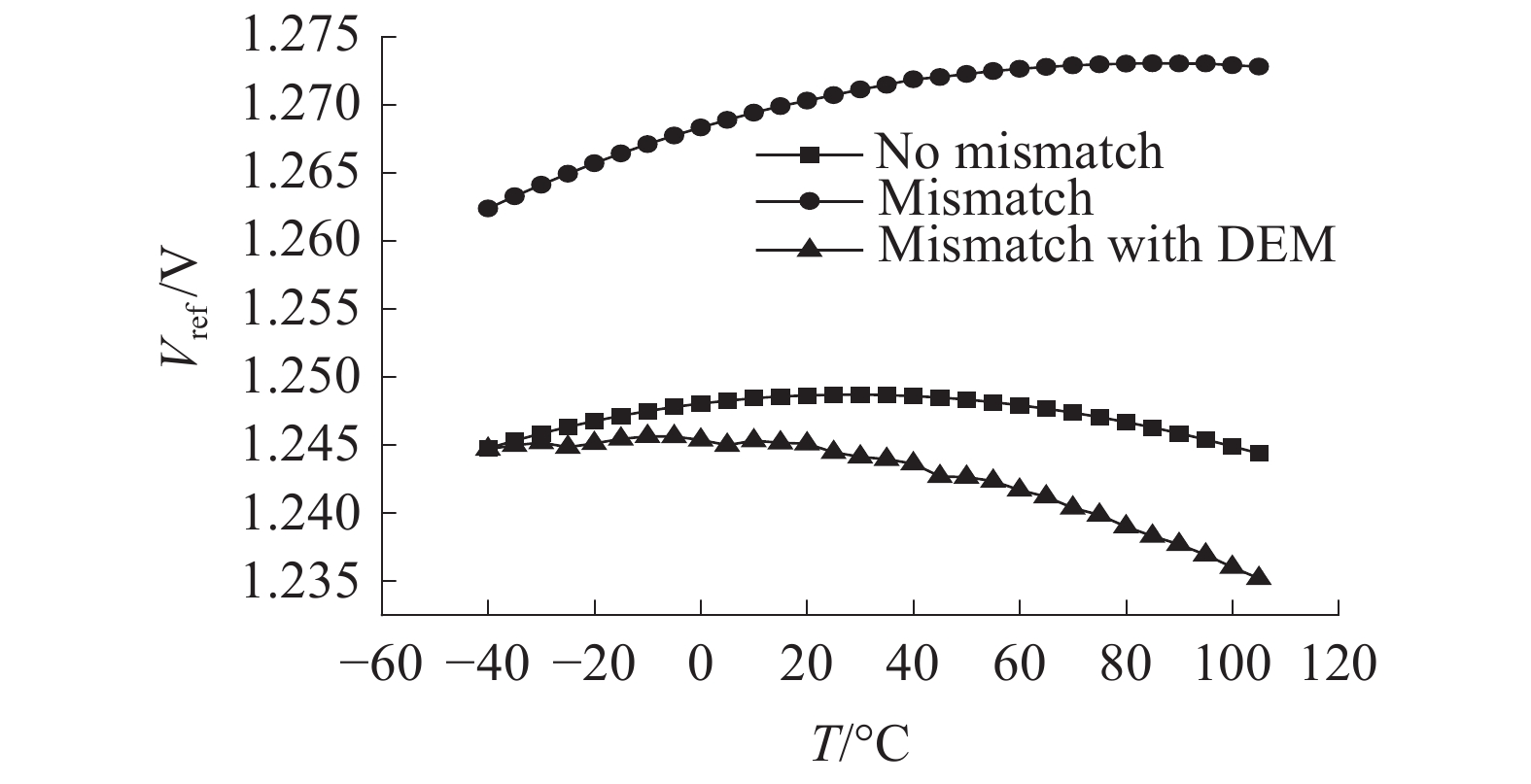
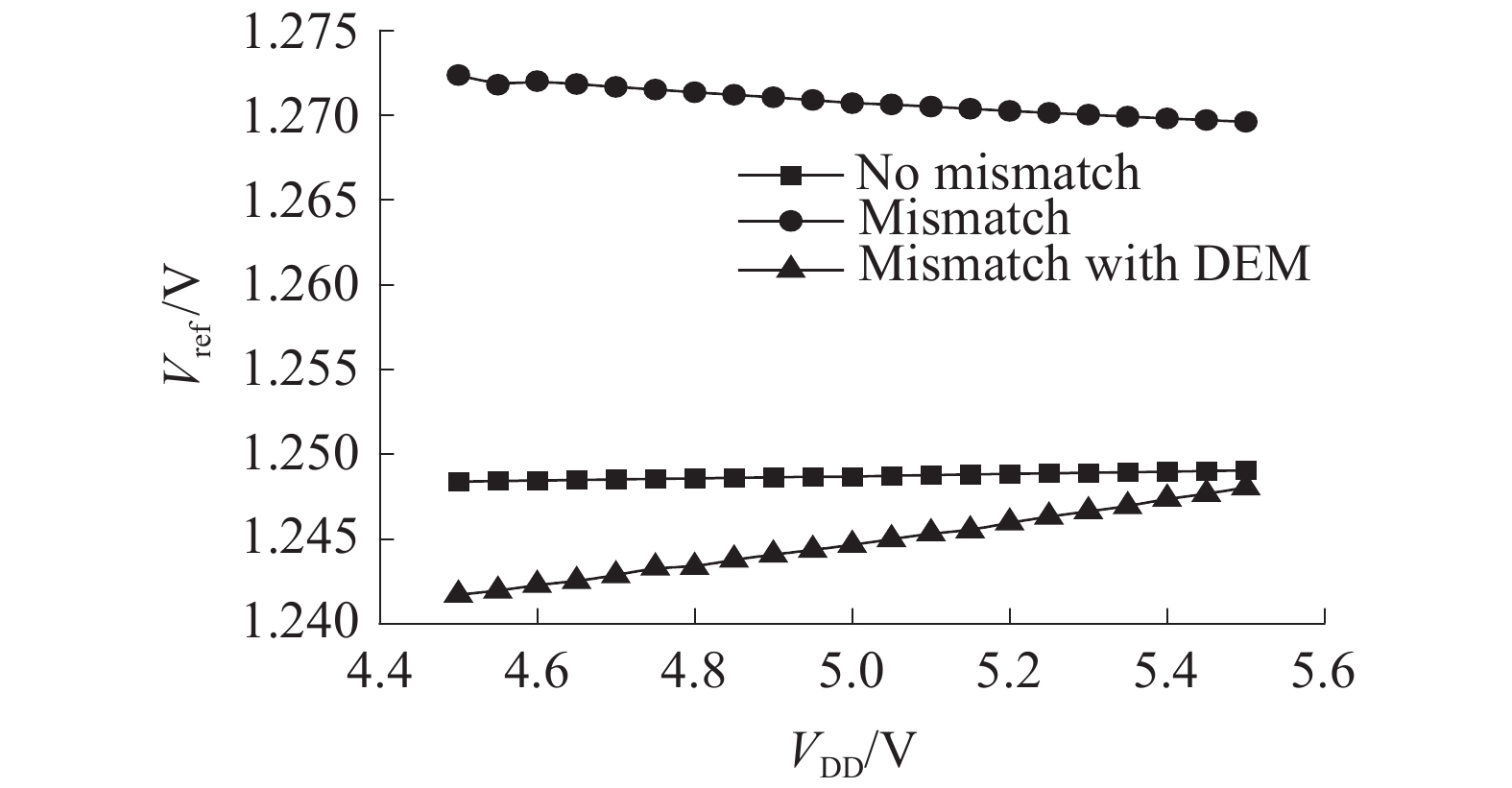
基于BICMOS 0.15 μm工艺,通过Cadence的spectre仿真软件对电路进行仿真。为了说明动态元件匹配技术对于器件失配的改善效果,需要仿真3种电路:加入失配、使用动态元件匹配技术电路(mismatch with DEM),加入失配、没有使用动态元件匹配技术电路(mismatch)以及没有加入失配、理想情况下电路(no mismatch)。分别仿真了这3种电路的温度特性、电压特性以及不同工艺角下的特性。仿真过程中加入失配的方法是对2.2节中提到的器件加入2%的失配[12]。
图6为3种电路在供电5 V、温度233~378 K(−40~105 ℃)条件下的
|
Download:
|
| 图 6 温度特性仿真结果对比 | |
图7为3种电路在温度为298 K(25 ℃)、供电电压为4.5~5.0 V条件下
|
Download:
|
| 图 7 电压特性仿真结果对比 | |
表1为在298 K(25 ℃)、电源电压5 V时,3种电路在不同工艺角情况下的
|
|
表 1 不同工艺角基准电压输出 |
提出了一款基于动态元件匹配技术的带隙基准,该基准能够很好地降低器件失配带来的误差,保证了
1)通过对电路的温度特性仿真表明,5.0 V供电、温度在233 K(−40 ℃)~378 K(105 ℃)变化时,相比于没有使用动态元件匹配的电路,该电路最少能够减小68%的误差;
2)通过对电路的电压特性仿真表明,25 ℃、电压在4.5~5.5 V变化时,相比于没有使用动态元件匹配的电路,该电路最少能够减小70%的误差;
3)在不同工艺角情况下,相比于没有使用动态元件匹配的电路,该电路最少能够减小68%的误差。
由于改善了器件失配造成的影响,可以得出该电路具有高稳定性。本论文只在一种工艺下进行了验证,在不同工艺下是否需要不同的考虑,这是以后需要研究的方向。
| [1] |
RAZAVI B. Design of analog CMOS integrated circuits[M]. 2nd ed. New York: McGraw-Hill Education, 2017: 301–324.
( 0) 0)
|
| [2] |
GRAY P R, HURST P J, LEWIS S H, et al. Analysis and design of analog integrated circuits[M]. 5th ed. New York: Wiley, 2009: 321–326.
( 0) 0)
|
| [3] |
廖陆威, 冯全源. 无源标签中的全MOS电压基准源[J]. 应用科技, 2018, 45(3): 35-38, 43. ( 0) 0)
|
| [4] |
秦少宏, 胡永贵, 胡云斌, 等. 一种高PSRR无电阻带隙基准源[J]. 微电子学, 2017, 47(4): 457-460. ( 0) 0)
|
| [5] |
刘帘曦, 杨银堂, 朱樟明. 基于MOSFET失配分析的低压高精度CMOS带隙基准源[J]. 西安电子科技大学学报(自然科学版), 2005, 32(3): 348-352. DOI:10.3969/j.issn.1001-2400.2005.03.005 ( 0) 0)
|
| [6] |
贺炜, 冯全源. 一种高温度性能的带隙基准源[J]. 电子器件, 2015, 38(1): 18-22. DOI:10.3969/j.issn.1005-9490.2015.01.005 ( 0) 0)
|
| [7] |
曹璐, 刘宏, 田彤. 一种采用数字修调技术的低温漂带隙基准设计[J]. 电子设计工程, 2017, 25(5): 150-153, 157. ( 0) 0)
|
| [8] |
佛朗哥·马洛贝蒂. 数据转换器[M]. 程军, 陈贵灿, 译. 西安: 西安交通大学出版社, 2013: 218.
( 0) 0)
|
| [9] |
VAN DE PLASSCHE R. Dynamic element matching for high-accuracy monolithic D/A converters[C]//Proceedings of IEEE International Solid-state Circuits Conference Digest of Technical Papers. Philadelphia, PA, USA, 1976: 148–149.
( 0) 0)
|
| [10] |
NYS O J A P, HENDERSON R K. An analysis of dynamic element matching techniques in sigma-delta modulation[C]//Proceedings of IEEE International Symposium on Circuits and Systems Circuits and Systems Connecting the World. Atlanta, GA, USA, 1996: 231–234.
( 0) 0)
|
| [11] |
HENDERSON R, NYS O J A P. Dynamic element matching techniques with arbitrary noise shaping function[C]//IEEE International Symposium on Circuits and Systems Circuits and Systems Connecting the World. Atlanta, GA, USA, 1996: 293–296.
( 0) 0)
|
| [12] |
杨晓春, 于奇, 宋文青, 等. 一种采用斩波调制的高精度带隙基准源的设计[J]. 微电子学与计算机, 2013, 30(1): 86-89. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


