温室植物的产量取决于温室内环境的温度、空气湿度等小气候要素的适宜度[1],尤其是较好的温度和气流分布,对于植物生长有着极其重要的作用。在所有环境因子中,适宜的温度是植物生长的首要条件,过低的温度甚至会造成温室内植物的死亡。因此,温室通风口的设置和风速都会对温室内气流的分布情况有较大的影响。程秀花等[1]提出室内气流的速度和分布情况较易受到植物的影响;汪郑邦[2]认为植物温室的气流分布对作物生长有较大的影响,不均匀的气流分布容易在作物周围形成换流,影响作物的蒸腾和光合作用;刘文合等[3]的研究表明通过对温室进行升温,可以使得温室内气温显著升高,但对温室内土壤深处的温度影响不大;周伟等[4]通过试验证明了通风口的设置和风速都会对温室内气流的分布情况有较大的影响,同时温室的气流分布对植物蒸腾和光合作用有较大的影响。因此,如何合理优化温室结构,得到适宜的风速和温度并使两者均匀性提高是当前急需解决的重要问题。
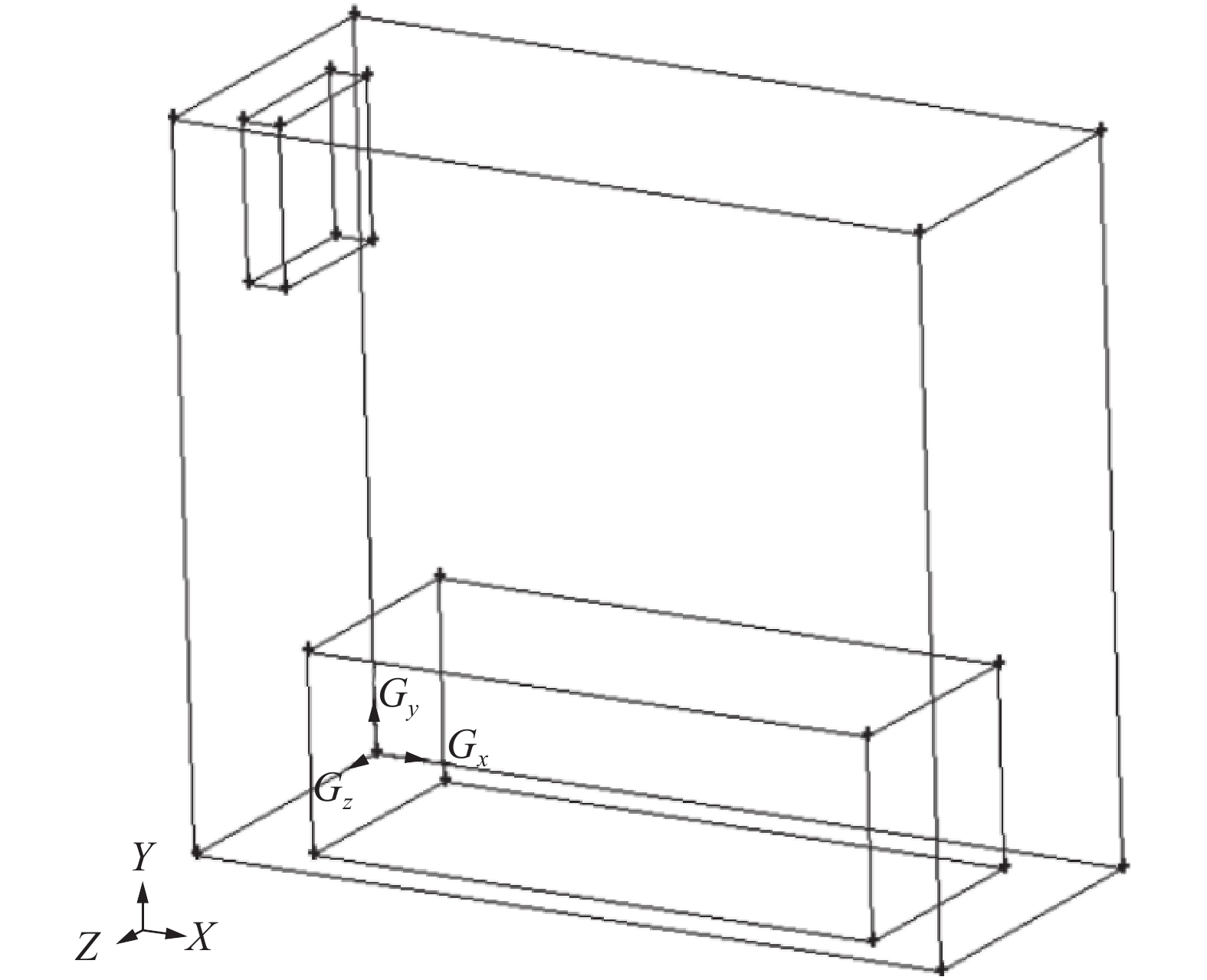
1 材料和方法 1.1 温室模型试验在东北林业大学进行,模拟温室建立在室内,受外界环境影响因素较小。温室的长×宽×高为2 m×0.83 m×1.8 m,由于温室是密闭的,因此忽略温室的门,并对温室四周及顶部进行简化,即将温室的顶部和四周均视为以浮法玻璃为材料。考虑到植物的冠层阻力,将植物模型简化为长1.50 m、宽0.6 m、高0.5 m的多孔介质,置于温室正中央。暖气扇规格为0.4 m×0.4 m,置于温室西侧,离地面1.3 m高处。采用Gambit进行以温室西北角为零点的温室模型的建立和网格化,得到的玻璃温室模型如图1所示。
|
Download:
|
| 图 1 玻璃温室模型 | |
在温室中选取Z=0.415 m处的截面,均匀分布6个监测点,高度分别为Y=0.6 m和1.2 m,将监测点依次记为

|
Download:
|
| 图 2 Z=0.415 m截面监测点布置(Y=0.6 m和Y=1.2 m) | |
|
Download:
|
| 图 3 Z=0.415 m截面监测点布置(X=1 m) | |
当Fluent模拟温室环境时,使用标准k−ε模型[5]将温室内的气流视为遵循质量守恒方程、动量守恒方程和能量守恒方程的湍流。
动量守恒方程指出,所有的流动在实际情况下都应该遵循动量守恒定律,定律用公式表示为:
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$ |
式中的u、v、w分别为在x、y、z方向上温室内气流流速的分量
动量守恒用公式表现为:
| $\begin{gathered} \frac{{\partial (\rho uu)}}{{\partial x}} + \frac{{\partial (\rho uv)}}{{\partial y}} + \frac{{\partial (\rho uw)}}{{\partial z}} = - \frac{{\partial P}}{{\partial x}} + \\ {\mu _{{\rm{eff}}}}\left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right) \\ \end{gathered} $ |
| $\begin{gathered} \frac{{\partial (\rho vu)}}{{\partial x}} + \frac{{\partial (\rho vv)}}{{\partial y}} + \frac{{\partial (\rho vw)}}{{\partial z}} = - \frac{{\partial P}}{{\partial y}} + \\ {\mu _{{\rm{eff}}}}\left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right){\rm{ - }}{\rho _{{\rm{ref}}}}g[1 - \beta (T - T{\rm{ref}})] \\ \end{gathered} $ |
| $\begin{gathered} \frac{{\partial (\rho wu)}}{{\partial x}} + \frac{{\partial (\rho wv)}}{{\partial y}} + \frac{{\partial (\rho ww)}}{{\partial z}} = - \frac{{\partial P}}{{\partial z}} + \\ {\mu _{{\rm{eff}}}}\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {y^2}}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) \\ \end{gathered} $ |
式中:
能量守恒用公式表示为
| $\begin{gathered} \frac{{\partial (\rho uT)}}{{\partial x}} + \frac{{\partial (\rho vT)}}{{\partial y}} + \frac{{\partial (\rho wT)}}{{\partial z}} = - \frac{q}{{{C_P}}} + \\ \frac{{{\lambda _{{\rm{eff}}}}}}{{{C_p}}} + \left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right) \\ \end{gathered} $ |
式中:
在处理封闭室内因温差引起的浮升力项时采用Boussinesq假设[7]。Boussinesq假设是对流体流动现象的一种简化,假设认为:流体中的黏性耗散忽略不计;除密度外其他物性为常数;对密度仅考虑动量方程中与体积力有关的项,其余各项中的密度亦作为常数。重力项中的密度如若采用作参考温度,则在不同温度
| $\rho {\rm{ = }}{\rho _{\rm{0}}}\left[ {{\rm{1 - }}\beta \left( {T - {T_0}} \right)} \right]$ |
式中:
流经多孔介质的空气可通过Darcy-Forchheimer理论描述为
| ${S_\varphi } = - \left( {\frac{\mu }{{{K_p}}} + \frac{{{C_F}}}{{\sqrt {{K_p}} }}\rho {u^2}} \right)$ |
式中:
将植物视为各向同性的多孔介质[9],并建立其与温室内部风速的数学关系模型:
| ${S_\varphi } = - {I_{{\rm{LAV}}}}{C_D}\rho {u^2}$ |
式中:
对于多孔介质动量源项,使用幂律模型,自定义经验系数
在使用Gambit划分网格时将整个玻璃温室作为计算域,采用非结构化四面体网格(混合TGrid网格类型以及Tet/Hybrid混合单元)将温室整体划分为四面体混合网格单元[10],并局部加密暖风扇出风口和植物区域,以适应气流和温度可能出现的较大变化[11]。
1.3.3 边界条件因为温室密闭性较好且置于室内,不考虑太阳辐射和漏风的影响,对模型进行简化。将暖风扇侧的边界条件设为速度入口条件,吹出水平方向25 ℃暖风,平均速度为1 m/s;覆盖层全部简化为玻璃,设为壁面条件,其与整个温室进行能量交换的方式主要为对流传热和传导[10],初始温度设为20 ℃;为简化能量交换过程,在进行模拟时不考虑其他的传热过程。将拥有大的热容量的土壤的边界条件设为壁面[12],初始温度设为20 ℃。
1.3.4 求解运算在进行模拟时,为修正速度,选用SIMPLEC算法:梯度项选用最小二乘法;压力项采用标准算法;能量和动量采用二阶迎风;为加快收敛速度,黏性和湍流选用一阶迎风。
2 FLUENT仿真结果与验证 2.1 FLUENT仿真结果用Fluent进行模拟的结果如图4、5所示。在吹入热风后,暖风口周围区域的气体流速变化明显,且存在较大梯度。气流从暖风扇水平送入温室后,略微向下方运动,在温室内部的东面、暖风扇正下方和温室底部形成涡流,且温度与风速有着直接的关系。

|
Download:
|
| 图 4 Y=0.5 m和Y=0.1 m处速度云图 | |

|
Download:
|
| 图 5 Y=0.5 m和Y=0.1 m处温度云图 | |
选取温室内植物冠层平面Y=0.5 m和植物内部平面Y=0.1 m的速度云图(图4)进行分析。当风速为0.30~1.00 m/s时,植物生长较好[13]。在使用Fluent进行模拟计算后,在距离地面0.5 m处的平均空气流速为0.152 m/s,最低速度为0.009 m/s,低于最佳风速;而植物冠层部分没有处于最适风速的区域出现。在平面Y=0.1 m处气流平均流速为0.195 m/s,最小流速为0.013 m/s,低于适宜风速的最小值0.3 m/s,最大风速为0.552 m/s,虽略大于0.3 m/s,但植物内部达到适宜植物生长的风速的部分仅占整体的20%。综上所述,此时的气体流动不适于植物的生长。
选取温室内植物表面Y=0.5 m和植物内部Y=0.1 m的温度云图(图5)进行分析。在暖风口附近温度最高,温度与其他区域相比有很大的梯度。在2个平面内最高温度可达24.45 ℃,平均温度23.17 ℃,温差的最大值为1.28 ℃,此温度较适于大部分植物的生长。
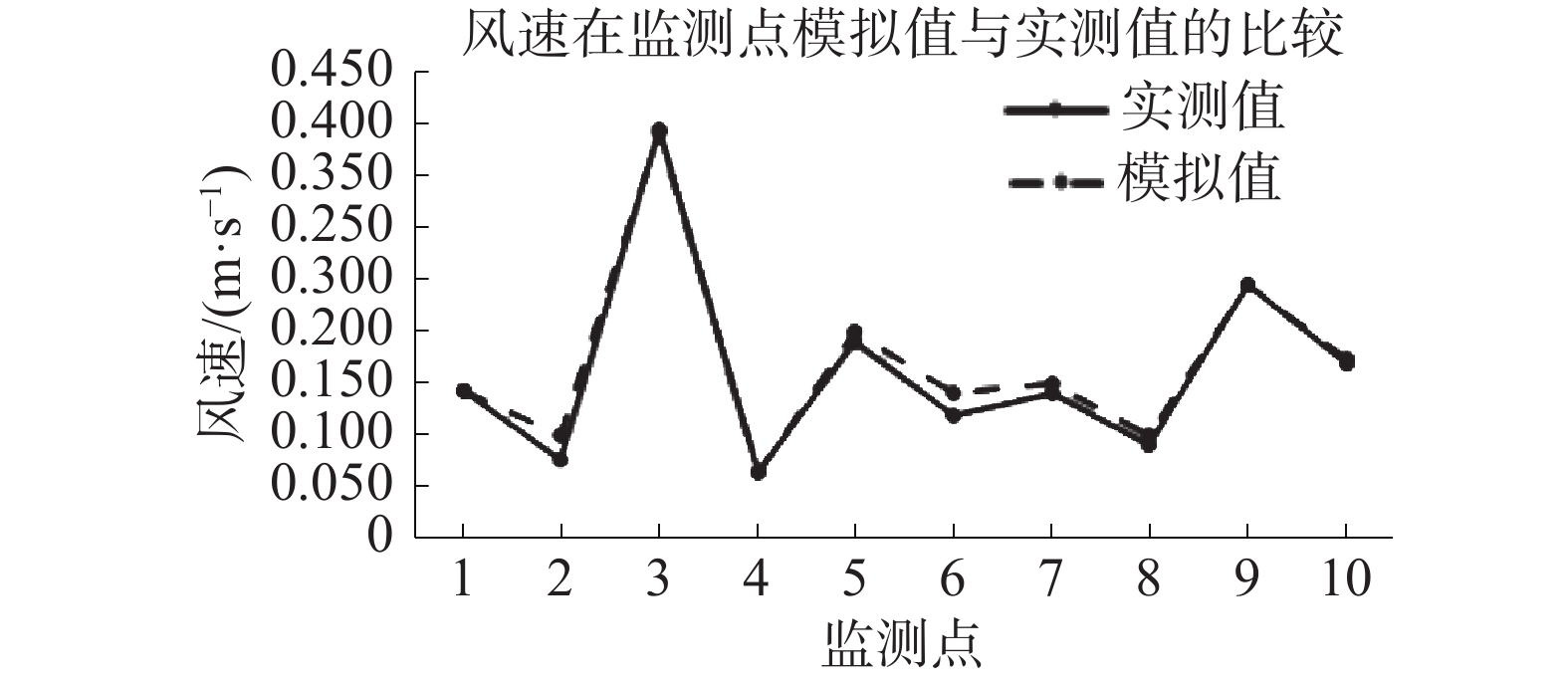
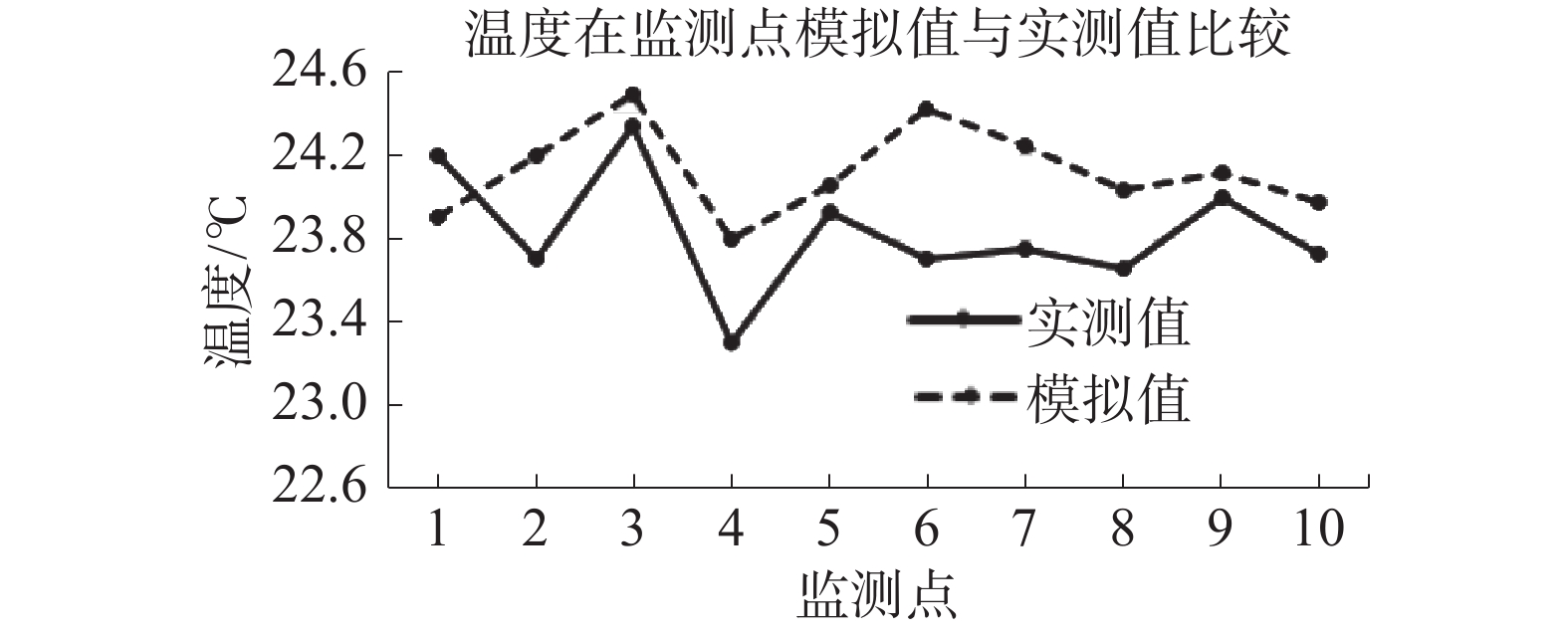
2.2 对比验证在试验期间比较10个监测点的实际测量值和使用Fluent模拟得出的计算值,其结果如图6、7所示。
|
Download:
|
| 图 6 风速在监测点模拟值与实测值的比较 | |
|
Download:
|
| 图 7 温度在监测点模拟值与实测值比较 | |
根据图6,对比不同监测点的风速,所有观测点的绝对误差的平均值为0.008 m/s,相对误差的平均值为5.54%,绝对误差和相对误差的最大值出现在监测点
根据图7,对比不同监测点的温度,10个监测点绝对误差均值为0.44 ℃,相对误差均值为4%,
温室内的速度场、温度场的均匀性受暖风扇的影响较大,因此通过在温室中改变进风口的速度和改变暖风口的位置来设计出3种改进方案,以满足植物生长的需要。方案一,升高暖风口速度,即暖风口速度从1 m/s升高到2 m/s;方案二,下移暖风口的位置,将暖风口从1.3 m处下移到1 m处,如图8所示;方案三,下移暖风口的位置至0.7 m处,如图9所示。将原温室作为方案零来进行对比,温室、植物和暖风扇的尺寸视为定量不做改变,且方案一、方案二和方案三的网格划分与方案零相同,其余边界条件的设置也相同。通过对不同方案使用Fluent进行模拟计算,比较植物冠层表面和内部的风速及温度分布情况,依此来选择拥有适宜风速温度的最适宜植物生长的方案。

|
Download:
|
| 图 8 暖风扇离地1 m时的玻璃温室模型 | |
|
Download:
|
| 图 9 暖风扇离地0.7 m时的玻璃温室模型 | |
经过改良后的方案气流分布模式基本相同:在温室上部和底部都有涡流的产生,暖风扇口附近的气流流速最大,并随着流动方向减弱,直到在东侧壁面附近开始沿温室顶部返回,温室西侧的植物表面部分和温室壁面附近风速较小,且会在植物内部的涡流处出现整个植物区域中风速的最大值。
在方案一中,从图10速度云图上看,选取的2个平面空气流速平均值为0.695 m/s,均高于方案零的0.152 m/s,且满足植物生长的最佳风速。风速在南北两侧墙处达到最大,为1.562 m/s,远高于最适宜植物生长的风速1 m/s,这样的速度容易对植物造成损伤,此时植物表面风速位于0.3~1.0 m/s的部分约占整个植物冠层的63%。在植物内部Y=0.1 m处最大风度为1.581 m/s,平均风速0.928 m/s,处在最佳气流流速范围内的区域约占27.9%,剩下的大部分区域风速均大于1 m/s,不利于植物生长,由此可知不能仅增大风速来优化温室内部的气流分布情况。
|
Download:
|
| 图 10 方案一速度场模拟 | |
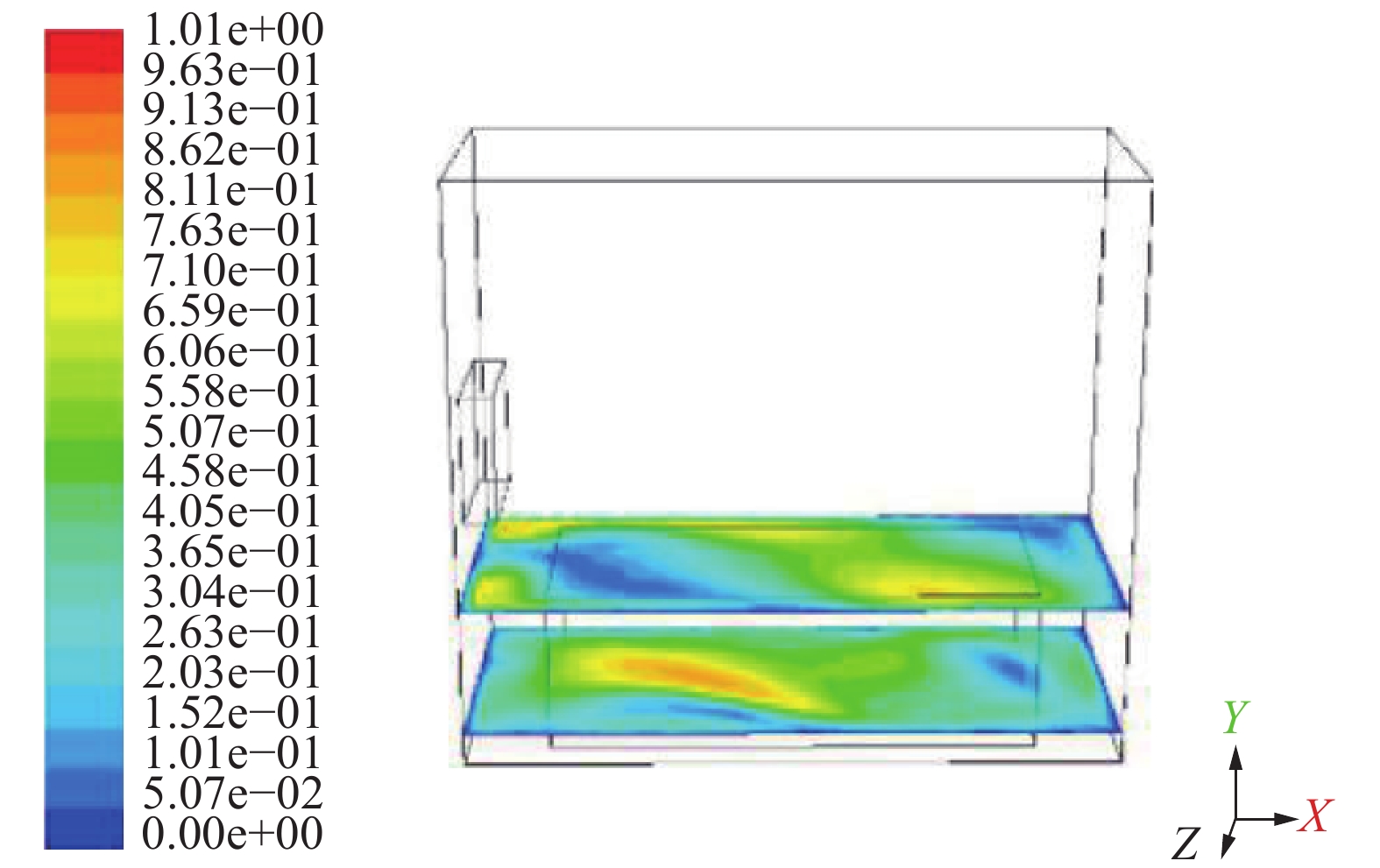
从图11方案二的云图可知,y=0.5 m处气流的流速均值为0.284 m/s,最大为0.632 m/s;y=0.1 m处平均风速为0.423 m/s,最小风速为0 m/s,最大风速为0.754 m/s,均小于方案一。处于适宜风速的占25%,虽然相对于方案零适宜风速的占比有所增加,气流的均匀性与方案一相比较好,但适宜风速的占比仍小于方案一。

|
Download:
|
| 图 11 方案二速度场模拟 | |
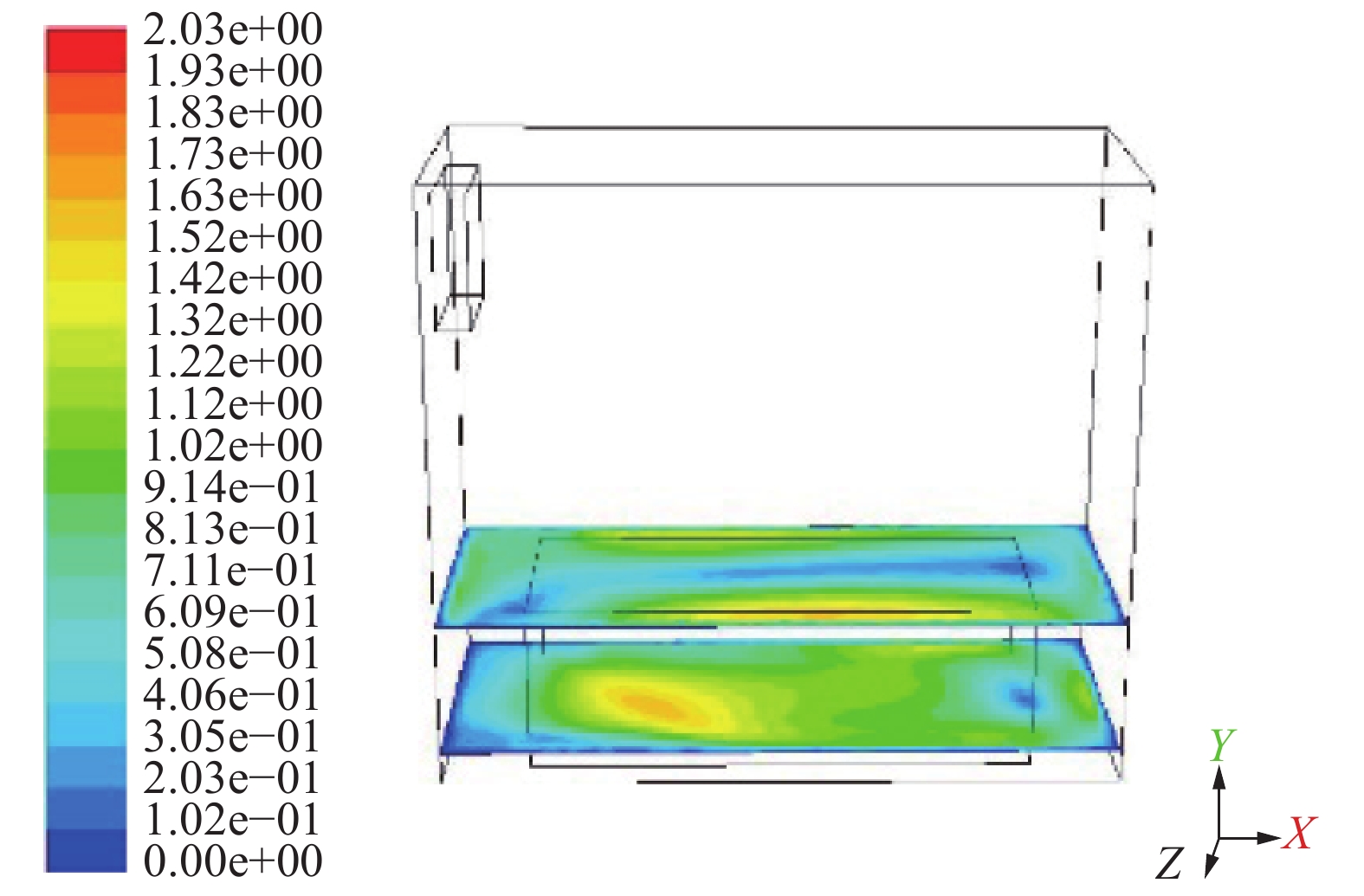
分析图12方案三的云图,选取分析的平面平均气体流速为0.383 m/s,最高流速可达0.834 m/s,均符合最佳风速。在植物部分的最低风速为0.07 m/s,大于方案零和方案二,但仍低于0.3 m/s。这时的植物冠层风速达到适宜风速的占70%,高于其他方案,且均匀性最好。
|
Download:
|
| 图 12 方案三速度场模拟 | |
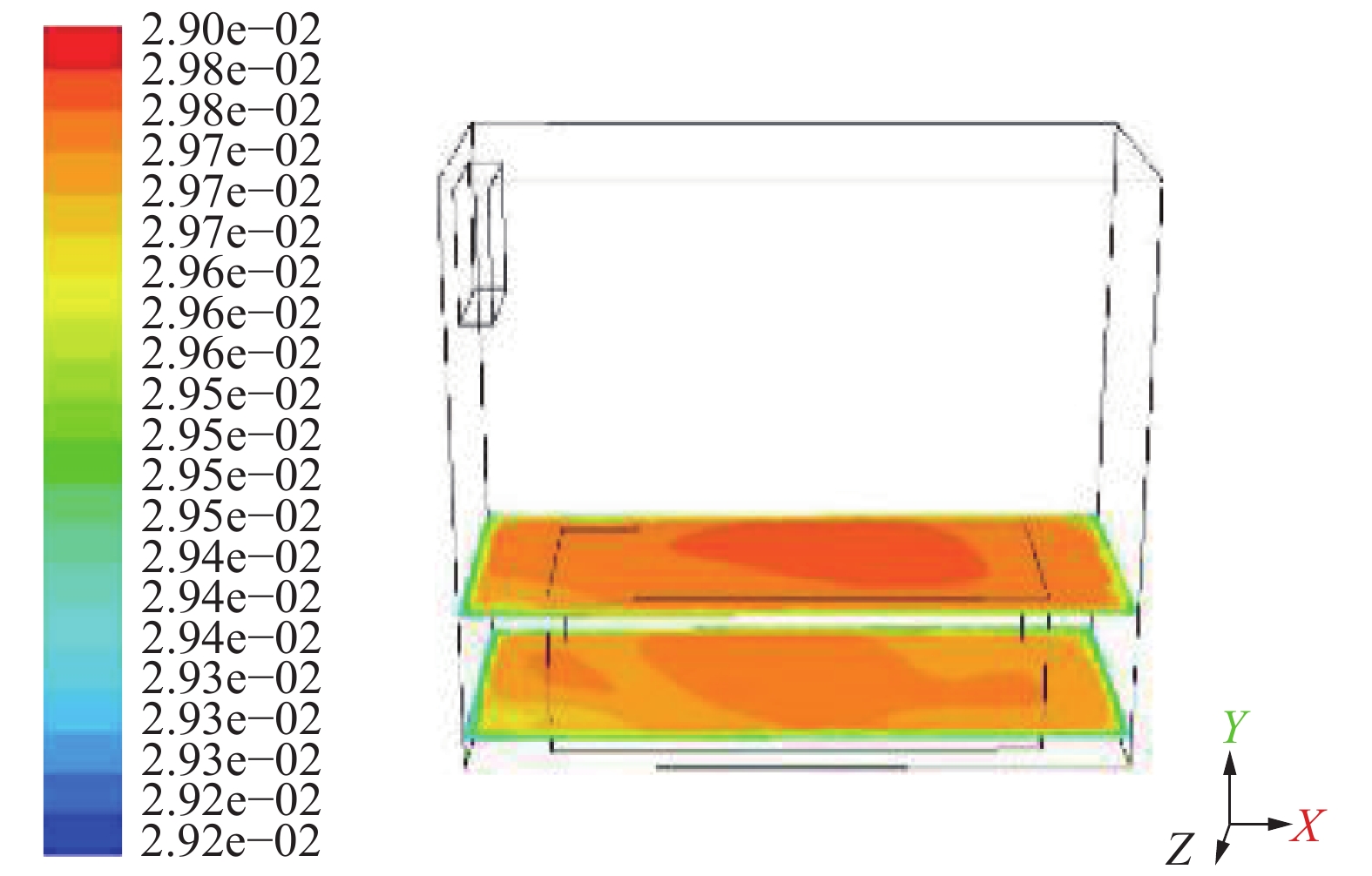
分析方案一、方案二和方案三的温度情况(图13~15),并将其与速度云图进行比对,发现气流速度较大的区域温度上升较多。
|
Download:
|
| 图 13 方案一温度场模拟 | |

|
Download:
|
| 图 14 方案二温度场模拟 | |
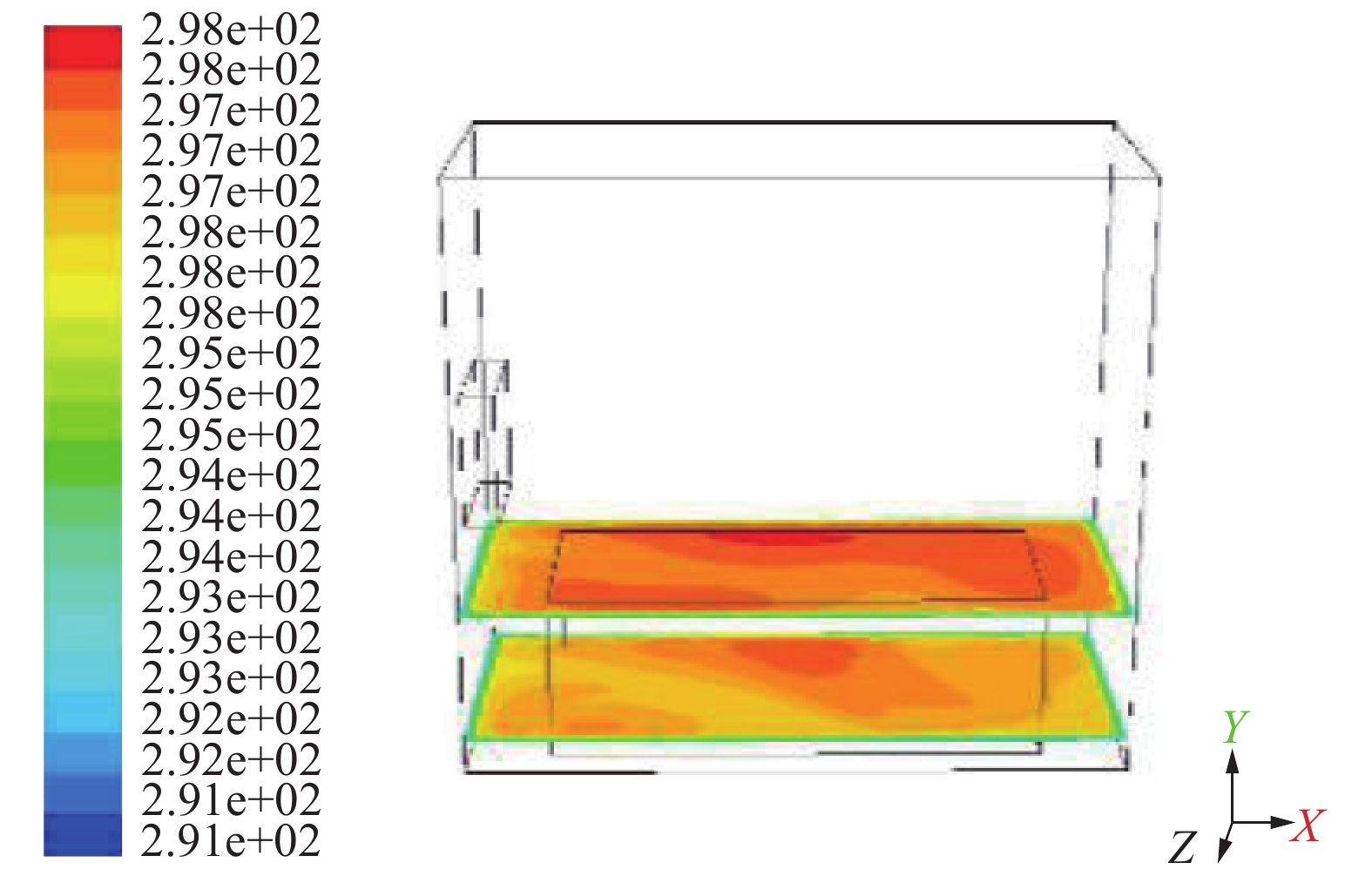
|
Download:
|
| 图 15 方案三温度场模拟 | |
3个方案的最高温度分别为24.49、24.45和24.72 ℃,平均温度为23.93、23.15和23.49 ℃,均高于方案零,且植物区域的温度分布均匀性优于方案零。就温度而言,方案一的均值和最大值都为最高,其次为方案三。
通过模拟分析实验中设计的3种温室的优化方案,可以发现:1)方案一的气流均匀性稍差,且有较多的区域风速高于最佳风速,不利于植物生长;2)方案二虽然略优于方案零,但对于气流场和温度场并不能提供有效的优化;3)方案三的气流均匀性最好,不存在流速大于1 m/s的区域,从而不会对植物的正常生长造成威胁,且风速大于方案零和方案二。总体来讲,方案三的暖风扇位置更适宜植物的生长。
4 结论1)温度数值模拟结果与实验实测结果吻合良好,表明建立的CFD模型有效,模拟玻璃温室内环境分布是可行的;
2)设计的3种结构优化方案的风速值及均匀性均优于方案零。综合考虑,方案三气流循环模式最佳,气流均匀性最好,适宜植物生长。
本文仅基于风速和暖风扇位置进行温室的优化,在之后的研究中,可考虑将添加排气扇和增加暖风扇的数量作为温室的优化方式,考虑植物在阳光下的光合作用产生的热量和外部辐射等会影响温室内部气流和温度的条件,探究温室内部气流与温度的分布情况。
| [1] |
程秀花, 毛罕平, 伍德林, 等. 栽有番茄的玻璃温室内气流场分布CFD数值模拟[J]. 江苏大学学报(自然科学版), 2010, 31(5): 510-514. DOI:10.3969/j.issn.1671-7775.2010.05.004 ( 0) 0)
|
| [2] |
汪郑邦. 现代温室供热系统的设计及运行模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2006: 79-80.
( 0) 0)
|
| [3] |
刘文合, 杨英英, 徐占洋. 基于CFD方法的温室散热系统结构优化模拟研究[J]. 灌溉排水学报, 2016, 35(4): 8-13. ( 0) 0)
|
| [4] |
周伟, 汪小旵, 李永博. 可变边界条件下的Venlo温室温度场三维非稳态模拟[J]. 农业机械学报, 2014, 45(11): 304-310. DOI:10.6041/j.issn.1000-1298.2014.11.047 ( 0) 0)
|
| [5] |
张伟建, 王新忠, 李亮亮, 等. 夏季屋顶全开型温室遮阳网降温调控的CFD分析[J]. 江苏农业科学, 2017, 45(19): 253-256. ( 0) 0)
|
| [6] |
刘焕. 基于CFD的人工光型植物工厂通风模拟与优化研究[D]. 北京: 中国农业科学院, 2018: 10-29.
( 0) 0)
|
| [7] |
段明辉. 冬季温室数值分析研究[D]. 哈尔滨: 东北农业大学, 2014: 7-9.
( 0) 0)
|
| [8] |
张艺萌. 基于CFD的寒地水稻育秧大棚环境数值模拟分析与研究[D]. 大庆: 黑龙江八一农垦大学, 2018: 28-54.
( 0) 0)
|
| [9] |
宿文, 薛晓萍, 熊宇, 等. 自然通风对日光温室气温影响的模拟分析[J]. 生态学杂志, 2016, 35(6): 1635-1642. ( 0) 0)
|
| [10] |
赵杰强, 赵云. 机械通风连栋温室的温度场CFD模拟[J]. 中国农机化学报, 2014, 35(6): 76-79. ( 0) 0)
|
| [11] |
何国敏. 现代化温室温度场数字化模拟研究[D]. 南京: 南京农业大学, 2011: 50-67.
( 0) 0)
|
| [12] |
沈敏. 食用菌工厂菇房内环境的模拟验证与优化研究[D]. 镇江: 江苏大学, 2016: 23-41.
( 0) 0)
|
| [13] |
吴飞青. 温室冬季热环境数值分析与实验研究[D]. 杭州: 浙江工业大学, 2010: 41-71.
( 0) 0)
|
| [14] |
刘焕. 基于CFD的人工光型植物工厂通风模拟与优化研究[D]. 北京: 中国农业科学院, 2018: 4.
( 0) 0)
|
| [15] |
张芳, 方慧, 杨其长, 等. 基于CFD模型的大跨度温室自然通风热环境模拟[J]. 中国农业气象, 2017, 38(4): 221-229. DOI:10.3969/j.issn.1000-6362.2017.04.003 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


