随着机械臂在工业领域内的应用越来越广泛、发展越来越迅速,机械臂轨迹跟踪的控制方法也层出不穷。机械臂轨迹跟踪的控制方法主要有PID控制、计算力矩控制、反演控制以及变结构控制等[1-4]。PID控制方法简单且易于实现,为了使机械臂的关节轨迹可以快速地跟踪上期望的关节轨迹,在使用PID控制器时通常会将控制器的P参数与D参数设置得比较大,实现快速的轨迹跟踪;计算力矩控制属于一种前馈控制方式,这种控制方式可以根据机械臂关节轨迹的变化实时调整作用给机械臂各关节的力矩;反演控制引入了微分阻尼项,可以大大提高控制系统的动态性能;变结构控制方法会给系统带来“抖振”,即当系统跟踪误差控制在零点附近时,存在很强的抖动现象,使系统不稳定[5-6]。由于机械臂自身的物理参数会受到环境及负载变化的影响,且存在非线性的关系,因此很难建立机械臂的精确数学模型,而PID控制、计算力矩控制以及反演控制均依赖于机械臂的精确数学模型,对于数学模型无法精确得到的机械臂来说,PID控制、计算力矩控制以及反演控制均存在不同程度的精度问题,难以实现机械臂的高精度轨迹跟踪控制。
对精确数学模型难以建立的系统,模糊控制的优势尤其明显,模糊控制方法不依赖被控对象的精确数学模型,但往往由于控制规则有限,存在控制精度低的问题[7]。1995年,李洪兴[8]提出了变论域模糊控制方法,所谓变论域模糊控制,就是在模糊控制的基础上,通过设计合适的伸缩因子,以论域之变应误差之变,使得实际的控制规则大幅度增加,越接近期望控制点,控制器的档级越小,因而获得比较满意的动态性能指标和稳态性能指标,控制精度与伸缩因子的设计有很大关系,设计合适的伸缩因子是变论域模糊控制器设计中的关键环节。万敏[9]教授对输入和输出论域设计了统一的指数型伸缩因子,将变论域模糊控制方法用于两关节机械臂的轨迹跟踪控制。变论域模糊控制方法在车辆工程以及机械制造等领域也获得了较多成功的应用。借助于变论域模糊控制方法,Zhao 等[10]设计了作用于输入论域的指数型伸缩因子,取得了平行二级倒立摆的控制成功。Pang等[11]用积分调节原理设计了作用于输出论域的积分型伸缩因子,实现了车辆半主动悬架控制。龙祖强[12]对输入输出论域设计了统一的指数型伸缩因子,实现了机床定位控制。
本文提出了一种新的混合型伸缩因子,设计了一种以三关节机械臂为被控对象的变论域模糊控制器,并将所设计的变论域模糊控制器应用于三关节机械臂的轨迹跟踪控制。运用MATLAB软件仿真实验验证了所设计的混合型伸缩因子在机械臂轨迹跟踪控制中的有效性,并与文献[9]提出的基于指数型伸缩因子的变论域模糊控制器在机械臂轨迹跟踪中的控制效果进行了进一步对比分析。
1 三关节机械臂动力学分析对于三关节机械臂,其动力学可以采用牛顿−欧拉方程求出,忽略摩擦力和末端负载,三关节机械臂动力学方程表示如下:
| ${{\tau }} = {{M}}({{q}}) \cdot {\ddot{ q}} + {{B}}({{q}}) \cdot [{\dot{ q}} \cdot {\dot{ q}}] + {{C}}({{q}}) \cdot [{{\dot{ q}}^2}] + {{G}}({{q}})$ |
式中:
| $[{\dot{ q}} \cdot {\dot{ q}}] = {[{\dot q_1} \cdot {\dot q_2}\;\;{\dot q_1} \cdot {\dot q_3}\;\;{\dot q_2} \cdot {\dot q_3}]^{\rm{T}}}$ |
| $[{{\dot{ q}}^2}] = {[\dot q_1^2\;\;\dot q_2^2\;\;\dot q_3^2]^{\rm{T}}}$ |
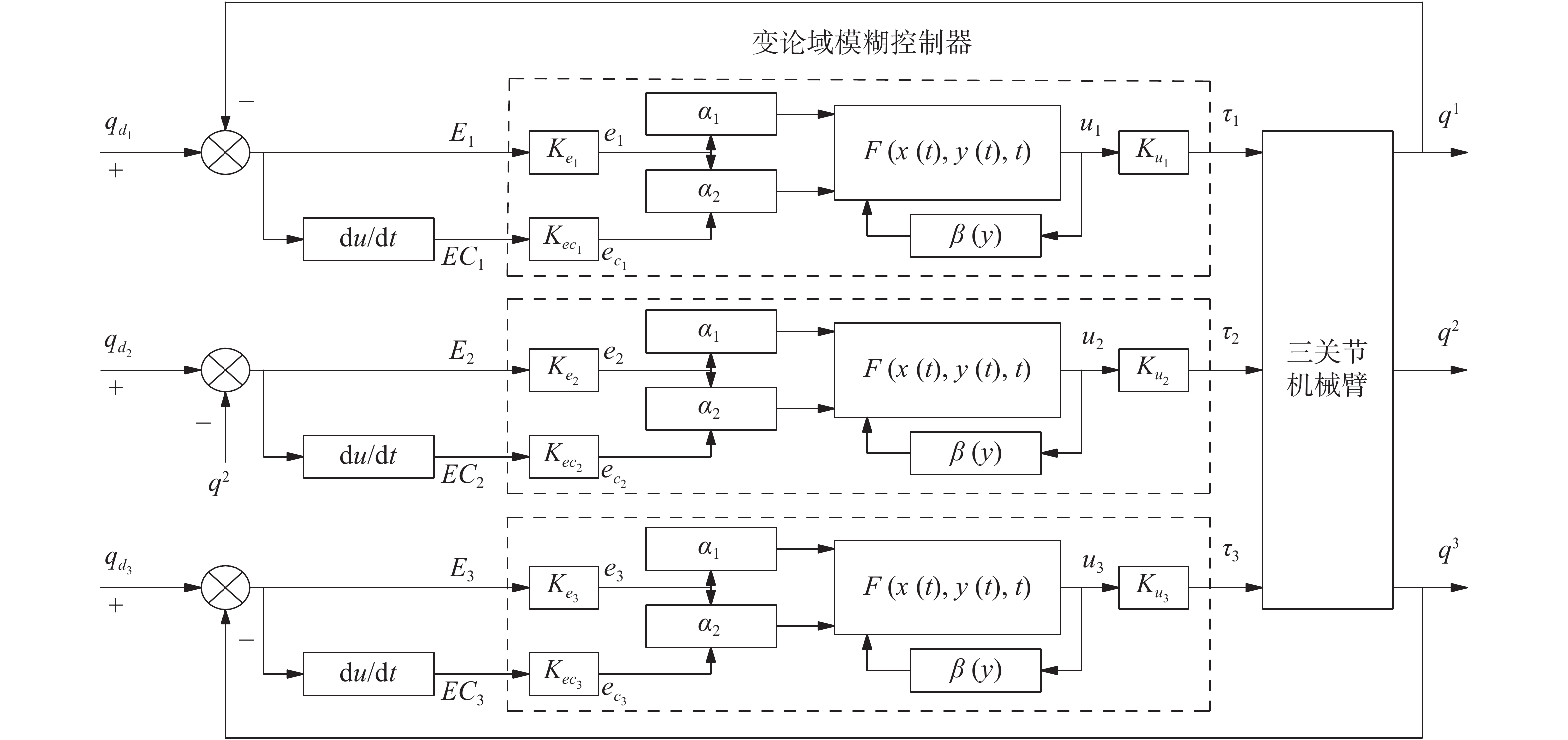
机械臂轨迹跟踪主要是通过控制器给机械臂关节施加驱动为矩,使得机械臂关节的角位移跟踪给定的期望关节角度,最终实现机械臂末端平稳地完成用户规定的作业流程。本文针对三关节机械臂的轨迹跟踪控制问题,设计了三关节机械臂轨迹跟踪的变论域模糊控制方案,其控制系统结构如图1所示。
|
Download:
|
| 图 1 三关节机械臂变论域模糊控制系统结构 | |
图1中,
2.2.1 伸缩因子的设计
变论域模糊控制器的论域随着误差的变小而收缩,随着误差的增大而膨胀。局部上看,论域收缩相当于增加规则,从插值的角度来说,规则越多,精度越高[13]。伸缩因子的选取作为变论域模糊控制器设计中的关键环节,不同类型、不同参数的伸缩因子所产生的效果大相径庭。一般地,伸缩因子满足避零性、单调性、协调性、正规性,本文提出的混合型伸缩因子满足这些特性。考虑到积分型伸缩因子会增大计算量,容易削弱实时性,同时考虑误差和误差变化率之间的相关性对精度的影响,本文将误差变化率的伸缩因子取为误差及其变化率的二元函数,动态权值
| ${{\alpha }_{1}}(x_{1}^{k})=\left\{ {\begin{array}{*{20}{l}} 1, \quad k=0 \\ {{\left| \dfrac{x_{1}^{k}}{u} \right|}^{\tau }}+\delta , \quad k=1,2,3,\cdots \\ \end{array}} \right.$ |
| ${\alpha _2}(x_1^k,x_2^k) = \left\{ {\begin{array}{*{20}{l}} 1, \quad k = 0 \\ {\left( {(1 - {w^k})\left| {\dfrac{{x_1^k}}{u}} \right| + {w^k}\left| {\dfrac{{x_2^k}}{{{u_c}}}} \right|} \right)^\tau } + \delta , \quad k = 1,2,3, \cdots \\ \end{array}} \right.$ |
| $\beta ({y^k}) = \left\{ {\begin{array}{*{20}{l}} 1, \quad k = 0 \\ {\left| {\dfrac{{{y^k}}}{V}} \right|^\tau } + \delta , \quad k = 1,2,3, \cdots \\ \end{array}} \right.$ |
式中:
2.2.2 输入输出变量的模糊化
对关节角度误差、关节角度误差变化率以及输出力矩采用区间变换的方法使其归属到无量纲的标准论域,均为
2.2.3 模糊规则的制定
根据机械臂轨迹跟踪控制的经验,当关节角度误差大或较大时,选择控制量以尽快消除误差为主;而当关节角度误差较小时,选择控制量要注意防止超调,以系统稳定性为主要出发点。可设计出如表1所示的具有25条控制规则的变论域模糊控制器规则表。
|
|
表 1 变论域模糊控制器规则表 |
2.2.4 模糊推理与逆模糊化
模糊推理与逆模糊化过程多种多样,比较典型的有重心法、中心平均法、取中位数法以及最大隶属度法等[14]。在上述多种方法中,简化计算量与保留更多有用信息是一对矛盾。本文采用将2个输入变量属于同一模糊子集的隶属度相乘之后再进行中心平均逆模糊的方法,设计出的模糊表达式如下所示:
| ${y^{k + 1}} = F({x^k},{y^k}) = \frac{{\displaystyle\sum\limits_{j = 1}^5 {\bar y_j^k\prod\limits_{i = 1}^2 {{\mu _{A_{ij}^k}}(x_i^k)} } }}{{\displaystyle\sum\limits_{j = 1}^5 {\prod\limits_{i = 1}^2 {{\mu _{A_{ij}^k}}(x_i^k)} } }}$ |
式中:
本文在MATLAB里搭建出的三关节机械臂变论域模糊控制系统仿真框图如图2所示,将3个关节的控制器封装为一个模块。控制的目标是使机械臂的各关节角度输出以尽可能高的精度快速地跟踪事先给定的参考关节角度输入。

|
Download:
|
| 图 2 三关节机械臂变论域模糊控制系统仿真框图 | |
运用上述设计的三关节机械臂变论域模糊控制系统进行轨迹跟踪控制仿真,需要先获得各关节期望角度。本文采用基于相平面的离线时间最优轨迹规划方法获得期望关节角度[15],选择如式(1)所示的笛卡尔空间轨迹,取自身弧长
| $\left\{ \begin{array}{l} {(x - 0.15)^2} + {(y + 0.15)^2}{\rm{ = }}0.36 \\ z = 0.623 \;6 \\ \end{array} \right.$ | (1) |
| $\left\{ \begin{array}{l} x = 0.6\sin (5s/3) + 0.15 \\ y = 0.6\cos (5s/3) - 0.15 \\ z = 0.623 \;6 \\ \end{array} \right.$ | (2) |
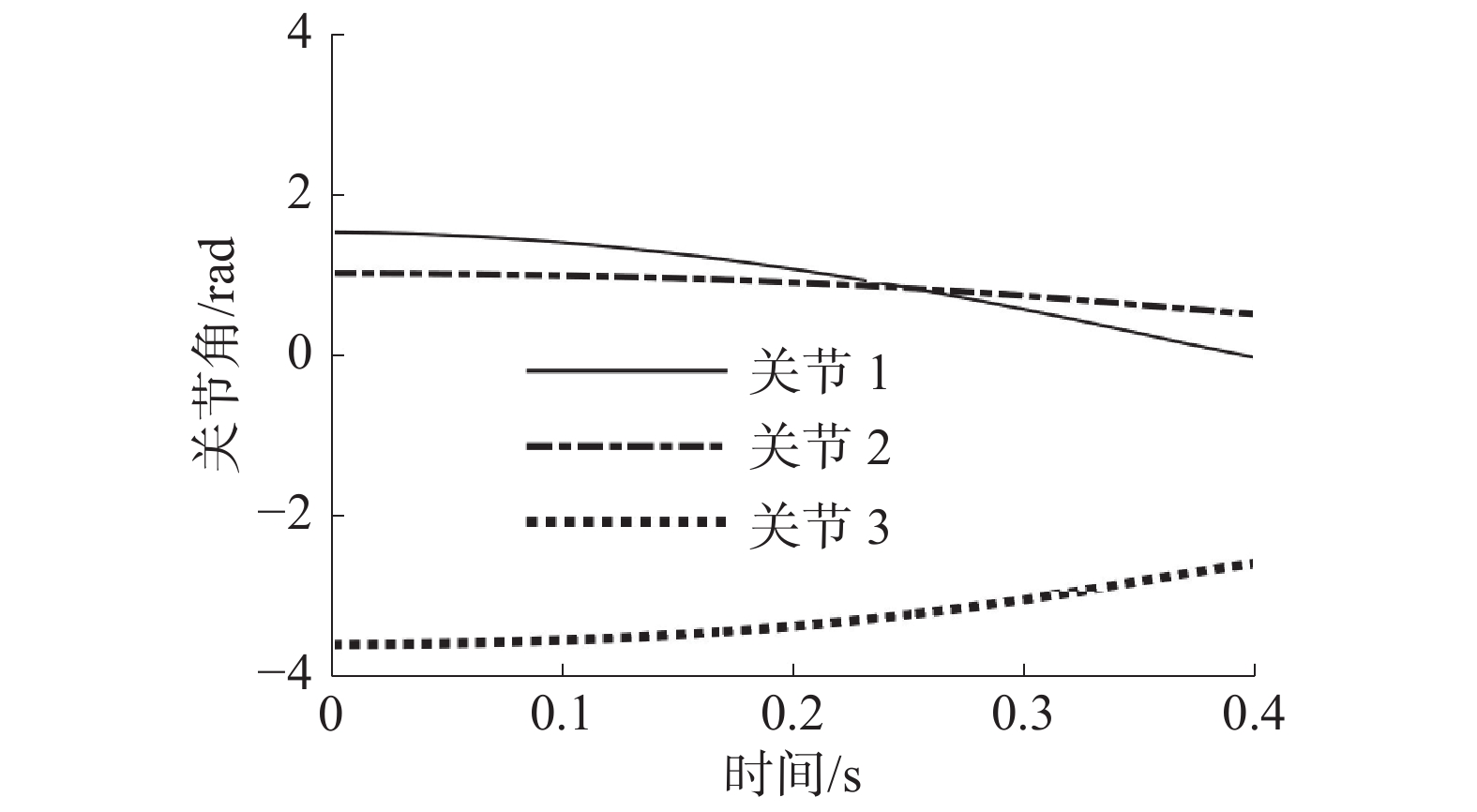
由于所获得的3个关节的轨迹均是无法显式表达的非线性函数,所以可根据得出的各个关节的轨迹获取时间−关节角度序列,选取0.02 s的时间间隔进行一次采样,则每一个采样时间对应一个关节角度值。将采样出的关节角度值作为机械臂变论域模糊控制的参考关节角度输入,即期望关节角度,如图3所示。
|
Download:
|
| 图 3 期望关节角度 | |
量化因子
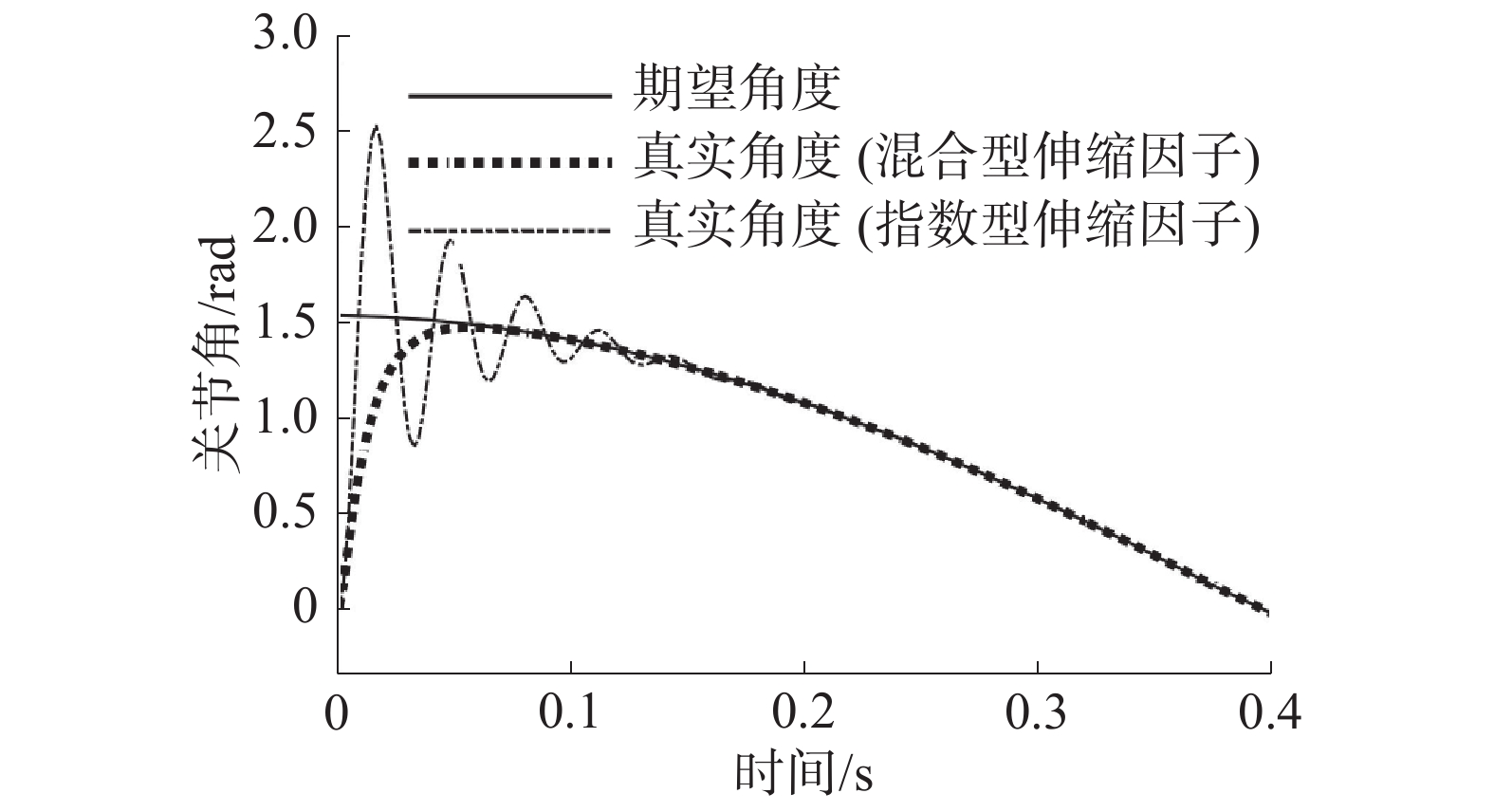
为验证提出的混合型伸缩因子的变论域模糊控制器的控制效果,本文以文献[9]中提出的指数型伸缩因子的变论域模糊控制器在三关节机械臂轨迹跟踪中的控制效果作为对比,通过Simulink中的Scope模块得到如图4~6所示的3个关节角度输出响应曲线。图4是关节1的使用指数型伸缩因子的变论域模糊控制器与本文提出的混合型伸缩因子的变论域模糊控制器分别跟踪机械臂期望关节轨迹所得出的关节角度输出对比图。
|
Download:
|
| 图 4 关节1角度输出对比响应曲线 | |
|
Download:
|
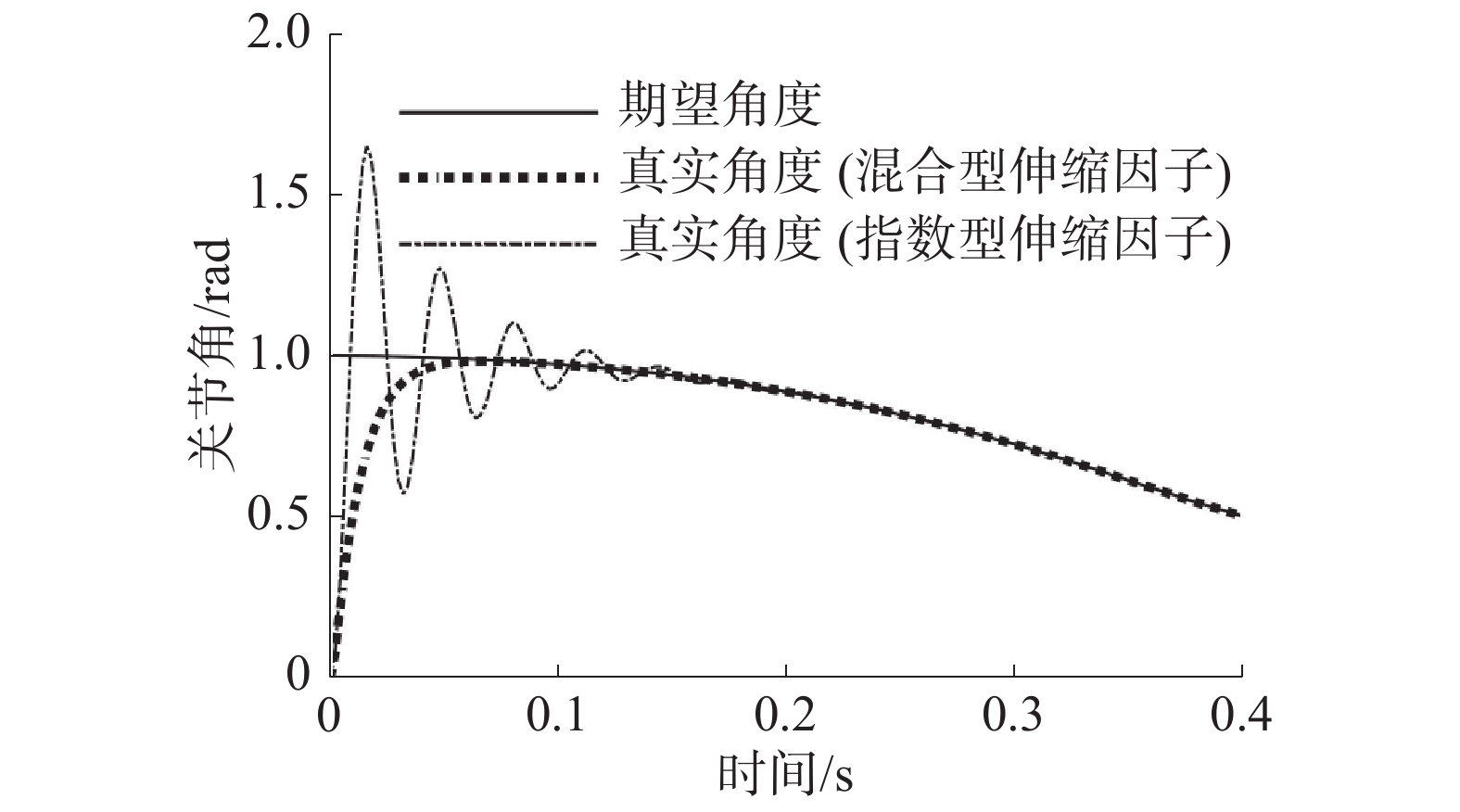
| 图 5 关节2角度输出对比响应曲线 | |

|
Download:
|
| 图 6 关节3角度输出对比响应曲线 | |
图5、6分别为关节2的关节角度输出对比图和关节3的关节角度输出对比图。表2对应图4中关节1的前10个采样点的关节角度值,表3对应图5中关节2的前10个采样点的关节角度值,表4对应图6中关节3的前10个采样点的关节角度值。
|
|
表 2 关节1角度值 |
|
|
表 3 关节2角度值 |
|
|
表 4 关节3角度值 |
由图4~6及表2~4中的数据可见,与基于指数型伸缩因子的变论域模糊控制器相比,本文设计的基于混合型伸缩因子的变论域模糊控制器能保证机械臂各关节角度输出均无超调,具有更快的响应速度。仿真结果表明本文所设计的基于混合型伸缩因子的变论域模糊控制器是行之有效的。
4 结论变论域模糊控制方法是在模糊控制的基础上,引入变论域思想,并通过对输入输出变量加入伸缩因子的方式来实现。
1)本文在MATLAB环境下,实现了一种基于混合型伸缩因子的变论域模糊控制算法,并且取得相应的仿真曲线。
2)仿真结果表明,把这种变论域模糊控制方法应用到三关节机械臂轨迹跟踪控制中,选取混合型伸缩因子,相比于指数型伸缩因子,系统的动态响应快、无超调、稳态精度高,具有较好的控制效果,显示了混合型伸缩因子在机械臂轨迹跟踪控制中的有效性和优越性,具有很强的工程实践意义和参考价值。
| [1] |
KIANG C T, SPOWAGE A, YOONG C K. Review of Control and sensor system of flexible manipulator[J]. Journal of intelligent & robotic systems, 2015, 77(1): 187-213. ( 0) 0)
|
| [2] |
汪允鹤, 李宏胜, 张伟. 柔性关节机械臂的滑模变结构控制[J]. 组合机床与自动化加工技术, 2017(10): 91-95, 100. ( 0) 0)
|
| [3] |
闫茂德, 姚盈盈, 朱旭. 分布式多电机驱动机械手系统的协调跟踪[J]. 控制工程, 2018, 25(6): 1070-1076. ( 0) 0)
|
| [4] |
夏炎. 多关节机械臂轨迹规划和轨迹跟踪控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2017: 5-6.
( 0) 0)
|
| [5] |
刘金龙. 车载液压柔性机械臂的轨迹跟踪及振动抑制方法研究[D]. 长春: 长春工业大学, 2018: 8-9.
( 0) 0)
|
| [6] |
HETEL L, FRIDMAN E, FLOQUET T. Variable structure control with generalized relays: a simple convex optimization approach[J]. IEEE transactions on automatic control, 2015, 60(2): 497-502. DOI:10.1109/TAC.2014.2331417 ( 0) 0)
|
| [7] |
PRECUP R E, HELLENDOORN H. A survey on industrial applications of fuzzy control[J]. Computers in industry, 2011, 62(3): 213-226. DOI:10.1016/j.compind.2010.10.001 ( 0) 0)
|
| [8] |
LI Hongxing. Adaptive fuzzy controllers based on variable universe[J]. Science in China series E: technological sciences, 1999, 42(1): 10-20. DOI:10.1007/BF02917053 ( 0) 0)
|
| [9] |
万敏, 安铃芝. 基于MATLAB的双关节机械手控制系统仿真研究[J]. 塑性工程学报, 2017, 24(6): 136-142. ( 0) 0)
|
| [10] |
ZHAO Guoliang, WANG Degang, SONG Zhankui. A novel tensor product model transformation-based adaptive variable universe of discourse controller[J]. Journal of the franklin institute, 2016, 353(17): 4471-4499. DOI:10.1016/j.jfranklin.2016.08.026 ( 0) 0)
|
| [11] |
PANG Hui, LIU Fan, XU Zeren. Variable universe fuzzy control for vehicle semi-active suspension system with MR damper combining fuzzy neural network and particle swarm optimization[J]. Neurocomputing, 2018, 306: 130-140. DOI:10.1016/j.neucom.2018.04.055 ( 0) 0)
|
| [12] |
龙祖强. 变论域模糊控制器的若干重要问题研究[D]. 长沙: 中南大学, 2011: 88-94.
( 0) 0)
|
| [13] |
DERELI T, BAYKASOGLU A, ALTUN K, et al. Industrial applications of type-2 fuzzy sets and systems: a concise review[J]. Computers in industry, 2011, 62(2): 125-137. DOI:10.1016/j.compind.2010.10.006 ( 0) 0)
|
| [14] |
MOHIUDDINE S A. Some new results on approximation in fuzzy 2-normed spaces[J]. Mathematical and computer modelling, 2011, 53(5/6): 574-580. ( 0) 0)
|
| [15] |
CARBONE G, GOMEZ-BRAVO F. Motion and operation planning of robotic systems[M]. Switzerland: Springer International Publishing, 2015: 45–48.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


