Joint estimation of frequency and DOA of multiple signals with spatio-temporal undersampling
随着电子战技术的日益发展,电磁环境也变得越发复杂,针对多信号的多参数估计是雷达、声呐、电子战等领域的研究热点,能够快速、准确地侦察检测多个雷达信号的频率、方向信息,对于电子对抗、雷达干扰技术而言至关重要[1−2]。在经典的空间谱估计算法MUSIC和ESPRIT的基础上提出的改进算法可以完成对多个信号的频率和DOA联合估计及配对[3−4],但是这些算法的运算量都较大,且均需要满足信号在时域和空域上的理论前提。时域方面,香农采样定理表明,奈奎斯特采样率是被采样信号的最大频率的2倍,比如为了适应电子战2~18 GHz的工作频段,需要的采样频率会很高,必须相应地增加模数转换器(analog-to-digital converter,ADC)的硬件成本和整体结构的功耗,甚至在某些特定情况下是不可实现的。同样,在空域方面若要适应电子战的工作频段,为满足相邻阵元的间距不得大于信号波长的二分之一的采样定理,需要密集的安装阵元天线,这样会带来相邻阵元间的互耦和硬件安装困难等问题,进而影响测向精度。因此,亟需寻求一种在时−空域欠采样条件下,能够对多信号多参数(频率、DOA)联合估计的新方法。
文献[5−6]提出了一种基于闭式中国余数定理(CRT)的频率、DOA联合估计方法,建立了基于闭式CRT的频率和DOA估计的模型,利用不同速率ADC采样样本(离散傅里叶变换,Discrete Fourier Transform)变换后搜索的谱峰位置构建余数完成频率估计,通过谱峰位置求得信号到达每个阵元的初相位及其相位差构建余数完成DOA估计,实现了高精度的联合估计。但该算法是针对单目标信号的参数估计,限制了其应用场合。文献[7]在闭式CRT的频率和DOA估计模型的基础上,提出了针对多目标信号的参数估计,利用信号的幅度不一致的信息,在多个信号经不同速率ADC采样样本DFT变换后得到的多个谱峰中,寻找属于同一信号的一组谱峰以构建频率余数和相位余数完成多个信号的频率和DOA联合估计,但该方法在有2个及2个以上信号的幅度一致的条件下会失效。文献[8]提出了一种能够重构多个整数的中国余数定理,并且将其应用在窄带信号的频率估计上,但其未考虑当信噪比较低时或样本数较少时谱峰位置估计不准确的问题,导致其测频精度的降低。
本文建立了一种基于重构多个整数的CRT算法和AM估计器的多信号的频率、DOA参数联合估计模型,利用多整数估计的CRT算法对稀疏线阵欠采样后的少量样本做DFT、谱峰校正,余数构建等,完成多个信号的频率估计,并根据估计完成的频率值和已经构建的余数信息在多组相位差中确定每个信号对应的一组相位差,完成频率和相位差的参数配对,进一步使用闭式CRT算法鲁棒地估计出多个信号的DOA值。本文算法只需对各个阵元接收到的多个信号做一次并行欠采样,并且谱校正后得到的谱峰信息可同时用于频率估计和DOA估计,满足目前复杂电磁环境下需要快速参数估计的需求。仿真结果证明了本文算法的高精度和低信噪比下的顽健性。
1 重构多个整数的顽健CRT算法
模数
$\left\{ {{m_1} = \varGamma {M_1},{m_2} = \varGamma {M_2}, \cdots ,{m_s} = \varGamma {M_s}} \right\}$
由
$s$
个整数构成,其中
${M_1},{M_2}, \cdots ,{M_s}$
互素。假设
$n$
个整数
${X_1},$
${X_2}, \cdots ,{X_n}$
均匀分布在
$\left( L \right.,\left. G \right]$
内,其中
$G < {\rm{lcm}}\left( {{m_1},{m_2}, \cdots ,} \right.$
$\left. {{m_s}} \right)$
,
$L \geqslant 0$
,
${\rm{lcm}}( \cdot )$
表示最小公倍数,并假设最大的整数
${m_s} > d + 2\delta $
,其中
$d = {\max _i}\{ {X_i}\} - {\min _i}\{ {X_i}\} $
,
$\delta < \dfrac{\varGamma }{4}$
;令余数
${r_{il}} = {\left\langle {{X_i}} \right\rangle _{{m_l}}}$
,
$i = 1,2, \cdots ,n$
,
$l = 1,2, \cdots ,s$
,在本文中
${\left\langle * \right\rangle _m}$
表示
$ * $
模除以
$m$
得到的余数。在实际应用中,噪声会给余数带来误差,将带有误差的余数表示为
${\tilde r_{il}} = {\left\langle {{r_{il}} + {\varDelta _{il}}} \right\rangle _{{m_l}}}$
,其中
${\varDelta _{il}}$
为余数
${r_{il}}$
的误差。
1.1 余数误差情况下的顽健重构算法
首先考虑只有一个带重构整数的情况,先前许多CRT算法[9−11]的理论前提为
$\left| {{{\tilde r}_{il}} - {r_{il}}} \right|{\rm{ = }}$
$\left| {{{\left\langle {{r_{il}} + {\varDelta _{il}}} \right\rangle }_{{m_l}}} - {r_{il}}} \right| \leqslant \delta < \dfrac{\varGamma }{4}$
,然而在实际应用中,有可能会发生
${r_{il}} + {\varDelta _{il}} > {m_l}$
或
${r_{il}} + {\varDelta _{il}} < 0$
的情况,这会导致
$\left| {{{\tilde r}_{il}}{\rm{ - }}{r_{il}}} \right|{\rm{ = }}\left| {{{\left\langle {{r_{il}} + {\varDelta _{il}}} \right\rangle }_{{m_l}}}{\rm{ - }}{r_{il}}} \right| > \delta $
,进一步使得CRT算法失效。文献[12]给出了这种问题的解决方法,其主要思想是将每个模数中的误差
${\varDelta _{il}}$
调整为一致。首先根据
${m_l} = \varGamma {M_l}$
,可以得到:
|
${\left\langle X \right\rangle _{{m_l}}} = {\left\langle X \right\rangle _{\varGamma {M_l}}} = X - \beta \varGamma {M_l}$
|
式中
$\beta $
为整数,因此
|
${\left\langle {{{\left\langle X \right\rangle }_{{m_l}}}} \right\rangle _\varGamma } = \left\langle {X - \beta \varGamma {M_l}} \right\rangle = {\left\langle X \right\rangle _\varGamma }$
|
接下来令
$Q = \left\lfloor {\dfrac{X}{\varGamma }} \right\rfloor $
,会得到
|
$\left\lfloor {\frac{{{{\left\langle X \right\rangle }_{{m_l}}}}}{\varGamma }} \right\rfloor = \frac{{{{\left\langle X \right\rangle }_{{m_l}}} - {{\left\langle X \right\rangle }_\varGamma }}}{\varGamma } = {\left\langle Q \right\rangle _{{M_l}}}$
|
可以发现,只要重构出
$Q$
就可以求得待重构的整数
$X$
。接下来将重点放在如何鲁棒、顽健地重构整数
$Q$
上。令
${r_i} = {\left\langle X \right\rangle _{{m_l}}}$
,同样地,令
${r^c} = {\left\langle X \right\rangle _\varGamma }$
、
${\tilde r_l} =$
$ {\left\langle {{r_l} + {\varDelta _l}} \right\rangle _{{m_l}}}$
、
${\tilde r^c}_l = {\left\langle {{{\tilde r}_l}} \right\rangle _\varGamma } = {\left\langle {{r^c} + {\varDelta _l}} \right\rangle _\varGamma }$
,分别用
$a$
和
$b$
表示集合
$\{ {\tilde r^c}\left| {l = 1,2, \cdots ,} \right.s\} $
中最小和最大的元素。接下来分以下几种情况进行讨论:
1)所有的
${\varDelta _l}$
均满足
$0 \leqslant {r^c} + {\varDelta _l} < \varGamma $
;
2)所有的
${\varDelta _l}$
均满足
${r^c} + {\varDelta _l} \geqslant \varGamma $
;
3)所有的
${\varDelta _l} $
均满足
${r^c} + {\varDelta _l} < 0$
;
4)一部分的
${\varDelta _l} $
满足
${r^c} + {\varDelta _l} \geqslant \varGamma $
或
${r^c} + {\varDelta _l} < 0$
。
根据上述的分析,对于情况1)来说,
${\tilde q_l} = \left\lfloor {\dfrac{{{{\tilde r}_l}}}{\varGamma }} \right\rfloor $
是
$Q$
模
${m_l}$
后得到的余数;对于情况2)、3)来说,
${\tilde q_l}$
分别是
$Q + 1$
和
$Q - 1$
模
${m_l}$
后得到的余数,可以发现在这3种情况时,
$b - a \leqslant \delta $
;而对于情况4)来说,此时
$b - a \geqslant \varGamma - 2\delta > 2\delta $
。因此当
${\tilde r_l} < 2\delta $
时令
${\tilde q_l} = \left\lfloor {\dfrac{{{{\tilde r}_l}}}{\varGamma }} \right\rfloor $
,而当
${\tilde r_l} > 2\delta $
时令
${\tilde q_l} =$
$ \left\lfloor {\dfrac{{{{\tilde r}_l}}}{\varGamma }} \right\rfloor + 1$
。综上所述,可归纳重构算法为:
1)计算余数集合
${\tilde r^c}_l = {\left\langle {{{\tilde r}_l}} \right\rangle _\varGamma }$
。
2)根据步骤1)集合中的最大值与最小值的差值,即根据
${\max _l}{\tilde r^c}_l - {\min _l}{\tilde r^c}_l = b - a$
确定
${\tilde q_l}$
和
${\tilde w_l}$
。
a)当
$b - a < 2\delta $
,令
${\tilde q_l} = \left\lfloor {\dfrac{{{{\tilde r}_l}}}{\varGamma }} \right\rfloor $
,
${\tilde w_l} = {\tilde r^c}_l$
;
b)当
$b - a \geqslant \varGamma - 2\delta $
,如果
${\tilde r^c}_l \in \left[ 0 \right.,\left. {2\delta } \right)$
,令
${\tilde q_l} = \left\lfloor {\dfrac{{{{\tilde r}_l}}}{\varGamma }} \right\rfloor $
、
${\tilde w_l} = {\tilde r^c}_l$
,若
${\tilde r^c}_l \in \left[ {\varGamma - 2\delta } \right.,\left. \varGamma \right)$
,令
${\tilde q_l} = \left\lfloor {\dfrac{{{{\tilde r}_l}}}{\varGamma }} \right\rfloor + 1$
、
${\tilde w_l} = {\tilde r^c}_l - \varGamma $
。
3)由余数
${\tilde q_l}$
通过CRT算法重构
$\tilde Q$
。
4)如果
$\tilde Q = \prod\nolimits_{l = 1}^s {{M_l} - 1} $
,且
${\tilde w_l} < 0$
,则
$\tilde X = 0$
,否则
$\tilde X = \tilde Q\varGamma + \left[ {\dfrac{{\displaystyle\sum\nolimits_{l = 1}^s {{{\tilde w}_l}} }}{s}} \right]{\text{。}}$
该算法具有顽健性,即如果余数误差小于
$\dfrac{\varGamma }{4}$
,则其重构整数的误差也小于
$\dfrac{\varGamma }{4}$
。
1.2 重构多个整数的算法
对于多个整数的情况,为了方便讨论,假设待重构整数的集合
$\{ {X_i}\} \left( {i = 1,2, \cdots ,n} \right)$
和模数的集合
$\{ {m_l}\left| {l = 1,2, \cdots ,s} \right.\} $
都是以升序排列的,会得到
$n \times s$
个余数
$\{ {r_{i,l}}\} $
,如文献[13]所提到的,2个及2个以上的整数重构的难点是整数和余之间的对应关系是未知的,即由每个模数得到的
$n$
个余数与
$n$
个整数的对应关系是未知的,所以无法使用CRT算法进行重构。
对于这种问题,首先概述主要的算法思想。由于最大的模值
${m_s} > d + 2\delta $
,所以可以在区间
$\left[ {{X_1} - \delta ,{X_n} + \delta } \right]$
找到
$X$
,并且通过余数集
${\tilde r_{is}}$
和
${\left\langle X \right\rangle _{{m_s}}}$
正确地估计
$\{ {X_i} - X\} $
的值。因此,选择估计待重构整数集的平均值
$\bar X$
,即
$\bar X = \dfrac{{\displaystyle\sum\nolimits_{i = 1}^n {{X_i}} }}{n}$
。同样地,在整数集与余数集对应关系未知的前提下,可以得到每个整数模除以同一模值的余数的和
${\tilde r_l}$
,即
${\tilde r_l} = $
$ {\left\langle {\displaystyle\sum\nolimits_{i = 1}^n {{{\tilde r}_{il}}} } \right\rangle _{{m_l}}}$
,并通过
${\tilde r_l}$
和上述的CRT算法顽健的重构整数集的和
$\displaystyle\sum\nolimits_{i = 1}^n {{X_i}} $
。为了顽健地重构
$\displaystyle\sum\nolimits_{i = 1}^n {{X_i}} $
,需要假设
$M = \varGamma \prod\nolimits_{l = 1}^s {{M_l} > nG + \varGamma + n\delta } $
,并且属于同一模值的余数误差的总和需要满足
|
$\left| {\sum\limits_{i = 1}^n {{\varDelta _{il}}} } \right| < \frac{\varGamma }{4},l \in \{ 1,2, \cdots ,s\} $
|
(1) |
为了满足式(1),可选择大于
$4n\delta $
的
$\varGamma $
,同时令
|
${\tilde r_l} = {\left\langle {\sum\limits_{i = 1}^n {{r_{il}}} + {\varDelta _{il}}} \right\rangle _{{m_l}}}$
|
对应地,
|
${\tilde r^c}_l = {\left\langle {{{\tilde r}_l}} \right\rangle _\varGamma } = {\left\langle {{{\left\langle {\sum\limits_{i = 1}^n {{r_{il}}} + {\varDelta _{il}}} \right\rangle }_{{m_l}}}} \right\rangle _\varGamma } = {\left\langle {\sum\limits_{i = 1}^n {{r_{il}}} + {\varDelta _{il}}} \right\rangle _\varGamma }$
|
根据1.1节的改进算法,仍然令
$a$
和
$b$
表示集合
${\tilde r^c}_l$
的最小值和最大值,相似地,通过
$b - a$
的值来确定
${\tilde q_l}$
和
${\tilde w_l}$
的值,因此:
|
$0 \leqslant \left| {\tilde Q - \left\lfloor {\frac{{\displaystyle\sum\limits_{i = 1}^n {{X_i}} }}{\varGamma }} \right\rfloor } \right| \leqslant 1$
|
则整数平均值
$\bar X = \left[ {\dfrac{{\displaystyle\sum\nolimits_{i = 1}^n {{X_i}} }}{n}} \right]$
可以通过式(2)求得:
|
$\tilde {\bar X} = \left[ {\frac{{\tilde Q\varGamma + \dfrac{{\displaystyle\sum\limits_{l = 1}^s {{{\tilde w}_l}} }}{s}}}{n}} \right]$
|
(2) |
接下来就是如何通过
$\tilde {\bar X}$
和
${\tilde r_{is}}$
顽健地重构各个整数
${X_i}$
。由于
$\left| {\tilde {\bar X} - {X_i}} \right| \leqslant \delta $
,可以得到
$\left| {\tilde {\bar X} - {X_i}} \right| \leqslant d + 2\delta < {m_s}$
。考虑到若有3个整数
$A$
、
$B$
和
$m$
,如果
$\left| {A - B} \right| < m$
,则
$A - B$
的值一定属于集合
$\left\{ {{{\left\langle A \right\rangle }_m} - {{\left\langle B \right\rangle }_m},{{\left\langle A \right\rangle }_m} - {{\left\langle B \right\rangle }_m} + m,} \right.$
$\left. {{{\left\langle A \right\rangle }_m} - {{\left\langle B \right\rangle }_m} - m} \right\}$
。所以为了估计
${X_i} - \tilde {\bar X}$
的值,令
$\theta $
表示
${\left\langle {\tilde {\bar X}} \right\rangle _{{m_s}}}$
,并且定义集合
|
$\varLambda = \{ \lambda _{is}^1 = {\tilde r_{is}},\lambda _{is}^2 = {\tilde r_{is}} + {m_s},\lambda _{is}^3 = {\tilde r_{is}} - {m_s}|i = 1,2, \cdots ,n\} $
|
选择其中满足条件
$\left| {\theta - \lambda _{is}^k} \right| < {m_s}$
的元素
$\lambda _{is}^k$
,
$k \in $
$\{ 1,2,3\} $
,并用其以升序构建集合
$\{ {\kappa _1},{\kappa _2}, \cdots ,{\kappa _h}\} $
。显然对于任意的
$i$
的3个元素
$\lambda _{is}^k$
,最多有2个被选择到集合
$\{ {\kappa _1},{\kappa _2}, \cdots ,{\kappa _h}\} $
,而且如果存在
$\lambda _{is}^k = \theta $
的情况,则3个元素中只有1个会被选入集合,故集合的元素个数
$h \leqslant 2n$
。接下来的工作就是基于下面的引理来确定
${X_i} - \tilde {\bar X} + {\varDelta _{is}}$
的值。
引理 对于任意的
$f \in R$
,在区间
$[f,f + {m_s})$
内至多有
$n$
个元素
${\kappa _p},{\kappa _{p + 1}}, \cdots ,{\kappa _{p + n - 1}}$
,其中
$p \in \{ 1,2, \cdots ,h - $
$n + 1\} $
。
关于引理的证明见文献[8]。
因此,
$\{ \tilde {\bar X} - \theta + {\kappa _p},\tilde {\bar X} - \theta + {\kappa _{p + 1}}, \cdots ,\tilde {\bar X} - \theta + {\kappa _{p + n - 1}}\} $
包含了所有
$\{ {X_i} + {\varDelta _{is}}\} $
可能的取值。令
${\varPhi _p} =\displaystyle \sum\nolimits_{l = p}^{n + p - 1} {{\kappa _l}} $
,其中
$p = 1,2, \cdots ,h - n + 1$
,同样使其按升序排列,一定会有连续的
$n$
个值的和等于整数的和,即一定会有
${\varPhi _\gamma }$
,满足
${\varPhi _\gamma } = \tilde Q\varGamma + {\tilde w_s} - n\tilde {\bar X} + n\theta = n\theta $
,并且由于
${\varPhi _p}$
的单调性,
$\gamma $
是唯一的,故由于
$\left| {{X_i} - \tilde {\bar X}} \right| + \delta < {m_s}$
,待重构的
$n$
个整数为
|
${\tilde X_i} = \bar X - \theta + {\kappa _{\gamma + i - 1}},i = 1,2, \cdots n$
|
2 欠采样的频率估计方法
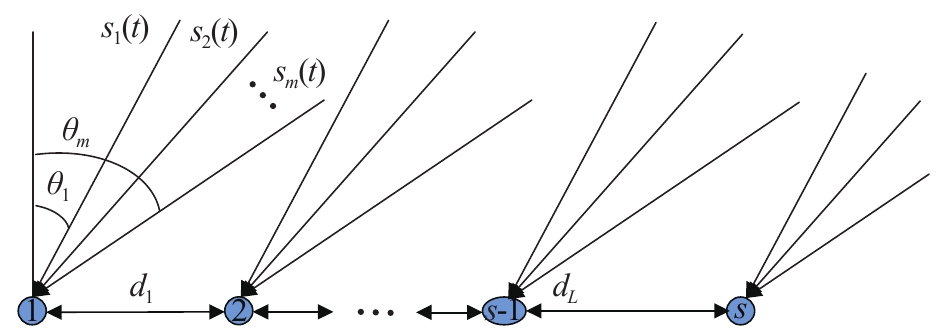
首先给出系统模型,如图1所示,由
$s(s > 2)$
个阵元天线组成非均匀线阵,假设有
$m$
个同时到达的远场信号,不失一般性,将其表示为单频复指数形式:
|
${S_i} = {A_i}\exp ({\rm{j}}2{\rm{\pi }}{f_i}t + {\rm{j}}{\varphi _i})$
|
式中:
${A_i}$
和
${f_i}$
分别为各个信号的幅度和频率;
${\varphi _i}$
为信号的初相位;
$i = 1,2, \cdots ,m$
。假设各个信号的频率
${f_i}$
都不相同,由于噪声和阵列阵元的间距,第
$l$
个阵元接收到的信号为:
|
${S_l} = \sum\limits_{i = 1}^m {{A_i}\exp ({\rm{j}}2{\rm{\text π}}{f_i}t + {\rm{j}}{\varphi _{il}}) + {\zeta _l}} (t)$
|
式中:
${\varphi _{il}}$
为第
$i$
个信号到达第
$l$
个阵元的初相位;
${\zeta _l}(t)$
为高斯白噪声;
$l = 1,2, \cdots ,s$
。从任一时刻开始,
$s$
个阵元分别以
${f_{s1}}\sim{f_{ss}}$
的采样速率对同时到达的
$m$
个信号进行欠采样,并且得到了
$s$
路样本,假设每路的样本数为
$N$
,则第
$l$
个阵元得到的样本序列为:
|
${s_l}(n) = \sum\limits_{i = 1}^m {{A_i}\exp \left( {{\rm{j}}2{\rm{\text π}}{f_i}\frac{n}{{{f_{sl}}}} + {\rm{j}}{\varphi _{il}}} \right) + } {\zeta _l}\left( {\frac{n}{{{f_{sl}}}}} \right)$
|
式中:
${f_{s1}}\sim{f_{ss}}$
为时域欠采样采样速率,均远小于信号频率;
$l = 1,2, \cdots ,s$
;
$n = 0,1, \cdots ,N - 1$
。接下来用之前介绍的CRT重构算法解决时域欠采样带来的频谱模糊问题,并完成准确的测频。
对
$s$
路欠采样样本序列做DFT,并进行谱峰搜索,得到谱峰位置
${k_{il}}$
,则各个信号的频率
${f_i}$
可表示为:
|
${f_i} = {n_{il}}{f_{sl}} + ({k_{il}} + {\delta _{il}})\frac{{{f_{sl}}}}{N}$
|
(2) |
式中:
${n_{il}}$
为模糊倍数;
${\delta _{il}}$
为频偏小数,且
$\left| {{\delta _{il}}} \right| \leqslant 0.5$
,也是影响测频精度的重要因素,
${\delta _{il}}$
可由AM估计器进行校正,进而得到更精确的余数;
$i = 1,2, \cdots ,$
$M;\;\;l = 1,2, \cdots ,s$
。可将式(3)转变为中国余数定理模型
|
${X_i} = {n_{il}}{m_l} + {r_{il}}$
|
式中:待测的信号频率
${f_i}$
对应CRT中的被除数
${X_i}$
;采样频率
${f_{sl}}$
对应CRT中的模数
${m_l} = \varGamma {M_l}$
,
$\varGamma $
为最大公约数,
${M_l}$
为互素的整数;
$i = 1,2, \cdots ,M$
;
$l = 1,2, \cdots ,s$
。而重构所需的余数为
|
${r_{il}} = {\left\langle {{X_i}} \right\rangle _{{m_l}}} = ({k_{il}} + {\delta _{il}})\frac{{{f_{sl}}}}{N}$
|
(3) |
对于
$m$
个信号的情况,在
$s$
路样本序列DFT变换后,都会搜索得到
$m$
个谱峰,而在
$m$
个信号的幅度有2个及2个以上是相同的情况下,不能在每路
$m$
个谱峰中寻找对应同一信号的
$s$
个谱峰,即不能构造出
$m$
组余数
$\{ {r_{i1}},{r_{i2}}, \cdots {r_{is}}\} $
,进而分别进行
$m$
次闭式CRT算法重构出
$m$
个信号的频率。
考虑到第1章提出的重构多个整数的CRT算法,其前提条件为
${m_s} > d + 2\delta $
,即模数组中的最大模值需要大于多个整数中最大值与最小值的差值,结合本节的频率估计模型,即最大的欠采样速率
${f_{ss}}$
需要大于信号带宽(
${f_m} - {f_1}$
),所以该CRT算法适用于窄带信号中的多个频率估计,算法流程如下:
1)对
$s$
路欠采样样本做
$N$
点的DFT变换,谱峰搜索后得到谱峰位置
${k_{il}}$
,
$i = 1,2, \cdots ,m$
,
$l = 1,2, \cdots ,s$
,即每路样本得到
$m$
个谱峰位置。
2)校正每路样本的谱峰位置对应的频偏小数,对于第
$l$
路欠采样样本,将
$m$
频偏小数的值进行初始化
$\delta _{il}^{(0)} = 0$
,
$i = 1,2, \cdots ,m$
,按式(5)进行计算得到迭代值
$\delta _{il}^l$
。
|
$\left\{ \begin{aligned} {C_{l,q}} = & \sum\nolimits_{k = 0}^{N - 1} {{s_l}(n)\exp \left( { - {\rm{j}}2{\rm{\text π}}\frac{{\left( {{k_{il}} + \delta _{il}^{l - 1} + q} \right)}}{N}} \right)} \\ \delta _{il}^l = & \delta _{il}^{l - 1} + 0.5{\rm{Re}} \left( {\frac{{{C_{l,0.5}} + {C_{l, - 0.5}}}}{{{C_{l,0.5}} - {C_{l, - 0.5}}}}} \right) \\ \end{aligned} \right.$
|
(4) |
式中:
$q = \pm 0.5$
;
${\rm{Re}} \left( \cdot \right)$
表示取其实部。将其迭代2次以上的收敛值做为频偏小数的估计值
$\delta _{il}^l$
,
$i = 1,$
$2, \cdots ,m$
,
$l = 1,2, \cdots ,s$
。
3)将谱峰位置
${k_{il}}$
、频偏小数
$\delta _{il}^l$
代入式(4)得到校正后带有误差频率余数估计值
${\tilde r_{il}}$
,
$i = 1,2, \cdots ,m$
,
$l = 1,2, \cdots ,s$
。
4)计算对应同一模数
${m_l}$
的余数估计值的和
${\tilde r_l} = {\left\langle {\displaystyle\sum\limits_{i = 1}^m {{{\tilde r}_{il}}} } \right\rangle _{{m_l}}}$
,
$l = 1,2, \cdots ,s$
。
5)将参数
${\tilde r_l}$
、
${m_l}\left( {{f_{sl}}} \right)$
,
$l = 1,2, \cdots ,s$
代入到重构多个整数的CRT算法中,得到
$m$
个信号频率的平均值,进一步得到
$m$
个信号的频率估计值
${\tilde f_i}$
。
3 欠采样的DOA估计方法
3.1 基于CRT算法的DOA估计模型
阵列结构如图1所示,由相位干涉仪原理可知,由信号到达阵元的波程差会产生相位差,在任一时刻,阵元
$j$
和阵元
$j + 1$
的接收到的信号
${S_i}$
的相位差为:
|
$\varDelta {\bar \varphi _{ij}} = 2{\text{π}} {d_j}\frac{{\sin\; {\theta _i}}}{{{\lambda _i}}}$
|
(6) |
式中:
$i = 1,2, \cdots ,m$
;
$j = 1,2, \cdots ,s - 1$
;
${\lambda _i}$
为信号
${S_i}$
的波长;
${\theta _i}$
为信号
${S_i}$
的入射角度;
${d_j}$
为阵元间距,当
${d_j} > \dfrac{{{\lambda _i}}}{2}$
,则会产生相位模糊问题,即:
|
$\Delta {\bar \varphi _{ij}} = 2{\rm{\pi }}{n_{ij}} + \Delta {\varphi _{ij}},\Delta {\varphi _{ij}} \in \left[ {0,2{\rm{\text π}}} \right)$
|
(6) |
式中:
${n_{ij}}$
为模糊倍数;
$\Delta {\varphi _{ij}}$
为真实情况下测得的相位差。由式(6)、(7)可得:
|
$2{\rm{{\text π}}}{d_j}\frac{{\sin {\theta _i}}}{{{\lambda _i}}} = 2{\rm{{\text π}}}{n_{ij}} + \Delta {\varphi _{ij}}$
|
(7) |
将式(8)的两边同时乘相同的参数
$\dfrac{{{d_0}}}{{2{\rm{\text π}}{d_j}}}$
得:
|
${d_0}\frac{{\sin {\theta _i}}}{{{\lambda _i}}} = {n_{ij}}\left( {\frac{{{d_0}}}{{{d_j}}}} \right) + \frac{{\Delta {\varphi _{ij}}{d_0}}}{{2{\rm{\text π}}{d_j}}}$
|
式中
${d_0}$
和
${d_j}$
定义为:
|
$\left\{\!\! \begin{array}{l} {d_0} = C{M_\theta }\prod\nolimits_{k = 1}^{s - 1} {{\varGamma _{{\theta _k}}}} \\ {d_j} = C\prod\nolimits_{k = 1}^{s - 1} {\frac{{{\varGamma _{{\theta _k}}}}}{{{\varGamma _{{\theta _j}}}}}} \\ \end{array} \right.$
|
式中:
$C$
为非负常数;
${M_\theta }$
为任意正整数;
${\varGamma _{{\theta _1}}}\sim{\varGamma _{{\theta _{(s - 1)}}}}$
为互素的整数。令待重构的整数
${Q_{{\theta _i}}} = {d_0}\dfrac{{\sin {\theta _i}}}{{{\lambda _i}}}$
分别定义模为
${m_l} = \dfrac{{{d_0}}}{{{d_j}}} = {M_\theta }{\varGamma _{{\theta _j}}}$
,相位差构造的对应CRT中的余数为
${r_{{\theta _{ij}}}} = \dfrac{{\Delta {\varphi _{ij}}{d_0}}}{{2{\rm{\text π}}{d_j}}} = \Delta {\varphi _{ij}}\dfrac{{{M_\theta }{\varGamma _{{\theta _j}}}}}{{2{\rm{\text π}}}}$
,即
|
${r_{{\theta _j}}} = {\left\langle {{Q_{{\theta _i}}}} \right\rangle _{{m_l}}}$
|
所以,只要我们得到每个信号在阵元间的相位差,就可以通过CRT算法重构出
${Q_{{\theta _i}}}$
,在频率值和相位差余数配对后,通过式(9)求得DOA的估计值,其中
${\lambda _0}$
的值可由第2章中测得频率结果得到。
|
${\theta _i} = \arcsin \frac{{{Q_{{\theta _i}}}{\lambda _0}}}{{{d_0}}}$
|
(8) |
3.2 相位差余数与信号频率的配对
考虑到DFT变换后谱峰位置对应的相位为信号
${S_i}$
到达阵元
$l$
的初相位,记为
${\varphi _{pil}}$
。由第2章分析可知,对于
$m$
个信号同时到达
$s$
个阵元的情况,可以通过
$s$
路样本序列得到
$m \times s$
个谱峰位置。同样我们可以得到
$m \times s$
个初相位,即每个阵元可以得到
$m$
个初相位。只有在相邻阵元的初相位中,选择属于同一信号频率的2个初相位,才能得到正确的相位差,进而得到正确的DOA估计值。
不同整数
${X_i}$
模除同一模值
$m$
得到的余数为
${r_i}$
,定义
${P_0}$
为余数
${r_a}$
和
${r_b}$
不相等的概率,其中
$i = 1,$
$2, \cdots n$
,
$a \ne b$
。其值为:
|
${P_0} > \prod\nolimits_{i = 1}^n {(1 - \frac{{(i - 1)s}}{m})} $
|
(9) |
表1中
$s$
为模值的个数。由式(10)可知,当模值
$m$
相对较大时,余数
${r_a}$
和
${r_b}$
不相等的概率极大,特别是对应第2章中的欠采样采样频率,一般都在100 MHz以上,此时
${P_0}$
几乎为1。所以,可以认为,对于任一阵元的样本序列
${s_l}(n)$
,通过DFT变换后的谱峰位置得到的频率余数值
表 1(Tab. 1
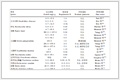
表 1 s个阵元采集m个信号得到的余数及对应初相位
| 阵元1 |
阵元2 |
$ \cdots $
|
阵元s
|
|
${\tilde r_{11}},{\varphi _{p11}}$
|
${\tilde r_{12}},{\varphi _{p12}}$
|
$ \cdots $
|
${\tilde r_{1s}},{\varphi _{p1s}}$
|
|
${\tilde r_{21}},{\varphi _{p21}}$
|
${\tilde r_{22}},{\varphi _{p22}}$
|
$ \cdots $
|
${\tilde r_{2s}},{\varphi _{p2s}}$
|
|
$ \vdots $
|
$ \vdots $
|
$ \cdots $
|
$ \vdots $
|
|
${\tilde r_{m1}},{\varphi _{pm1}}$
|
${\tilde r_{m2}},{\varphi _{pm2}}$
|
$ \cdots $
|
${\tilde r_{ms}},{\varphi _{pms}}$
|
|
表 1 s个阵元采集m个信号得到的余数及对应初相位
|
|
${\tilde r_{il}} = ({k_{il}} + {\delta _{il}})\frac{{{f_{sl}}}}{N}$
|
式中
$i = 1,2, \cdots ,m$
。
如表1所示,每列的余数都是不相同的,同时,我们由谱峰位置得也可以到对应的初相位
${\varphi _{pil}}$
。
在频率估计后,
$m$
个信号的频率估计值
${\tilde f_i}$
和
$s$
个阵元的采样频率
${f_{sl}}$
均为已知的,故可以通过
${\tilde f_i}od {f_{sl}}$
,
$l = 1,2, \cdots ,s$
,得到信号
${S_i}$
的
$s$
个余数
${r_{il}}$
,并依次用余数
${r_{i1}}\sim{r_{is}}$
,在表中每列找到
${\tilde r_{i1}}\sim{\tilde r_{is}}$
对应的的位置,进而得到信号
${S_i}$
到达
$s$
个阵元的
$s$
个初相位
${\varphi _{pi1}}\sim{\varphi _{pis}}$
,并求得信号
${S_i}$
的
$s - 1$
个相位差
$\varDelta {\varphi _{ij}}$
,
$ j = 1,2, \cdots s - 1$
。同理,依次可以得到
$m$
个信号的
$m \times (s - 1)$
个相位差。所以此时第1章的重构多个整数的CRT算法适用,而考虑到该算法的理论前提
$\left| {\displaystyle\sum\limits_{i = 1}^n {{{\mathit{\Delta}}_{il}}} } \right| < \dfrac{\varGamma }{4},l \in \{ 1,2, \cdots s\} $
,即要求通过谱峰位置得到所有信号到达同一阵元的初相位的误差的和小于DOA估计模型中的
${M_\theta }$
的
$\dfrac{1}{4}$
,这个条件对于相位测量是比较苛刻的。但与频率估计模型不同的一点是,对于DOA估计来说,经过上述方法的参数配对,属于同一信号带有DOA信息的待重构整数
${Q_{{\theta _i}}}$
的
$s$
个相位差余数
${\tilde r_{{\theta _j}}} = \dfrac{{\Delta {\varphi _{ij}}{d_0}}}{{2{\rm{\text π}}{d_j}}}$
是已知的,也就是每个待重构整数与余数集的对应关系是已知的。所以我们可以分别使用
$m$
次传统的闭式CRT算法求得
$m$
个整数
${Q_{{\theta _i}}}$
的值,这样相较于直接重构多个整数的算法,我们就把相位测量误差的限度降低了
$m$
倍。故DOA估计算法流程如下:
1)对于第
$l$
路样本,根据谱峰位置对应的幅值求得个信号到达阵元
$l$
的初相位
${\varphi _{pil}},i = 1,2, \cdots ,m$
,并由频率估计过程中得到的频偏小数
$\delta _{il}^l$
,通过式(11)对信号初相位进行校正:
|
${\varphi _{il}} = {\varphi _{pil}} - \frac{{N - 1}}{N}\delta _{il}^l{\rm{\text π}}$
|
(10) |
式中
$i = 1,{\rm{2}}, \cdots ,m$
。
2)通过测得的
$m$
个频率值
${\tilde f_i}$
模除采样频率
${f_{sl}}$
的余数值选择同一信号在频率估计过程中对应的
$s$
个余数的位置,在该位置得到同一信号到达每个阵元校正后的初相位值
${\varphi _{il}}$
,并根据式(12)求得相位差。
|
$\Delta {\varphi _{ij}} = {\varphi _{il}} - {\varphi _{il - 1}}$
|
(11) |
式中
$j = 1,2, \cdots ,l - 1$
。
3)通过相位差
$\{ \Delta {\varphi _{ij}},j = 1,2, \cdots ,l - 1\} $
构成的相位差余数
$\{ {r_{{\theta _{ij}}}},j = 1,2, \cdots ,l - 1\} $
和闭式CRT算法求得信号
${S_i}$
的DOA估计值
${\tilde \theta _i}$
,分别对
$m$
组相位差余数使用CRT算法即可求得
$m$
个信号的DOA估计值。
4 仿真实验
设有3个远场信号同时到达阵列,阵列由4个阵元组成,假设信号的频率在
$1 \;500\sim 2 \;150 \;{\rm{MHz}}$
,根据本文提出的欠采样下的频率和DOA联合估计方法,最大模值需大于多个整数中最大值与最小值的差的条件。阵元中最大的采样频率
${f_{s4}}$
应设置为
${\rm{650}} \;{\rm{MHz}}$
,选取对应CRT算法参数中的最大公约数
$\varGamma = 50 \times {10^6}$
,则一组互素模数中最大模数
${M_4}{\rm{ = 13}}$
。为满足时域欠采样的条件,选取3个小于
${M_4}$
的模数构成互素的模数组
$[{M_1},{M_2},{M_3},{M_4}] = [3,5,$
$11,13]$
,所以对应的4个阵元ADC的采样频率分别为
${f_{s1}} = {\rm{150}} \;{\rm{MHz}}$
、
${f_{s2}} = {\rm{250}} \;{\rm{MHz}}$
、
${f_{s3}} = {\rm{550}} \;{\rm{MHz}}$
、
${f_{s4}} = $
${\rm{650}} \;{\rm{MHz}}$
。显然阵元ADC的采样速率远小于信号的频率,属于时域欠采样。非负常数
$C$
取为0.1,互质参数
$\left[ {{\varGamma _{{\theta _1}}},{\varGamma _{{\theta _2}}},{\varGamma _{{\theta _3}}}} \right] = \left[ {3,5,7} \right]$
,即阵元间距为
$\left[ {{d_1},{d_2},} \right.$
$\left. {{d_3}} \right] = \left[ {{\rm{0}}{\rm{.35}}\; {\rm{m,0,21}}\; {\rm{m,0}}{\rm{.15}} \;{\rm{m}}} \right]$
,小于入射信号的半波长,属于空域欠采样。
本节实验采用检测概率
${p_d}$
和均方根误差(root mean square error, RMSE)对算法的顽健性、抗噪性以及参数测量精度进行考量。假设每个阵列的接收特性相同并且是相互独立的,欠采样样本序列的长度
$N = 2\;000$
,噪声是均值为零的高斯白噪声,在每个信噪比(SNR)条件下进行1 000次Monte Carlo实验。
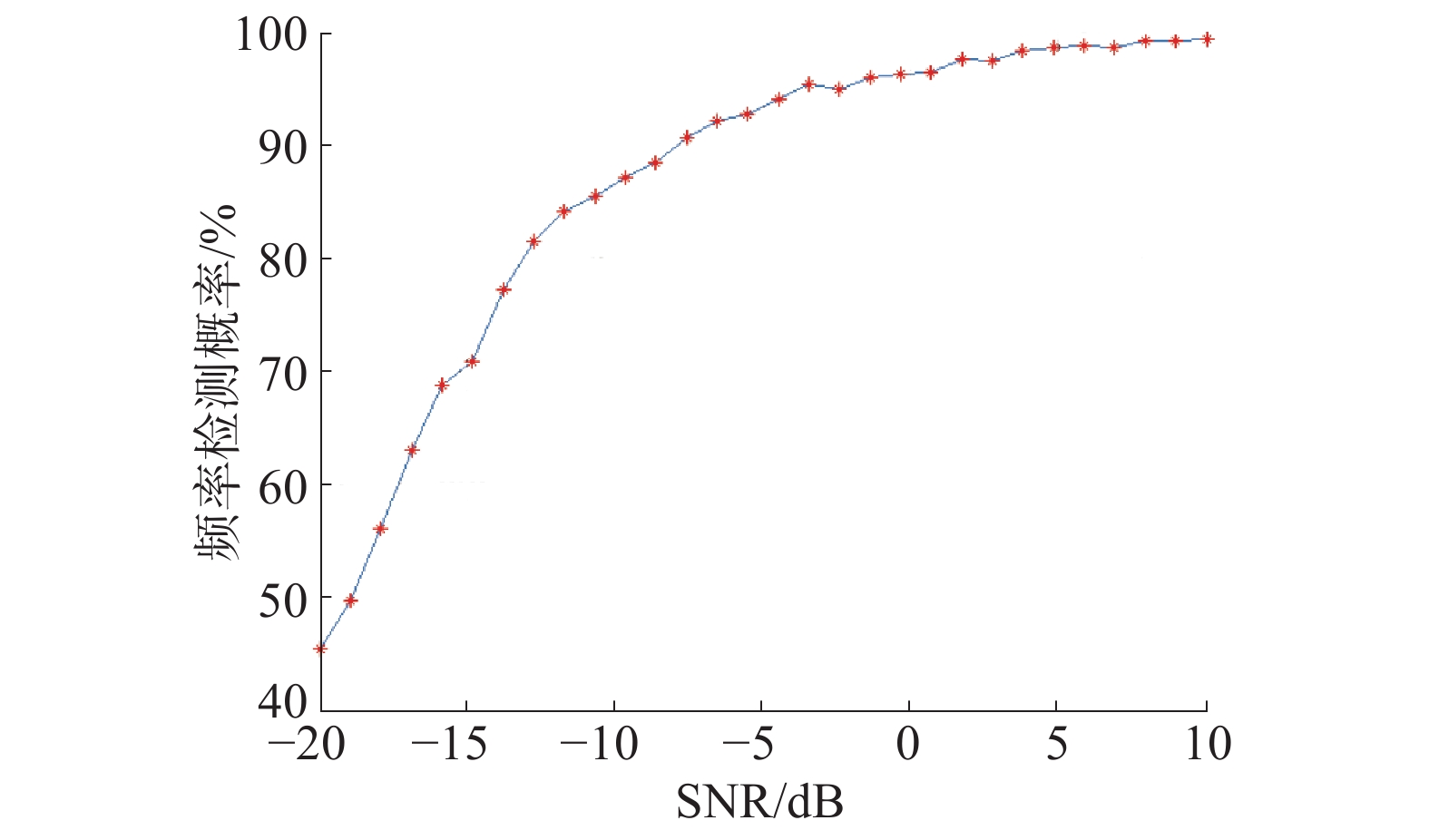
4.1 仿真实验1
在时域欠采样的条件下,单独对多信号的频率估计的顽健性、抗噪声性能进行考察。在该仿真中,固定3个信号的入射角均为38°,设信号的频率
${f_i},i = 1,2,3$
,在1 5002~2 150 MHz内随机选取。若频率估计值
$\left| {{{\tilde f}_i} - {f_i}} \right| < {\rm{30}}\; {\rm{kHz}}$
,即可认为检测成功;否则为检测失败。检测概率随SNR变化的仿真曲线如图2所示,在信噪比大于−7 dB后,检测概率均能达到90%以上,可以看出该算法有着较好的顽健性。
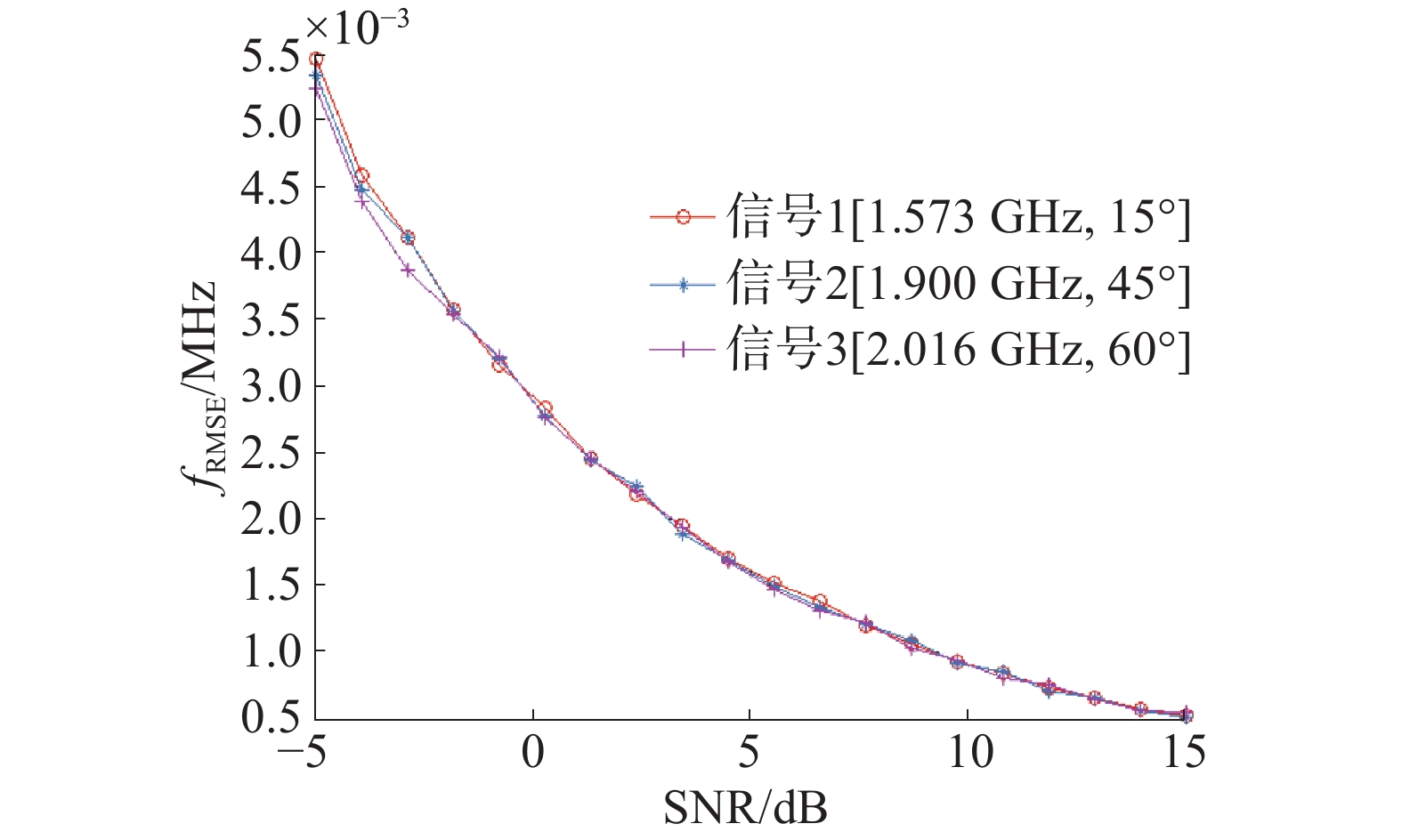
4.2 仿真实验2
接下来验证多个信号的频率、DOA联合估计算法的精度性能。该仿真中,固定3个信号频率和入射角度
${S_i}[{f_i},{\theta _i}]$
分别为
${S_1}$
[1 573 MHz, 10°]、
${S_2}$
[1 900 MHz, 21°]、
${S_3}$
[2 016 MHz, 33°],且同时到达阵列,基于AM估计器的频率估计的RMSE仿真曲线如图3所示。从图3可以看出,本文提出的基于多整数估计CRT的频率估计算法在各个信噪比下均有着较高的精度,当信噪比大于10 dB后,3个信号的频率估计误差均小于1 kHz,即小于信号频率的
$\dfrac{1}{{1 \times {{10}^6}}}$
。
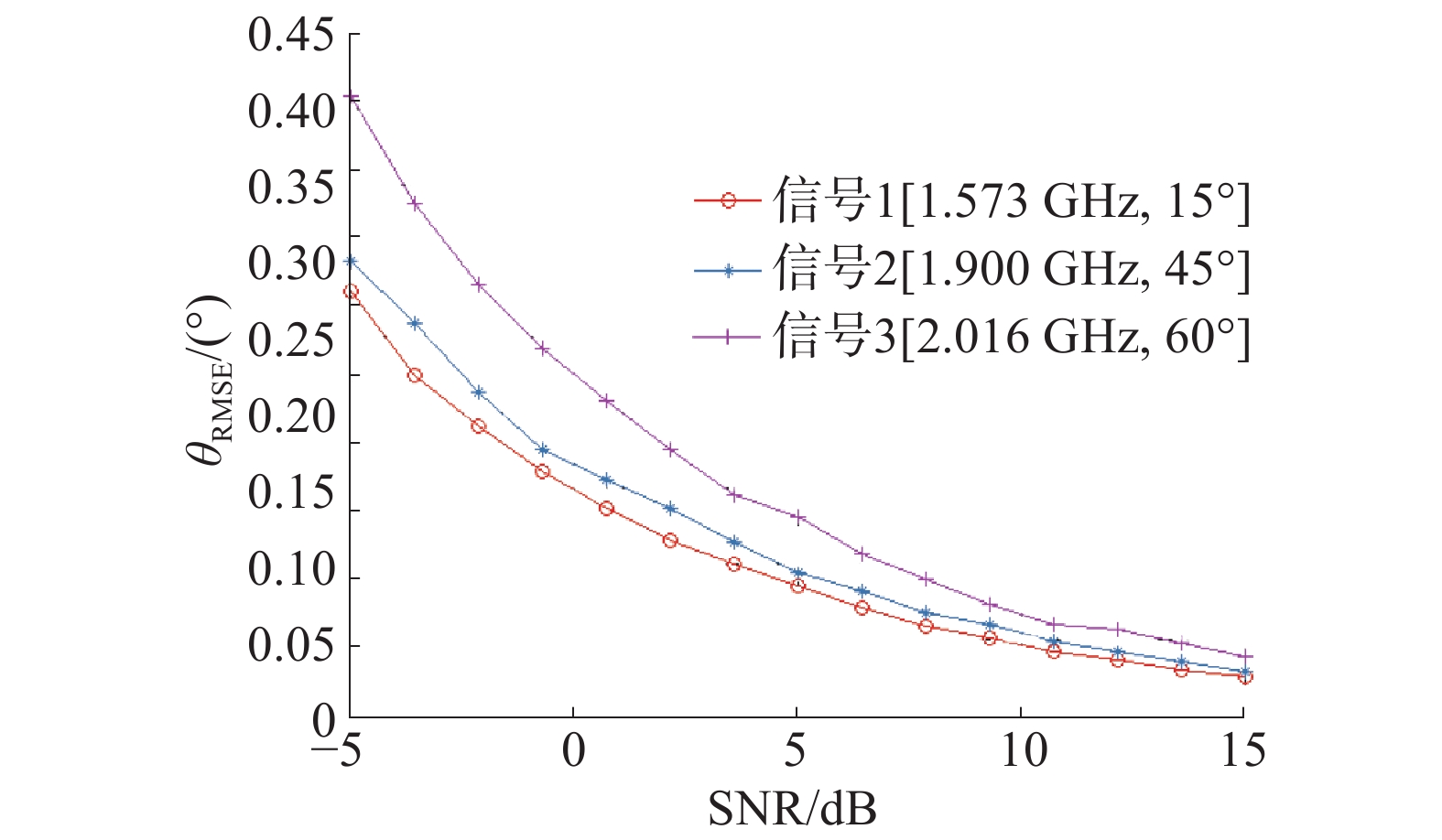
且由于信号频率估计的精确度较高,我们通过频率估计值和ADC采样率可以得到准确的余数,并通过频率估计中谱峰位置得到的余数正确配对同一信号到达4个阵元的初相位。图4为在信号和相位参数配对后,基于闭式CRT算法分别对3个信号的DOA估计的RMSE曲线。可以看出,在各个信噪比条件下均表现出较高的DOA估计精度,并且在(0, 90°]测角范围内,信号入射角度越大,DOA估计误差越大,与理论DOA估计误差一致。
4.3 仿真实验3
考察频率和DOA联合估计时,DOA估计的顽健性和抗噪声性能。在该仿真中,固定3个信号的频率分别为1.573、1.900、2.016 GHz,信号角度在(0, 90°]内随机选取。若DOA估计值
$\left| {{{\tilde \theta }_i} - {\theta _i}} \right| < $
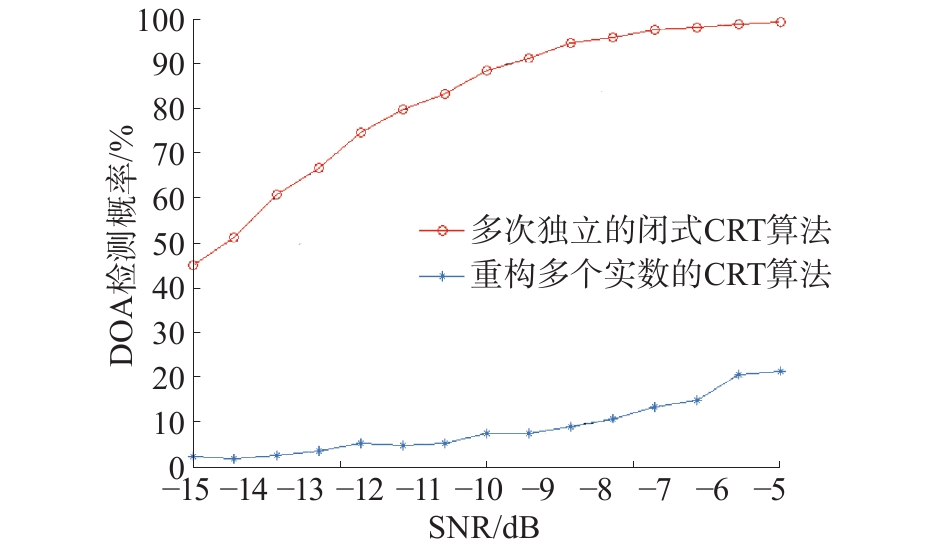
1°,则认为检测成功;否则为检测失败。在DOA估计过程中,采用重构多个整数的CRT和独立3次使用闭式CRT2种算法做比较,得到的检测概率随信号比SNR变化的仿真曲线如图5所示。正如3.2节的讨论,重构多个整数的CRT算法在DOA估计时对允许的相位测量误差的限度较低,其在低信噪比条件下的性能不佳,而在参数配对后单独3次使用闭式CRT算法在信噪比大于−9 dB后,检测概率均能达到90%以上,可以看出其较好的顽健性。
4.4 仿真实验4
最后对比基于MUSIC的空时二维谱频率和DOA联合估计算法的性能和算法耗时。与仿真2相同,固定3个信号频率和入射角度
${S_i}[{f_i},{\theta _i}]$
分别为
${S_1}$
[1 573 MHz, 10°]、
${S_2}$
[1 900 MHz, 21°]、
${S_3}[2\;016 \;{\rm{MHz}},$
33°],且同时到达阵列。对于空时二维谱算法,阵列阵元间距保持不变,4个阵元的采样速率均为650 MHz,满足时域和空域为欠采样的条件。角度在(0, 90°]的范围内以0.1°为步长,频率在
$\left( {{\rm{1}}\;{\rm{500}} \;{\rm{MHz,2}}\;{\rm{150}} \;{\rm{MHz}}} \right]$
以
$0.{\rm{1}} \;{\rm{MHz}}$
为步长搜索得到二维谱如图6所示。
可以看出由于时域和空域的欠采样,空间二维谱会出现伪峰,无法对3个入射信号进行正确的频率和DOA估计。且基于MUSIC的空时二维谱的估计算法的仿真时间为71.985 s,并且会随着搜索步长的减小而增大。而本文提出的时−空欠采样下的频率和DOA联合估计算法的仿真时间为0.037 s,极大地减少了算法运算时间,适合快速时变的工作场景。
5 结论
本文提出了一种在时−空欠采样条件下,能够对多个入射信号进行频率和DOA联合估计的算法,并且给出了对应的阵列模型及算法过程。
1)解决了频率估计时,多组频率余数与多个待估计信号频率对应关系未知情况下,CRT算法失效的问题;
2)解决了多个信号频率值与信号到达阵列初相位的参数配对问题,使得在多信号DOA估计过程中,可以独立多次地使用CRT算法进行单个信号DOA的估计,保证了其顽健性与精确度。
本文提出的算法只需对各个阵元做一次并行欠采样,即可完成频率和DOA的联合估计,有着低运算量和高估计精度的优点,适合雷达、电子战、无线通信等对测量实时性,测量精度有要求等工作场合,具有较广泛的应用场景。

 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2019, Vol. 46
2019, Vol. 46


