随着微波能应用和发展，复介电常数在工业、医学、科学研究中有着越来越重要的意义^[1−3]。复介电常数包含实部和虚部2部分，近年来众多学者对这2个参数的准确测量进行了广泛的研究。现有研究中利用微带线、共面波导、带状线等结构进行复介电常数测量的设计有很多^[4−5]。文献[6]提出一种利用矩形基片集成波导谐振腔测量液体C波段复介电常数的方法，实部和虚部相对误差分别为5%和7%，复介电常数的反演过程使用了人工神经网络。文献^[7]提到一种利用微带线谐振法测量液体S波段复介电常数的方法，介电常数实部和虚部相对误差分别为4.4%和8.6%，反演使用了牛顿迭代法。2种方法具有较高的测量精度，但都只能用于单一频段测量。

在微波工程设计中双频、多频器件的设计一直是个热点^[1]，同时部分物质的介电常数在不同频率时有较大差别。因此，研究多频点复介电常数的高精度测量就非常有必要。本文提出了一种基于基片集成波导结构S和C波段的复介电常数测量系统，待测物通过传感器表面的缝隙直接影响腔体的谐振频率和品质因数。我们使用电磁仿真软件和二元混合液模型，完成对人工神经网络的训练。利用矢量网络分析仪实际测量得到的传感器谐振频率和品质因数，使用训练好的神经网络获得目标频率下介质的复介电常数。

1 传感器原理与测量方法 1.1 基片集成波导谐振原理及分析

基片集成波导（substrate integrated waveguide，SIW）最早于1994年提出^[8]，广泛应用于各种微波器件，包括滤波器、天线、耦合器、传输结构、功率分配器等^[9−10]。该结构是由介质基片的上下金属层和两排间隔一定距离的金属化过孔构成。金属化过孔的相邻间隔远小于波长，等效为理想金属壁。

本文中的传感器主要由2个对角线级联的SIW矩形谐振腔构成，在工作频率下分别谐振于各自的TE₁₀₁模式。类似于矩形波导谐振腔，模式为TE_mnp的SIW谐振腔的谐振频率计算公式如下^[11]：

$ f_{{\rm{mnp}}}^{{\rm{SIW}}} = \frac{1}{{2{\rm{\text π}}\sqrt {\varepsilon \mu } }}\sqrt {{{\left( {\frac{{m{\rm{\text π}}}}{{{L_{{\rm{eff}}}}}}} \right)}^2} + {{\left( {\frac{{n{\rm{\text π}}}}{h}} \right)}^2} + {{\left( {\frac{{p{\rm{\text π}}}}{{{W_{{\rm{eff}}}}}}} \right)}^2}} $

(1)

式中：m=1,2,···；n =1,2,···；p=1,2,···；μ=μ₀μ_r、ε=ε₀ε_r分别表示介质基板的介电常数和磁导率；h为基板的厚度；等效宽度W_eff和等效长度L_eff分别为^[12]：

$ {W_{{\rm{eff}}}} = {W_{{\rm{SIW}}}} - 1.08\frac{{{D^2}}}{{{S_{{\rm{VP}}}}}} + 0.1\frac{{{D^2}}}{{{W_{{\text{SIW}}}}}} $

$ {L_{{\rm{eff}}}} = {L_{{\rm{SIW}}}} - 1.08\frac{{{D^2}}}{{{S_{{\rm{VP}}}}}} + 0.1\frac{{{D^2}}}{{{L_{{\rm{SIW}}}}}} $

式中：D为金属化过孔直径，S_VP为过孔之间的周期距离，W_SIW和L_SIW分别为SIW腔体的实际宽度和长度。依据文献[12]中的计算公式，SIW谐振腔空载品质因数Q_u受到Q_c和Q_d的影响：

$\frac{1}{{{Q_u}}} = \frac{1}{{{Q_c}}} + \frac{1}{{{Q_d}}}$

(2)

式中：Q_c表示无介质损耗时谐振器的品质因数；Q_d表示无欧姆损耗时谐振器的品质因数。Q_d与损耗角正切之间的关系为：

${Q_d} = \frac{{\varepsilon '}}{{\varepsilon ''}} = \frac{1}{{\tan\; \delta }}$

(3)

式中 $\varepsilon '$ 、 $\varepsilon ''$ 分别表示基板介电常数的实部和虚部。

根据腔体微扰法，引入介质微扰将会使得谐振腔的谐振频率和品质因数发生变化^[11]。其介电常数将会使式(1)中SIW谐振腔的等效介电常数ε发生变化并影响谐振频率；式(2)、(3)中谐振器的Q_d和Q_u也会受到影响。待测物介电常数ε与腔体的谐振频率和品质因数的关系通常难以直接求解。

1.2 传感器仿真及测试

本设计中的传感器结构如图1所示。

介质基板选用F4B−2，厚度1 mm，传感器的几何参数如下：50 Ω微带线宽度为2.88 mm；腔体1边长 ${W_{{\rm{SI}}{{\rm{W}}_1}}}$ = 55.2 mm，腔体2边长 ${W_{{\rm{SI}}{{\rm{W}}_2}}}$ =23.6 mm，2个腔体都是正方形腔体；缝隙位于各自正方形腔体的对角线中间，长度分别为 ${L_{{\rm{Slo}}{{\rm{t}}_1}}}$ =20 mm， ${L_{{\rm{Slo}}{{\rm{t}}_2}}}$ =10 mm,宽度为各自长度的14%；金属化过孔直径D为0.8 mm；过孔周期S_vp为1.2 mm。整个传感器尺寸为128 mm × 88 mm × 1 mm，表面镀铜层厚度为17 μm。腔体1谐振频率为2.45 GHz，腔体2谐振频率为5.85 GHz，2个腔体之间的馈电耦合结构使得传感器能够在2个谐振频点都取得较好的谐振效果。采用50 Ω微带线与外部电路连接，通过仿真优化提高腔体的品质因数并减少输入端的反射。结合电磁仿真软件分析，传感器腔体在2.45 GHz和5.85 GHz的谐振模式和场强分布，如图2所示。

2条缝隙位于传感器的对角线上每个腔体中心位置，长度分别接近于工作频率下的四分之一波导波长。随着待测物介电常数的变化，传感器的谐振频点和品质因数都会随之变化。图3是传感器的实物以及介电常数测量系统，传感器表面的矩形方框是附加测试槽，它使得液体类待测物能够始终保持在腔体的电场最强处，并保证每次测量的用量一致，根据理论分析和实验验证表明附加测试槽对腔体的谐振结构不产生影响。

表1中为仿真与实测腔体的谐振频率和品质因数Q对比，从数据中看出仿真结果与实测结果吻合良好。

2 神经网络反演系统及反演结果 2.1 神经网络反演系统

人工神经网络（artificial neural network，ANN）是一种模仿人类大脑中神经突触联结的结构来处理信息的数学模型，是一种自适应系统，能够根据外界信息改变内部联系强度和传递规则^[13]。

现阶段对于介电常数双频测量难以获得准确的公式。因此，利用人工神经网络反演系统作为数据关系重构工具。重构过程中调节传输函数和加权因子，采用大量数据训练神经网络。当训练误差小于设定目标后，完成训练过程，得到能够直接构建传感器品质因素和谐振频点与介电常数之间的神经网络系统。利用神经网络重构数据关系，实现较高的复介电常数重构精度。

2.2 复介电常数反演过程和结果

由于独特的结构设计，这个传感器在2个工作频点都具有较高的品质因数，使得其有一个较宽的测量范围和测试精度。本工作的关键点在于重构提取出来的品质因数和谐振频率与待测液体的复介电常数的关系。通过对测量数据中的S波段参数进行处理，得到传感器的品质因数和谐振频点。

为了确定传感器的测量精度和范围，我们采用了乙醇与水混合二元溶液作为待测液体。该混合溶液有较宽的介电常数范围，配制简单易得。在20 ℃下配制了乙醇浓度从0~100%均匀变化的溶液11份。在测试槽内满载待测液体，使用矢量网络分析仪测量传感器的|S₁₁|，并计算谐振频率和品质因数。由于温度对复介电常数影响较大，整个测试过程中尽量保持温度一致。

采用神经网络进行介电常数的反演。首先进行神经网络的训练。将加载了不同介电常数的传感器进行电磁仿真，获得相应的谐振频率和品质因数；再将这些数据作为神经网络的输入层数据，介电常数实部和虚部作为输出层的数据；然后在训练过程中不断调节隐藏层的神经元数目以及传递函数，直到训练误差收敛时完成训练；最后保存训练好的神经网络，将传感器实际测量乙醇混合溶液得到的谐振频率和品质因数输入到神经网络，就可以获得待测溶液的介电常数。

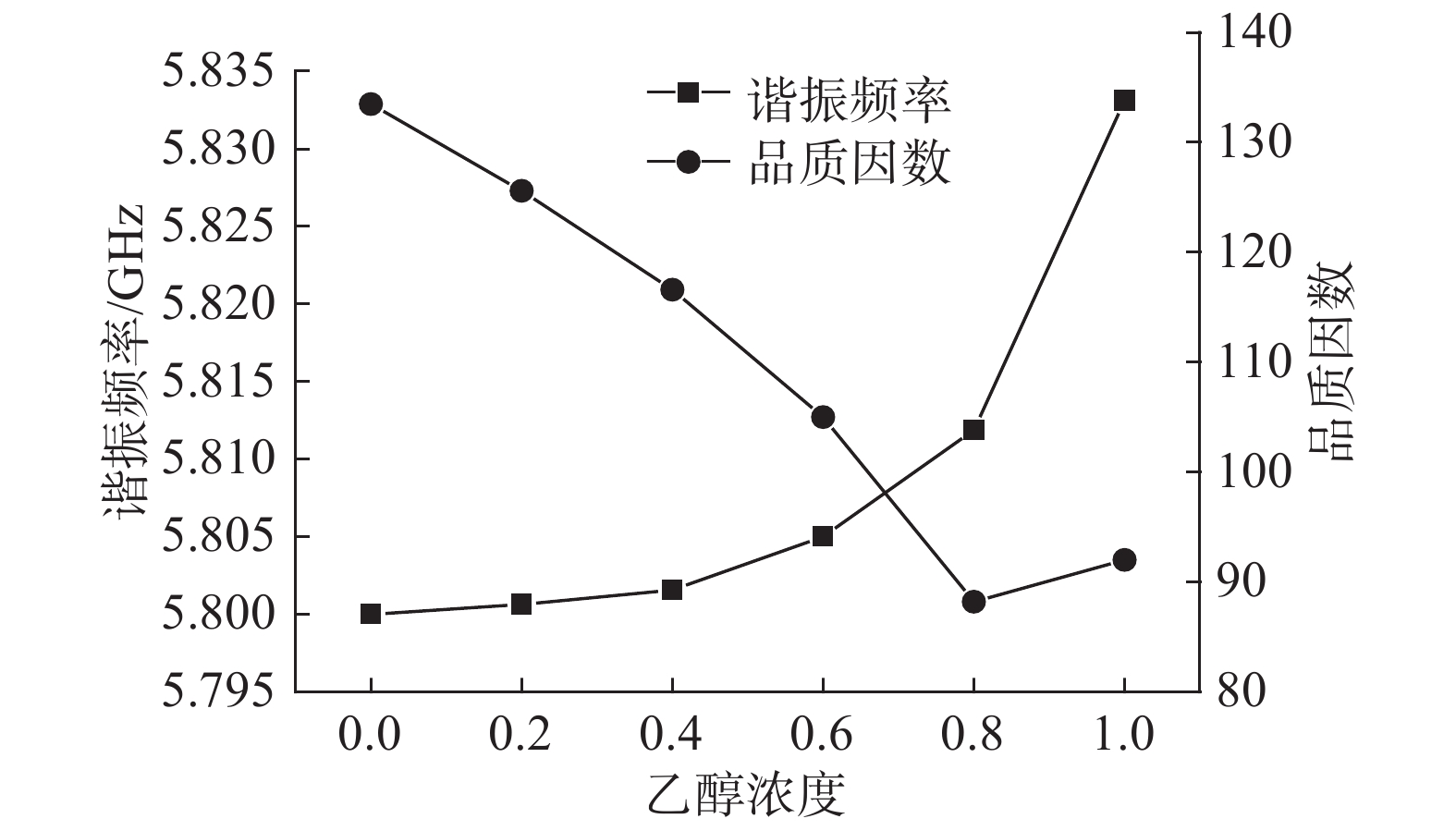
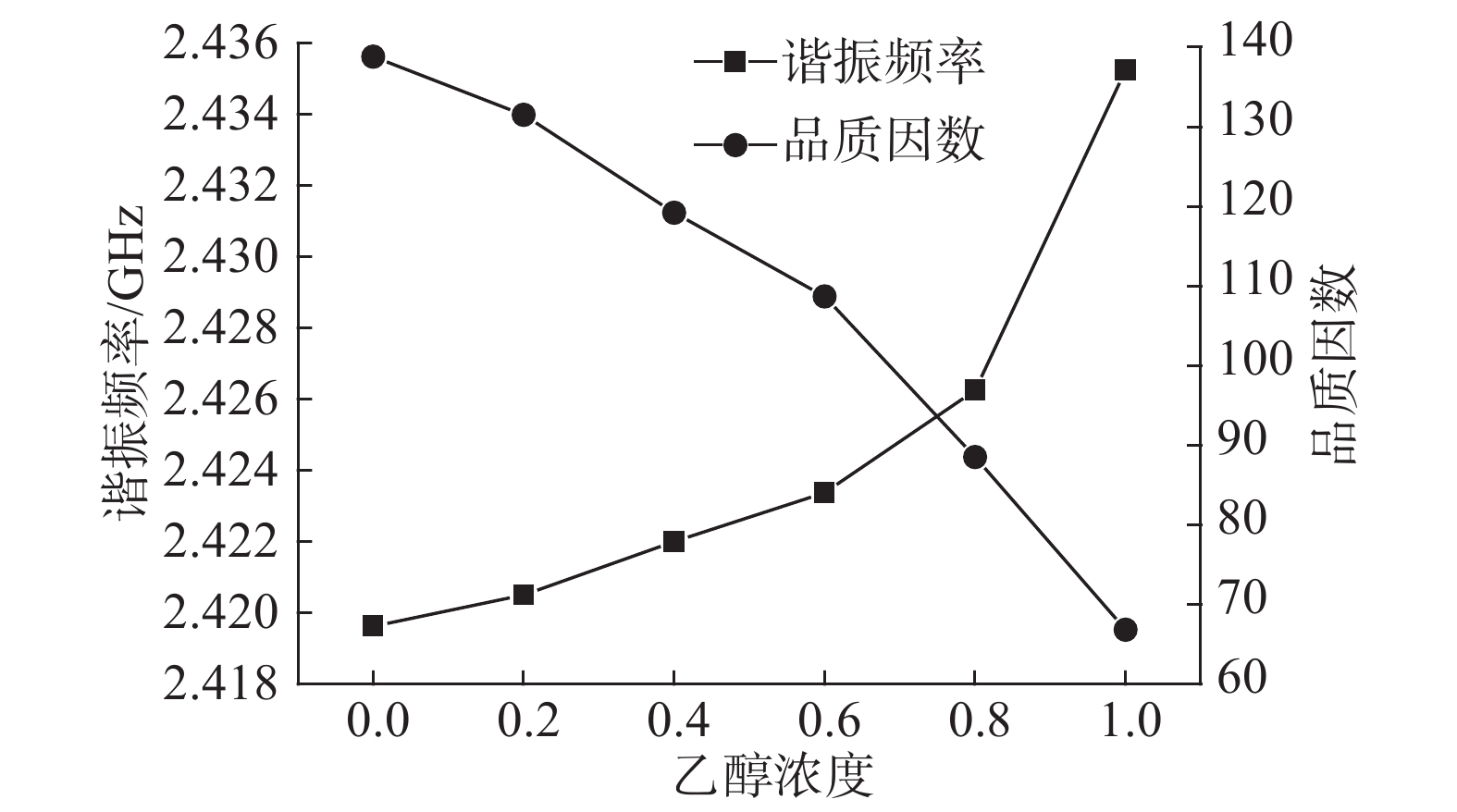
本设计中，传感器测试样本的谐振频率和品质因数结果如图4、5所示，图4为S波段测试结果，图5为C波段测试结果，谐振频率与品质因数变化明显，在不同频段有明显特点。

测试数据经过神经网络反演后得到的复介电常数与理论值^[14]计算相对误差，在2.45 GHz时测试结果的最大误差分别为1.98%和1.28%，5.85 GHz时为2.51%和2.68%，整个范围内吻合良好。

3 结论

1）提出一种可用于S和C波段的介电常数测量系统，经过加工测试，仿真与实测数据吻合良好；

2）在介电常数反演过程中，成功利用人工神经网络技术加速推演过程；

3）利用乙醇与水混合二元溶液进行测量系统精度验证，介电常数实部和虚部的相对误差在2.45 GHz分别为1.98%和1.28%，5.85 GHz分别为2.51%和2.68%。

该介电常数测量系统中的传感器易于其他平面电路和射频系统，具有双频工作和易于加工的特性，可推广用于工业应用中介电常数的在线测量。