医学影像处理是多模态图像处理中的一个重要分支，在医学成像技术中，不同成像设备下的医学影像呈现出不同模态，如计算机断层成像（CT）、磁共振成像（MRI）、正电子发射断层成像（PET）等^[1]。不同模态提供了不同的人体组织信息，单一模态的医学影像无法为放疗医生提供足够的病灶信息，因此往往需要将不同模态的影像信息进行综合处理。医学影像配准是医学影像融合的先决条件，由于医学影像受成像时间、成像设备、患者姿势等因素的影响，多模态影像之间难以在空间位置上配准^[2]。在配准的基础上，为了能够更加全面、可靠地反映人体各组织器官以及病灶部位的信息，需要对多模态医学影像进行高效的融合处理。

在配准过程中，用作参考的影像为固定影像，进行变换的影像为浮动影像。医学影像配准的过程就是为浮动影像寻找一个最佳变换，使之与固定影像达到空间上的匹配。人体内部组织结构复杂且具有时变特性，例如肺部扫描影像中的组织器官会随着患者的呼吸而位移，因此刚体配准无法满足要求，需要选择合适的变换对医学影像进行复杂的非刚体配准；同时，不同模态的医学影像难以提取共同特征，因此无法基于特征来评价影像之间的配准程度。医学影像的融合不仅仅是影像之间的简单叠加，而需要考虑不同影像间冗余信息的处理以及互补信息的最大化保留，并通过一系列指标来评价融合影像的信息丰富程度。在多模态医学影像融合方法的选择上，多分辨率的融合方法能分别处理不同尺度下的细节信息，但需要分别选择侧重影像概貌或细节信息的融合规则。

本文以互信息为相似性测度，搭建仿射变换与B样条变换相结合的多层次配准框架，实现多模态医学影像的非刚体配准。同时，对配准后的影像按不同融合规则进行基于小波变换的多分辨率融合，实现多模态医学影像重要信息的高效集成。

1 多模态医学影像非刚体配准方法 1.1 医学影像配准框架

通常医学影像配准主要包括了空间变换、插值方法、优化算法与相似性测度4个部分。其中相似性测度用来描述固定影像与浮动影像之间的配准程度；优化算法根据相似性测度对变换参数进行优化；空间变换部分将优化后的变换参数作用于浮动影像，并通过特定的插值方法形成新的影像^[3]。通过不断迭代直到相似性测度达到配准要求。通常由于医学影像的特殊性，医学影像配准是非常耗时的过程，也是制约医学影像应用的重要因素之一。提高医学影像配准精度始终是医学影像处理的重要内容。

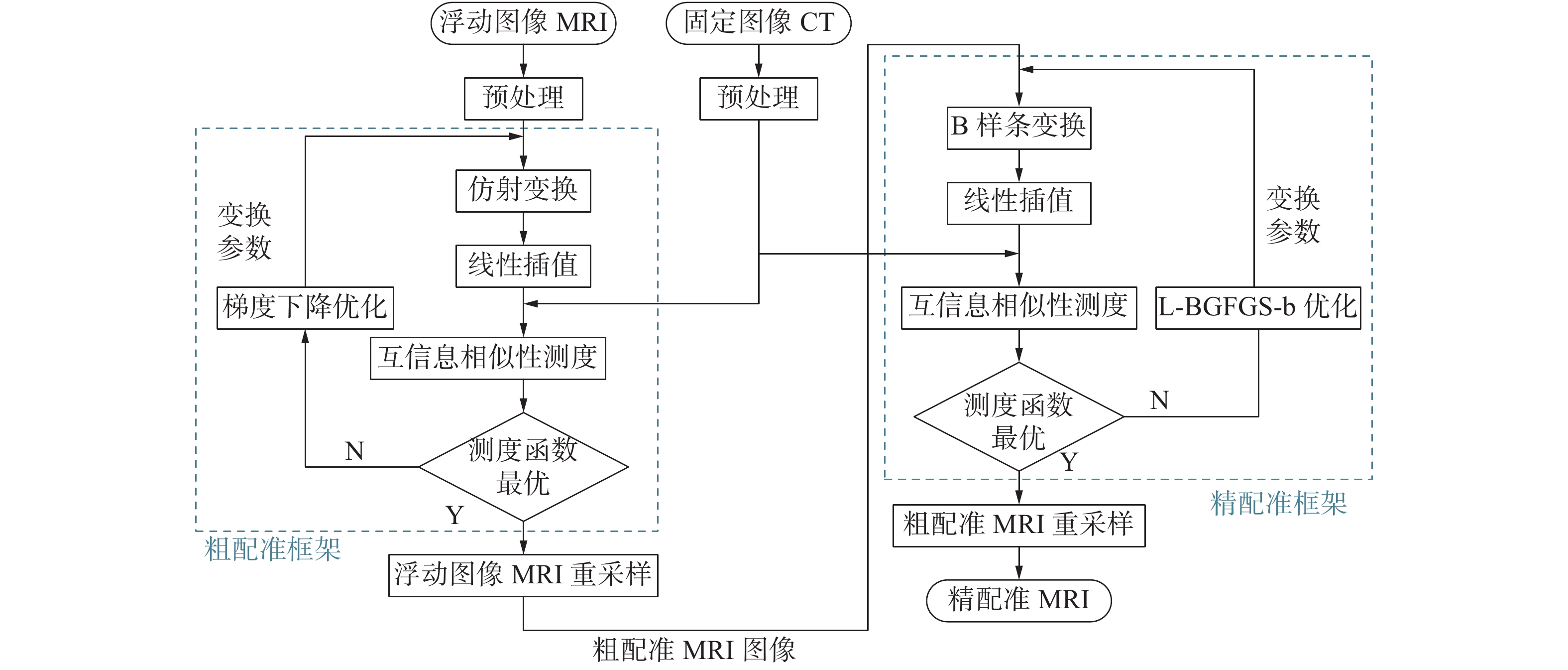
以上述思想为基础，本文提出了粗配准与精配准相结合的配准方法。其中粗配准通过仿射变换使固定影像与浮动影像在较少的迭代次数中达到大小和位置上的近似匹配；精配准通过B样条变换在粗配准的基础上对浮动影像进行复杂形变，使2幅影像达到细节上的高精度匹配。粗配准与精配准均选择基于影像自身灰度信息的互信息测度作为相似性测度，因此不需要考虑特征提取。图1是本文的配准流程图。

1.2 粗配准方法 1.2.1 多模态影像配准下相似性测度方法

相似性测度是医学影像配准中的关键部分。在多模态医学影像配准问题中往往更侧重于考虑影像本身灰度信息的关联，而不考虑影像之间的特征提取问题。互信息是基本信息度量方法，用于度量2个事件集合之间的相关性，即一个事件集合中包含另一个事件集合信息的程度^[4]。互信息测度是一种基于影像像素灰度的测度方法，适用于多模态下影像的配准，是目前得到广泛研究和应用的方法^[5]。

若将2幅影像看作为2个事件集合，影像之间的配准程度越好，2幅影像的相关性越大，互信息值越大。假设固定影像与浮动影像分别为A和B，则2幅图的互信息I（A，B）计算方法如式为：

$ \begin{array}{l} I\left( {A,B} \right) = H\left( B \right) - H\left( {B\left| A \right.} \right) = H\left( A \right) + H\left( B \right) - H\left( {A,B} \right) \end{array} $

式中： $H\left( A \right)$ 、 $H\left( B \right)$ 分别为影像A和影像B的信息熵； $H\left( {B\left| A \right.} \right)$ 是两幅影像的条件信息熵； $H\left( {A,B} \right)$ 为联合信息熵，它们定义为：

$ \left\{ \begin{aligned} & H\left( A \right) = - \sum\limits_a {{p_A}\left( a \right)\log {p_A}\left( a \right)} \\ & H\left( B \right) = - \sum\limits_b {{p_B}\left( b \right)\log {p_B}\left( b \right)} \\ & H\left( {A,B} \right) = - \sum\limits_{a,b} {{p_{A,B}}\left( {a,b} \right)\log {p_{A,B}}\left( {a,b} \right)} \end{aligned}\right. $

式中： ${p_A}\left( a \right)$ 表示影像A中灰度值为a的概率； ${p_B}\left( b \right)$ 表示影像B中灰度值为b的概率； ${p_{A,B}}\left( {a,b} \right)$ 表示影像A和影像B在对应位置灰度值分别为a和b的概率值。

1.2.2 粗配准变换方法

当固定影像与浮动影像的大小、位置相差较大时，直接对影像进行复杂形变的非刚体配准的变换操作时不仅配准效果不理想，而且会消耗大量迭代时间。仿射变换主要作用是对影像进行旋转、平移与缩放，它可以分解为线性（矩阵）变换和平移变换^[6]。通过仿射变换对影像进行粗配准，可以使影像的大小与位置达到近似匹配。二维空间里的仿射变换数学公式定义为：

$ \left( {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ {z'} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} a&b&{{t_x}}\\ c&d&{{t_y}}\\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right) $

(1)

式中： $\left( {a,b,c,d} \right)$ 为仿射变换的参数； $\left( {{t_x},{t_y}} \right)$ 为位移参数。

1.2.3 粗配准结果分析

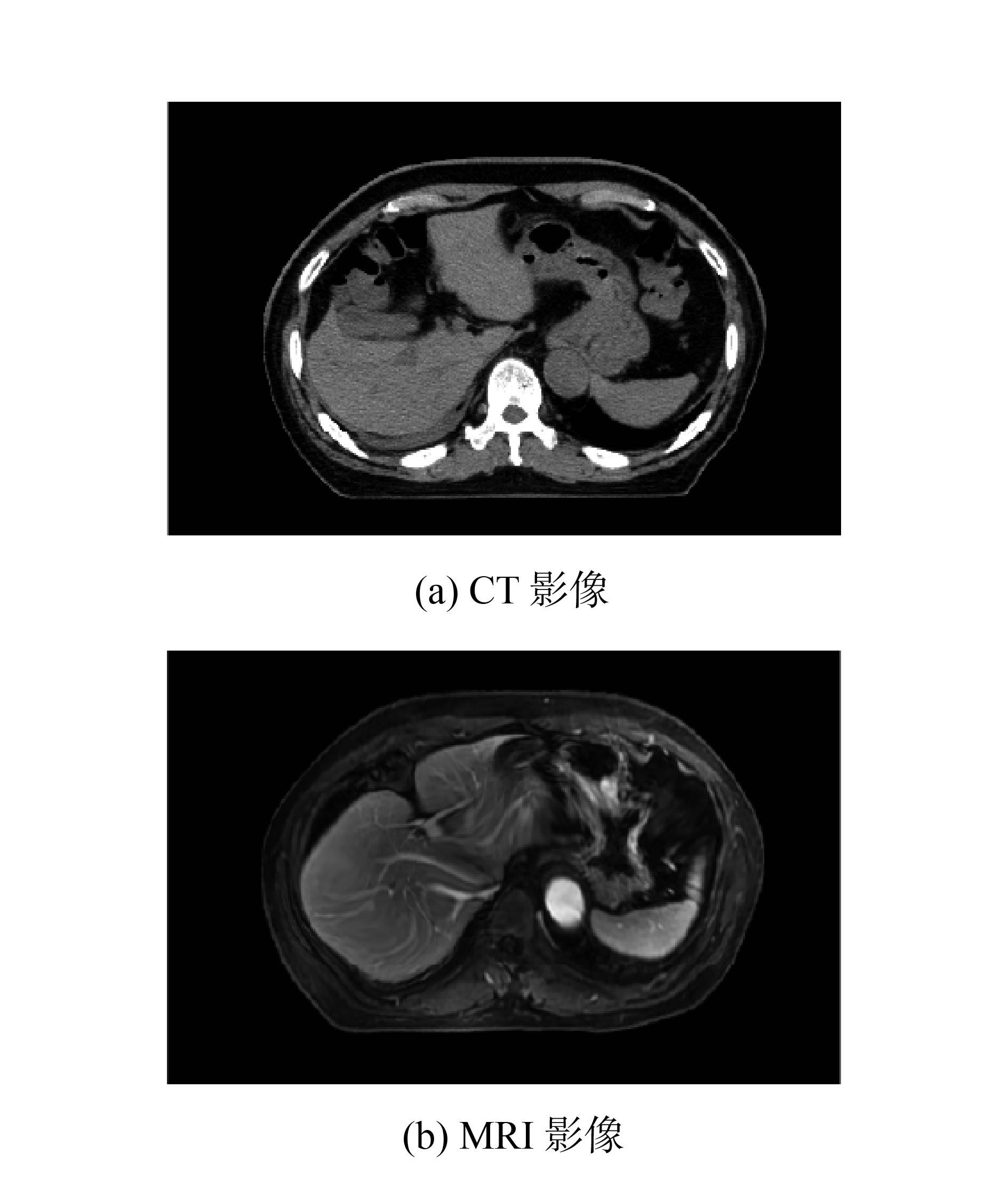
为了检验粗配准的有效性，本文使用的CT、MRI实验数据来自北京陆军总医院放射治疗科，多模态医学影像配准部分在Visual Studio 2015平台下利用ITK工具包实现，选取CT影像为固定影像，MRI影像为浮动影像，其中固定影像CT与浮动影像MRI的分辨率均为512×512。如图2所示，可看出2幅影像灰度分布不同，且腹部区域的大小和形态均有较大差别。

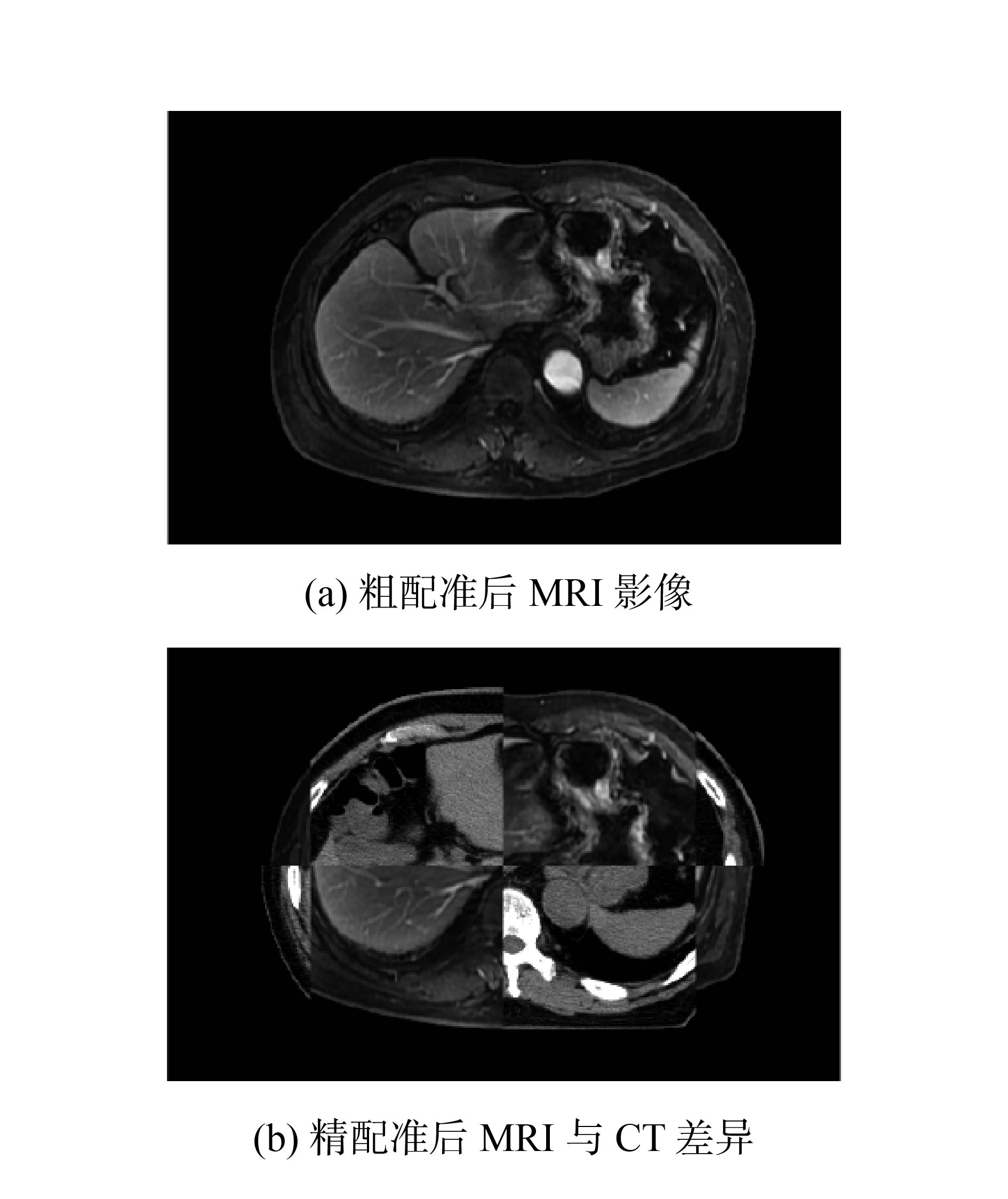
粗配准框架下配准结果如图3所示。从配准结果可看出，经过刚体配准后，MRI影像的大小与位置已经与CT影像达到近似配准，但2幅影像的轮廓与内部组织依然存在一定差异，图3（b）棋盘图像中右下角部分能看到明显的错位。

图4是粗配准过程中的互信息变化曲线。在前10次迭代中，由于2幅影像差异很大，经仿射变换可看出互信息明显上升；11~17次迭代中不断寻找最佳变换参数，互信息曲线上下波动；随后的迭代中，迭代结果不断向最优配准逼近，互信息曲线趋于稳定。经过40次迭代后，CT影像与MRI影像的互信息由0.10上升到0.38，说明2幅影像之间的相关性增强，与未配准时相比，重叠程度明显上升，影像配准程度变好。

1.3 非刚体配准框架的方法 1.3.1 精配准框架中的变换方法

由于式（1）所示的仿射变换无法对影像进行复杂变换，浮动影像的外部轮廓和内部组织结构仍然无法实现精确配准，这就需要在粗配准的基础上对浮动影像进行非线性形变的非刚体精配准。

在非刚体配准问题中，由于B样条空间变换^[7−8]方法能够模拟生理结构，已经成为非刚体配准中的重要变换模型。B样条变换的主要过程包括设置网格空间、嵌入浮动影像、对网格点变形以及重建变形后的浮动影像。在B样条变换中，变形场可以描述为

$ T(x,y,z) = \sum\limits_{l = 0}^3 {\sum\limits_{m = 0}^3 {\sum\limits_{n = 0}^3 {{B_l}(u){B_m}(v){B_n}(w){\phi _{i + l,j + m,k + n}}} } } $

式中： ${\phi _{i,j,k}}$ 是网格大小为 ${n_x} \times {n_y} \times {n_z}$ 且间隔均匀为 $\delta $ 的一组控制点中的点， $i = \left[ {x/{n_x}} \right] - 1$ ， $j = \left[ {y/{n_y}} \right] - 1$ ， $k = \left[ {z/{n_z}} \right] - 1$ ； $u = x/{n_x} - \left[ {x/{n_x}} \right]$ ； $v = y/{n_y} - \left[ {y/{n_y}} \right]$ ； $w = z/{n_z} - $ $\left[ {z/{n_z}} \right]$ ； ${B_l}$ 表示第l个B样条基函数，定义如下：

$ \left\{ \begin{aligned} & {B_0}(u) = {(1 - u)^3}/6\\ & {B_1}(u) = (3{u^3} - 6{u^2} + 4)/6\\ & {B_2}(u) = ( - 3{u^3} + 3{u^2} + 3u + 1)/6\\ & {B_3}(u) = {u^3}/6 \end{aligned}\right. $

B样条模型的优点在于它对影像操作是局部的，即控制点位置变化只影响控制点邻域的变化，这样配准问题就等价于三次B样条的局部控制问题，从而使B样条计算效率更高，精度也能达到亚像素级^[9]。

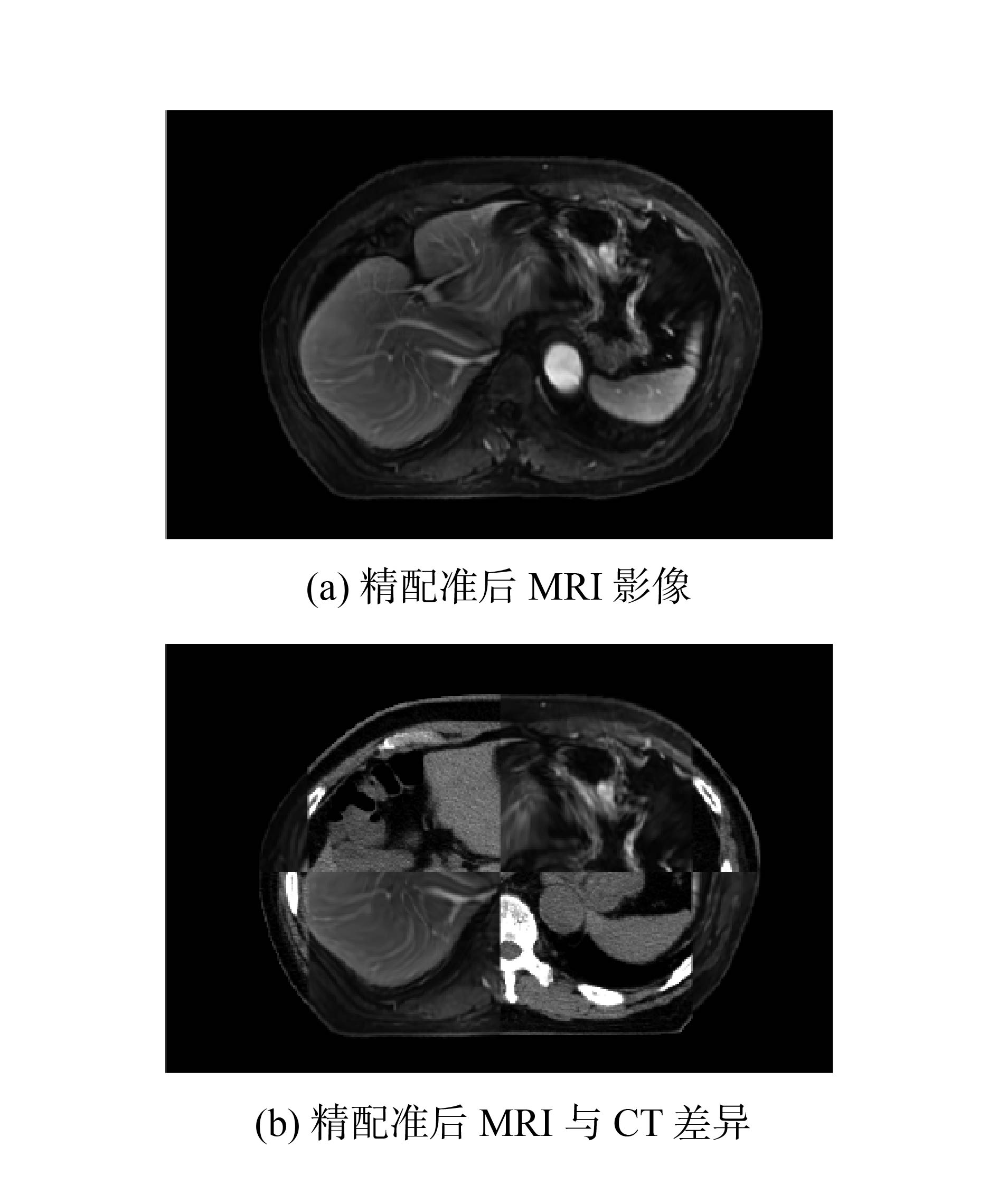
1.3.2 精配准结果分析

精配准框架下配准结果如图5所示。精配准后MRI影像的外部轮廓与内部组织结构与CT影像一一匹配，在棋盘差异图下几乎没有边缘错位，配准效果较好。图6是精配准过程中的互信息变化曲线。

由图6可知，前50次迭代中，由于2幅影像差异较明显，配准程度提高较快，互信息曲线明显上升；在随后的迭代中，迭代结果不断向最优配准逼近，互信息曲线趋于稳定。在粗配准基础上，精配准经过200次迭代后互信息达到0.411，说明精配准进一步提高了影像间的相关性，使配准结果与固定影像达到细节上的匹配，为影像融合打下良好基础。

2 多模态医学影像多分辨率融合方法

将经过预处理后的CT影像与精配准后的MRI影像作为影像融合部分的输入影像。为了利用不同来源医学影像的各自特征，需要对影像进行多源信息融合。本文第1章论述的影像配准为影像融合打下了良好基础，在此基础下，采用基于小波变换的融合方法。

2.1 小波变换融合方法

基于小波变换的影像融合方法是在不同频率分量下进行不同规则的融合处理，可以获得与人眼视觉更接近的融合效果。基于小波变换的影像融合方法^[10]首先对2幅影像分别进行小波分解，将分解后的高频小波系数与低频小波系数分别按一定的规则进行融合，得到融合后的小波系数，并进行小波逆变换得重构后的融合影像^[11]。设I₁和I₂为待融合的2幅影像，则小波融合过程如图7所示。

小波融合过程中的重点在于小波分解与分解后融合规则的选取上^[12]。小波分解形式包括小波基与分解层数的选择，为了提高小波分解效果，本文采用了db3小波并采用二次分解方法；融合规则包括点对点的像素融合以及窗口对窗口的区域融合方法选择，融合规则直接影响融合影像的质量。

2.2 二维小波分解与重构

利用连续小波变换进行计算，计算量非常大，因此要考虑小波变换的快速算法，目前所采用的技术是沿用Mallat快速算法。二维小波分解Mallat快速算法的分解公式为^[13]

$ \left\{ {\begin{aligned} & {{{C}_{j + 1}} = {L}{{C}_j}{{L}^{^*}}}\\ & {{D}_{j + 1}^H = {H}{{C}_j}{{L}^{^*}}}\\ & {{D}_{j + 1}^V = {L}{{C}_j}{{H}^{^*}}}\\ & {{D}_{j + 1}^D = {H}{{C}_j}{{H}^{^*}}} \end{aligned}} \right.\;\;\;\;\;\;j = 0,1, \cdots ,J - 1 $

(2)

式中：j为分解层数；C_i+1为低频分量； ${ D}_{j+1}^H$ 为水平方向上的高频分量； ${ D}_{j+1}^V$ 为垂直方向上的高频分量； ${ D}_{j+1}^D$ 则为对角方向上的高频分量；L为低通滤波算子；H为高通滤波算子； ${ L}^{^*}$ 和 ${ H}^{^*}$ 分别为L和H的共轭转置矩阵。

由式（2）所示的小波系数可以对小波变换进行重构，小波逆变换算法为：

$ {{C}_{j - 1}} = {{L}^{^*}}{{C}_j}{L} + {{H}^{^*}}{D}_j^H{L} + {{L}^{^*}}{D}_j^V{H}{\rm{ + }}{{H}^{^*}}{D}_j^D{H} $

2.3 小波变换融合规则

CT和MRI影像分解后不同频带系数反映的影像信息不同，低频系数融合规则侧重于反映多模影像的共同轮廓特征，高频系数融合规则侧重于反映尽可能多的细节信息。因此对不同频带小波系数需要选取不同的融合规则。

2.3.1 低频系数融合规则

本文采用加权平均方法确定低频子带系数的融合规则，即将影像I₁、I₂分解后的低频小波系数各乘上一个权重因子，按式（3）求出融合后的系数，是基于像素的融合规则。

$ D_F^j\left( {m,n} \right) = {c_1}D_A^j\left( {m,n} \right) + \left( {1 - {c_1}} \right)D_B^j\left( {m,n} \right) $

(3)

式中：j为分解层数； $D_A^j\left( {m,n} \right)$ 与 $D_B^j\left( {m,n} \right)$ 分别表示影像I₁与影像I₂第j层对应 $\left( {m,n} \right)$ 位置处的低频小波系数；c₁为权值系数。

2.3.2 高频系数融合规则

1）绝对值最大法

绝对值最大法是基于像素的融合规则。高频系数在零值上下波动，绝对值越大说明灰度变化越明显。因此如式（4）所示选取对应高频系数中各对应点的最大值，可以得到更多细节信息。

$ D_F^j\left( {m,n} \right){\rm{ = }}\max \left( {\left| {D_A^j\left( {m,n} \right)} \right|,\left| {D_B^j\left( {m,n} \right)} \right|} \right) $

(4)

该方法原理清晰且便于理解，计算效率较高，然而绝对值最大法仅对各系数单独处理，对系数间的关联性考虑不够全面，同时融合结果在对比度上可能有所降低。

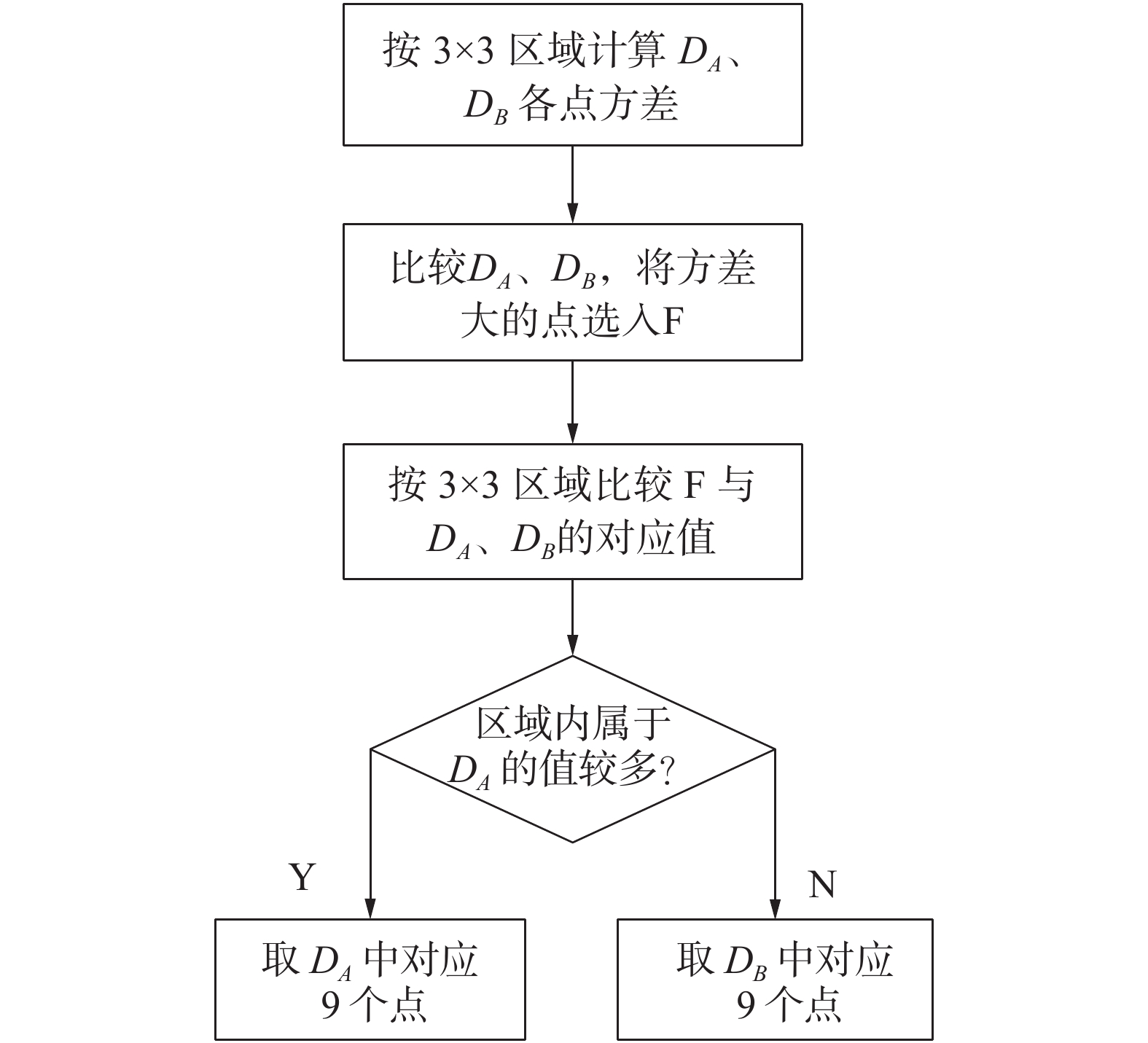
2） 区域方差最大法

区域方差最大法是基于区域的融合规则^[14]。首先计算高频系数中对应 $M \times N$ （本文选择 $3 \times 3$ ）区域下各中心点的区域方差，将方差大的系数点选入新的系数矩阵F中，最后比较F矩阵各区域内来自不同影像高频系数的点的个数，得出最后的融合结果。区域方差最大法具体流程如图8所示。

该方法可以反应影像灰度分布的离散程度，在灰度反差明显的部分能很好地保留源影像的特征信息；然而在灰度分布平缓的区域，区域方差法难以最大化保留源影像的信息，同时该方法计算量较大。

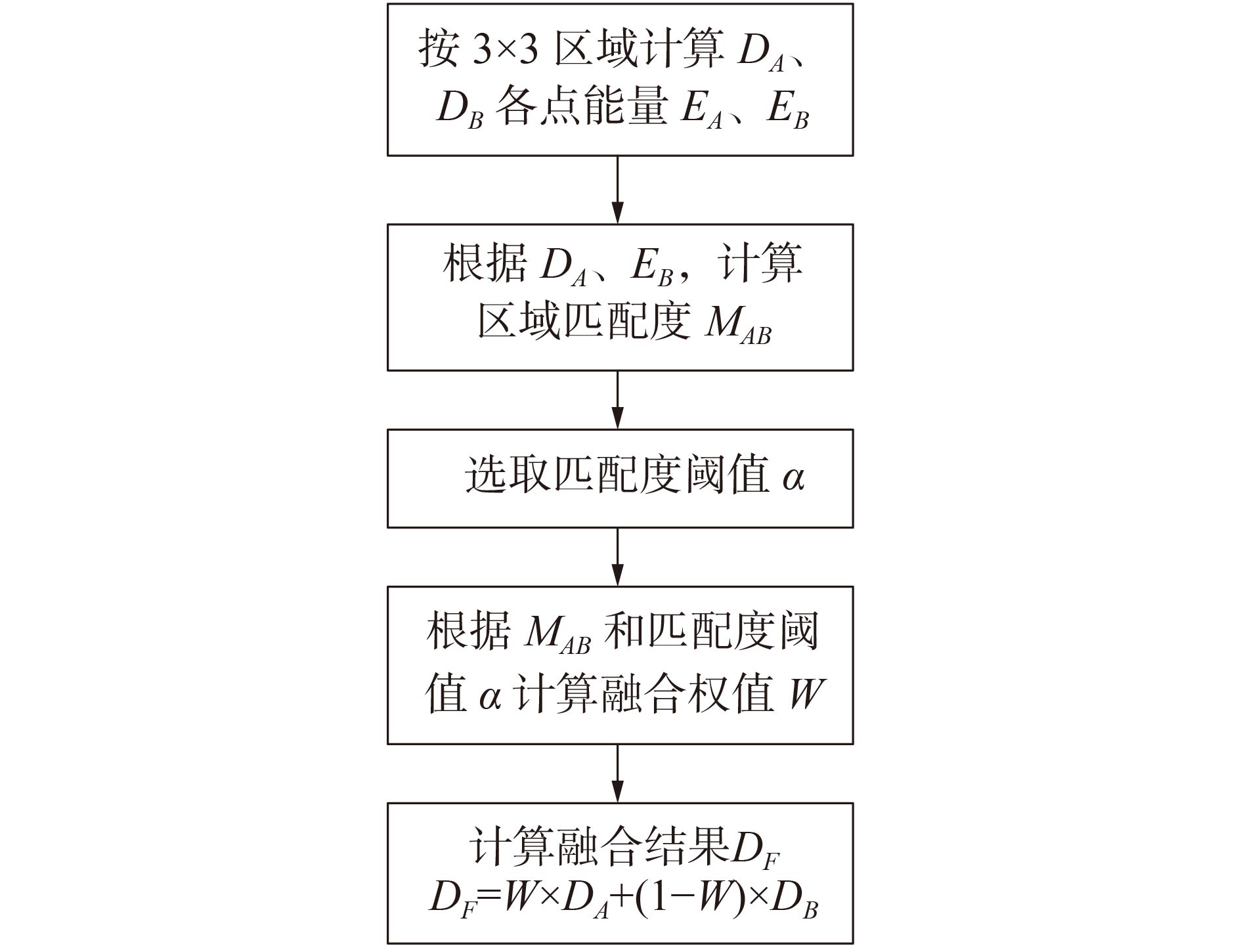
3)区域能量融合法

区域能量融合法是基于像素的融合规则^[15]，但引入了区域能量的概念。首先计算高频系数中对应 $M \times N$ （本文选择 $3 \times 3$ ）区域下各中心点的区域能量，并由此计算区域匹配度，通过区域匹配度与阈值计算区域融合法的权值，最终计算出权值下各点融合结果。区域能量融合法具体流程如图9所示。

区域方差法结合了前两种融合规则的特点，既应用了加权平均的思想，又在确定权重系数时充分考虑了像素之间的关联性；然而该方法容易忽略灰度较低的细节部分，使最终结果中出现失真现象，且计算量大，处理过程耗时长。

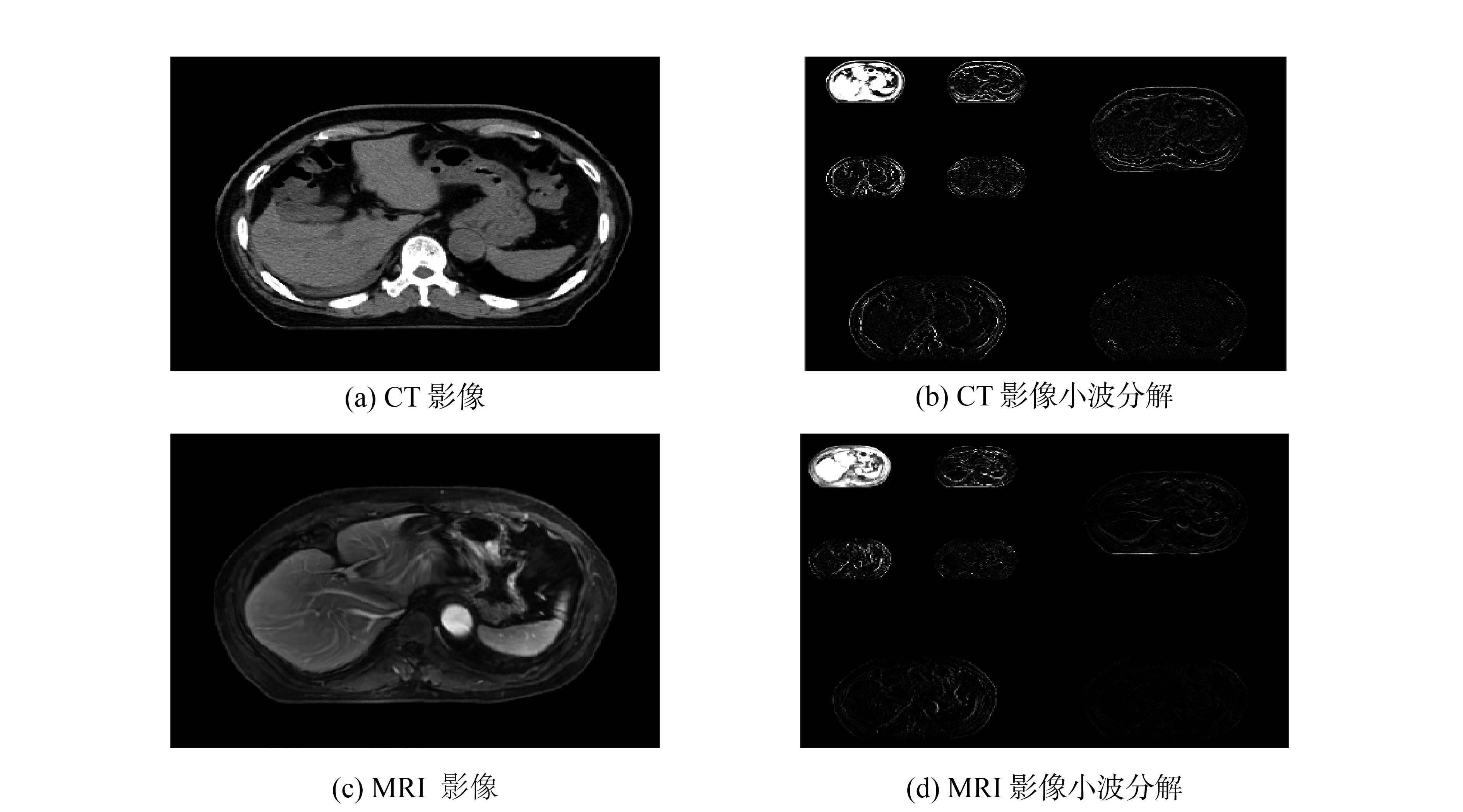
2.4 影像融合结果分析

在MATLAB R2014b平台下实现影像小波分解的Mallat算法，从紧支性、正交性、对称性、消失矩4个方面考虑，选择db3小波作为小波分解与重构的小波基。影像的2层小波分解结果如图10所示，低频系数反映轮廓信息，高频系数反映细节信息。

对分解后CT影像与MRI影像的小波系数进行融合处理，在融合规则选取上，对低频系数进行加权平均融合，对高频系数采用上述绝对值最大、区域方差最大、区域能量融合3种方法进行融合。图11是多源影像融合结果，从3幅影像中可看出，融合后的胸腹腔不仅显示出了CT影像中的骨骼结构，也显示出了MRI影像中的血管、软组织等细节，最关键的是肿瘤区域轮廓明显、亮度增加，更利于放疗医生进行病灶识别。

为了客观地比较不同方法的融合结果，本文利用均值、信息熵、标准差、清晰度、空间频率^[16]5个指标进行评价，结果如表1所示。可以看出，不同评价方法在不同指标下所得的评价值有各自的优势，有经验的医师可以根据不同的评价指标选择最合适的融合方法。本文所提融合算法已在多组CT与MRI断层扫描影像序列下进行了有效性验证。

3 结论

本文主要讨论了多模态医学影像的非刚体配准与多分辨率融合方法。

1)在影像配准部分采用基于仿射变换的粗配准与基于B样条变换的精配准相结合的非刚体配准方法，并用互信息测度评价配准程度，提高了配准的精度与计算速度。

2)在影像融合部分，提出在不同频带使用不同融合规则的基于小波变换的多分辨率融合方法，对低频系数进行加权平均融合，对高频系数分别采用绝对值最大法、区域方差最大法、区域能量融合法进行融合，融合结果最大限度地保留了多模态医学影像的有效信息。

本文使用腹部CT影像与MRI影像验证了所提配准与融合方法的有效性。本文工作是未来实现多模态医学影像的三维重构、三维配准融合以及三维靶区勾画的重要基础。上述方法还可以广泛应用于其他多源图像配准与融合，例如多源遥感图像。