压缩感知(compressive sensing, CS)已是当前信号处理领域中的一个重要理论,相关的信号重构算法更是备受国内外众多学者的关注。相比于传统的信号采样,具有采样频率低、耗时少、压缩占有空间小等一系列优势[1−3]。压缩感知理论中有3个重点问题,分别为学习字典设计、观测矩阵构造和信号重构算法[4],每一个问题都对信号重构起着重要的作用。
本文利用压缩感知模型和欠定盲源分离模型的等效性,研究了压缩感知在欠定盲源分离中的源信号重构问题,并针对学习字典设计与重构算法的某些缺陷进行改进。首先,提出相关性加权最小二乘字典学习方法,与K−SVD字典学习方法相比,具有超线性收敛速度,提高了字典的学习效率,并有助于信号重构质量的提高[5]。然后,利用分段正交匹配追踪算法来重构源信号。接着,将字典学习法与信号重构算法结合,可在算法复杂度与重构精度上,实现更好的折中。最后通过实验仿真分析证明,压缩感知可以较高的精度实现源信号的精确分离。
1 压缩感知问题描述 1.1 盲源分离与压缩感知等效模型在无噪声条件下,盲源分离混合系统的数学表达式为:
| $ {X}(t) = {AS}(t) $ | (1) |
将式(1)转换成式(2)的矩阵相乘形式:
| $ \left[ {\begin{array}{*{20}{c}} {{x_1}(t)}\\ {{x_2}(t)}\\ \vdots \\ {{x_M}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1N}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2N}}}\\ \vdots & \cdots & \cdots & \vdots \\ {{a_{M1}}}&{{a_{M2}}}& \cdots &{{a_{MN}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{s_1}(t)}\\ {{s_2}(t)}\\ \vdots \\ {{s_N}(t)} \end{array}} \right] $ | (2) |
假设系统中的信号均为离散实值信号,且采样点数均为
压缩感知系统模型的数学表达式为:
| $ {X} = {\varPhi S} $ | (3) |
同样转换成式(4)的矩阵相乘形式:
| $ \left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ \vdots \\ {{x_M}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\varphi _{11}}}&{{\varphi _{12}}}& \cdots &{{\varphi _{1N}}} \\ {{\varphi _{21}}}&{{\varphi _{22}}}& \cdots &{{\varphi _{2N}}} \\ \vdots & \cdots & \cdots & \vdots \\ {{\varphi _{M1}}}&{{\varphi _{M2}}}& \cdots &{{\varphi _{MN}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{s_1}} \\ {{s_1}} \\ \vdots \\ {{s_N}} \end{array}} \right] $ | (4) |
式中:
| $ {S} = \sum\limits_{i = 1}^N {{b_i}{{\psi }_i}} $ | (5) |
综合上面的表达形式,压缩感知系统模型的数学表达式改写为式(6)的形式:
| $ {\varGamma } = {\varPhi \varPsi } $ | (6) |
令
对比这2种模型,可以发现表达形式很相近。为了结合这2种模型,将式(2)中的
| $ {X} = {\left[ {{x_1}\left( 1 \right), \cdots ,{x_1}\left( T \right), \cdots ,{x_M}\left( 1 \right), \cdots ,{x_M}\left( T \right)} \right]^{\rm{T}}} $ | (7) |
| $ {S} = {\left[ {{s_1}\left( 1 \right), \cdots ,{s_1}\left( T \right), \cdots ,{s_N}\left( 1 \right), \cdots ,{s_N}\left( T \right)} \right]^{\rm{T}}} $ | (8) |
套用观测矩阵的格式,将混合矩阵
| $ {{\varphi }_{ij}} = \left[ {\begin{array}{*{20}{c}} {{a_{ij}}}&0& \cdots &0 \\ 0&{{a_{ij}}}& \cdots &0 \\ \vdots & \cdots & \cdots & \vdots \\ 0&0& \cdots &{{a_{ij}}} \end{array}} \right] $ | (9) |
此时
利用压缩感知理论完成源信号重构的基本内容有3个:字典学习方法、观测矩阵构造、信号重构算法。
1.2.1 字典学习将源信号作为学习信号,根据源信号的先验知识并运用学习方法,得到稀疏字典,常见的有最优方向法、K−奇异值分解(K−SVD)算法等[7]。本文采用一种改进的加权最小二乘算法,进行字典学习,该算法可根据信号内部信息,提高信号重构精度。
1.2.2 观测矩阵构造将欠定盲源分离的数学模型转换成压缩感知的数学模型,将混合矩阵转化为压缩感知中的测量矩阵。可按照1.1节内容实现。
1.2.3 重构算法压缩感知重构算法有很多,一类算法为凸优化算法,例如基追踪(base pursuit, BP)算法等;另一类算法为贪婪追踪算法,例如正交匹配追踪(orthogonal matching pursuit, OMP)算法、互补匹配追踪(complementary matching pursuit, CMP)算法等[8]。本文重点研究贪婪追踪算法中OMP算法的改进算法,求出信号的稀疏系数。最后实现源信号的重构,解决欠定盲源信号的分离问题。
2 压缩感知盲源分离算法 2.1 CWLS-DL方法本文采用一种名为含相关性的加权最小二乘字典学习(correlation-based weighted least square– dictionary learning, CWLS−DL)方法,它是一种能充分挖掘信号内部相关性特征的字典学习方法,能够提高过完备字典在压缩感知中的信号重构精度。
首先,给出原始的训练样本,如式(10)所示。
| $ {S}\left( t \right) = \left[ {{s_i}\left( t \right)} \right]_{i = 1}^N $ | (10) |
训练字典为
| $ {B}\left( t \right) = \left[ {{{b}_i}\left( t \right)} \right]_{i = 1}^N $ | (11) |
式中:
然后,进行字典学习阶段,分为稀疏编码和字典更新2个环节[10]。稀疏编码,先将子训练字典固定,基于选定的匹配追踪(matching pursuit, MP)算法,求出子稀疏系数向量。字典更新,固定已求出的子稀疏系数向量,使用加权最小二乘法算法更新子训练字典。
下面给出利用加权最小二乘法,得到训练字典更新公式的简要推导过程。在字典更新中,要解决带权重的重构信号与输入信号误差的F−范数最小化问题,也就是式(12)与(13)所表示的关系:
| $ \arg \mathop {\min }\limits_{{{d}_i}} f\left( {{{d}_i}} \right) = \arg \mathop {\min }\limits_{{{d}_i}} \left\{ {{{\left\| {\left( {{S} - \sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} } \right){{W}_0}} \right\|}_F}^2} \right\} $ | (12) |
| $ {\rm{s}}{\rm{.t}}.\forall i,{\left\| {{b_i}} \right\|_0} = {K_0} $ | (13) |
式中:
| $ \begin{array}{l} {\left\| {\left( {{S} - \displaystyle\sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} } \right){{W}_0}} \right\|_F}^2 = {\rm{tr}}\left( {{SW}{{S}^{\rm{T}}}} \right) - {\rm{tr}}\left( {{SW}{{\left( {\displaystyle\sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} } \right)}^{\rm{T}}}} \right) - \\ {\rm{tr}}\left( {{{\left( {\displaystyle\sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} } \right)}^{\rm{T}}}{W}{{S}^{\rm{T}}}} \right) + {\rm{tr}}\left( {{{\left( {\displaystyle\sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} } \right)}^{\rm{T}}}{W}{{\left( {\displaystyle\sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} } \right)}^{\rm{T}}}} \right) \end{array} $ | (14) |
式中:
对函数
| $ \sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} = {SW}{\left( {\sum\limits_{i = 1}^N {{{b}_i}} } \right)^{\rm{T}}}{\left[ {{W}{{\left( {\sum\limits_{i = 1}^N {{{b}_i}} } \right)}^{\rm{T}}}} \right]^{ - 1}} $ | (15) |
式(15)表示为N组方程组,将式(15)的结果带入式(16),计算误差矩阵
| $ {R} = {S} - \sum\limits_{i = 1}^N {{{d}_i}{{b}_i}} = \left[ {{r}\left( 1 \right),{r}\left( 2 \right), \cdots ,{r}\left( T \right)} \right] $ | (16) |
根据得到的误差矩阵
| $ {W}^{'} = {\rm{diag}}\left[ {\frac{1}{{{{\left\| {{r}\left( 1 \right)} \right\|}_2}^2}},\frac{1}{{{{\left\| {{r}\left( 2 \right)} \right\|}_2}^2}}, \cdots ,\frac{1}{{{{\left\| {{r}\left( T \right)} \right\|}_2}^2}}} \right] $ | (17) |
式中
所以,
得到权重矩阵
| $ {\varPsi } = \left[ {{{\psi }_1},{{\psi }_2}, \cdots ,{{\psi }_N}} \right] $ | (18) |
分段正交匹配追踪(Stage wise-OMP, St-OMP)算法是OMP的一种改进算法,也是压缩感知理论中的核心[11]。St-OMP算法在OMP算法基础上,增加了单次迭代选择的原子数,并且不受到信号稀疏度的影响,相比于OMP算法和其他改进的OMP算法,有独特优势。
2.2.1 算法涉及到的变量与成分输入成分:
1)感知矩阵:
2)观测信号:
3)迭代次数:
4)阈值:
输出成分:
1)稀疏系数向量估计值:
2)残差:
其他变量:
1)迭代次数:
2)每次迭代找到的索引(列序号):
3)t次迭代索引(列序号)集合:Λt。
4)
5)按Λt选出的矩阵Γ的列集合:Γt。
6)门限值
1)将参数初始化:
2)计算
| $ u = {\rm{abs}}\left[ {{{\varGamma }_t}^{\rm{T}}{{r}_{t - 1}}} \right] = \left| {\left\langle {{{r}_{t - 1}},{{\gamma }_j}} \right\rangle } \right| $ | (19) |
3)按式(20)进行集合并运算,若Λt=Λt-1(即没有新列被选中),则停止迭代,进入步骤7);
| $ {{\varLambda }_t} = {{\varLambda }_{t - 1}} {{\text{∪}}} \left\{ {{J_0}} \right\}{\rm{,}}{{\varGamma }_t} = {{\varGamma }_{t - 1}} {{\text{∪}}} \left\{ {{{\gamma }_j}} \right\} $ | (20) |
4)求
| $ {\hat{ B}_t} = \arg \mathop {\min }\limits_{{{B}_t}} \left\| {{X} - {{\varGamma }_t}{{B}_t}} \right\| = {\left( {{{\varGamma }_t}^{\rm{T}}{{\varGamma }_t}} \right)^{ - 1}}{{\varGamma }_t}^{\rm{T}}{X} $ |
5)按式(21)进行残差更新计算;
| $ {{r}_t} = {X} - {{\varGamma }_t}{\hat{ B}_t} = \left\{ {{I} - {{\varGamma }_t}\left[ {{{\left( {{{\varGamma }_t}^{\rm{T}}{{\varGamma }_t}} \right)}^{ - 1}}{{\varGamma }_t}^{\rm{T}}} \right]} \right\}{X} $ | (21) |
6)迭代次数增加,即
7)得到最终的
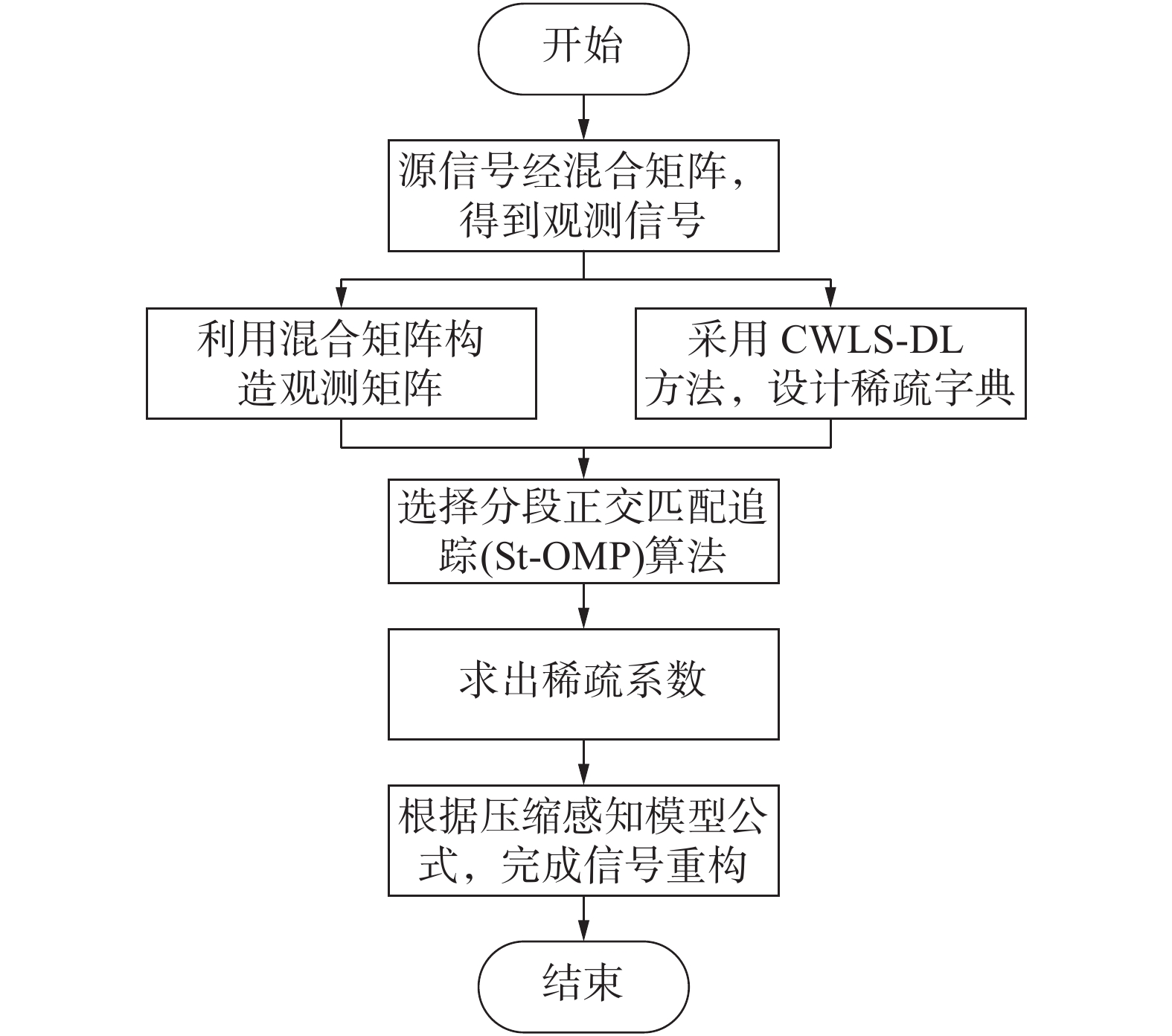
组合算法流程图如图1所示。
|
Download:
|
| 图 1 压缩感知盲源分离组合算法 | |
评价混合矩阵估计性能的标准有2个[12],分别为:
1)信干比
| ${R_{{\rm{SIR}}}} = 10\lg {\left( {\frac{{{{\left\| {{s_i}} \right\|}_2}}}{{{{\left\| {{{\hat s}_i} - {s_i}} \right\|}_2}}}} \right)^2}$ |
式中:
2)相关系数
| ${\varepsilon _i} = {\rm{cor}}\left( {{{\hat s}_i}(t),{s_i}(t)} \right) = \displaystyle\frac{{\left| {\displaystyle\sum\limits_{i = 1}^N {{{\hat s}_i}(t){s_i}(t)} } \right|}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^N {{{\hat s}_i}^2(t)\displaystyle\sum\limits_{i = 1}^N {{s_i}^2(t)} } } }}$ |
式中:
为验证算法的性能,我们通过语音信号的盲源分离仿真实验来完成。实验采用的源信号为随机选取的4段英语听力音频,数据采样点长度为80 000,采样频率为10 kHz,源信号时域波形图如图2所示。

|
Download:
|
| 图 2 源信号波形 | |
首先,利用混合矩阵模拟声音传播的信道,将4路源信号混合成3路观测信号,本文中混合矩阵
| ${A} = \left[ {\begin{array}{*{20}{c}} {0.750 \; 3}&{ - 0.858 \; 7}&{0.661 \; 9}&{ - 0.262 \; 6} \\ {0.532 \; 7}&{0.175 \; 3}&{0.985 \; 6}&{0.334 \; 3} \\ { - 0.068 \; 7}&{0.464 \; 2}&{0.367 \; 0}&{0.730 \; 9} \end{array}} \right]$ |
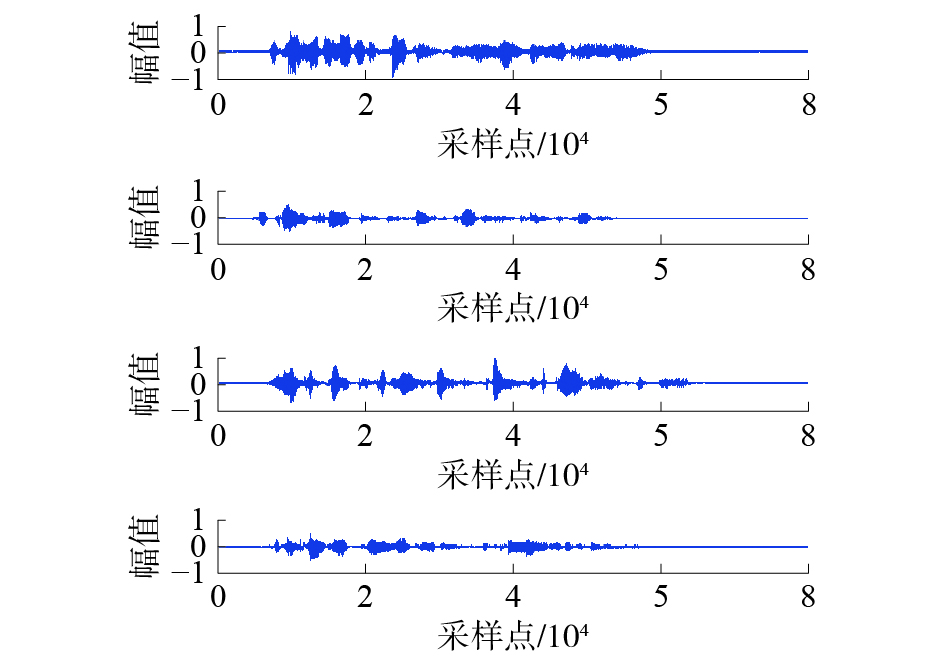
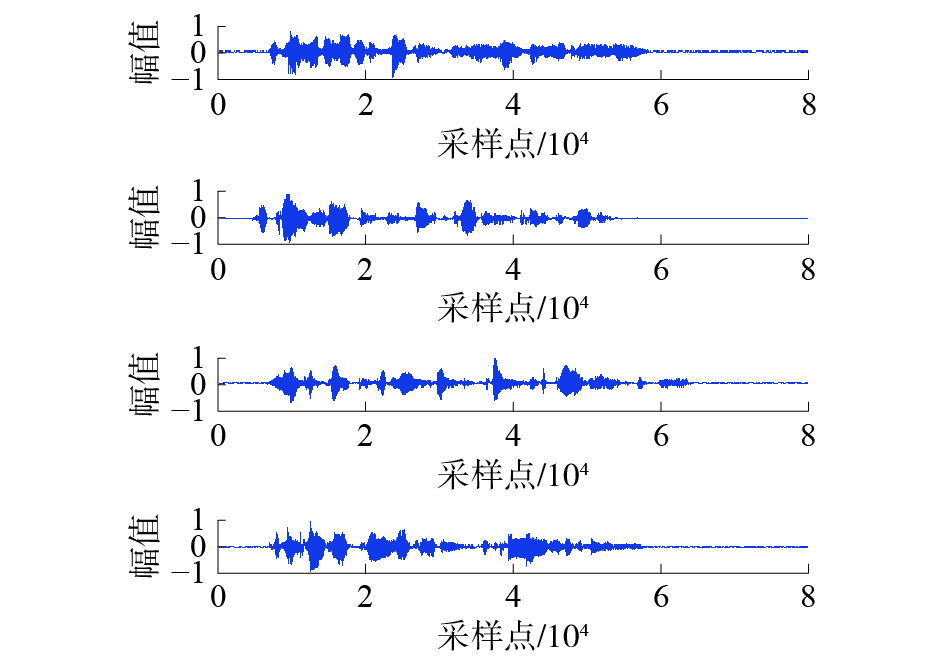
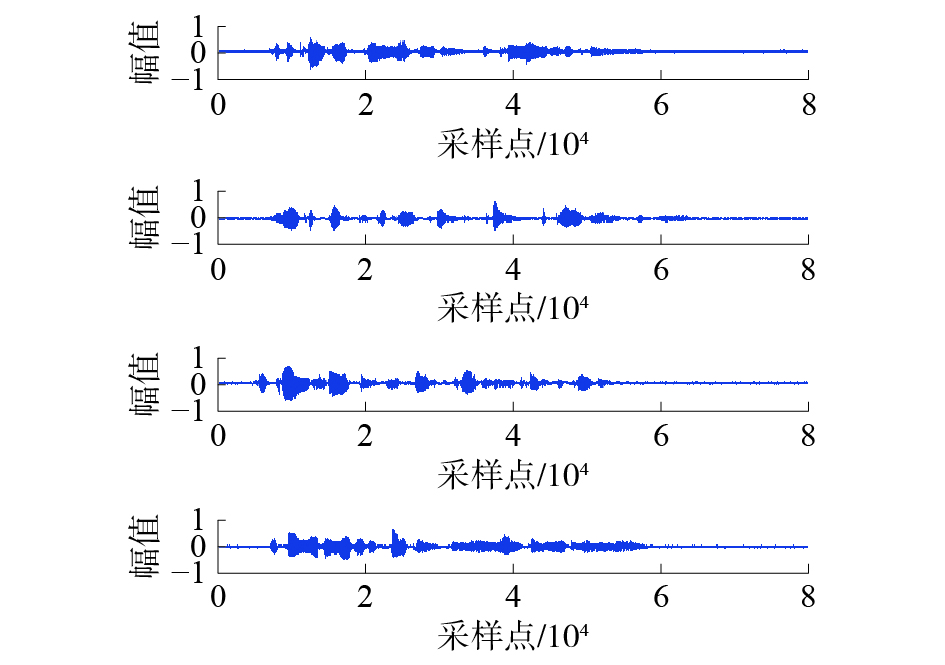
根据本文提出的字典学习方法与重构算法,进行信号分离重构仿真实验,并命名算法1为K−SVD字典+OMP算法,算法2为CWLS字典+OMP算法,算法3为K−SVD字典+St−OMP算法,算法4为CW−LS字典+St−OMP算法。分别通过上述组合算法进行源信号重构,得到重构源信号分别如图3~6所示。
|
Download:
|
| 图 3 算法1分离信号波形(无噪声) | |
|
Download:
|
| 图 4 算法2分离信号波形(无噪声) | |
|
Download:
|
| 图 5 算法3分离信号波形(无噪声) | |
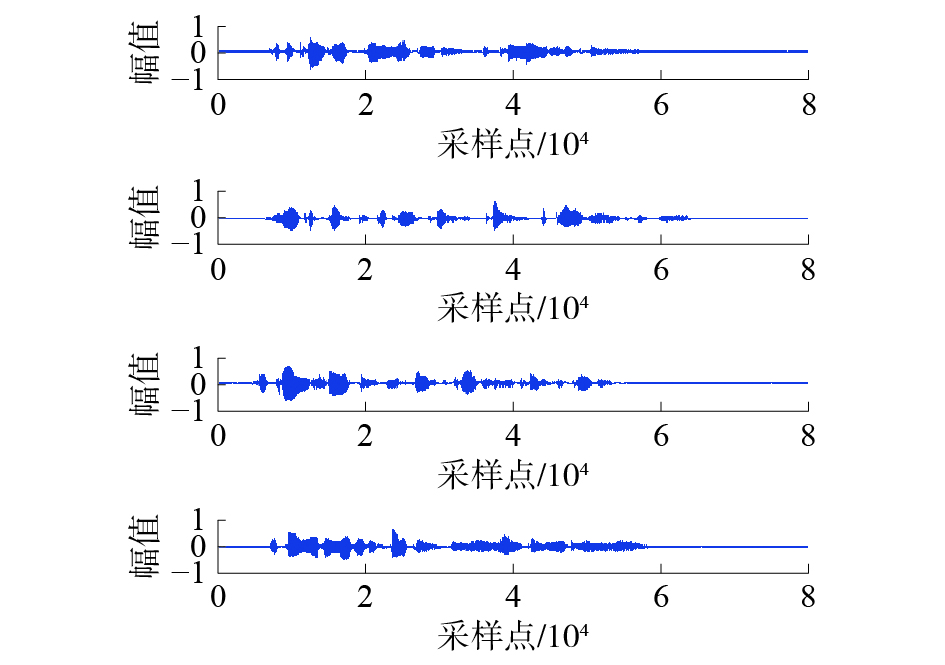
|
Download:
|
| 图 6 算法4分离信号波形(无噪声) | |
接下来,通过对比所得相关系数与信干比的数据,来检验算法的性能。
首先是相关系数,表1中的数据为通过算法4重构信号得到的相关系数,主对角线上的数据代表源信号与自身重构信号的相关系数,其他位置代表源信号与其余重构信号的相关系数。可以看到主对角线上的相关系数均大于0.8,证明通过算法4能够较好恢复信号。
|
|
表 1 通过算法4仿真得到的相关系数 |
下面将对比通过不同算法得到的相关系数来验证算法重构源信号的精确度,数据如表2所示。其中,在算法4下计算得到的相关系数最大,意味着重构源信号的精确度最高。所以,CWLS字典与St−OMP算法的组合在信号重构精度方面,在这4个算法组合中性能最佳。
|
|
表 2 不同算法相关系数对比结果 |
下面将对比不同算法完成仿真实验的消耗时间,来验证算法重构源信号的复杂度。数据如表3所示,按算法消耗时间由少到多的顺序排列,分别为算法2、算法1、算法4、算法3。这证明了CWLS字典与St-OMP算法的组合,在算法复杂度上有一个降低的趋势。
|
|
表 3 不同算法消耗时间对比结果 |
对比相关系数之后,下面是信干比的比较。数据如表4所示,其中算法4得到的信干比最大。和相关系数的验证结果一样,CWLS字典与St-OMP算法的组合在信号重构精度方面,是这4个算法组合中性能最好的。
|
|
表 4 不同算法信干比对比结果 |
本小节实验将在加性高斯白噪声(additive white Gaussian noise, AWGN)的环境下进行。依旧遵循3.1.1节中的算法命名方式,分别通过前面的4种组合算法进行源信号重构。设置信噪比为20 dB,得到重构源信号分别如图7~10所示。

|
Download:
|
| 图 7 算法1分离信号波形(信噪比为20 dB) | |
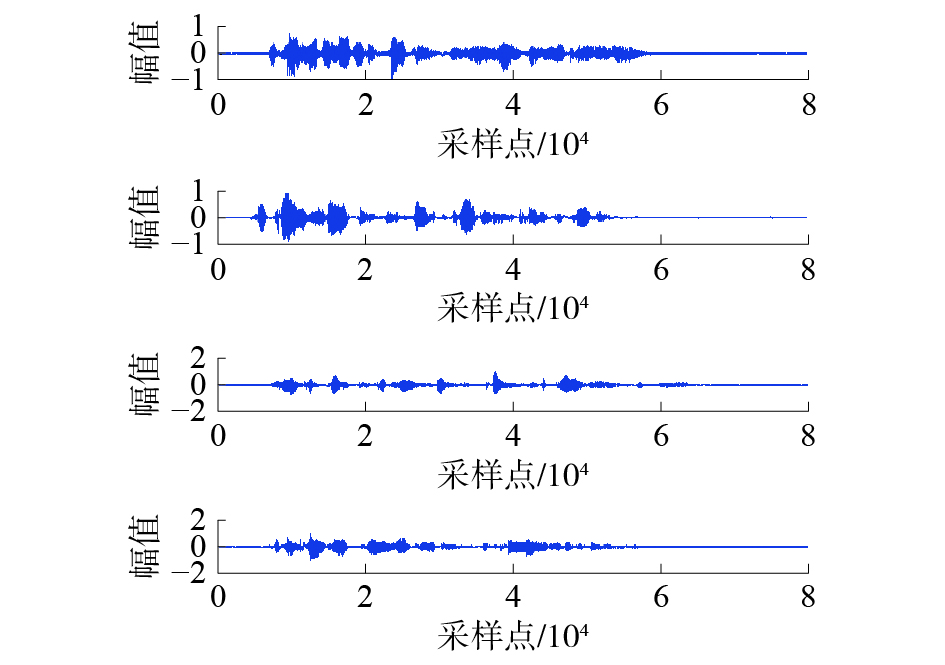
|
Download:
|
| 图 8 算法2分离信号波形(信噪比为20 dB) | |

|
Download:
|
| 图 9 算法3分离信号波形(信噪比为20 dB) | |
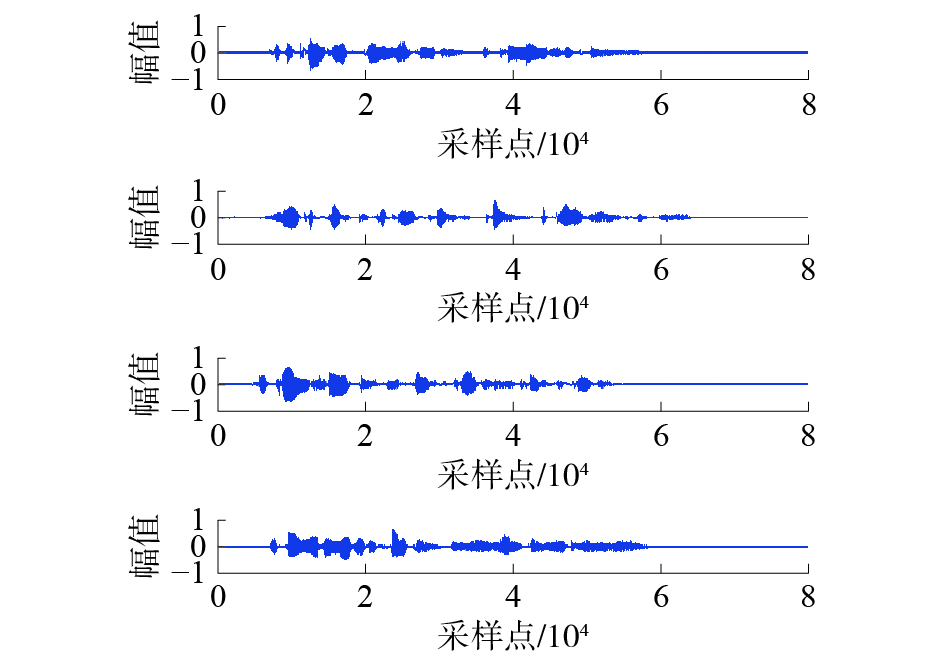
|
Download:
|
| 图 10 算法4分离信号波形(信噪比为20 dB) | |
这里对比在AWGN环境下所得相关系数与信干比的数据,来检验算法的性能。
图11为不同信噪比下的相关系数曲线图,可看到算法4是上述4种组合中,当相关系数相等且不小于0.8时,所需信噪比最小的组合,最小信噪比约为18 dB。
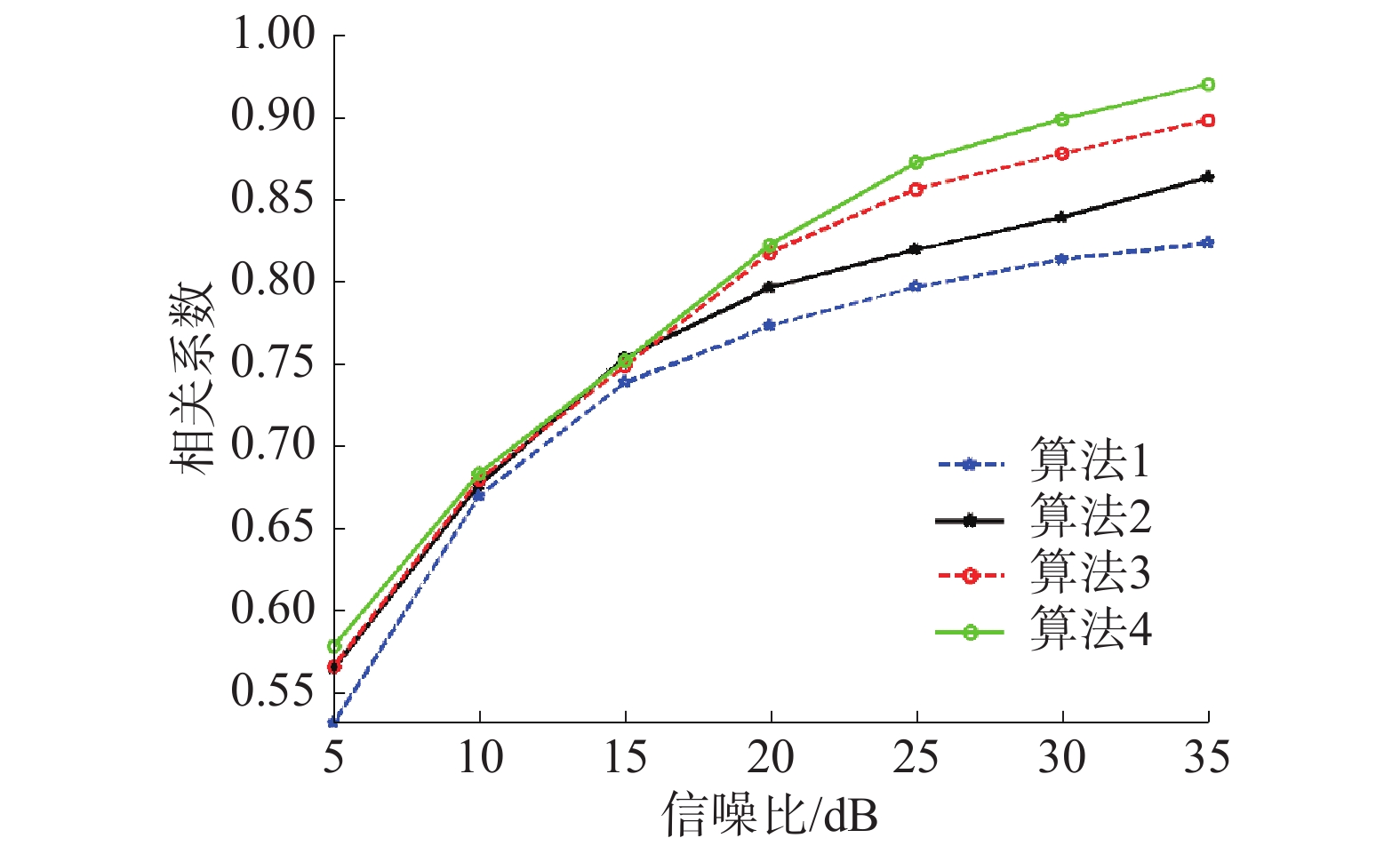
|
Download:
|
| 图 11 不同信噪比下的相关系数(含AWGN)曲线 | |
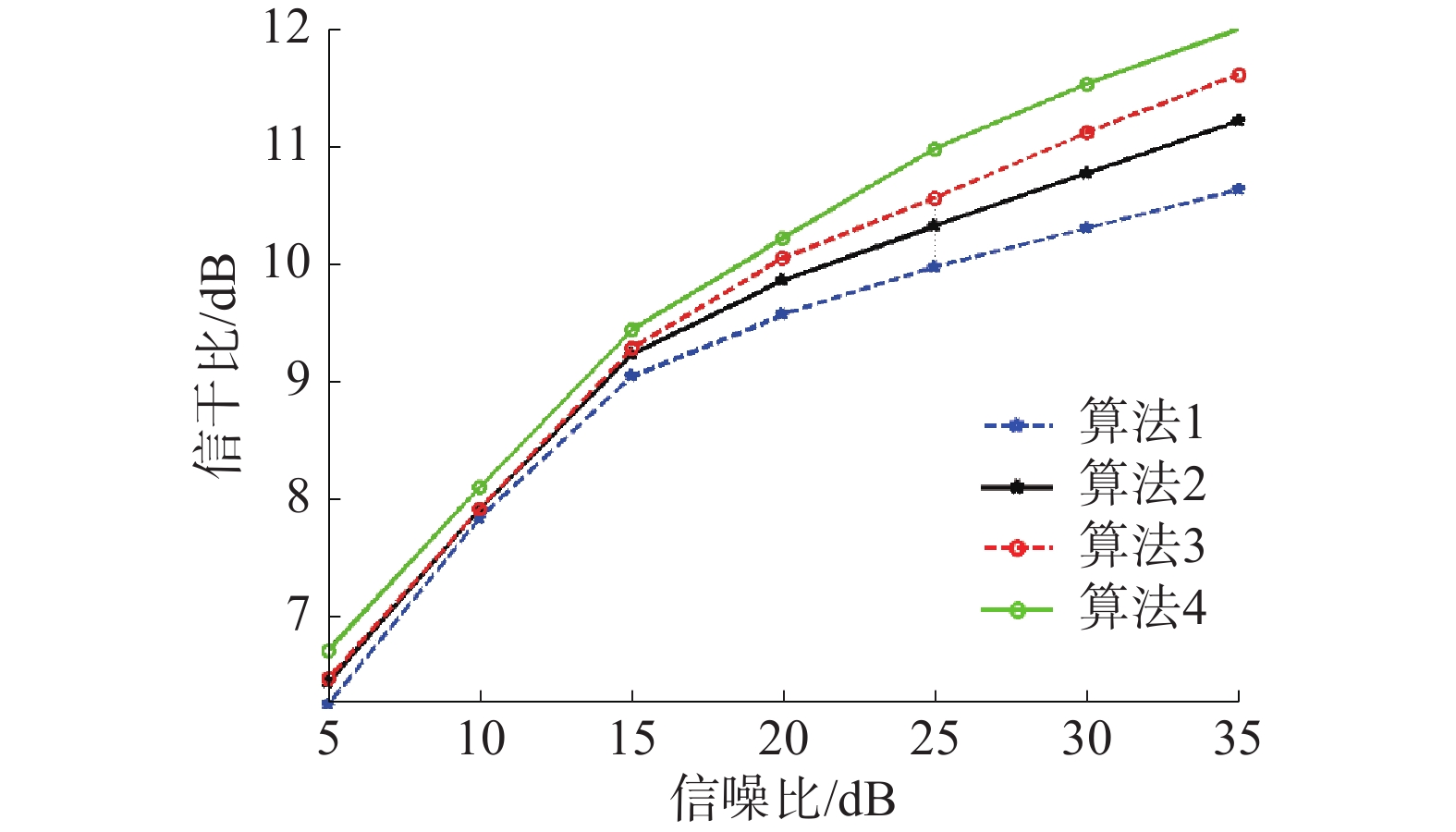
图12为不同信噪比下的信干比曲线图,可看出算法4的组合是上述4种组合中,当信干比相等且不小于10 dB时,所需信噪比最小的组合,最小信噪比约为17 dB。
|
Download:
|
| 图 12 不同信噪比下的信干比(含AWGN)曲线 | |
所以,CWLS字典与St-OMP算法的组合在含噪声环境下同样有着较优的性能。
4 结论本文就欠定盲源分离中源信号的恢复问题,与压缩感知理论结合,并针对其中的字典学习与重构算法进行改进,提出了CWLS字典学习与St-OMP算法组合,并完成语音信号的信号重构仿真实验。所得结论如下:
1)提出的组合算法能够解决带权重信号误差的F−范数最小化问题,并通过增加单次迭代的原子数改变算法复杂度。
2)仿真实验结果表明,CWLS字典学习与St-OMP算法组合在原有算法基础上,可提高信号重构精度,同时在算法复杂度上有着不错的折中效果;而且在含噪声环境下同样有着较优的性能。
文章在对算法的复杂度验证上还不够完善,而且其稳定性也要进一步验证,这也是后面的研究过程中需要考虑的地方。
| [1] |
许华杰, 何敬禄, 胡小明. 基于块稀疏度估计的压缩感知自适应重构算法[J]. 计算机应用研究, 2018, 35(1): 305-308, 320. DOI:10.3969/j.issn.1001-3695.2018.01.065 ( 0) 0)
|
| [2] |
BARNICH O, VAN DROOGENBROECK M. ViBe: a universal background subtraction algorithm for video sequences[J]. IEEE transactions on image processing, 2011, 20(6): 1709-1724. DOI:10.1109/TIP.2010.2101613 ( 0) 0)
|
| [3] |
ELAD M. Optimized projections for compressed sensing[J]. IEEE transactions on signal processing, 2007, 55(12): 5695-5702. DOI:10.1109/TSP.2007.900760 ( 0) 0)
|
| [4] |
何继爱, 刘向阳. 压缩感知理论及其在盲源分离中的应用[J]. 测控技术, 2016, 35(11): 149-152. DOI:10.3969/j.issn.1000-8829.2016.11.037 ( 0) 0)
|
| [5] |
王粒宾, 崔琛, 李莹军. 基于加权最小二乘的字典学习算法[J]. 系统工程与电子技术, 2011, 33(8): 1896-1900. DOI:10.3969/j.issn.1001-506X.2011.08.41 ( 0) 0)
|
| [6] |
张红丽. 基于稀疏性增强的欠定盲源分离算法研究[D]. 秦皇岛: 燕山大学, 2016: 30.
( 0) 0)
|
| [7] |
徐健, 常志国, 张小丹. 采用交替K-奇异值分解字典训练的图像超分辨率算法[J]. 武汉大学学报(信息科学版), 2017, 42(8): 1137-1143. ( 0) 0)
|
| [8] |
FU Weihong, CHEN Jiehu, YANG Bo. Source recovery of underdetermined blind source separation based on SCMP algorithm[J]. IET signal processing, 2017, 11(7): 877-883. DOI:10.1049/iet-spr.2015.0100 ( 0) 0)
|
| [9] |
叶娅兰, 何文文, 程云飞, 等. 面向压缩感知的基于相关性字典学习算法[J]. 电子科技大学学报, 2017, 46(5): 703-708. DOI:10.3969/j.issn.1001-0548.2017.05.011 ( 0) 0)
|
| [10] |
练秋生, 王小娜, 石保顺, 等. 基于多重解析字典学习和观测矩阵优化的压缩感知[J]. 计算机学报, 2015, 38(6): 1162-1171. ( 0) 0)
|
| [11] |
汪浩然, 夏克文, 牛文佳. 分段正交匹配追踪(StOMP)算法改进研究[J]. 计算机工程与应用, 2017, 53(16): 55-61. DOI:10.3778/j.issn.1002-8331.1604-0226 ( 0) 0)
|
| [12] |
CHEN P, PENG D H, ZHEN L L, et al. Underdetermined blind separation by combining Sparsity and independence of sources[J]. IEEE access, 2017, 5: 21731-21742. DOI:10.1109/ACCESS.2017.2764044 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


