分布式光纤传感系统已经成为大型土木工程，如桥隧、地下管道、铁路、大坝等结构健康情况监测不可或缺的技术^[1]，其中BOTDA型分布式光纤传感器由于在温度和应变检测中具有高精度、长传感距离、高空间分辨率和强信号等优势受到越来越多的关注^[2]。布里渊散射谱频移变化量与温度、应变的变化量之间存在一种线性关系^[3]，通过对布里渊散射谱频移变化量的检测即可得到温度和应变的变化情况。因此，高精度提取布里渊散射谱特征对BOTDA型分布式光纤传感技术性能提升具有重要意义。

目前，很多学者提出了不同的布里渊散射谱拟合算法。2014年，赵丽娟等^[4]提出三参数最小二乘拟合的Levenberg−Marquart（LM）优化算法估计布里渊散射参数，并使用粒子群优化算法产生初值。2015年，Li等^[5]提出多项式拟合方法寻找不完整的洛伦兹线型布里渊散射谱峰值。2016年，张燕君等^[6]提出基于自适应惯性权重和混沌优化的粒子群优化算法提取布里渊散射谱特征，并与有限元LM算法、粒子群LM算法和粒子群优化算法进行了比较。2017年，Chung等^[7]应用交叉递归图分析方法提取分布式光纤传感中因温度和应变变化引起的布里渊频移。然而，目前提出的一些方法仍存在依赖初值，易陷入局部极值的不足。随着对土木结构健康监测精度、实时性和智能化要求的不断提高，一些基于智能优化算法的人工神经网络方法被提出来^[8]。本文提出差分进化算法优化广义回归神经网络（DE−GRNN）拟合布里渊散射谱，并对不同信噪比（ ${R_{{\rm{SN}}}}$ ）、不同线宽下Pseudo−Voigt型布里渊散射谱进行拟合。仿真结果分析表明，DE算法可以实现对GRNN光滑因子自动寻优，DE−GRNN算法有较强的非线性曲线逼近能力，混合优化算法可以实现高精度拟合布里渊散射谱。

1 基本原理 1.1 布里渊散射谱模型

在BOTDA型分布式光纤传感系统中，泵浦光和探测光分别从光纤两端注入，两束光相遇时由于电致伸缩效应发生受激布里渊散射，产生后向传输的布里渊散射光，这一能量转换过程可以用三波耦合方程描述^[9]，光纤中理想布里渊散射增益谱呈洛伦兹线型^[10]：

${g_B}\left( v \right) = {g_0}\frac{{{{\left( {\Delta {v_B}/2} \right)}^2}}}{{{{\left( {v - {v_B}} \right)}^2} + {{\left( {\Delta {v_B}/2} \right)}^2}}}$

式中： $v$ 为布里渊频率； ${v_B}$ 为布里渊中心频移； $\Delta {v_B}$ 为布里渊散射谱增益最大值的半高全宽； ${g_0}$ 为布里渊增益谱最大值。

然而在实际测量中由于一些干扰因素，布里渊散射谱会逐渐展宽，由洛伦兹线型趋向高斯线型，布里渊散射谱以某比例介于2种线型之间，可以描述为Pseudo-Voigt型拟合函数^[11]：

$ \begin{array}{l} {f_B}\left( v \right) = k\displaystyle\frac{{{{\left( {\Delta {v_{{B_1}}}/2} \right)}^2}}}{{{{\left( {v - {v_B}} \right)}^2} + {{\left( {\Delta {v_{{B_1}}}/2} \right)}^2}}} + \\ \qquad\quad \left( {1 - k} \right)\exp [ - 2.773{\left( {\Delta {v_{{B_2}}}^{ - 2}\left( {v - {v_B}} \right)} \right)^2}] \\ \end{array} $

(1)

式中： $k$ 为权重比； ${v_B}$ 布里渊中心频移； $\Delta {v_{{B_1}}}$ 为洛伦兹谱型线宽； $\Delta {v_{{B_2}}}$ 为高斯谱型线宽。

1.2 广义回归神经网络

广义回归神经网络是Specht^[12]博士于1991年提出的，其基于Parzen Window在1962年提出的估计器理论。广义回归神经网络是径向基（radial basis function，RBF）神经网络的一种，由于其出色的非线性拟合性能，经常用于函数逼近^[13]。相比于RBF网络，GRNN训练方式更简便并且只有一个需要确定的参数，Specht博士在其论文中证明，GRNN只需要后向传输神经网络训练样本量的1%，就可以获得与其相同的预测效果^[14]。

在GRNN中，假设变量 $y$ 可以表示为独立变量 $x$ 的函数，即 $y = f\left( x \right)$ 。 $y$ 对 $x$ 的条件均值为式（2），Parzen非线性估计密度函数 $g\left( {x,y} \right)$ 定义为式（3）：

$E[y|x] =\frac{{ \displaystyle\int_{ - \infty }^\infty {yg(x,y){\rm{d}}y} }}{{ \displaystyle\int_{ - \infty }^\infty {g(x,y){\rm{d}}y} }}$

(2)

$\begin{array}{l} g(x,y) = \displaystyle\frac{1}{{{{(2{\rm{{\text{π}} }})}^{\frac{{(m + 1)}}{2}}}{\sigma ^{(m + 1)}}}} \cdot \displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {\exp \left[ - \displaystyle\frac{{{{({{x}} - {x_i})}^{\rm{T}}}({{x}} - {x_i})}}{{2{\sigma ^2}}}\right]} \cdot \\ \qquad \qquad \exp \left[ - \displaystyle\frac{{{{({{y}} - {y_i})}^2}}}{{2{\sigma ^2}}}\right] \end{array} $

(3)

式中： ${x_i}$ 、 ${y_i}$ 分别为随机变量 $x$ 、 $y$ 的样本值； $m$ 是向量 ${{x}}$ 的维数； $n$ 为训练样本数； $\sigma $ 为高斯函数的宽度系数，称为扩展常数或光滑因子^[15]。

扩展常数是GRNN中唯一需要确定的参数，因此扩展常数的选择直接影响曲线拟合精度。当扩展常数取值过大时，估计值趋近于所有独立变量的均值，曲线很光滑但不能准确代表训练样本。当扩展常数趋近于零时，拟合值会非常接近样本中相应的独立变量，但是拟合曲线不光滑，并且一旦某点没有包含在样本里，拟合性能会大大降低，这种现象称为过拟合。因此，在实际应用中需要根据要求的精度和光滑度合理选择扩展常数。将式（3）代入式（2），改变积分求和的顺序，可得到理想估计值 $\hat y$ 为：

$\hat y(x) = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {{y_i}\exp \left( { - \displaystyle\frac{{{{({{x}} - {x_i})}^{\rm{T}}}({{x}} - {x_i})}}{{2{\sigma ^2}}}} \right)} }}{{\displaystyle\sum\limits_{i = 1}^n {\exp \left( - \displaystyle\frac{{{{({{x}} - {x_i})}^{\rm{T}}}({{x}} - {x_i})}}{{2{\sigma ^2}}}\right)} }}$

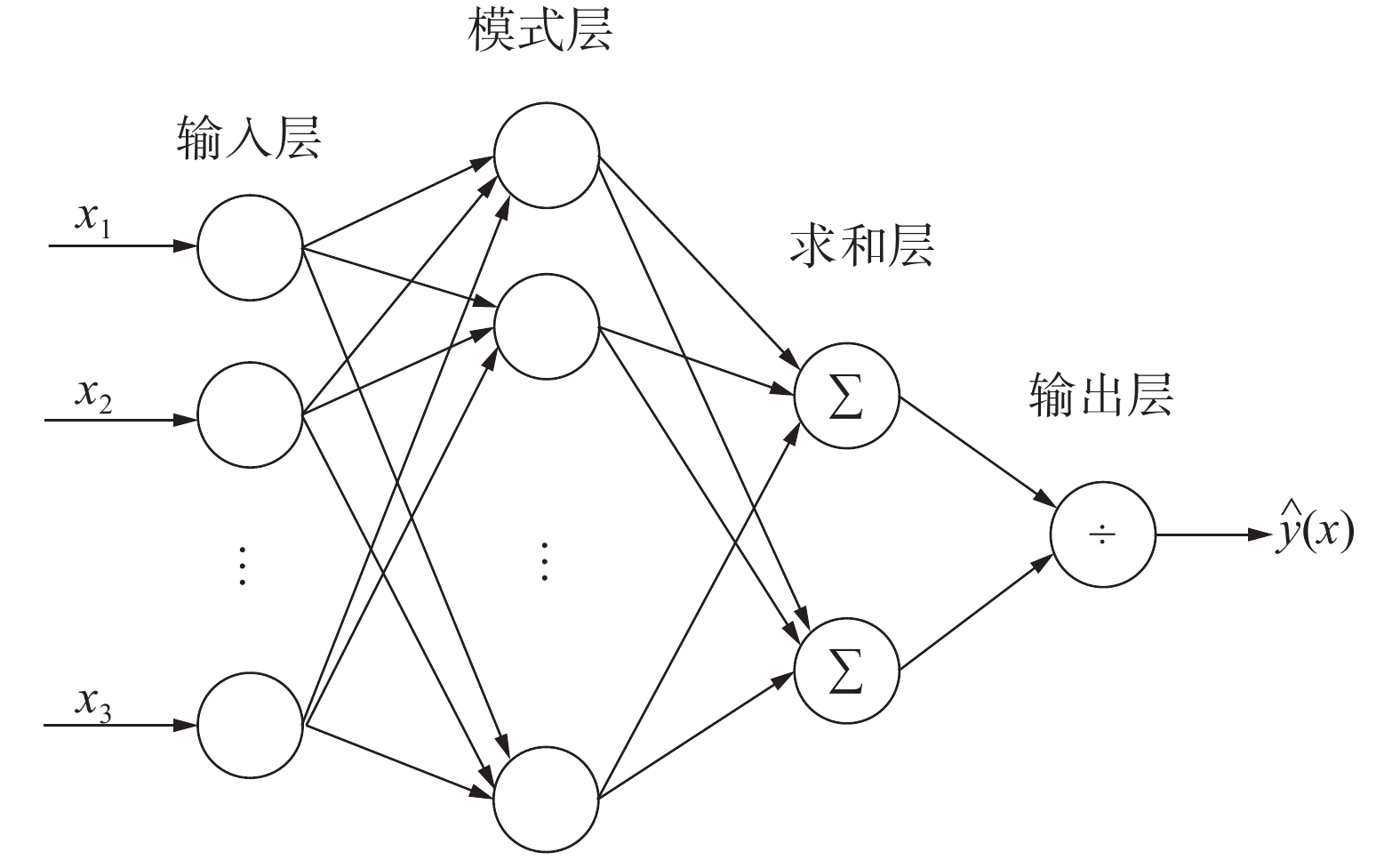
GRNN结构模型相似于RBF网络结构，由4层组成，分别是输入层、模式层、求和层、输出层，如图1所示。输入层的元素是简单的线性神经元，每个神经元对应输入的参数 $x$ ；模式层也叫隐含回归层，每个神经元对应一个训练样本；求和层有2个神经元，一个计算模式层的线性权重和，另一个计算模式层实际目标值的权重和，估计值 $\hat y$ 等于2部分和之商。

1.3 DE-GRNN混合优化算法

差分进化算法是一种利用种群中个体之间合作和竞争而产生的智能优化搜索算法^[16]。待优化问题的解被视为搜索范围内一个种群，通过变异、交叉、选择等操作，目标函数趋近于预先设定的最优值，解的精度不断提高。DE具有较强的全局收敛能力和鲁棒性，采取实数进行编码、基于差分的简单变异操作和“一对一”的竞争策略，减少进化计算操作复杂性，其特有的记忆能力可以动态追踪当前搜索状况，并调整搜索策略，适用于求解较为复杂的优化问题^[17]。

DE−GRNN算法中，利用DE搜索GRNN的最优扩展常数。DE随机产生初始扩展常数种群，进行迭代寻优直至达到最大迭代次数，将获得的最优扩展常数代入GRNN中进行曲线拟合。拟合值和真实值之间欧几里得距离的倒数用于评价差分进化操作得到的最优个体的性能，即适应度函数。当欧几里得距离越来越小，则拟合值越来越大，意味着拟合曲线趋近于真实值，有更好的拟合精度，适应度函数为：

$f(m) =\displaystyle \frac{1}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({m_i} - {M_i})}^2}} } }}$

式中： ${m_i}$ 为拟合值； ${M_i}$ 为真实值。

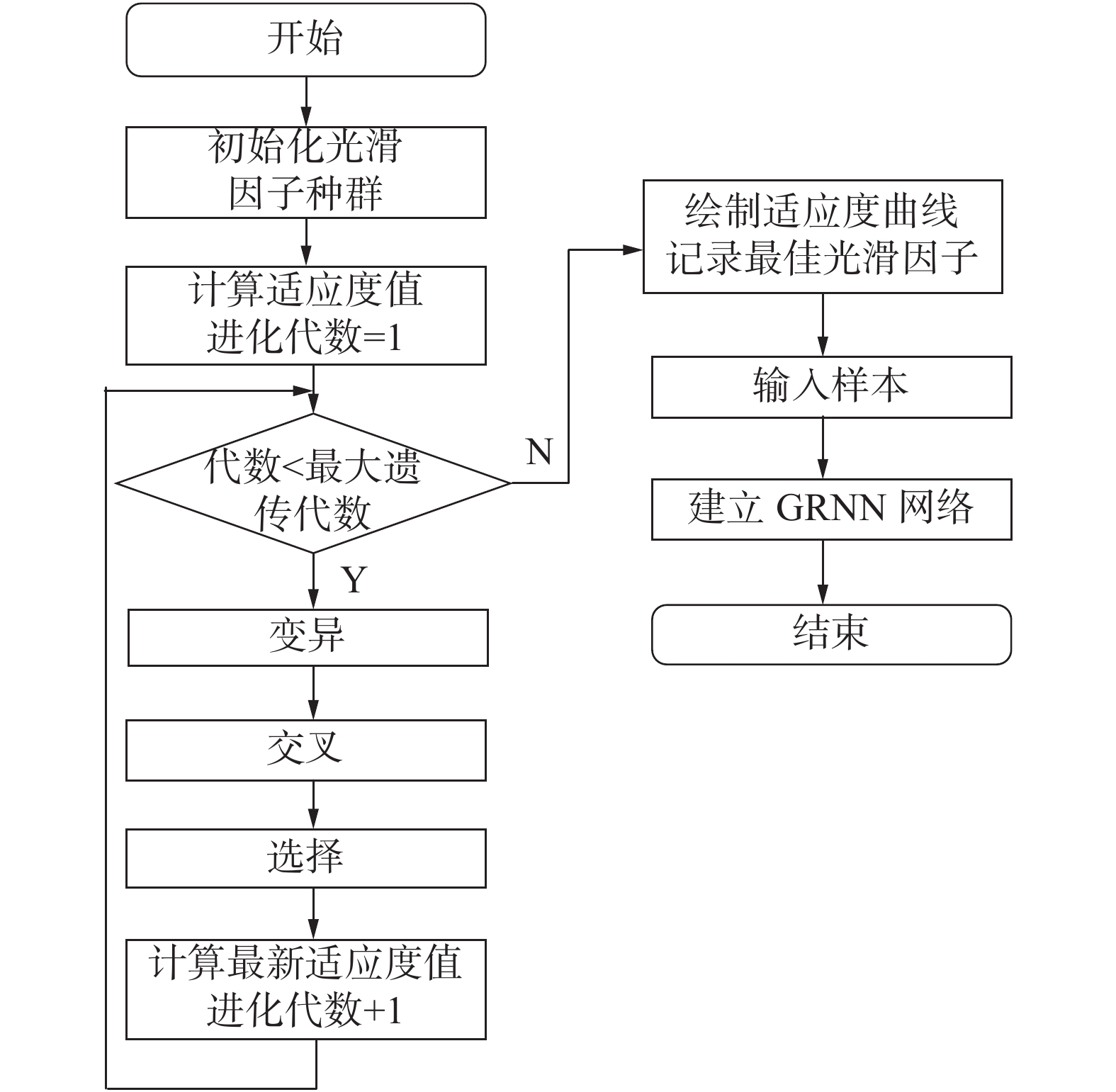
设DE的种群规模为50，最大迭代次数为12，变异概率为0.09，交叉概率为0.9，操作精度为0.000 01，当迭代次数达到设定的的最大值，将得到的最优扩展常数即光滑因子带入GRNN，实现布里渊散射谱的拟合。混合优化算法流程图如图2所示。

2 仿真分析

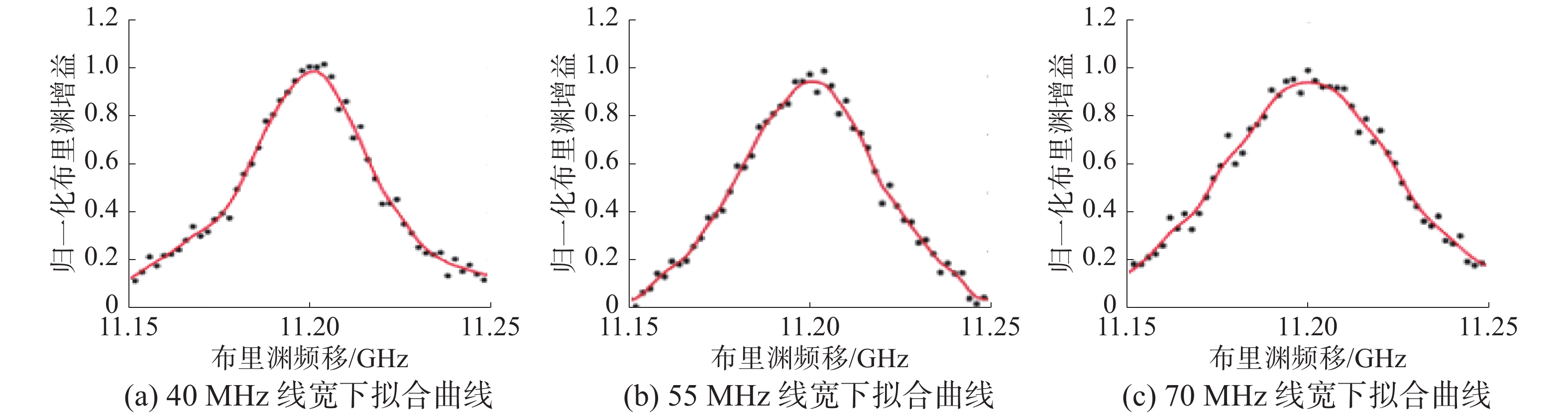
由式（1）可以得到数值仿真所需的布里渊散射谱。假设布里渊中心频移 ${v_B}$ 为11.2 GHz，权重比 $k$ 为0.9，利用均方根误差（root-mean-square error, RMSE）、平均绝对偏差（mean absolute deviation, MAD）及拟合度（ ${R^2}$ ）评估DE−GRNN算法在不同线宽和不同 ${R_{{\rm{SN}}}}$ 下的拟合性能。在 ${R_{{\rm{SN}}}}$ 为30 dB，线宽分别为40、55、70 MHz条件下，混合优化算法布里渊散射谱特征提取仿真如图3所示。在线宽为40 MHz， ${R_{{\rm{SN}}}}$ 分别为10、20、30 dB情况下，混合优化算法布里渊散射谱特征提取如图4所示。对不同 ${R_{{\rm{SN}}}}$ 及线宽的仿真结果如表1所示。

由图3、4及表1可以看出，在不同 ${R_{{\rm{SN}}}}$ 和不同线宽情况下，本文所提出的混合优化算法可以实现对布里渊散射谱的拟合，在权重比 $k$ =0.9、 ${R_{{\rm{SN}}}}$ =30 dB、线宽40 MHz的情况下，最佳 ${R^2}$ 值可达0.998 3，最小RMSE为0.012 0，最小MAD为0.010 1。2016年，张燕君等^[18]比较了在同样条件下粒子群优化算法（particle swarm optimization，PSO）、量子粒子群优化算法（quantum particle swarm optimization，QPSO）、遗传算法结合粒子群算法（genetic algorithm and particle swarm optimization，GAPSO）、莱文伯−马夸特算法结合粒子群优化算法（Levenberg−Marquardt and particle swarm optimization，LM-PSO）算法和遗传算法结合量子粒子群优化算法（genetic algorithm and quantum particle swarm optimization，GA−QPSO）算法对布里渊散射谱的拟合性能，相应的拟合度 ${R^2}$ 分别为0.839 3、0.952 1、0.971 9、0.974 1、0.991 3。因此，本文提出的算法可以实现更高精度提取布里渊散射谱特征，误差小，具有实际应用前景。

3 结论

提出一种DE-GRNN的混合优化算法，利用DE算法对GRNN的光滑因子自动寻优，由仿真实验结果可以得到以下结论：

1）该混合优化算法可以实现不同信噪比和不同线宽情况下布里渊散射谱的曲线拟合，最优拟合度达0.998 3，最小均方根误差为0.012 0，最小平均绝对误差为0.010 1；

2）相较于传统PSO、QPSO、GAPSO、LM-PSO和GA-QPSO，布里渊散射谱拟合算法，具有更高的拟合度；

3）同时，该算法不依赖初值，避免了传统算法易陷入局部极值的弊端，对于BOTDA型分布式光纤传感系统的布里渊散射谱拟合，提高分布式光纤传感器故障点检测精度具有重要实际意义。

在低信噪比的情况下，本文算法的布里渊散射谱拟合度相对较低，仍需进一步提升拟合性能，以适应噪声干扰较大情况下的布里渊散射谱特征提取。