现代战争中，信息战日渐成为战争中的重要部分。MIMO技术可以在不增加频谱资源和天线发射功率的情况下，成倍提高系统容量和链路可靠性，是现代无线通信的重大突破，也是军用通信系统最有可能采用的方案^[1−2]。文献[3−5]在Simulink环境下研究了常规FH系统在多种人为干扰下的传输性能，FH技术对系统抗干扰性能有显著提升，但单发单收系统传信速率和信道容量的局限性，不能适用于未来大规模军用通信；文献[6]提出了一种新的数学模型，并结合正交频分复用（orthogonal frequency division multiplexing，OFDM）技术实现了Alamouti发射分集结构系统下的多载波、多天线传输，提升了系统的灵活性和可靠性，但系统仅考虑了内部参数变化对性能的影响，并未针对系统抗干扰性能进行研究且MIMO规模十分有限；文献[7−10]将空时分组码在正交设计的理论上把Alamouti空时码从两副发射天线推广到多副发射天线系统；文献[11]提出了一种基于国内外普通军用跳频移频键控（frequency-hopping frequency-shift keying，FH−FSK）和空时移频键控（space-time frequency-shift keying，ST−FSK）技术的跳频空时移频键控（frequency-hopping space-time frequency-shift keying, FH−ST−FSK）数据通信系统模型，并对2发1收ST−FSK系统在加性高斯白噪声和慢衰落信道下的性能进行初步仿真，相比于普通FSK系统有更强的抗衰落和抗干扰能力，但FH−ST−FSK模型只适用于一发多收系统或多发一收系统，且仅限于理论模型尚未仿真实现；文献[12]提出了一种基于空时分组编码（space-time block coding，STBC）和空时跳频(space-time frequency-hopping, SFH)技术的多天线跳频抗干扰的SFH−STBC系统基本理论模型，在Simulink环境下仿真了2发2收SFH−STBC系统在衰落信道和多种人为干扰下的性能，系统抗干扰性能提升显著，但其对译码部分并未给出具体推导，且仅针对Alamouti结构系统，并未将此模型具体实现到多天线SFH−STBC系统中。

1 STFH−MIMO系统模型

本文分别提出了STFH编码算法和相应的OCF译码算法，并基于此在MIMO通信环境下设计了全新的STFH−MIMO系统，并在多种人为干扰下进行仿真验证。仿真结果表明，相比于传统STBC系统和FH系统，该方案通信性能及抗干扰效果显著，更适用于未来军用通信。

STFH−MIMO系统在发送端利用STFH算法将MFSK调制信号进行STBC编码并由MIMO天线阵列加载到10~20 GHz高频段跳频发送，信道中加入自然噪声和人为干扰，接收端利用OCF算法译码恢复发送信息。

本系统具体含8个模块，即信号调制模块、STBC模块、STFH模块、信道传输模块、跳频同步模块、OCF译码模块、下变频模块、信号解调模块。其中STFH编码算法和OCF译码算法由整体系统中的部分模块构成。

调制模块将基带信号调制到载波，采取的调制方式为MFSK。接收端采取非相干方式解调。

STFH算法实现编码，主要包括STBC模块和上变频模块。STBC模块采用8发8收STBC复矩阵编码，以获得时间分集和空间分集增益；上变频模块实现STBC信号在10~20 GHz频段的跳频传输。

OCF算法实现译码，主要包括跳频同步模块、STBC译码模块和下变频模块。跳频同步模块可获取系统发送端跳频图案；STBC译码模块实现不同时刻信号的分离和载波相干；下变频模块实现跳频载波消除，最终恢复发送信号。

跳频序列生成模块通过m序列，使用非连续抽头模型生成跳频图案，生成的跳频序列具有良好的汉明相关性能。跳频同步模块采用同步字头法，定频发送同步消息，定频数为4。同步字头中含有跳频序列全部信息，接收机依照同步信息实现跳频同步。

信道传输模块采用瑞利信道，信道中包含自然噪声和人为干扰。自然噪声随机生成，干扰信号则选取3种典型形式加入通信接收方的信号中，以验证STFH-MIMO系统抗干扰性能。

2 STFH编码算法和OCF译码算法 2.1 STFH编码算法

m(t)为输入信息码序列{1，0，0，1，…}， $m(t)$ 通过多进制频移键控(multiple frequency-shift keying, MFSK)调制后得到频带宽度为 ${R_B}$ 的调制信号 $s(t)$ ：

$ \begin{array}{l} s\left( t \right) = {A_0}\cos \left[ {\left( {{\omega _{b0}} \pm i\Delta {\omega _b}} \right)t} \right] = {A_0}\cos \left[ {\left( {{\omega _{b0}} \pm in {\text {π}} {R_B}} \right)t} \right] \end{array} $

式中： ${A_0}$ 是幅度； $n$ 为正整数； ${\omega _{{b_0}}}$ 为MFSK信号载波起始频率； $\Delta {\omega _{{b_0}}}$ 为频率间隔；i=1, 2, …, M/2。

调制后对信号 $s(t)$ 进行STBC编码，目的是为了获得分集增益，提高频谱利用率，提高信息传输准确率。假设发射天线总数为 $M$ ，接收天线总数为 $N$ ，MFSK信号经过STBC编码后得到信号 ${s_{0_i}}\left( t \right)\left( {i = 1,2,\cdots, M} \right)$ 。

跳频序列由独立产生的伪随机码产生，频率合成器由跳频序列控制，频率合成器的输出频率按照不同的跳频图案或者指令随机地变化。

信号 ${s_{0_i}}\left( t \right)$ 经过频率合成器上变频得到跳频信号 ${s_{{T_i}}}\left( t \right)$ ，可表示为：

${s_{{T_i}}}\left( t \right){\rm{ = }}{s_{0_i}}\left( t \right)\cos \left[ {\left( {{\omega _0} + {\omega _n}} \right)t + {\phi _n}} \right]$

式中： ${T_i}$ 表示第 $i$ 根发射天线的发射信号； $\cos \left[ {\left( {{\omega _0} + {\omega _n}} \right)t + {\phi _n}} \right]$ 为由跳频序列生成的跳频载波，其中 ${\omega _n} = k\Delta \omega $ ， $\Delta \omega$ 为跳频频率间隔， $k$ 为最终生成的跳频频率序列控制系数，M根发射天线对应的 $M$ 组行向量STBC信号分别与跳频序列上变频混频后发射； ${\omega _0}$ 为10~20 GHz频段上跳频载波的起始设置频率； ${\phi _n}$ 为频率合成器输出信号的频率和初相。

STFH−MIMO系统接收端第 $i$ 根天线在第 $j$ 时刻接收到的信号 ${s_{R_{ij}}}\left( t \right)$ 为：

$ \begin{array}{l} {s_{R_{ij}}}\left( t \right) = \left[ {\sum\limits_{i = 1}^M {{s_{T_{ij}}}\left( t \right)} } \right] + \left[ {{j_{ij}}\left( t \right) + {n_{ij}}\left( t \right)} \right] \end{array} $

式中：M代表发送天线的总根数， $N$ 代表接收天线的总根数； ${n_{j}}\left( t \right)$ 表示 $j$ 时刻的信道噪声； ${j_{i}}\left( t \right)$ 表示第 $i$ 根天线受到的干扰；i = 1, 2, … M; j = 1, 2, …, 2N。

2.2 OCF译码算法

假定MIMO天线阵列规模为8×8，其中设定各发射天线采用同一跳频图案，STBC采用8×16复数矩阵，设定16个时刻为一个时隙，每跳传输数据个数为z=16T（T表示倍数），则任意一组STBC矩阵中任一天线在任一时隙的16位数据必在同一跳频频率下传输，即任一跳频点下的数据传输都相互独立。

${X_8} = \left[ {{X_{8, {\rm real}}}\;\;\;\; {\rm conj}\left( {{X_{8, {\rm real}}}} \right)} \right]$

式中： ${X_{\rm 8,real}}$ 是8×8天线阵列的实编码矩阵； ${X_8}$ 是复数编码矩阵。

为了便于研究分析，本文首先考虑一根接收天线的解码情况，任选跳频频点 $f$ 下一组STBC信号译码进行数学推导：

$ \begin{aligned} & \left[ {{R_1}\;\;{R_2}\;\; \cdots \;\;{R_{16}}} \right] = \sqrt {\frac{{{E_x}}}{{8{N_0}}}} {\left[ {{h_1}\;\;{h_2}\;\; \cdots \;\;{h_8}} \right]} \cdot \\ & \quad \quad \left\lfloor {\left[ {{X_{8, {\rm real}}}\;\;\;\; {\rm conj}\left( {{X_{8, {\rm real}}}} \right)} \right] \cdot G} \right\rfloor + \left[ {{z_1}\;\;{z_2}\;\; \cdots \;\;{z_{16}}} \right] \end{aligned} $

式中： ${R_j}$ 是接收信号； ${h_i}$ 是信道传输系数； ${E_x}$ 是每根发射天线的平均能量； ${N_0}$ 是复高斯白噪声的功率； $ \odot $ 表示哈达玛乘积，其运算规则为矩阵元素对应相乘；z_j= J_j+n_j,j = 1, 2, 3, …, 2N。

跳频载波序列G为：

$ { G}{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {\cos \left( {2{\text π} f{t_1}} \right)}\;\;\; {\cos \left( {2{\text π} f{t_2}} \right)}& { \cdots } & {\cos \left( {2{\text π} f{t_{16}}} \right)}\\ {\cos \left( {2{\text π} f{t_1}} \right)} \;\;\;{\cos \left( {2{\text π} f{t_2}} \right)}& { \cdots } & {\cos \left( {2{\text π} f{t_{16}}} \right)}\\ {\vdots} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; { \cdots } & { \cdots } & { \cdots }\\ {\cos \left( {2{\text π} f{t_1}} \right)} \;\;\; {\cos \left( {2{\text π} f{t_1}} \right)}& { \cdots } & {\cos \left( {2{\text π} f{t_{16}}} \right)} \end{array}} \right]_{8*16}} $

$ {{ R}_{\rm eff}} = \sqrt {\frac{{{E_x}}}{{8{N_0}}}} \left[ {{{ H}_{\rm eff}} \odot {{ G}^H}} \right]{{ x}_{\rm eff}} + {{ z}_{\rm eff}} $

式中：接收信号 ${{ R}_{\rm eff}} = {\left[ {{R_1}\;\; \cdots \;\;{R_8}\;\;R_9^*\;\; \cdots \;\;R_{16}^*} \right]^{\rm T}}$ ；信道系数 ${{ H}_{\rm eff}}{\rm{ = }}\left[ \begin{array}{l}{H_c}\\{\rm conj}\left( {{H_c}} \right)\end{array} \right]$ ； ${H_c}$ 是8×8天线阵列的复信道矩阵；发送信息为 ${{ x}_{eff}} = {\left[ {{x_1}\;\;{x_2}\;\;{x_3}\;\;{x_4}\;\;{x_5}\;\;{x_6}\;\;{x_7}\;\;{x_8}} \right]^{\rm T}}$ ；信道干扰及噪声为 ${{ z}_{\rm eff}} = {\left[ {{z_1}\;\; \cdots \;\;{z_8}\;\;z_9^*\;\; \cdots \;\;z_{16}^*} \right]^{\rm T}}$ 。

$ \begin{aligned} {{\tilde { R}}_{\rm eff}} = & {\left[ {{{ H}_{\rm eff}} \odot {{ G}^{\rm H}}} \right]^{\rm H}}*{{ R}_{\rm eff}} = \left[ {{ H}_{\rm eff}^{\rm H} \odot { G}} \right]*{{ R}_{\rm eff}}{\rm{ = }}\\ & \sqrt {\frac{{{E_x}}}{{8{N_0}}}} \left[ {{ H}_{\rm eff}^{ H} \odot { G}} \right]\left[ {{{ H}_{\rm eff}} \odot {{ G}^{\rm H}}} \right]{{ x}_{\rm eff}} + \left[ {{ H}_{\rm eff}^{\rm H} \odot { G}} \right]{{ z}_{\rm eff}} = \\ & \sqrt {\frac{{{E_x}}}{{8{N_0}}}} \left[ {{\rm H}_{\rm eff}^{ H} \odot { G}} \right]\left[ {{{ H}_{\rm eff}} \odot {{ G}^{\rm H}}} \right]{{ x}_{\rm eff}} + {{\tilde { z}}_{\rm eff}} \end{aligned} $

接收信号 ${{\tilde { R}}_{\rm eff}}$ 经过低通滤波后得到：

${{\tilde { R}}_{\rm eff}} = \sqrt {\frac{{{E_x}}}{{8{N_0}}}} \sum\limits_{i = 1}^8 {{{\left| {{h_i}} \right|}^2}{{ I}_8}{{ x}_{\rm eff}} + {{\tilde { z}}_{\rm eff}}} $

式中 ${{ I}_8}$ 为8阶单位矩阵。

对滤波后的接收信号经过补偿得到：

${{\tilde { R}}_{\rm eff}} = \sqrt {\frac{{{E_x}}}{{2{N_0}}}} \sum\limits_{i = 1}^8 {{{\left| {{h_i}} \right|}^2}{{ I}_8}{{ x}_{\rm eff}} + {{\tilde { z}}_{\rm eff}}} $

对于多根接收天线的解码，利用上述OCF译码算法对每根接收天线接收信号独立地进行解码，然后将各天线解码信号进行叠加，即可得到在跳频载波 $f$ 下发送的全部天线接收到的信息。

3 仿真结果与分析

本文在MATLAB8.0下完成在下行链路移动通信环境中对STFH−MIMO系统的仿真，编写程序完成各个模块数学模型的建立，按照执行流程将各个模块连接起来。加入3种不同的干扰模式并改变相应的仿真参数，在10~20 GHz高频段改变信噪比，分析不同MIMO规模下的STFH-MIMO通信系统的误码率，评价系统抗干扰性能。本系统中跳频增益设置约为12 dB。

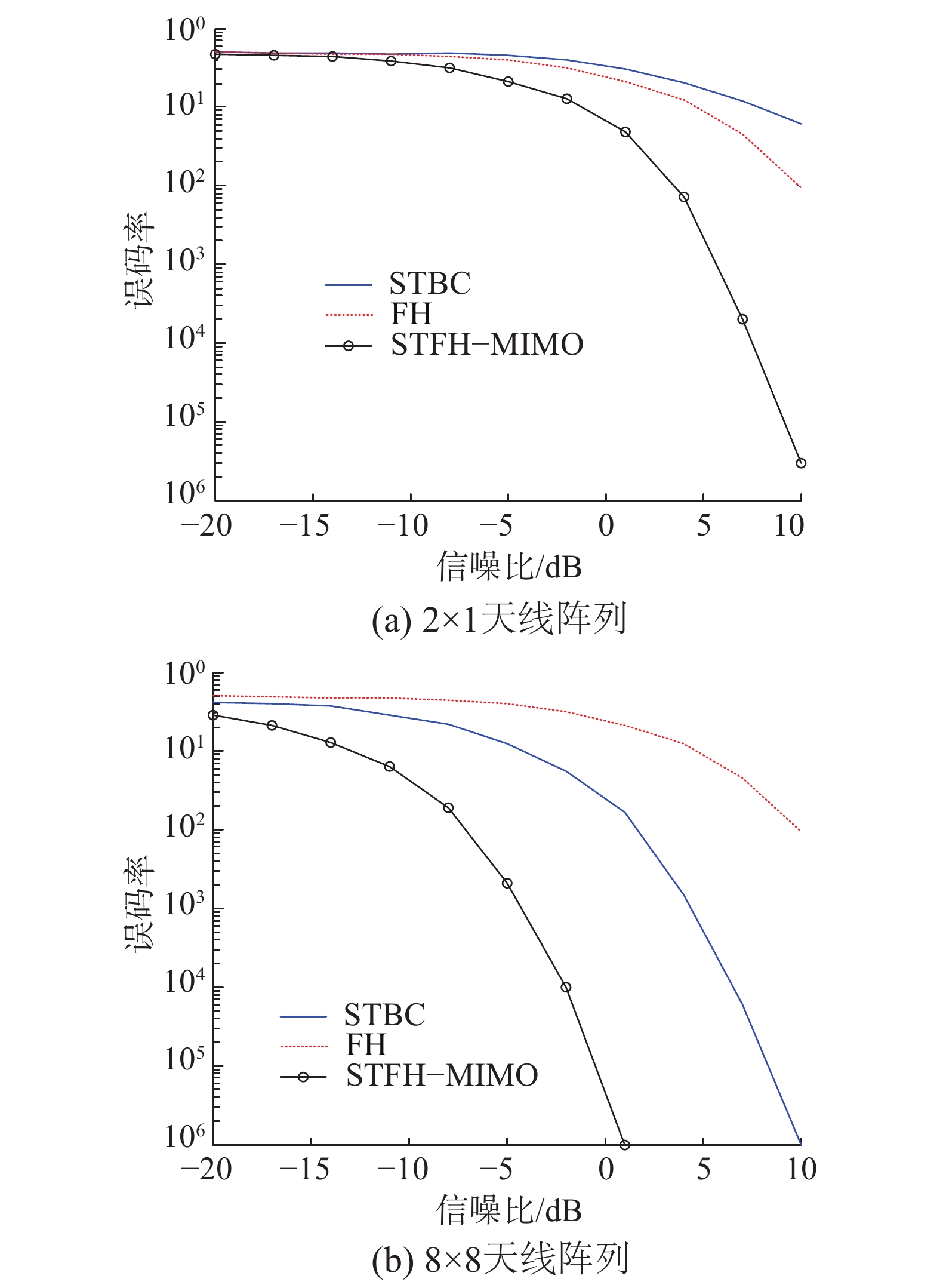
3.1 宽带干扰仿真结果与分析

宽带阻塞干扰下STBC系统、FH系统和STFH-MIMO系统的误码率曲线如图1所示，其中调制方式为2FSK。

从图1中可以看出：

1）在任一种天线规模中，相比于其他2种系统，STFH−MIMO系统在宽带干扰下的抗干扰性能优势均很明显；

2）在同等天线规模中，相比之下STFH−MIMO系统的性能优势明显。在2×1和8×8规模的天线阵列中，在误码率同为 ${P_e} = {10^{{\rm{ - }}1}}$ 处时，STFH−MIMO系统相比于STBC系统均有大约为10 dB的增益，说明跳频给系统带来10 dB增益；

3）在天线规模确定的情况下，在误码率为 ${P_e} = {10^{{\rm{ - }}1}}$ 处，2×1/STFH−MIMO系统相比于FH系统增益为6 dB；在8×8天线阵列中相比于FH系统增益为18 dB，说明天线规模从单发单收增加到2发1收，STBC分集复用增益为6 dB；从单发单收增加到8发8收，STBC分集复用增益为18 dB。

3.2 部分频带干扰仿真结果与分析

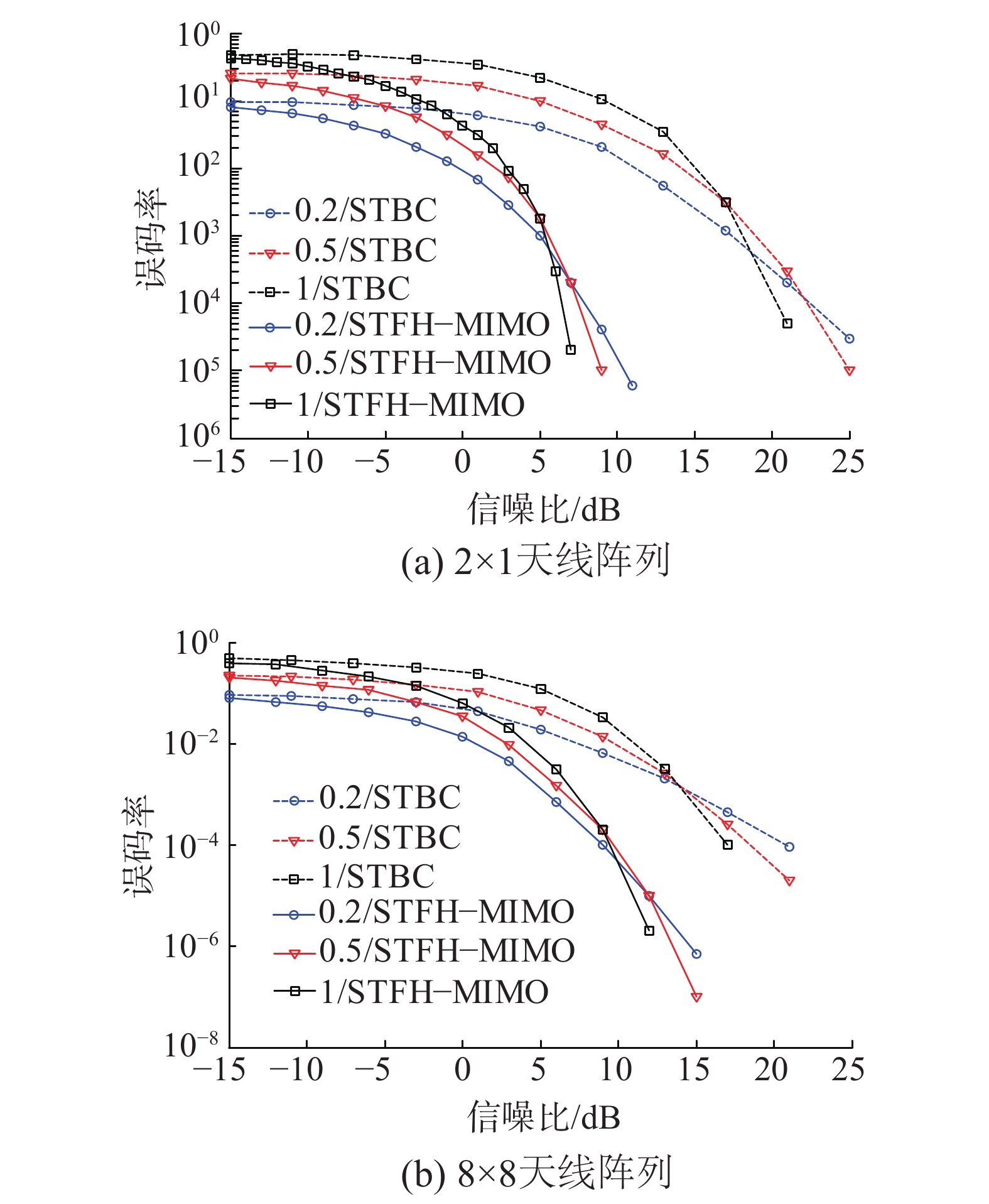
部分频带干扰下STBC系统和STFH−MIMO系统的误码率曲线如图2所示，其中调制方式为2FSK。设置干扰因子 $\rho $ 为部分频带干扰信号覆盖跳频信号的程度。

从图2中可以看出：

1）在干扰系数 $\rho $ 和天线规模确定的情况下，STFH−MIMO系统与STBC系统之间的性能差别在于跳频增益。在误码率为 ${P_e} = {10^{{\rm{ - }}1}}$ 处时，系统跳频增益均在10 dB上下浮动，说明跳频增益为10 dB，这与宽带干扰是相符合的；在干扰系数 $\rho $ 确定的情况下，在误码率同为 ${P_e} = {10^{{\rm{ - }}1}}$ 处时，天线规模由2×1阵列增加至8×8阵列，STFH−MIMO系统和STBC系统均有大约12 dB的增益，说明STBC分集技术带来了12 dB的分集增益，这也与宽带干扰下一致；

2）在同一规模天线阵列下，无论STBC系统还是STFH−MIMO系统中，存在共同的规律，即当 $\rho {\rm{ = }}0.2$ 时，误码率不会超过 0.1；当 $\rho {\rm{ = }}0.5$ 时，误码率不会超过0.25；当 $\rho {\rm{ = }}1$ 时，误码率不会超过0.5，此时已达到最坏；

3）当信噪比很大时， $\rho {\rm{ = }}0.2$ 时的干扰效果最好；当信噪比很小时， $\rho {\rm{ = 1}}$ 时的干扰效果最好。出现这种情况是因为，在低信噪比情况下，噪声功率相对较高，平均到干扰频带后，在特定频点的干扰功率依然很高，故需要增大干扰因子采取大范围频率段覆盖干扰使效果更好；在高信噪比情况下，噪声功率相对较低，平均到干扰频带后，特定频点上的干扰功率不足以对跳频信号产生干扰，故需要降低干扰因子集中能量干扰某一小段频率，期望达到较好的干扰效果。

以上分析表明跳频通信系统在部分频带干扰下，性能并不是干扰因子最小或最大就是最佳。

3.3 跟踪干扰仿真结果与分析

跟踪干扰下STFH−MIMO系统的误码率曲线如图3所示，其中调制方式为2FSK。设置干扰因子 $\rho $ 为干扰信号跟踪跳频频点时间与跳频信号跳变时间之比。

从图3中可以看出：

1）在天线规模和干扰系数 $\rho $ 确定的情况下，在误码率同为 ${P_e} = {10^{{\rm{ - }}1}}$ 处时，STFH−MIMO系统由于FH技术的应用，抗干扰性能相比于STBC系统均有大约10 dB的明显提升，即跳频增益大约为10 dB，这与之前的仿真结果是一致的；

2）随着天线规模增加，在干扰系数 $\rho $ 确定的情况下，在误码率同为 ${P_e} = {10^{{\rm{ - }}1}}$ 处时，STBC系统和STFH−MIMO系统的抗跟踪干扰性能均有大约12 dB的提升，说明天线规模由2×1扩大到8×8对抵抗跟踪干扰起到了很大的作用；

3）跟踪干扰要比宽带干扰和部分频带干扰强得多。在天线规模确定的情况下，STBC系统和STFH−MIMO系统， $\rho {\rm{ = }}0.2$ 时干扰效果最差， $\rho {\rm{ = }}1$ 时干扰效果最好。即随着跟踪因子 $\rho $ 的增加，误码率均直线上升，干扰效果越来越好。从信噪比大小可以看出，跳频通信系统增益已经对跟踪干扰信号完全失去作用。

4 结论

1）本文分别提出了STFH编码算法和OCF译码算法，并基于此设计STFH−MIMO通信系统进行仿真并验证算法可靠性。其中STFH算法通过MIMO技术和FH技术实现了信息的空时频分集，同时获得了分集复用增益和跳频增益，提高频谱利用率的同时进一步提升了抗干扰性能；OCF算法译码复杂度低，并能有效消除信息中的跳频载波分量，确保STBC信号跳频传输的优越性能。

2）为进一步验证系统抗干扰性能，在3种典型干扰环境下将STFH−MIMO系统与常规STBC系统、FH系统对比。仿真发现STBC分集技术和FH技术均有不同程度的抗干扰能力，低规模MIMO下FH技术抗干扰性能显著，跳频增益约为10 dB，但跳频增益受带宽限制；而随着天线规模增加STBC分集增益随之增加，抗干扰效果愈加显著，天线规模从单发单收FH系统增加到8×8/STFH−MIMO系统可得STBC分集复用增益约18 dB。同时3种干扰中跟踪干扰能力最强，对系统具有毁灭性影响。

3）跟踪干扰是常规跳频通信的克星，能够对跳频通信系统造成最佳干扰；但也存在不足之处，受到多方面的约束，如跳频系统跳速和干扰跳速、有用信号功率和干扰信号功率、通信信号传输时延和干扰信号传输时延、跳频系统带宽和干扰机带宽等。被干扰方可根据这些前提，采取相应的措施克制跟踪干扰。

4）STFH−MIMO通信系统工作在10~20 GHz高频段，具有通信性能好、频谱利用率高、抗干扰性强等优点，此外还具有更高的传输速率和更大的信道容量，适应于未来军用通信。