盲源分离是一种通信信号处理技术,指在信号的理论模型和信号无法精确获知的情况下,从若干混叠信号中分离出无法直接观测的源信号的过程[1]。它最早起源于“鸡尾酒会”中嘈杂环境下的语音提取问题。随着几十年来的发展,该技术的研究拓展到众多领域,在语音识别、图像处理、无线通信、生物医学等众多领域都具有广泛的应用前景[2−5]。
欠定盲源分离是观测信号数量少于源信号数量条件下的盲源分离问题,在信号处理问题上满足实际环境需求。研究欠定盲源分离问题,主要是基于稀疏分量分析方法的混合矩阵估计和源信号恢复。FCM聚类算法是一种常见的聚类算法,具有数据划分详细、归类精准的优点,但在隶属度的选取方式中存在数据归类慢的缺陷,这在一定程度上影响着聚类效果[6−7]。针对这一缺陷,本文采用指数形式修正因子,对隶属度划分方式进行优化,并将改进后的算法用于语音分离实验。改进后的算法,在提升混合矩阵的估计精度的同时,还改善了算法的收敛速度。
1 盲源分离问题描述下面将以常见的线性瞬时混合信号分离为主,对盲源分离的系统模型和理论方法进行描述。
1.1 盲源分离系统模型盲源分离的线性瞬时混合模型如图1所示。

|
Download:
|
| 图 1 盲源分离基本模型 | |
由图1可知,盲源分离系统主要由混合系统模型和分离系统模型组成,混合系统对应的数学表达式为
| ${X}(t) = {AS}(t) + {N}(t)$ |
式中:
| ${Y}(t) = {WX}(t)$ |
式中
实际应用中,根据盲信号分离中源信号数目
混合信号分离前,首先要进行信号的预处理,这个步骤很重要,可以减少算法的计算量,增加信号分离效率。
1.2.1 信号初始化这里对观测信号的初始化是对观测信号样点进行单位化和对称化的初始工作。对于任何一个观测信号向量
| ${\overset{\frown} {{X}}} (t) = \left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{X}(t)}}{{\left\| {{X}(t)} \right\|}},}&{{x_k}(t) \geqslant 0} \\ { - \displaystyle\frac{{{X}(t)}}{{\left\| {{X}(t)} \right\|}},}&{{x_k}(t) < 0} \end{array}} \right.$ | (1) |
根据信号在时域或变换域上散点图的线性聚类特性,混合矩阵的一个列向量与散点图中一条直线的方向共线。一般情况下,混合矩阵列矢量方向往往与观测信号能量集中的数据点方向一致,而一些能量较分散的数据点不仅对估计混合矩阵列向量贡献不大,反而会造成干扰[8]。因此,有必要去除这些无用的边缘能量时频点,提高混合矩阵的估计精度。判定某一时频点是否为能量集中点的公式为
| $\left\| {{X}(t,f)} \right\| > \rho \cdot \max \left\| {{X}(t,f)} \right\|$ |
式中
稀疏成分分析是借助源信号的稀疏特性来实现盲源分离。它充分利用了混合信号具有的稀疏性来提取源信号的特征,以较高的精度重构出源信号,成为非常重要且热门的欠定盲源分离方法[9]。稀疏成分分析算法用于欠定盲源分离问题中的具体步骤如下:
1)获取观测信号,选取最合适的时频变换工具,实现最优的稀疏变换,使得信号在变换域内尽量稀疏;
2)信号在稀疏域中,散点图出现线性聚类的情况,即呈现方向性,使用聚类法、势函数法等准确地估计混合矩阵;
3)混合矩阵估计结束后,利用如线性规划法、压缩感知法等实现源信号的恢复,最后将源信号由变换域恢复到时域即可。
2 混合矩阵估计算法 2.1 模糊C均值(FCM)算法FCM算法是一种基于目标函数的模糊聚类算法,该算法具体内容描述为:设
| $\sum\limits_{i = 1}^c {{u_{ij}}} = 1,{u_{ij}} \geqslant 0$ |
由上面的成分构成的FCM聚类目标函数为[10]:
| $J\left( {{U},{P}} \right) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {{u_{ij}}^m{{\left\| {{x_j} - {p_i}} \right\|}^2}} } $ | (2) |
式中:
当目标函数满足约束条件时,利用拉格朗日函数构造求得分类矩阵与聚类中心的迭代表达式,再通过多次迭代计算,得到目标函数的全局最小值,也是最优的聚类结果。
FCM算法步骤如下:
1):参数初始化。包括加权指数
2)更新分类矩阵
| ${u_{ij}}^{\left( l \right)} = {\left( {\displaystyle\sum\limits_{k = 1}^c {{{\left( {\displaystyle\frac{{\left\| {{x_j} - {p_i}^{\left( l \right)}} \right\|}}{{\left\| {{x_j} - {p_k}^{\left( l \right)}} \right\|}}} \right)}^{\frac{2}{{m - 1}}}}} } \right)^{ - 1}}$ | (3) |
| ${p_i}^{\left( {l + 1} \right)} = \displaystyle\frac{{\displaystyle\sum\limits_{j = 1}^n {{{\left( {{u_{ij}}^{\left( {l + 1} \right)}} \right)}^m}} {x_j}}}{{\displaystyle\sum\limits_{j = 1}^n {{{\left( {{u_{ij}}^{\left( {l + 1} \right)}} \right)}^m}} }}$ | (4) |
3)计算到相邻2次目标函数之差小于规定的阈值或者迭代次数达到最大值的时候,即满足
隶属度在FCM算法中是一个非常重要的概念,表示样本点属于聚类中心的程度[11]。本节将说明利用指数形式修正因子,优化隶属度划分方式的原理。
1)将式(2)的FCM聚类目标函数改写为
| $J'\left( {{U},{P}} \right) = \displaystyle\sum\limits_{i = 1}^c {\displaystyle\sum\limits_{j = 1}^n {{u_{ij}}^m} } {d^2}\left( {{x_j},{p_i}} \right) + \displaystyle\sum\limits_{i = 1}^c {\displaystyle\sum\limits_{j = 1}^n {{b_j}{u_{ij}}\left( {1 - {u_{ij}}^{m - 1}} \right)} } $ | (5) |
式(2)与式(5)的区别在于式(5)多出了一组求和项,也是在式(2)基础上增加的优化项,其核心优化系数为
| ${b_j} = {b^{\left| {s - 1} \right|}} \cdot \min \left\{ {{d^2}\left( {{x_j},{p_s}} \right)\left| {s \in \left\{ {1,2, \cdots ,c} \right\}} \right.} \right\}$ | (6) |
样本点与类中心的隶属度越大(小),说明该样本点属于该类中心的可能性越大(小)[12]。所以,设定中心点位置具有高隶属度,其他点隶属度较低,以此提高分类准确性。针对优化目标,采用指数形式修正因子,是利用其函数变化速率快的特点来加快数据点的归类速度。假设xj对
| ${u_{1j}} > {u_{2j}} > \cdots > {u_{cj}}$ |
那么式(6)中的指数函数
2)利用Lagrange函数构造目标函数,然后分别对
| $\displaystyle\frac{{\partial J}}{{\partial {u_{ij}}}} = m{\left\| {{x_j} - {p_i}} \right\|^2}{u_{ij}}^{m - 1} + {\lambda _j} + {b_j} - m{b_j}{u_{ij}}^{m - 1} = 0$ |
| $\frac{{\partial J}}{{\partial {p_i}}} = \displaystyle\sum\limits_{j = 1}^n {2{u_{ij}}^m\left( {{x_j} - {p_i}} \right)} = 0$ |
根据约束条件,求得方程的根,即分类矩阵与聚类中心的迭代表达式。
| ${u_{ij}} = \displaystyle\frac{1}{{{{\displaystyle\sum\limits_{k = 1}^c {\left( {\displaystyle\frac{{{d^2}\left( {{x_j},{p_i}} \right) - {b^{\left| {s - 1} \right|}} \cdot {{\min }_{1 \leqslant s \leqslant c}}{d^2}\left( {{x_j},{p_s}} \right)}}{{{d^2}\left( {{x_j},{p_k}} \right) - {b^{\left| {s - 1} \right|}} \cdot {{\min }_{1 \leqslant s \leqslant c}}{d^2}\left( {{x_j},{p_s}} \right)}}} \right)} }^{\frac{1}{{m - 1}}}}}}$ |
| ${p_i} = \displaystyle\frac{{\displaystyle\sum\limits_{j = 1}^n {{u_{ij}}^m} {x_j}}}{{\displaystyle\sum\limits_{j = 1}^n {{u_{ij}}^m} }}$ |
3)遵循传统FCM算法的步骤,完成分类矩阵
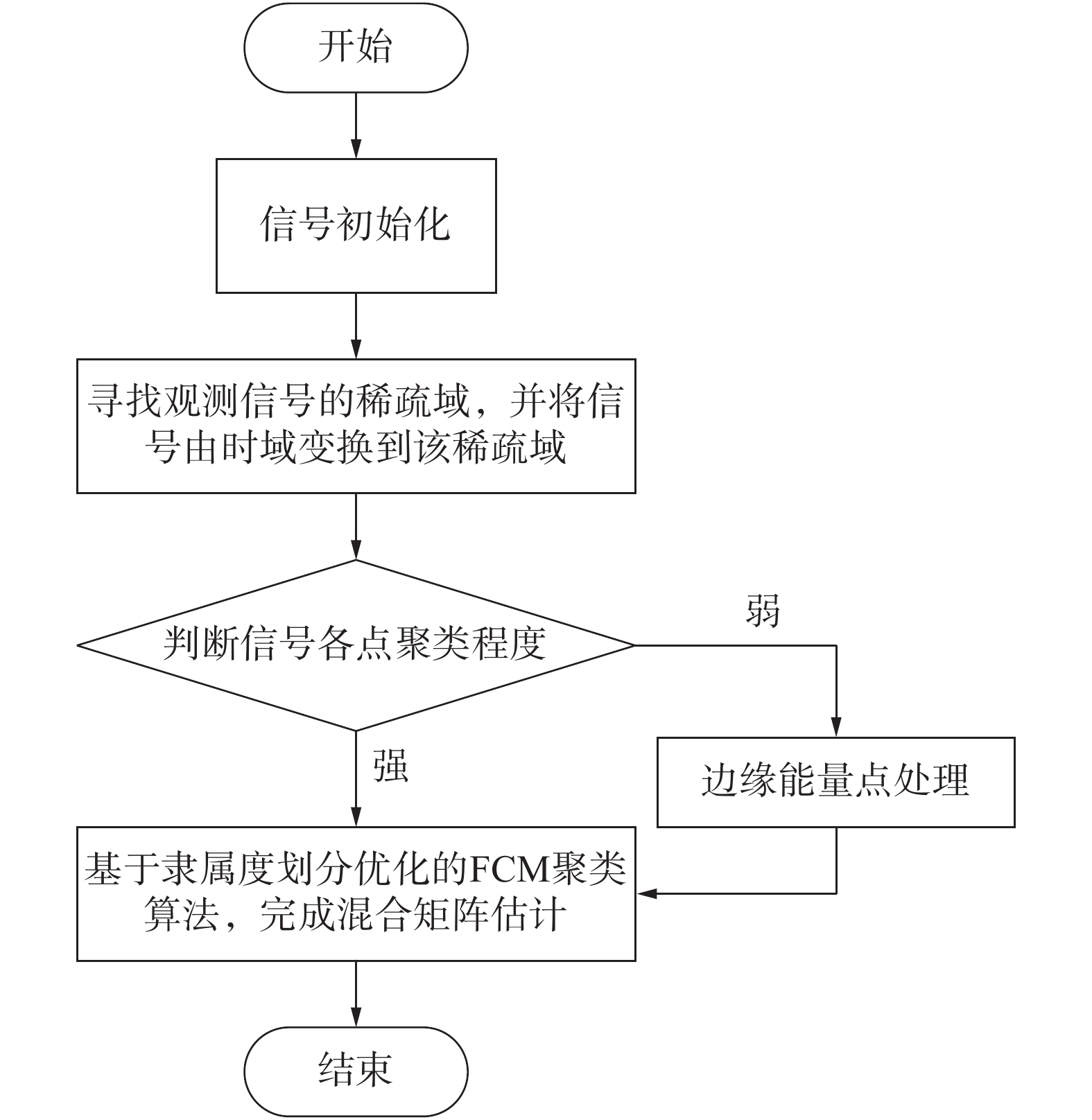
实现混合矩阵估计的整个流程如图2所示。
|
Download:
|
| 图 2 实现混合矩阵估计的流程 | |
为验证算法的性能,我们通过语音信号的盲源分离仿真实验来完成。
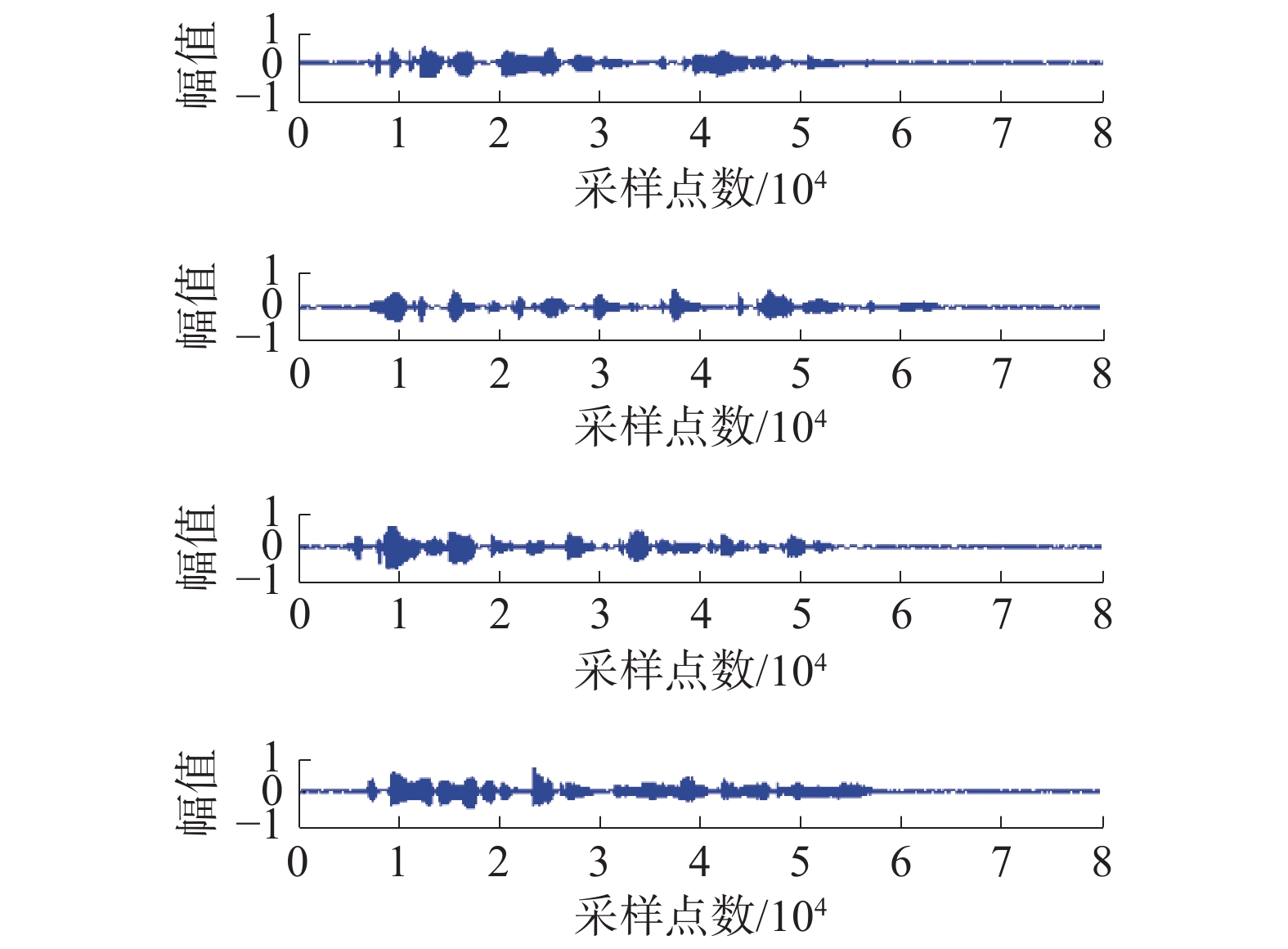
3.1 语音信号的仿真实验实验采用的源信号为随机选取的4段英语听力音频,数据采样点长度为80 000,采样频率为10 kHz,源信号时域波形图如图3所示。
|
Download:
|
| 图 3 语音源信号时域波形 | |
首先,利用混合矩阵模拟声音传播的信道,将4路源信号混合成3路观测信号,本文中混合矩阵A为随机生成的,混合矩阵为
| ${A} = \left[ {\begin{array}{*{20}{c}} {0.750 \; 3}&{ - 0.858 \; 7}&{0.661 \; 9}&{ - 0.262 \; 6} \\ {0.532 \; 7}&{0.175 \; 3}&{0.985 \; 6}&{0.334 \; 3} \\ { - 0.068 \; 7}&{0.464 \; 2}&{0.367 \; 0}&{0.730 \; 9} \end{array}} \right]$ |
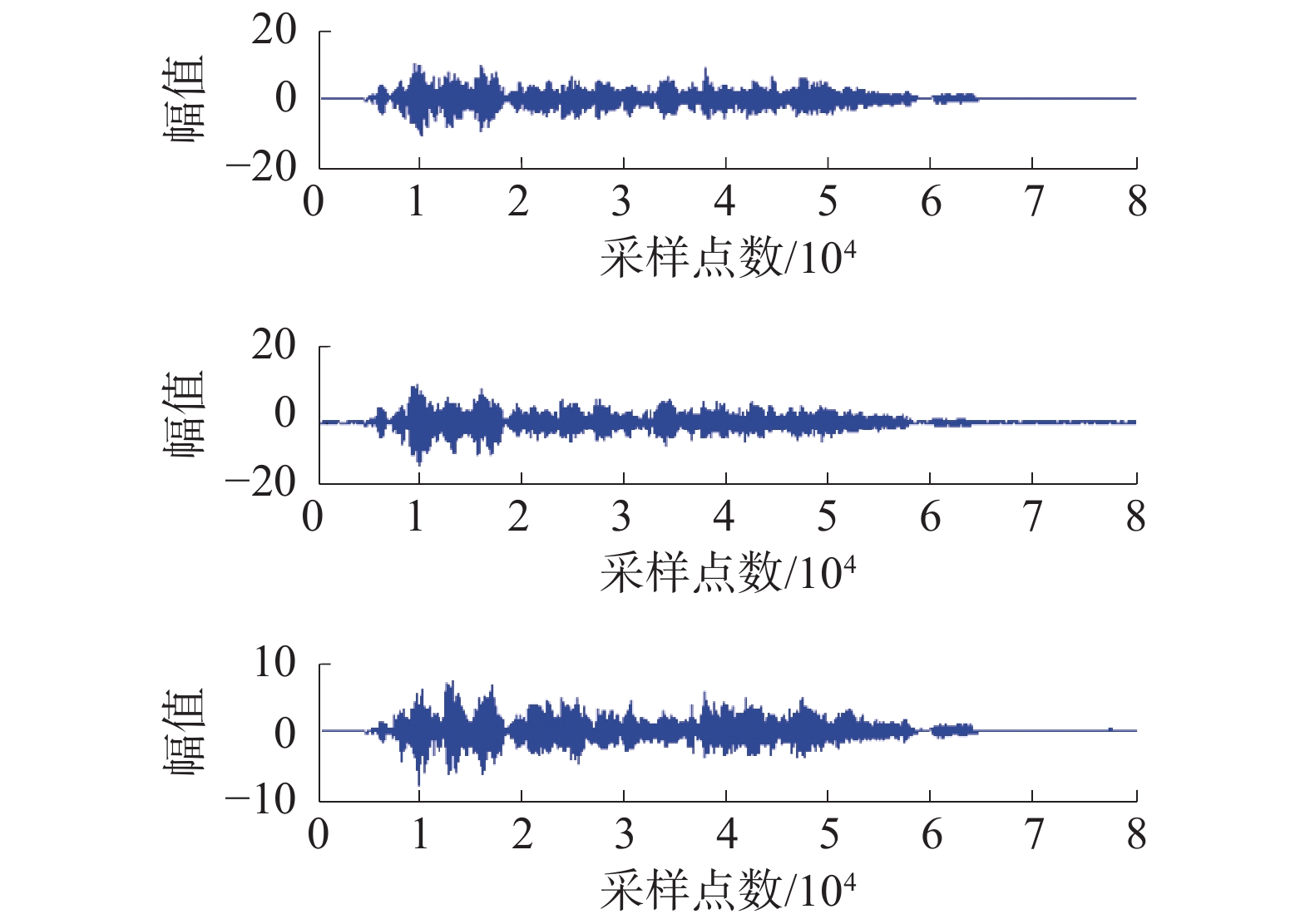
4路源信号经过混合矩阵A传输,形成的观测信号时域波形如图4所示。
|
Download:
|
| 图 4 混合观测信号时域波形 | |
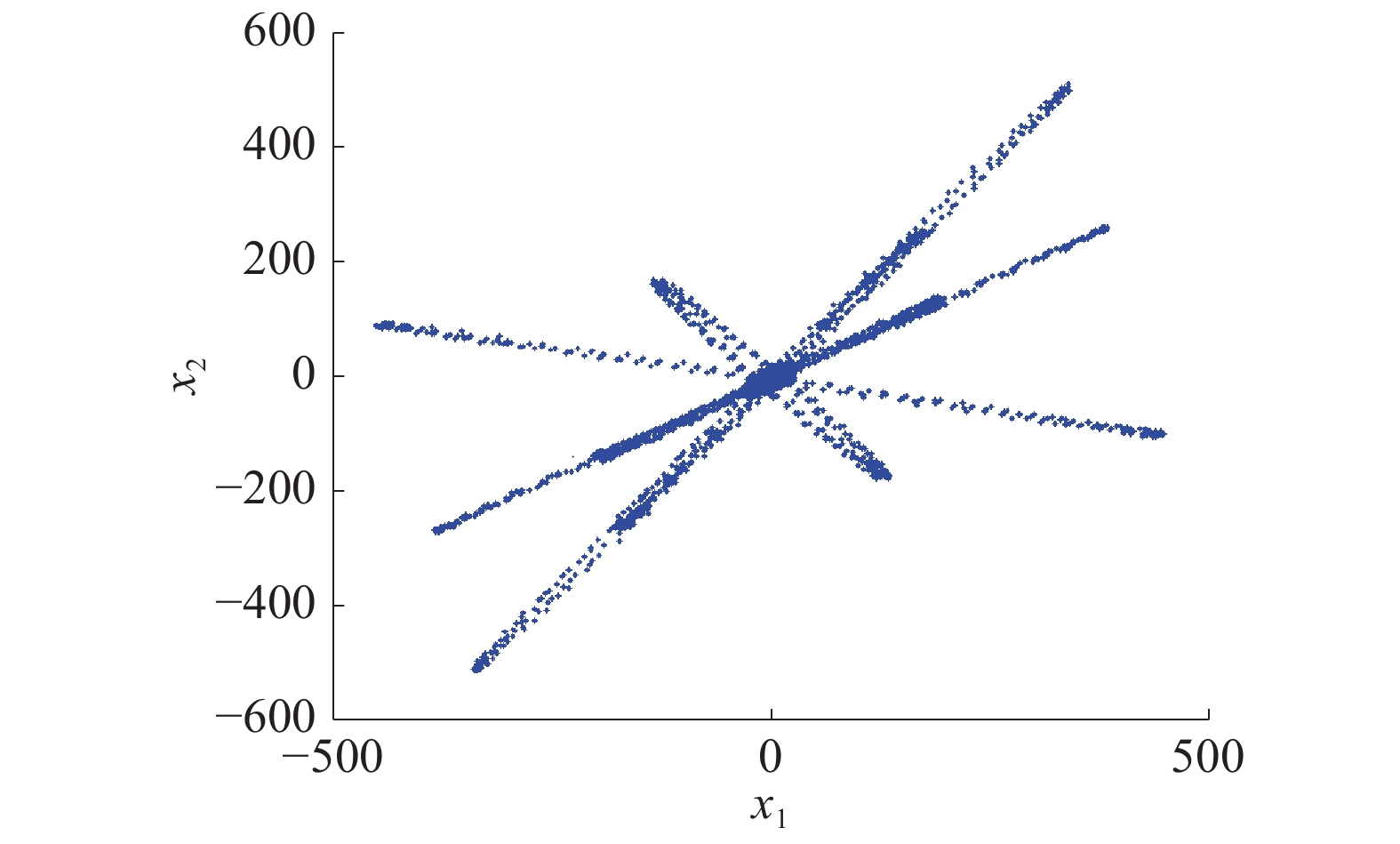
接下来利用时频变换工具,将观测信号进行处理。由于处理语音信号,这里我们选择短时傅里叶变换,使得信号在变换域内尽量稀疏,经过短时傅里叶变换后的散点图如图5所示。
|
Download:
|
| 图 5 未经边缘能量点处理的散点图 | |
经过边缘能量点去除处理后,得到聚类特性增强的散点图,如图6所示。

|
Download:
|
| 图 6 经边缘能量点处理后的散点图 | |
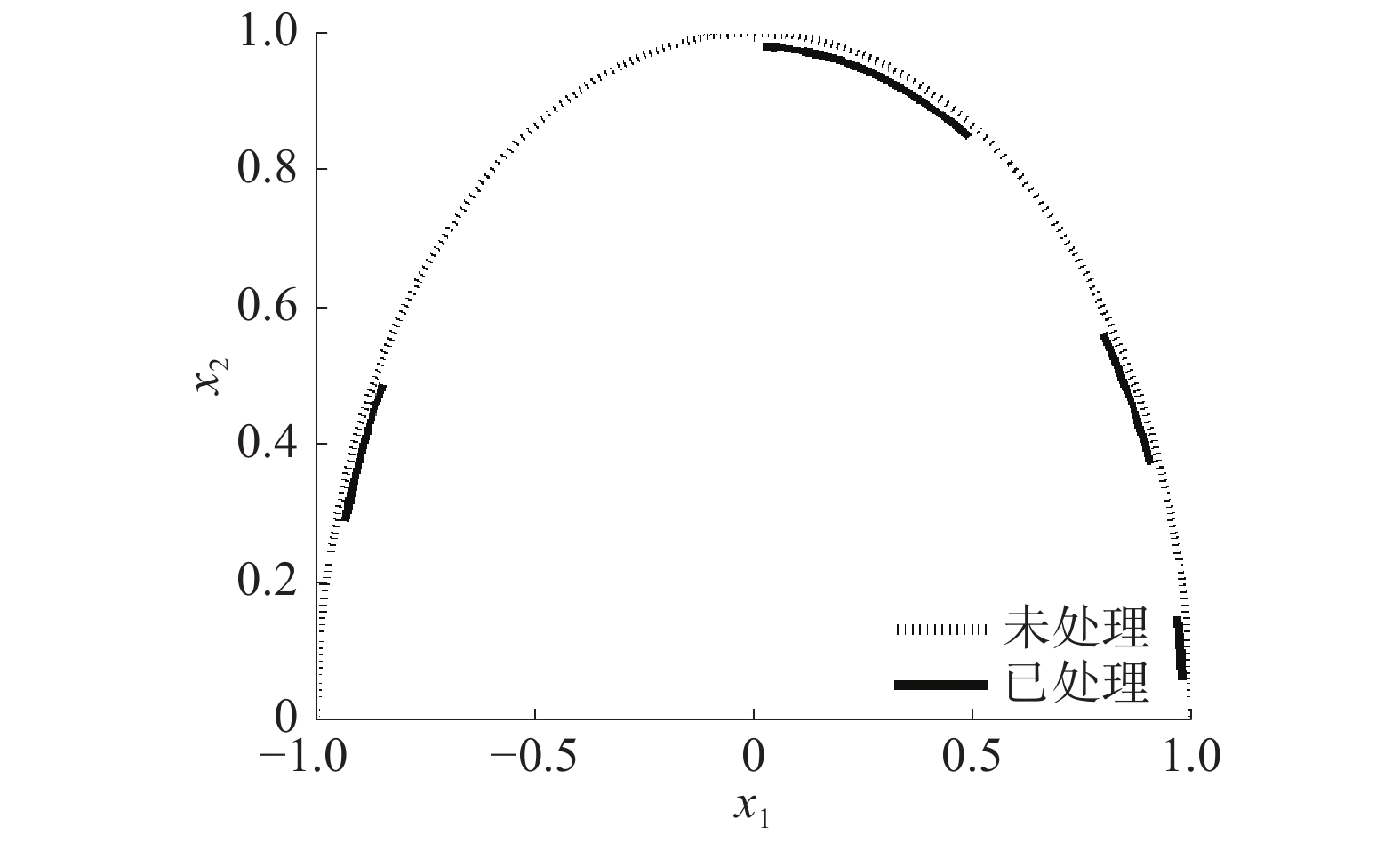
初始化的经边缘能量点处理前后的散点图对比如图7所示。
|
Download:
|
| 图 7 边缘能量点处理前后的初始化散点图对比 | |
最后一步就是估计混合矩阵。首先已确定信源数目为4,则设置初始聚类中心个数为4。信号经过处理后,已呈现出了明显的聚类效果。
利用传统的FCM聚类算法和改进后的FCM聚类算法进行混合矩阵估计。利用传统的FCM聚类算法估计出的混合矩阵为
| ${\hat {{A}}_{{\rm{FCM}}}} = \left[ {\begin{array}{*{20}{c}} {0.707 \; 0}&{ - 0.867 \; 0}&{0.632 \; 1}&{ - 0.245 \; 6} \\ {0.561 \; 9}&{0.178 \; 4}&{0.992 \; 8}&{0.392 \; 8} \\ { - 0.082 \; 2}&{0.466 \; 9}&{0.395 \; 0}&{0.757 \; 9} \end{array}} \right]$ |
经过改进后的FCM聚类算法估计出的混合矩阵为
| ${\hat {{A}}_{{\rm{I - FCM}}}} = \left[ {\begin{array}{*{20}{c}} {0.709 \; 7}&{ - 0.864 \; 5}&{0.652 8}&{ - 0.252 \; 9} \\ {0.568 \; 8}&{0.173 \; 5}&{0.992 \; 3}&{0.386 \; 6} \\ { - 0.073 \; 9}&{0.461 \; 0}&{0.383 \; 5}&{0.753 \; 2} \end{array}} \right]$ |
在最后,将观测信号进行分离实验,得到的结果如图8所示。可以看到源信号能够较好恢复,证明文中采用的改进后的FCM聚类算法是可行的。

|
Download:
|
| 图 8 分离信号波形 | |
评价混合矩阵估计性能的标准有2个[13],分别为
1)归一化均方误差(normalized mean squared error,NMSE)
| ${E_{\rm NMSE}} = 10\lg \left( {\displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{{\left( {{{\hat a}_{ij}} - {a_{ij}}} \right)}^2}} } }}{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{a_{ij}}^2} } }}} \right)$ |
式中:
2)偏离角度
| ${{A}}\left( {{a},\hat {{a}}} \right) = \displaystyle\frac{{180}}{{\rm{\text π}}}\arccos \left( {\displaystyle\frac{{\left\langle {{a},\hat {{a}}} \right\rangle }}{{\left\| {a} \right\| \cdot \left\| {\hat {{a}}} \right\|}}} \right)$ |
式中:
为验证算法性能,将对2种算法从上述2种标准和算法收敛速度方面进行比较。
首先,比较归一化均方误差大小。从表1中数据可以得到,本文改进的算法相比传统的FCM聚类算法,NMSE取值更小,这表示估计出的混合矩阵与原矩阵误差越小,改进后的算法所得的估计矩阵精度高,算法性能更优。
|
|
表 1 归一化均方误差数据对比 |
然后,比较偏离角度大小。表2中数据为估计结果与原混合矩阵对应列向量之间的夹角。可以看到本文改进的算法相比传统的FCM聚类算法,列向量之间偏离角度更小,这也可证明改进后的算法所得的估计矩阵精度高。
|
|
表 2 偏离角度数据对比 |
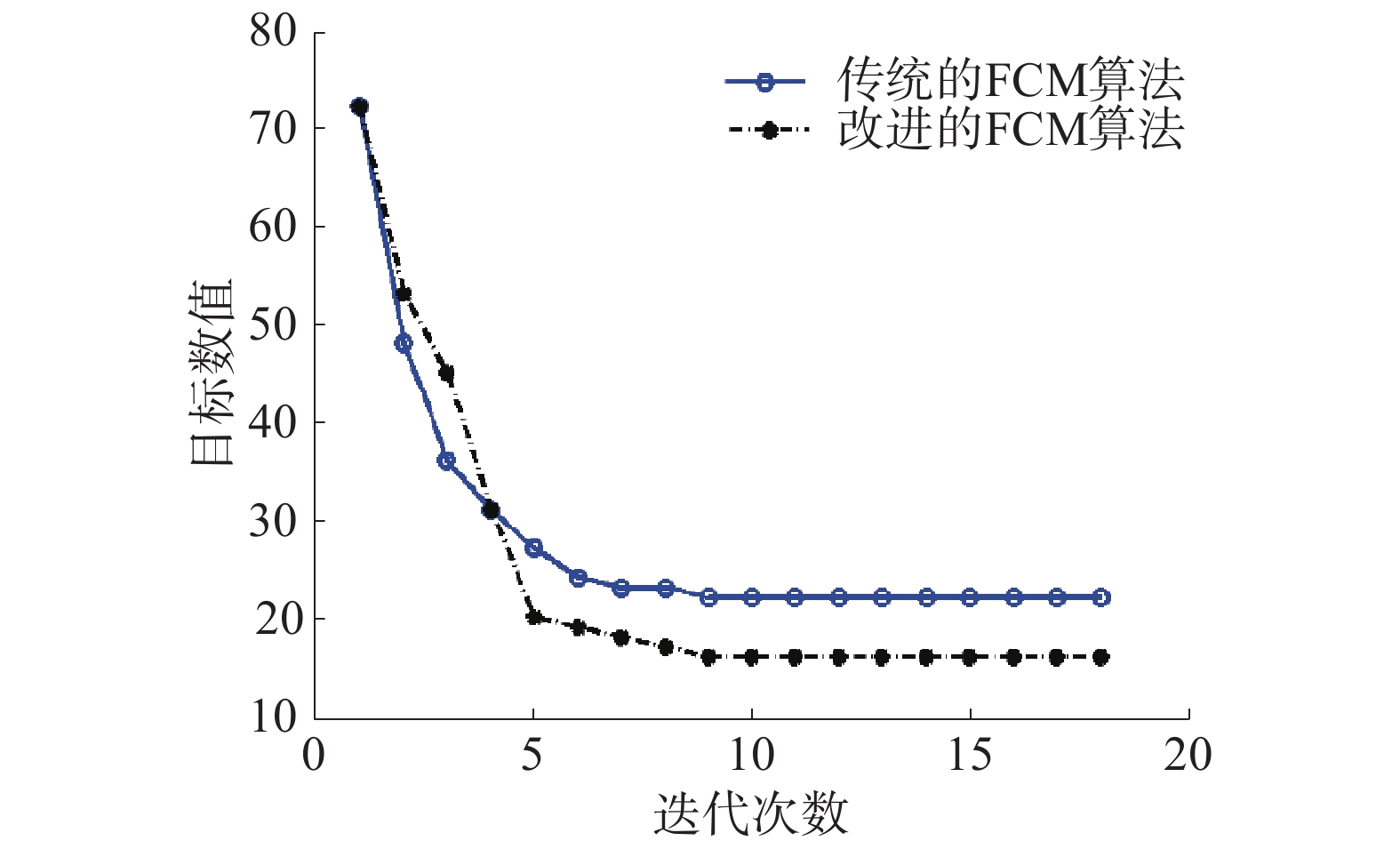
最后,检验算法收敛速度,这需要通过算法中的目标函数收敛情况来判断。如图9所示,本文改进的FCM算法与传统的FCM聚类算法相比,具有更快的迭代速度,这意味着算法的执行效率更高。
|
Download:
|
| 图 9 算法收敛速度对比 | |
基于稀疏分量分析理论,针对FCM聚类算法中隶属度的选取方式的缺陷进行改良,完成语音信号的混合矩阵估计仿真实验。所得结论如下:
1)采用指数形式的修正因子来优化隶属度划分,利用其函数变化速率快的特点,来加快数据点的归类速度,可实现提高算法收敛速度的目的。
2)通过观察实验数据,对比传统的FCM聚类算法和改进后的FCM聚类算法,发现改进后的算法可使得混合矩阵估计精度提高,并且能够提升算法收敛速度。这种较优的性能用在实时性要求更高的环境中就能获得更好的分离效果。
3)并未对算法的稳定性进行验证,这也是后续研究中需要考虑的。而且文中实验涉及的都是纯净的语音信号,在真实的环境中不可避免会受到噪声信号的干扰。所以,进行含噪声环境的实验更具有实际的意义,也需要完成后续的实验。
| [1] |
余先川, 胡丹. 盲源分离理论与应用[M]. 北京: 科学出版社, 2011: 3-9.
( 0) 0)
|
| [2] |
UDDIN Z, AHMAD A, IQBAL M, et al. Applications of independent component analysis in wireless communication systems[J]. Wireless personal communications, 2015, 83(4): 2711-2737. DOI:10.1007/s11277-015-2565-1 ( 0) 0)
|
| [3] |
COREY R M, SINGER A C. Underdetermined methods for multichannel audio enhancement with partial preservation of background sources[C]//2017 IEEE Workshop on Applications of Signal Processing To Audio and Acoustics. New Paltz, USA, 2017: 26-30.
( 0) 0)
|
| [4] |
LI Chengjie, ZHU Lidong, LUO Zhongqiang. Underdetermined blind source separation of adjacent satellite interference based on sparseness[J]. China communications, 2017, 14(4): 140-149. DOI:10.1109/CC.2017.7927572 ( 0) 0)
|
| [5] |
李燕丽, 吴士文, 刘娅, 等. 基于FastICA盲源分离法去除土壤干扰的小麦生物量高光谱估算[J]. 生态学杂志, 2017, 36(4): 1158-1164. ( 0) 0)
|
| [6] |
BOBIN J, RAPIN J, LARUE A, et al. Sparsity and adaptivity for the blind separation of partially correlated sources[J]. IEEE transactions on signal processing, 2015, 63(5): 1199-1213. DOI:10.1109/TSP.2015.2391071 ( 0) 0)
|
| [7] |
黄文威, 凌云, 徐敬成. 基于FCM聚类和蚁群优化的WSN路由算法[J]. 信息与电脑(理论版), 2018(1): 38-40. ( 0) 0)
|
| [8] |
张红丽. 基于稀疏性增强的欠定盲源分离算法研究[D]. 秦皇岛: 燕山大学, 2016: 30.
( 0) 0)
|
| [9] |
DE LATHAUWER L, CASTAING J. Blind identification of underdetermined mixtures by simultaneous matrix diagonalization[J]. IEEE transactions on signal processing, 2008, 56(3): 1096-1105. DOI:10.1109/TSP.2007.908929 ( 0) 0)
|
| [10] |
朱然, 李积英. 几种优化FCM算法聚类中心的方法对比及仿真[J]. 计算机技术与发展, 2015, 25(5): 17-20. ( 0) 0)
|
| [11] |
刘锐, 张宁. 一种动态加权模糊聚类算法的研究[J]. 铁路计算机应用, 2018, 27(5): 5-8, 17. DOI:10.3969/j.issn.1005-8451.2018.05.002 ( 0) 0)
|
| [12] |
武玉坤. 融合特征值与优化划分的改进FCM聚类算法[J]. 计算机工程与设计, 2017, 38(4): 1076-1080. ( 0) 0)
|
| [13] |
CHEN Peng, PENG Dezhong, ZHEN Liangli, et al. Underdetermined Blind Separation by Combining Sparsity and Independence of Sources[J]. IEEE access, 2017, 5: 21731-21742. DOI:10.1109/ACCESS.2017.2764044 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


