全球卫星导航系统在人们生产生活中使用的越来越广泛，军事上对其也是愈发依赖。导航信号到达地面时功率较低且系统信号体制公开，容易受到各式各样的人为干扰。欺骗干扰是一种典型的人为干扰，与压制干扰作用机理不同，欺骗干扰通过发射虚假导航信号，依靠功率优势诱导接收机对其进行捕获跟踪，解算出错误的定位结果^[1−3]。欺骗干扰由于应用灵活广泛且威胁性较强，已成为威肋卫星导航安全的重要因素，严重影响着全球卫星导航系统的定位与授时服务质量。因此，对卫星导航系统的抗欺骗干扰研究意义重大。

欺骗检测技术是抗欺骗技术研究的第一步，也是非常关键的一步。针对欺骗干扰的检测国内外学者也提出了一些方法，如Psiakiti^[4]提出了一种利用2台不同系统的接收机进行欺骗式干扰检测的方法，Nielsen提出了一种利用手持单天线接收机对欺骗式干扰进行检测的方法，黄龙^[5~6]在多篇论文中也对欺骗干扰的检测方法进行了总结和分析。本文针对跟踪阶段欺骗式干扰的检测需求，采用基于信号功率异常检测和多普勒频移检测的欺骗干扰检测算法实现对欺骗干扰的检测，并通过仿真验证了算法的性能。

1 跟踪阶段系统模型分析

当欺骗者对接收机进行欺骗时，接收机接收到的信号就会是欺骗干扰信号和真实信号叠加后的复合信号。而由于北斗信号采用的是码分多址原理，在复合信号与本地伪随机码相关解扩后，接收机分通道处理不同卫星信号，进行跟踪、电文解调和导航解算。只有与导航卫星测距码号相同的欺骗干扰能对其真实信号产生影响，接收机的跟踪通道中实际处理的也是该颗卫星的真实信号与该颗卫星欺骗信号叠加的复合信号。

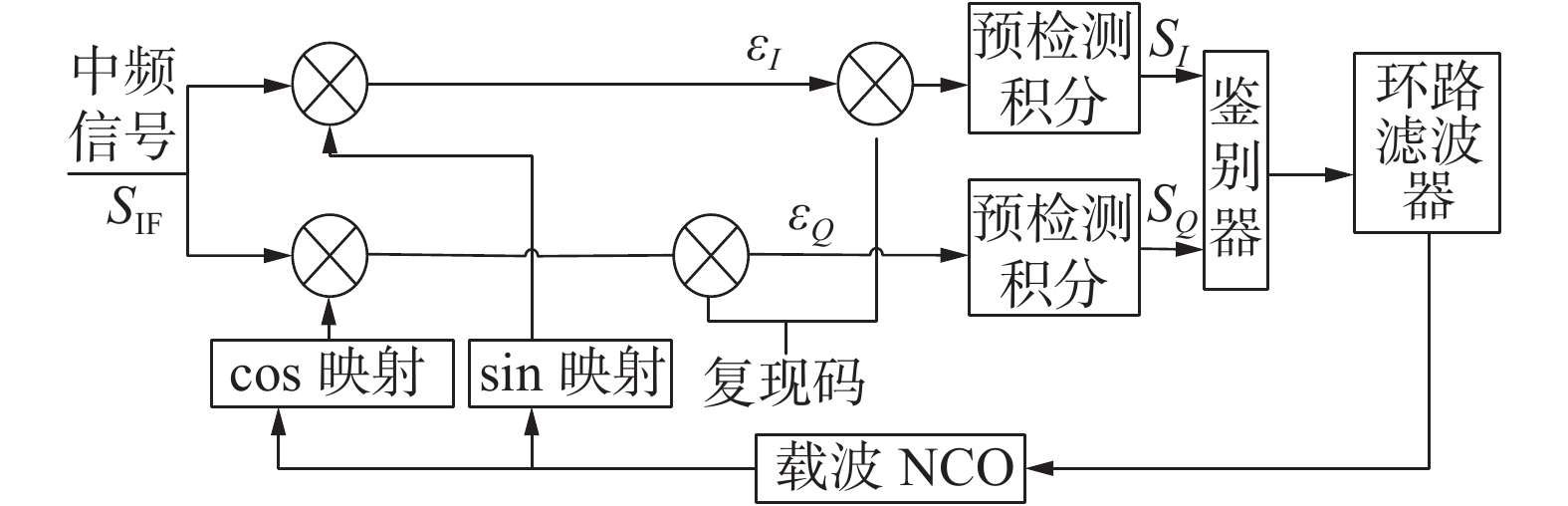
1.1 正常接收信号模型

在信号跟踪阶段^[7]，首先接收机射频阶段处理后的数字中频信号进入到跟踪环路中，载波振荡器产生载波后，经过处理产生相应的正弦复制载波和余弦复制载波；然后与数字中频信号相乘并下变频，将得到的2路信号进行一定时长的预检测积分（通常为1 ms或者其整数倍）；最后鉴相并通过环路滤波器得到载波振荡器产生载波的误差信号，以此调整载波。以上步骤迭代处理，确保接收机稳定的跟踪信号。图1为接收机锁相环结构示意图^[8]。

跟踪环路的中频信号为：

${S_{{\rm{IF}}}}(t) = A(t)C(t)D(t)\sin ({\omega _{{\rm{IF}}}}t + {\theta _{{\rm{IF}}}}) + {n_{{\rm{IF}}}}$

式中：A表示接收信号的信号幅度； $C$ 表示接收信号的伪随机码；D表示接收信号的数据； ${\omega _{{\rm{IF}}}}$ 为中频频率； ${\theta _{{\rm{IF}}}}$ 为载波相位； ${n_{{\rm{IF}}}}$ 为均值为0、方差为 $\sigma _{}^2$ 的高斯白噪声。

当本地码与伪随机码完全对齐时，解扩后的中频信号为

${S_{{\rm{IF}}}}(t) = A(t)D(t){\rm{sin}}({\omega _{{\rm{IF}}}}t + {\theta _{{\rm{IF}}}}) + {n_{{\rm{IF}}}}$

本地产生的2路正交的载波信号可表示为

${S_{{L_I}}}(t) = {\rm{sin}}({\omega _L}t + {\theta _L}){\kern 1pt} {\kern 1pt} {\kern 1pt} $

${S_{{L_Q}}}(t) = \cos ({\omega _L}t + {\theta _L}){\kern 1pt} {\kern 1pt} $

将解扩后的中频信号与本地载波信号相乘，得到混频信号 ${\varepsilon _I}$ 和 ${\varepsilon _Q}$ ：

$ \begin{aligned} \;\; {\varepsilon _I} = & A(t)D(t)\frac{{\cos \; {\varphi _1} - \cos {\varphi _2}}}{2} + {n_c}(t)\frac{{\sin \;{\varphi _1} + \sin \;{\varphi _2}}}{2} + \\ \;\; & {n_s}(t)\frac{{\cos \; {\varphi _1} - \cos \; {\varphi _2}}}{2} \end{aligned} $

$ \begin{aligned} \;\;\;\; {\varepsilon _Q} = & A(t)D(t)\frac{{\sin \; {\varphi _1} - \sin \; {\varphi _2}}}{2} + {n_c}(t)\frac{{\cos \; {\varphi _1} + \cos \; {\varphi _2}}}{2} + \\ \;\;\;\; & {n_s}(t)\frac{{\sin \; {\varphi _1} - \sin \; {\varphi _2}}}{2} \end{aligned} $

对 ${\varepsilon _I}$ 和 ${\varepsilon _Q}$ 进行积分，积分时间的长度设置为 $T$ ，假设在积分时间内幅度和数据均不变，则积分后的信号为

${S_I}(t) = \frac{{ADT\cos \;{\varphi _1}}}{2} + \frac{{{N_c}\sin \; {\varphi _1}}}{2} + \frac{{{N_s}\cos \; {\varphi _1}}}{2}$

${S_Q}(t) = \frac{{ADT\sin \;{\varphi _1}}}{2} + \frac{{{N_c}\cos \; {\varphi _1}}}{2} + \frac{{{N_s}\sin \; {\varphi _1}}}{2}$

式中 ${N_c}$ 与 ${N_s}$ 均服从均值为0、方差为 $\sigma _{}^2T/2$ 的高斯分布。

当接收信号为真实信号、不存在欺骗干扰信号锁相环能稳定跟踪的情况下，鉴相误差 ${\varphi _1}$ 接近于0。此时， $Q$ 支路输出的是噪声，I支路输出的是数据和噪声。

1.2 欺骗信号入侵后的接收信号模型

当接收到的信号不仅具有真实信号，同时还混有欺骗信号时，其模型与正常接收信号模型存在一定差别。

欺骗信号可以表示为^[9]：

${S_S}(t) = {A_S}(t){C_S}(t){D_S}(t){\rm sin}({\omega _S}t + {\theta _S})$

式中： ${A_S}$ 为欺骗信号幅度； ${C_S}$ 为欺骗信号伪随机码； ${D_S}$ 为欺骗信号数据； ${\omega _S}$ 为欺骗信号中频频率； ${\theta _S}$ 为欺骗信号载波相位。

此时接收机的输入信号为：

$S(t) = {S_{{\rm{IF}}}}(t) + {S_S}(t)$

若2个信号的码相位完全对齐，则：

$S(t) = C(t)D(t){A_M}(t){\rm cos}({\omega _{IF}}t + {\theta _M}) + n(t)$

式中： ${A_M}(t)$ 为合成信号幅度； ${\theta _M}$ 为合成信号相位； ${w_{{\rm{IF}}}}$ 为复合信号的中频频率。由此可见接收机接收到的复合信号在信号幅度和信号频率上较正常信号有所区别。

2 跟踪阶段欺骗检测方法设计

在欺骗式干扰信号加入后，会造成跟踪环路中载波信号幅度发生变化^[10]，多普勒频移会有变化。依据以上原理，本文将功率异常检测、多普勒频移检测2种方法结合使用，在跟踪阶段检测接收机信号中是否存在欺骗式干扰信号。

2.1 信号功率异常检测算法设计

信号功率异常检测算法是利用接收信号的载噪比，与记录的载噪比历史数据进行比较完成检测过程^[11]。通过研究发现，计算特定窗口大小下的载噪比的移动方差来监测载噪比的变化情况是有效的检测手段。

通过计算数据集的方差并将其向前移动，创建一个新的数据子集，从而计算出一个新的方差，以获得移动方差。这个过程在整个数据系列中重复进行。由计算得到的方差组成的新的数据集代表移动方差。表示移动方差的公式如下：

$ \begin{aligned} \sigma _{MV}^2 =& \frac{1}{W}\sum\nolimits_{k = n - W + 1}^n {{{[x(k) - \overline {x(n)} ]}^2}} - \overline {x(n)} = \\ & \overline {{x^2}(n)} - \overline {x(n)} \end{aligned} $

式中： $\overline {x(n)} $ 是子集 $W$ 中样本的平均值， $\overline {{x^2}(n)} $ 是在子集 $W$ 中样本的平方和，而 $n$ 是样本容量， $W$ 是窗口大小。在窗口大小取10，积分时间为400 ms时，通过移动方差可以很容易地检测出欺骗式干扰信号。如图2所示，图中记录了3个卫星的载噪比移动方差变化情况，其中有2个真实卫星数据和1个使用模拟器模拟的转发式欺骗干扰信号，可以很容易地检测出有欺骗干扰信号存在。

2.2 多普勒频移异常检测算法设计

跟踪阶段的第二个欺骗检测方法是基于接收到的北斗信号的多普勒频移量的历史数据^[12]。北斗B1I信号的载波频率为1 561.098 MHz，由于卫星与北斗接收机的相对运动，产生了多普勒频移。卫星的速度可以通过接收机接收到的卫星星历数据获得。接收到的载波频率，随着卫星接近接收机而变大，卫星远离接收机而变小，它可以近似于经典的多普勒方程：

${f_r} = {f_c}(1 - \frac{{a{v_r}}}{c})$

式中： ${f_c}$ 是卫星发射的标准载波频率； ${f_r}$ 是接收到的载波频率； ${v_r}$ 是卫星和接收机之间的相对速度矢量； $c$ 是光速； $a{v_r}$ 是相对速度矢量的径向分量。在卫星和接收机的相对运动中，静态接收机的多普勒频移频率的最大值大约是每分钟40 Hz，可以将其多普勒频移看作是线性的。而如果北斗接收机是运动的，那么可以通过接收机的速度和高度来估算多普勒频移的变化。

跟踪多普勒频移量可以在欺骗者试图让北斗接收机锁定到欺骗信号时，检测出接收机开始遭遇到欺骗攻击。如果在跟踪过程中执行了多普勒频移量检测，那么在导航信息被解码之前，可以检测到欺骗信号并消除欺骗干扰。对于静态的北斗接收机，如果接收机的时钟是稳定的，则可以假定多普勒频移量是线性变化的，并基于线性变化的标准下根据历史数据定义的多普勒频移量，设定出多普勒频移量变化的阈值。如果接收机接收到的多普勒频移量超出了事先设定的统计计算阈值，那么北斗接收机就可以将接收到的信号视为欺骗式干扰信号。而且，在北斗接收机失锁的情况下，接收机也可以通过线性预测模型估计多普勒频移量。一旦北斗信号重新锁定，估计的多普勒频移量可以与接收到的频移量进行比较，以确定是否为欺骗信号。

多普勒频移的平滑变化，同时能够在长时间内以低的、几乎不变的误差来预测，使得可以基于多普勒频移变化来实现检测欺骗干扰。

图3显示了跟踪来自采集器采集的无干扰情况下的北斗中频信号的多普勒频移变化情况，多普勒频移的最大变化速率在20 Hz左右，变化趋势呈现线性变化。这表明只要有足够多的样本数据，就可以估计多普勒频移量。

根据上述情况，在一个特定大小的窗口中，多普勒频移的移动方差可以用来显著地检测多普勒频移量的变化情况。图4显示了样本窗口大小为100、500和1 000时多普勒频移的移动方差。图4显示当窗口大小大于100后，多普勒频移的移动方差不会超过35 Hz。统计分析显示，即使有较小的窗口，例如窗口大小为10时，并且考虑所有的卫星，90%的情况下多普勒频移量也不会超过40 Hz。因此，将多普勒频移移动方差的阈值设置为40 Hz，可以提供一个可靠的检测，用来检测欺骗攻击。此外，一旦触发了基于多普勒频移移动方差阈值检测的欺骗干扰攻击警报，基于线性预测模型的多普勒频移预测可以为北斗接收机提供近似多普勒频移量来继续跟踪真实信号。

3 仿真实验

为了验证提出欺骗保护算法的有效性，利用MATLAB仿真，通过实验进行验证。不考虑被欺骗接收机位置的简单欺骗式干扰攻击，是很容易被接收机检测到的；而能在攻击下获得被干扰接收机的实时位置的欺骗干扰攻击信号，是很难被检测到的。在本章的仿真实验中，我们定义2种不同类型的干扰。

类型一欺骗干扰：产生式欺骗干扰，模拟真实信号，产生伪造的导航信号，欺骗接收机。

类型二欺骗干扰：转发式欺骗干扰，采用“接收信号—转发信号”模式，解算接收到的真实卫星信号，在真实卫星信号的基础上，对信号进行简单修改，欺骗接收机。

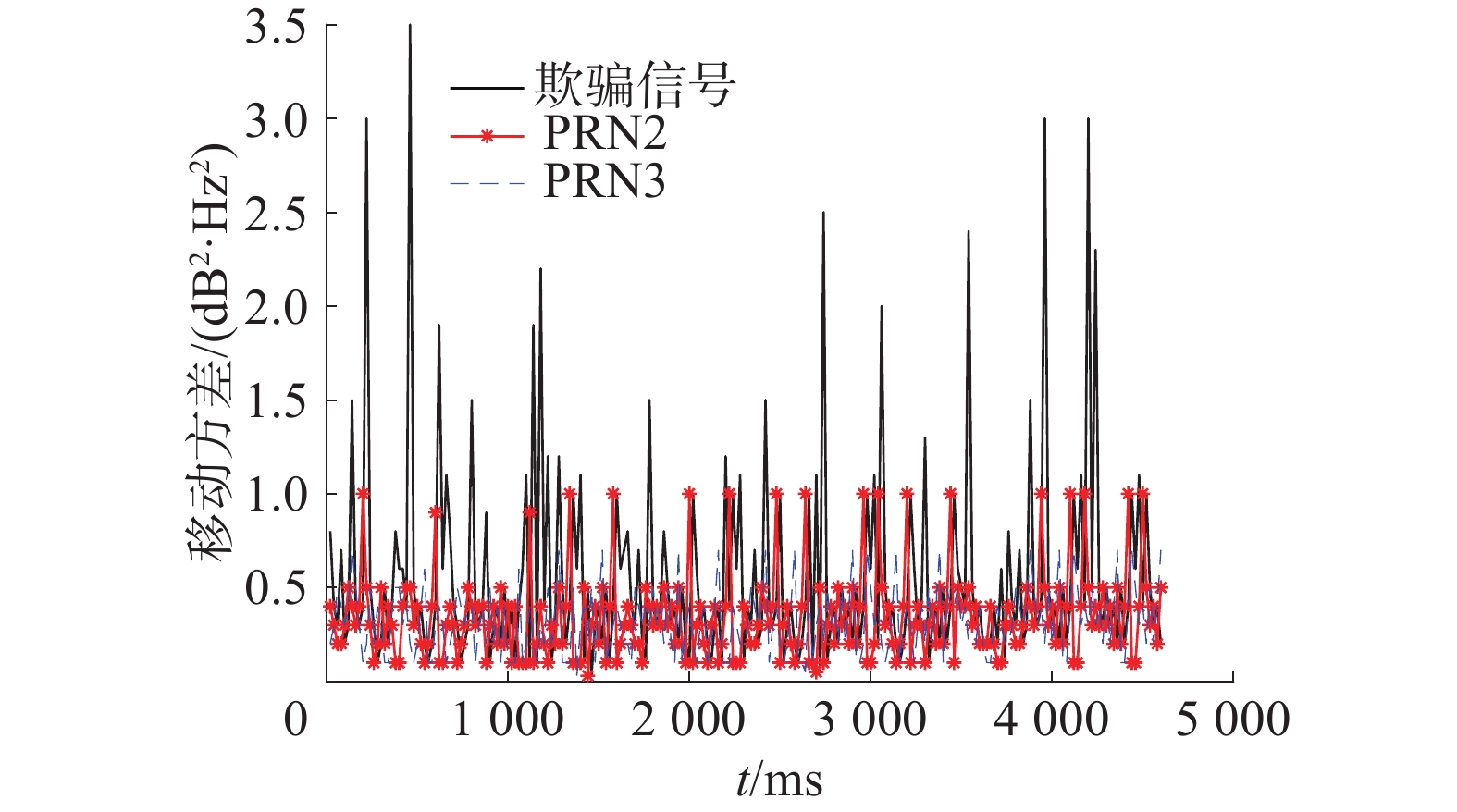
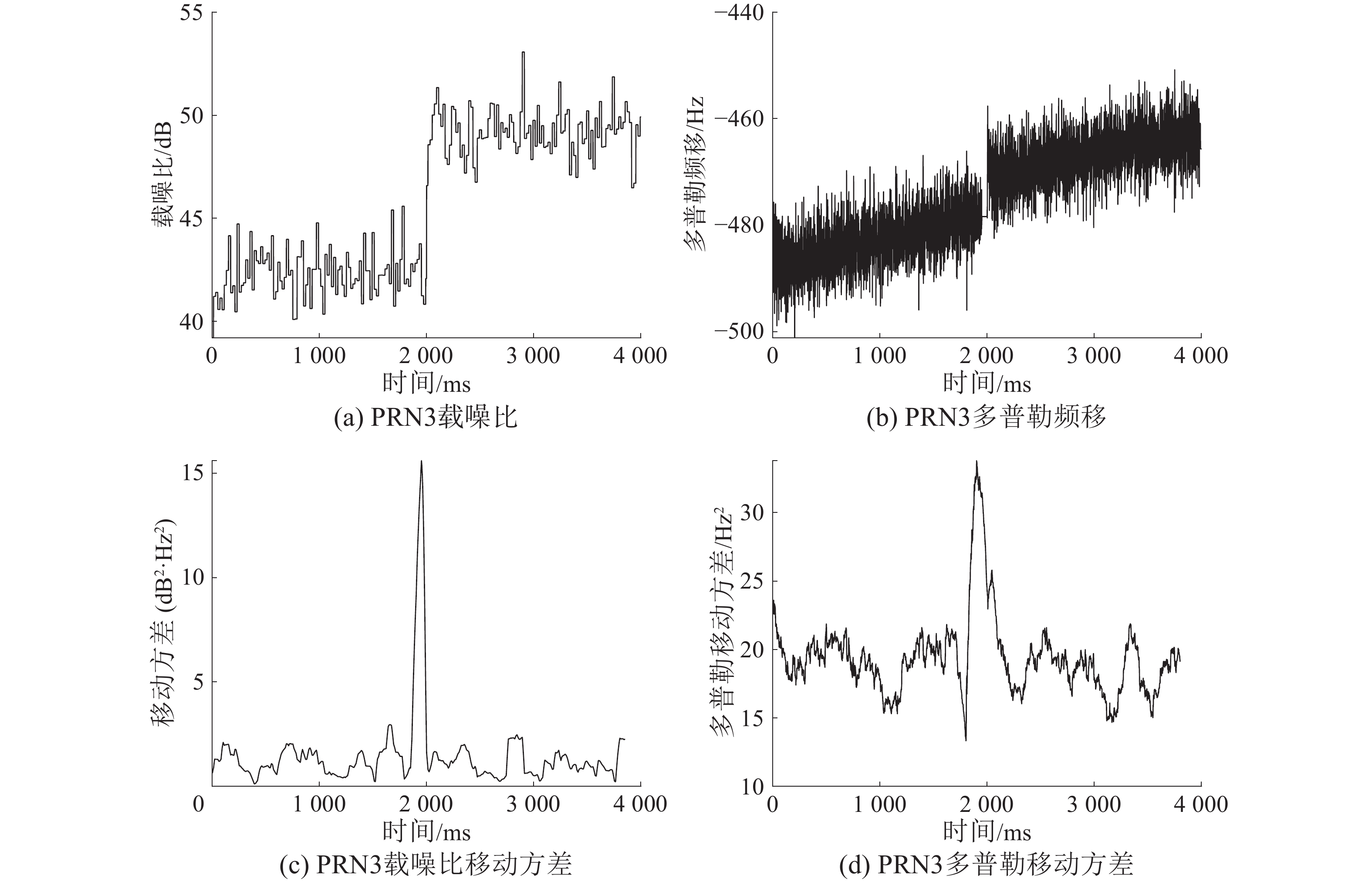
北斗PRN3卫星信号的类型一欺骗干扰的功率异常检测和多普勒频移检测仿真结果如图5所示。很明显，通过执行信号功率异常检测和多普勒频移检测，可以检测到在跟踪卫星信号的第2 s左右，检测到跟踪信号中存在欺骗式干扰信号。图5中载噪比移动方差在第2 s左右有一个幅度为4的峰值，而多普勒频移的移动方差图中在第2 s左右有一个幅度大于500的峰值。可以看出多普勒频移检测的结果很明显，接收到的多普勒信号有50 Hz以上的明显频移，而信号功率异常检测的结果并不明显，这是因为仿真所用欺骗信号与真实信号的功率是相似的，但是多普勒频移的差异很大。如图6所示，在另一个类型一欺骗干扰例子中，欺骗信号试图与真实北斗信号的多普勒频移进行匹配，但是信号功率检测有明显的变化，这很容易被功率异常检测算法检测到。以上仿真说明基于信号功率异常检测和多普勒频移检测分别设置阈值，可以成功地检测到类型一欺骗干扰，即简单欺骗干扰。

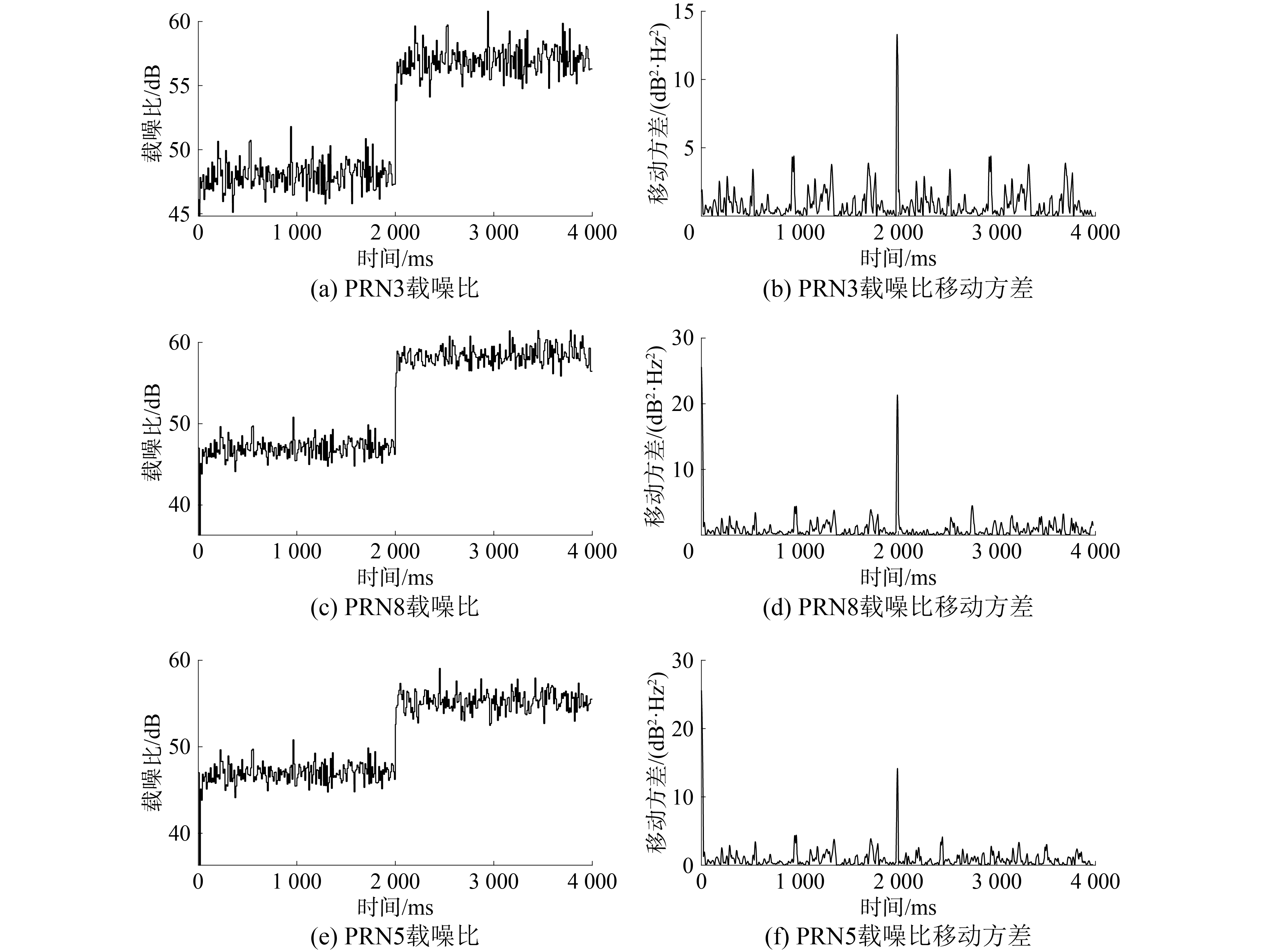
类型二欺骗干扰的功率异常检测和多普勒频移检测仿真结果如图7、8所示。在本次仿真中，我们同时模拟3颗卫星在同一时间受到转发欺骗式干扰信号的影响。图7、8分别表示的是测距码编号为3号、8号、5号的3颗卫星的功率异常检测和多普勒频移检测仿真图。由图7可以发现，在第2 s时间左右，信号的载噪比有明显升高，且载噪比的移动方差中出现了一个明显的峰值。由图8可以发现，当欺骗式信号干扰接收机时，多普勒频移量稍有变化，多普勒频移量移动方差中会有明显的超过设定阈值的表现。图7、8的仿真图可以充分表明信号功率异常检测和多普勒频移检测对于类型二欺骗干扰检测效果明显。

通过仿真实验，可以发现信号功率异常检测和多普勒频移检测可以非常有效地检测出欺骗干扰。

多普勒频移检测的概率密度函数服从对数正态分布，因此，它的概率密度函数和积累分布函数可以表示为：

${p_{\rm df}}(x) = \frac{1}{{x\sigma \sqrt {2{\rm{{\text{π} }}}} }}\exp ( - \left( {\log (x) - \mu } \right)/2{\sigma ^2})$

$c_{\rm df}(x) = \frac{1}{2} + \frac{1}{2}{\rm erf}\left[ {\frac{{\ln (x) - \mu }}{{\sqrt {2{\sigma ^2}} }}} \right]$

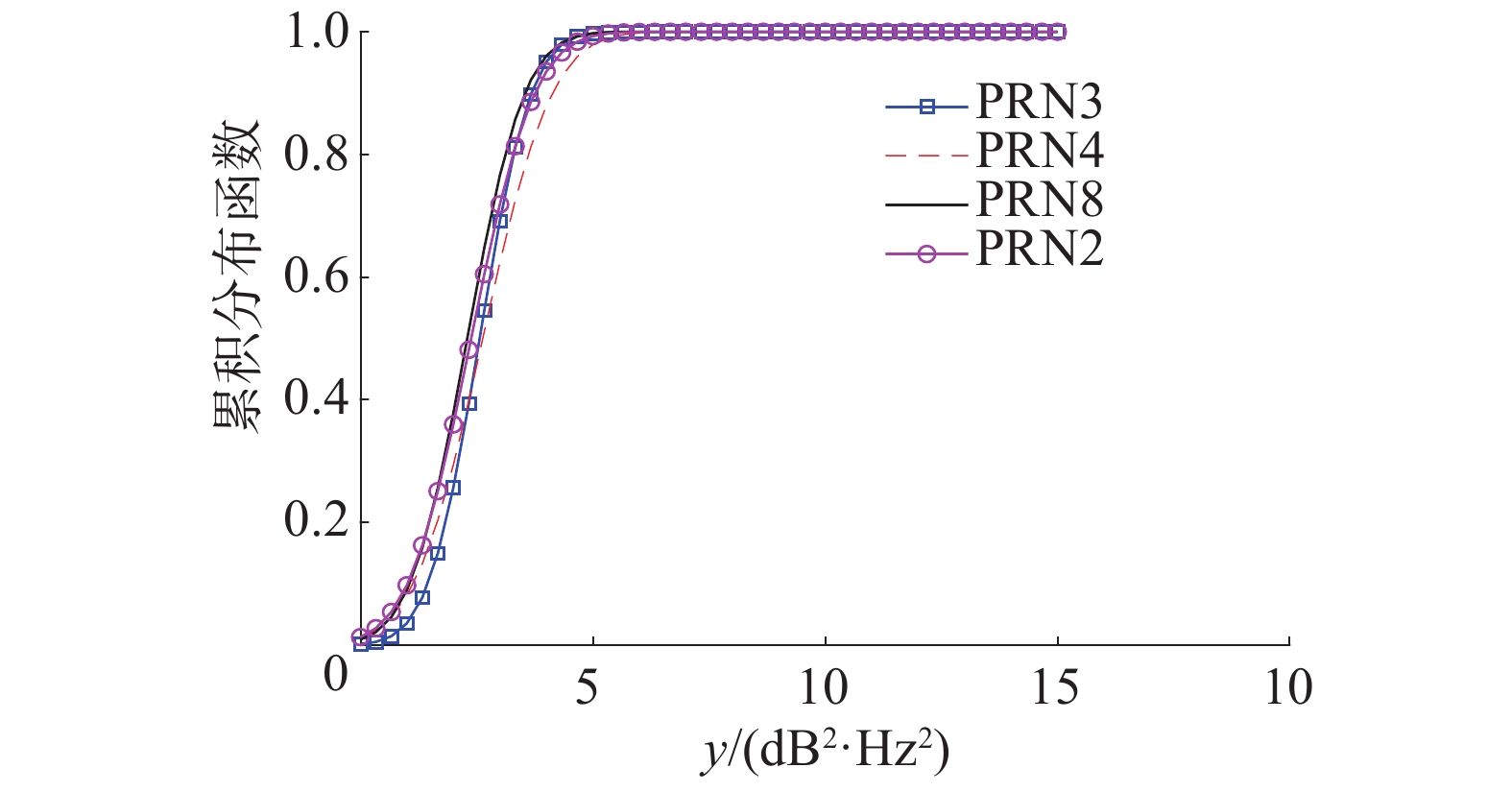
图9、10为不同卫星的多普勒频移移动方差的概率密度函数和累积分布函数。由图10可知，检测概率高于99%时，多普勒频移量的移动方差阈值可以设置为80 ${\rm{H}}{{\rm{z}}^{\rm{2}}}$ ，在这个阈值情况下，虚警概率 $P_{{\rm{fa}}}^{{\rm{DOD}}}$ 为 $1.682 \times {10^{ - 4}}$ 。

根据实验数据，使用MATLAB程序对功率异常检测算法的载噪比移动方差进行1 000次模特卡洛仿真，得到载噪比移动方差的概率密度函数和积累分布函数如图11、12所示，可以从图中看出载噪比移动方差也是服从对数正态分布的。与多普勒频移检测类似，功率异常检测的载噪比移动方差阈值为10，在这个情况下，虚警概率 $P_{{\rm{fa}}}^{{\rm{PTD}}}$ 为 $1.499 \times {10^{ - 4}}$ 。

可以计算出跟踪阶段检测方法的总体虚警概率 ${P_{{\rm{fa}}}}$ ，总的虚警概率为

${P_{\rm fa}} = P_{\rm fa}^{\rm PTD} \cdot P_{\rm fa}^{\rm DOD} = 2.271\;3 \times {10^{ - 8}}$

由此可以说明，跟踪阶段欺骗检测的总体虚警概率非常小，这意味着使用跟踪阶段欺骗检测算法的欺骗检测概率非常高。

4 结束语

本文以实际应用为背景，主要研究了北斗信号跟踪阶段欺骗式干扰检测算法，通过对跟踪阶段北斗导航信号系统模型的分析，提出了基于信号功率异常检测的欺骗干扰检测算法和基于多普勒频移检测的欺骗干扰检测算法。分别对2种算法需要检测变量的历史数据进行分析，验证了算法的可行性，并且在单独分析2种算法的基础上，实现了跟踪阶段欺骗式干扰检测算法。在理论上分析了欺骗攻击的检测概率和虚警概率的关系，并仿真验证所提算法的有效性。