随着我国经济的高速发展，超高压、超长距离输电线路越来越多，成为我国居民作业、生活不可或缺的一部分。因此，维护输电线路的良好运作是居民安全用电的重要保障。由于架空输电线长期暴露在外，易因持续的机械张力、雷击闪络、材料老化或其他人为因素的影响而产生倒塔、断股、磨损、腐蚀、受力等损伤。因此，电力公司需要对输电线路进行定期巡视检查，随时了解和掌握输电线路的运行情况以及线路周围环境和线路保护区的变化情况，以便及时发现、预防事故的发生，确保供电安全。传统的人工巡检方法时间长、成本高、困难大、风险高^[1]，不适用于长距离、大跨度的架空输电线路巡检。近年来，电力行业普遍使用无人机代替人工进行输电线路巡检^[2]，但是随着电网规模的不断扩大，仅利用无人机拍摄输电线路影像，并通过人工查看检验的半人工化方式已不满足我国电力发展需求。其中，基于航拍图像的电力线提取是无人机智能化巡检的关键步骤。电力线的准确定位和提取是电力线交叉跨越距离测量的基础，也是实现无人机自动跟踪输电线路的重要技术依据。

航拍图像背景复杂，涵盖了道路、河流、湖泊、房屋等很多的干扰信息^[3]，如何从复杂背景中准确、完整地提取电力线是研究中的重点和难点。文献[3]提出的利用Canny算子和Hough变换提取电力线的方法，仅考虑了电力线的直线形态，忽略了电力线的悬链线形态检测需求^[4]。文献[5]提出一种基于ratio边缘检测算子和Ransac算法的电力线自动提取算法，但该算法在利用电力线像素点拟合二次电力曲线的过程中，舍弃了一组内多个分裂导线，只用一条导线代替多个分裂导线^[5]，造成提取的电力线数量不完整，准确度低。针对现有算法中存在的问题，本文提出了一种电力线分割算法，利用Gioi等提出的局部直线段检测（LSD）算法和统计学特征提取图像中的电力线。实验结果表明，本文算法能在多种场景下准确完成直线与悬链线2种形态输电线的提取，稳定性好。

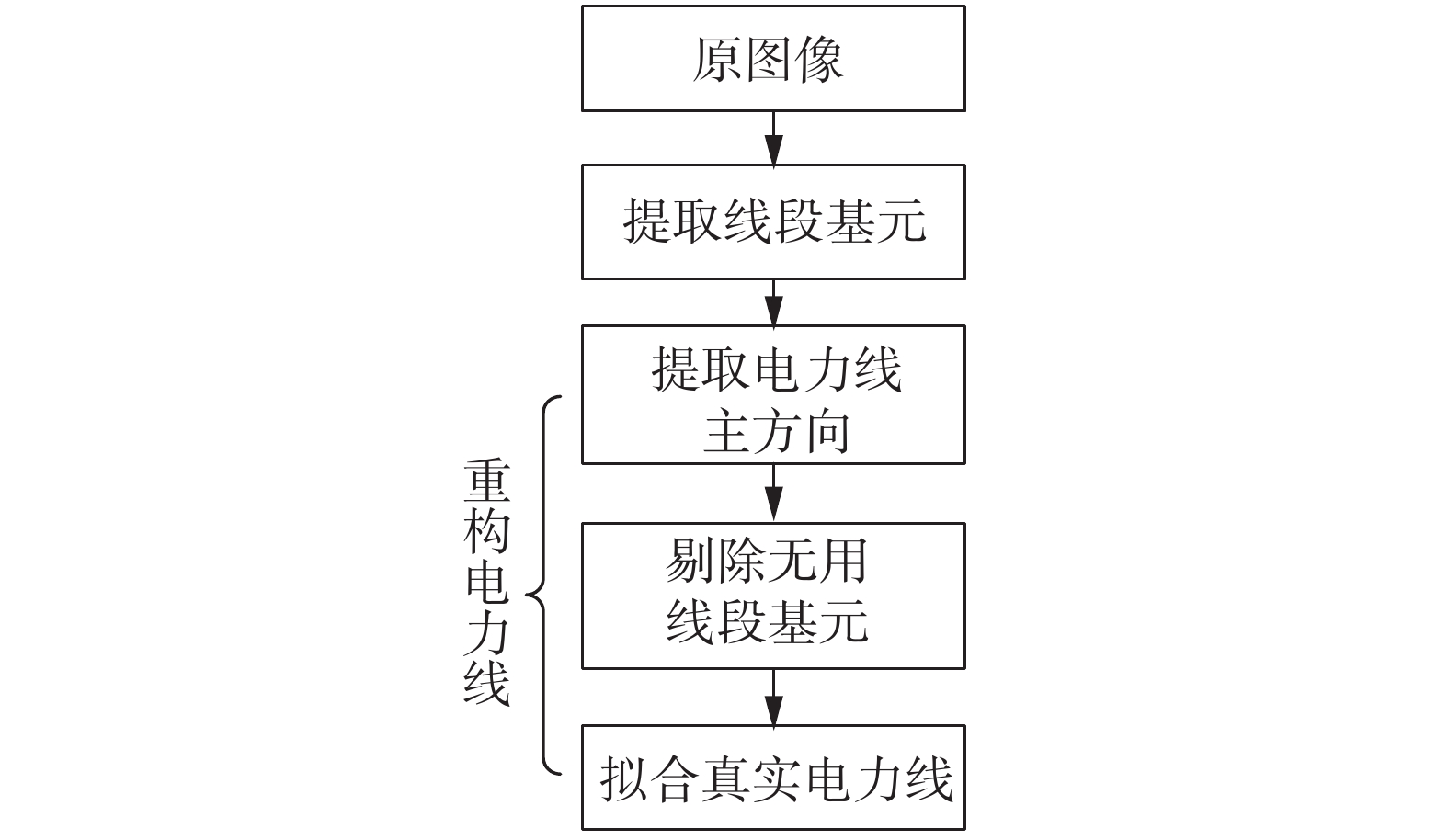
1 电力线检测方法 1.1 算法流程

本文提出的电力线提取算法流程，分为局部线段基元提取和中层视觉感知聚集2个步骤。在局部处理阶段，先做边缘检测，运用形态学滤波滤除掉非光滑线段^[6]，进而得到光滑线段作为构成电力线的基元。第2个步骤运用统计学特征，提取电力线主方向，剔除无用的线段基元，保留真正的电力线线段基元，并拟合成为“真实”的电力线^[7]。

本文算法执行过程如如图1所示。

1.2 局部线段基元提取——LSD直线提取算法

LSD涉及到2个基本概念：梯度和图像的基准线(level-line)^[8]，如图2所示。LSD先计算每个像素与基准线的夹角以构建基准线场(level-line field)；然后利用区域生长算法合并场里方向近似一致的像素，得到一系列线支撑域(line support regions)，如图3所示；最后在这些域内进行像素合并提取直线段，并基于“Contrario model”和“Helmholtz principle”进行误差控制^[9]。

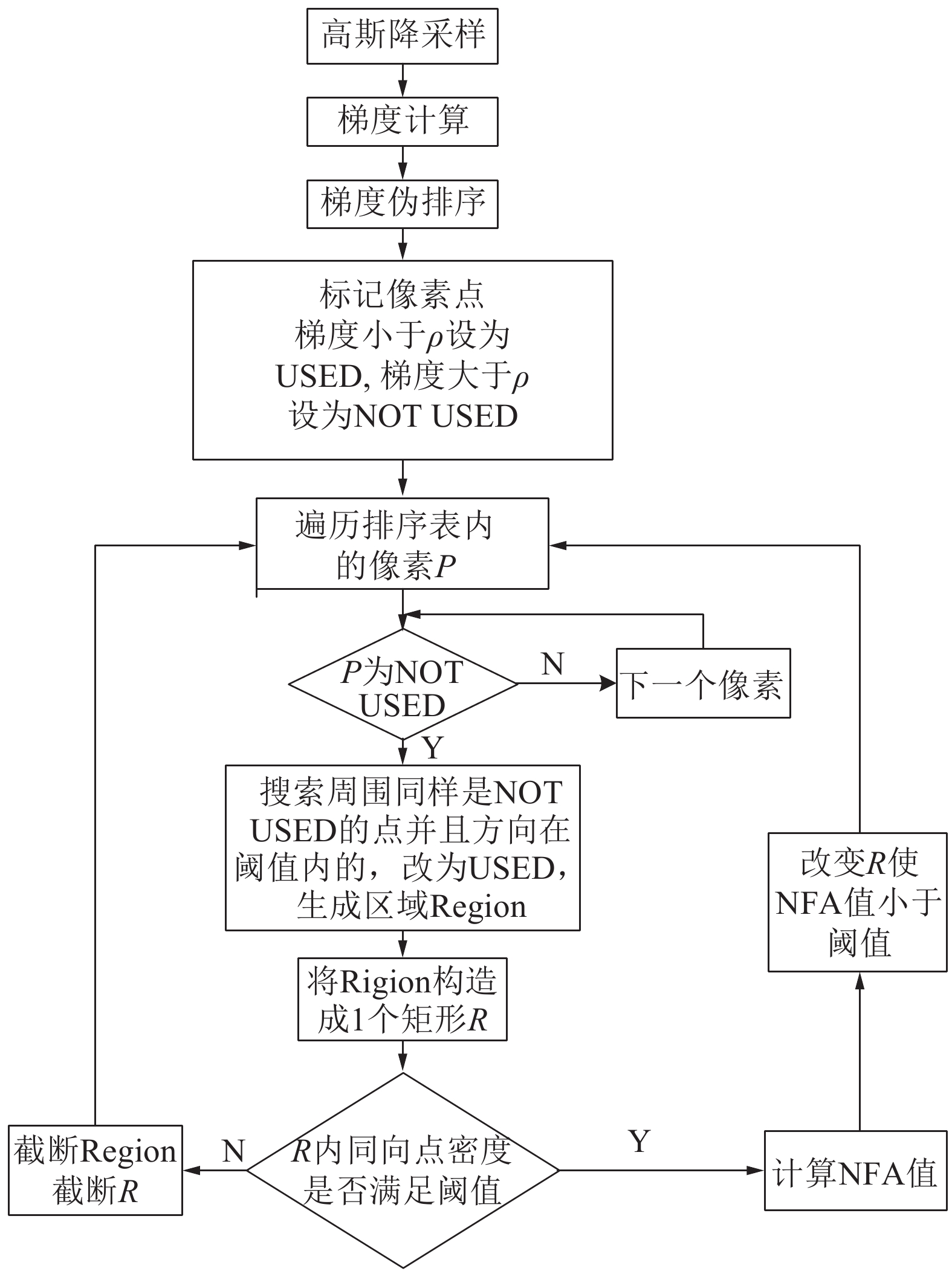
LSD算法流程如图4所示，经过LSD直线提取算法处理，可得所有检测出线段基元的左右端点及线段宽度^[10]。

但是LSD直线提取算法还存在一些问题^[11]，一方面，在真实图像中，往往由噪声和畸变等影响，致使直线变成有较小曲率的弧线；另一方面，从LSD像素合并和控制误差的准则可以看出，这种算法只对直线段有用，对其他线结构将失效，如弧段或折线等，即使是曲率较小的弧段也难以有效。而现在的电力线杆塔之间可能会存在较长距离，所以电力线会产生下垂，因此一根电力线在图像中会被识别为很多的较短的线段基元。

1.3 中层视觉感知聚集——统计学特征 1.3.1 主方向的提取

根据LSD算法提取的所有直线段的起点和终点，计算直线段的斜率进而得到线段倾角，然后统计每个倾角线段的长度之和，利用每个斜率直线段出现频率与线段长度之和的乘积排序，提取对应乘积最大的斜率作为主斜率，即电力线的主方向^[12]。

获取到主斜率之后，根据设置的容忍角度 $\sigma $ 筛选所有的线段基元，将与主方向夹角小于容忍角度的线段基元加入电力线线段基元池中。

1.3.2 基于侧向距离的线段基元的分析

计算每2个线段基元的侧向距离，判断这2个线段基元在原始图像中是否为同一条电力线，假设线段基元L₁左右端点为A、B，方程 ${A_1}x + {B_1}y + {C_1} = 0$ ；线段基元L₂的端点为C、D，方程为 ${A_2}x + {B_2}y + {C_2} = 0$ ，且A、B、C、D这4点坐标为 $A({a_1},{b_1}){\text 、}B({a_2},{b_2}){\text 、}C({a_3},{b_3}){\text 、}D({a_4},{b_4})$ 。

根据直线两点式方程，直线段L₁、L₂可分别表示为

$\frac{{x - {a_1}}}{{{a_2} - {a_1}}} = \frac{{y - {b_1}}}{{{b_2} - {b_1}}},\frac{{x - {a_3}}}{{{a_4} - {a_3}}} = \frac{{y - {b_3}}}{{{b_4} - {b_3}}} $

两点式转化为一般式得

$ \begin{aligned} & \frac{{{b_2} - {b_1}}}{{{a_2} - {a_1}}}x - y - \frac{{{a_1} \times {b_2} - {a_2} \times {b_1}}}{{{a_2} - {a_1}}} = 0\\ & \frac{{{b_4} - {b_3}}}{{{a_4} - {a_3}}}x - y - \frac{{{a_3} \times {b_4} - {a_4} \times {b_3}}}{{{a_4} - {a_3}}} = 0 \end{aligned} $

根据点到直线的距离公式可得，线段L₁中点到线段L₂的距离D₁为

$ \begin{aligned} & {D_1} = \left| {\frac{{{A_2} \times \displaystyle\frac{{\left( {{a_1} + {a_2}} \right)}}{2} + {B_2} \times \frac{{\left( {{b_1} + {b_2}} \right)}}{2} + {C_2}}}{{\sqrt {A_2^2 + B_2^2} }}} \right| = \\ & \left| {\frac{{\displaystyle\frac{{{b_4} - {b_3}}}{{{a_4} - {a_3}}} \times \frac{{\left( {{a_1} + {a_2}} \right)}}{2} + \left( { - 1} \right) \times \frac{{\left( {{b_1} + {b_2}} \right)}}{2} + \frac{{{a_3} \times {b_4} - {a_4} \times {b_3}}}{{{a_4} - {a_3}}}}}{{\sqrt {{{\left( {\displaystyle\frac{{{b_4} - {b_3}}}{{{a_4} - {a_3}}}} \right)}^2} + 1} }}} \right| \end{aligned} $

(1)

利用式（1）计算每个线段基元中点到其他线段基元所在直线的距离^[13]，然后对所有的距离进行排序。若线段基元和另一个基元所在直线距离小于一定阈值Thresh，则将2个线段基元归为一组。依次判断，完成线段基元的分组，并认为同属一组的线段基元属于同一电力线。同时统计大于一定阈值的线段基元，若存在线段基元和其他线段基元构成的直线的距离都大于一定的阈值，则判断该线段基元为恰好在主方向范围内的非电力线线段基元，将其剔除出线段基元池。

由于电力线通常连续且贯穿图像，检测出的线段基元应较为密集，因此由少量线段基元构成的线段基元分组，不满足构成图像中的电力线的条件，视为非电力线的干扰线段组，剔除出线段基元池。

经过基元分组及2次干扰线段剔除，可得到准确的电力线段基元及其分组。

1.3.3 最小二乘法拟合

由于电力线弧垂的存在^[14]，导致电力线并非是严格意义上的直线，而呈现悬链线形态，所以对电力线的拟合不能采用直线拟合模型。因此，本文采用多项式曲线拟合的方法^[15]，即拟合曲线方程为n阶多项式

$ y = {\kern 1pt} {\sum\nolimits_{i = 0}^n a _i}{x^i} = {a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + \cdots + {a_1}x + {a_0} $

用矩阵形式表示为 ${{Y}} = {{{X}}_0}{{A}}$ 。

式中：

$ {{{X_0}}} = \left[ {\begin{array}{*{20}{c}} {x_1^n}&{x_1^{n - 1}}&\cdots&{x_1^2}&{{x_1}}&1\\ {x_2^n}&{x_2^{n - 1}}& \cdots &{x_2^2}&{x_2^{}}&1\\ \vdots & \cdots & \cdots &\cdots & \cdots &\vdots \\ {x_k^n}&{x_k^{n - 1}}& \cdots &{x_k^2}&{x_k^{}}&1 \end{array}} \right] $

(2)

待求解项为系数向量：

$ {{A}} = {\left[ {{a_n},{a_{n - 1}}, \cdots ,{a_2},{a_1},{a_0}} \right]^{\rm{T}}} $

曲线拟合方程 ${{Y}} = {{{X}}_0}{{A}}$ 的求解方法与上述直线的求解方法类似，在方程 ${{Y}} = {{{X}}_0}{{A}}$ 两边同时乘以 ${{{X}}_0}$ 的转置矩阵，得到 ${{X}}_{{\rm{0}}}^{\rm{T}}{{Y}} = {{X}}_{{\rm{0}}}^{\rm{T}}{{{X}}_0}{{A}}$ ，再同时在新方程两边乘 ${{X}}_{{\rm{0}}}^{\rm{T}}{{{X}}_0}$ 的逆矩阵，得到 ${({{X}}_{_0}^T{{{X}}_0})^{ - 1}}{{X}}_{0}^T{{Y}} = {{A}}$ 。

式(2)等号左边各部分均已知，所以可直接求解得拟合曲线方程的系数向量A，进而完成航拍图像中的电力线的拟合，并能根据拟合结果准确提取电力线。

2 实验结果和分析

本文选取了20幅不同场景、不同形态的输电线路航拍图像作为实验数据，对算法进行测试，并与传统Canny与Hough算法^[16]进行对比。经过反复实验，本文算法实验参数设置为：主方向筛选容忍角度 $\sigma $ 设为±20°；侧向距离阈值Thresh设为10 pix。曲线拟合中，曲线方程阶数 $n$ 取3，因为阶数为3既可保证电力线呈悬链线时的检测精度，又可保证检测时的计算速率。

2.1 定性分析

从每种场景中各选取一副电力线检测效果进行显示，为了直观地展示电力线分割效果，将不同算法的分割结果与原图像叠加。图5为在电力线上方垂直下拍的电力线，图6~9为电力公司提供的山区电力线航拍图。

2.2 定量分析

图10为分别通过对20幅测试图绘制电力线单像素宽度的真值图，利用平均识别率（R_C）和误检率（R_E）对本文算法和传统算法进行检测精度的定量分析。

$ {R_C} = \frac{{{N_{{\rm{correct}}}}}}{{{N_{{\rm{all}}}}}},{R_E} = \frac{{{N_{{\rm{error}}}}}}{{{N_{{\rm{all}}}}}} $

式中： ${N_{{\rm{correct}}}}$ 为检测的正确像素点数； ${N_{{\rm{all}}}}$ 为检测的所有像素点数； ${N_{{\rm{error}}}}$ 为错误检测的像素点数。

本文算法与利用Canny算子和Hough变换的检测方法对20幅测试图像的平均检测结果如表1所示。

可以看出，利用Canny算子和Hough变换的检测方法，在背景复杂的情况下，电力线提取效果较差，会提取出背景中各种类似线段的非电力线线段基元，并且随着电力线的弯曲，出现电力线断裂和提取不全等问题。而本文算法在不同背景下，对直线形态和悬链线形态的电力线提取效果准确。通过以上对比可以看出，本文算法能在多种场景下准确完成直线与悬链线2种形态输电线的提取。

3 结论

本文提出了一种基于LSD算法的航拍图像电力线提取方法，利用统计学特征和最小二乘法对LSD算法提取的线段基元进行筛选和拟合，完成电力线的提取。实验表明，该算法可完成不同背景下不同形态、不同方向的电力线检测，与现有方法相比，本文算法在准确度和稳定性上均有提升，其中识别率达到75.2%，比同类算法提高9.8%，误检率为10.3%，比同类算法低29.8%，具有更高的精度、抗噪性、可靠性。

但由于该算法根据统计概率限定了电力线的主方向，对于多方向电力线的航拍图将产生漏检现象。针对该算法的不足，在未来的工作中，本文将对多方向交叉电力线的提取问题进行进一步研究。