2. 深圳大学 光电工程学院, 广东 深圳 518054;
3. 深圳技术大学 中德智能制造学院, 广东 深圳 518054
2. College of Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China;
3. Sino-German College for Intelligent Manufacturing, Shenzhen Technology University, Shenzhen 518060, China
陀螺仪是用于测量角速度的惯性传感器,是惯导系统中的重要组成部分,陀螺仪的精度直接影响了惯导系统的性能。光纤陀螺仪与传统的机械陀螺相比,具有无旋转部件、耐冲击、使用寿命长、检测精度高、动态范围大等优势。与第一代光学陀螺即激光陀螺相比,光纤陀螺制造成本低,加工工艺简单,能根据使用对象的要求,实现不同精度的产品,可应用于更广阔的领域[1-2]。近年来,干涉型光纤陀螺和谐振型光纤陀螺有着广泛的应用[3-8],其研究是目前国际上相当热门的课题,光纤陀螺正在向越来越高精度的方向发展。因此,研究光纤陀螺仪的相关参数变化是其重要的理论组成基础。
光纤陀螺是基于光学Sagnac效应的一种高精度角速度传感器,相位差Δφ和谐振频率差Δνq是Sagnac效应的2个重要参数,它们都可以表征光纤陀螺系统相对于惯性空间的角速度Ω。许多文献采用了不同的方法对这2个参数关于角速度Ω的表达式进行推导[9-14],但是对谐振频率差的推导过程不够详细。本文提供了光纤陀螺中的相位差Δφ和的谐振频率差Δνq较为详细的推导过程,以及它们二者之间所满足的关系,并分别从数学形式和物理意义对这一关系作出分析,为光纤陀螺方面的研究者提供了理论参考和依据。
1 光纤陀螺的工作原理简析光纤陀螺的光纤环结构如图 1所示。

|
Download:
|
| 图 1 Sagnac效应 | |
当光纤陀螺系统相对于惯性空间旋转(转动线速度RΩ相对于真空光速c而言很小,即RΩ ≪ c)时,光纤内顺时针传播的光波(CW光)与逆时针传播的光波(CCW光)绕行一周返回出发点时所需要的时间并不相等,它们分别记为tcw和tccw,即它们的时间差Δt=tcw-tccw ≠ 0,而且是正比于角速度Ω。时间差Δt导致光纤陀螺中的相位差Δφ和谐振频率差Δνq都不为0,这2个重要的参数都与时间差Δt有关。
先求出顺逆时针传播的两束光波的时间差Δt关于角速度Ω的表达式,通过时间差Δt与相位差Δφ和谐振频率差Δνq这2个重要参数的关系,从而求得这2个参数关于角速度Ω的表达式。
在求解顺逆时针传播的两束光波的时间差Δt的过程中,将会涉及到2个参考系(光纤环参考系和惯性空间参考系)的转换问题。对于低速运动的物体,不同参考系之间速度的转换可以使用经典力学中的伽利略速度合成公式;而对于高速运动的物体,不同参考系之间速度的转换需要使用相对论中的洛伦兹速度转换公式。有些文献同时使用了经典力学的伽利略速度合成公式和相对论中的洛伦兹速度转换公式[10],本文在遇到不同参考系速度转换的问题时,将统一使用相对论中的洛伦兹速度转换公式进行不同参考系之间速度的转换,从而使光纤陀螺方面的研究者能更好地理解这个推导过程。
2 圆形光路中顺逆时针传播的两束光波的时间差众所周知,无论在真空中还是在介质中,光在空间中走过的光程δ等于真空光速c乘以光在空间中的传播时间t,即
| $ \delta = ct $ | (1) |
这是在任意情况下都能满足的光程计算式。
在选定参考系的情况下,如果光在真空中传播,那么光程δ=d,其中d为光在空间中走过的路程;如果光在折射率为n的介质中传播,而且该介质相对于所选参考系静止,那么光程δ同时也等于介质折射率n与光在空间中走过的路程d的乘积,即
| $ \delta = nd $ | (2) |
此时可通过将路程d代入式(2)求得光程δ。但是,如果该介质相对于所选参考系运动,那么式(2)将不再适用。由于式(1)的适用范围比式(2)要大,因此当光在介质中传播时,我们在计算光程时将采用式(1),而避免使用式(2)。
在一个任意几何形状的闭合光学环路中,从任意一点发出的沿相反方向传播的两束光波,绕行一周返回到该点时,如果闭合回路相对惯性空间以Ω为角速度发生旋转,则两束光波的光程差Δδ或时间差Δt与Ω有关,这称为Sagnac效应[10]。光程差Δδ等于真空光速c与时间差Δt的乘积,即
| $ \Delta \delta = c\Delta t $ | (3) |
由于光程差与时间差的区别仅为一个系数c,因此在实际中,讨论光程差等价于讨论时间差。下面我们就对两束光波的时间差Δt关于角速度Ω的表达式作进一步讨论。
如图 1(a)所示,一个半径为R的闭合圆形光路在静止状态下,从点M同时发出两束光波分别沿环形光路顺、逆时针相向传播,两束光经过相同的路程后将同时回到点M,其时间差Δt为零,CCW路光波和CW路光波的传输时间tcw和tccw相等[11],即tcw=tccw=t0,其中t0为Sagnac效应敏感环静止时光顺时针或逆时针传播整整一周的时间,此时Δt=tcw-tccw=0。
如图 1(b)所示,当光路系统以角速度Ω相对惯性空间转动时,因为Sagnac效应敏感环(光纤环)的转动线速度RΩ相对于光速c而言很小,即RΩ ≪ c,所以在推导的过程中,考虑到:
1) Sagnac效应敏感环从点M转到点M1的时间记为t,光逆时针从点M传播到点M1的时间(略小于一周,CCW路光波少走了弧
2) 实际上,tcw和tccw并不完全相等,时间差Δt=tcw-tccw相比于t0而言很小(Δt ≪ t0)但Δt ≠ 0,两路光波实际上并非同时到达点M1,而是先后到达点M1。又由于光纤环和点M相对于惯性空间处于转动状态,所以两束光波所到达的点M1并非同一个点,这两个点分别记为M1cw和M1ccw,考虑到光纤环转动线速度RΩ远远小于光速c,因此在这里可认为点M1cw和M1ccw近似重合,即点M1。
综合上述考虑,我们在进行理论分析时,可以采用以下的近似关系:tcw+tccw≈2t0和tcwtccw≈t02。
2.1 真空中的时间差假设真空中圆形光路为N匝(图 1表示N=1这一特殊情况),并记1匝闭合光路的长度为L,围成的面积为S,则整个(N匝)闭合光路的总长度为NL,围成的总面积为NS,则t0=NL/c。当光路系统以角速度Ω相对惯性空间转动时,那么两束相向传输的光波到达点M1时所经历的光程将不同。与Ω反向传播的光波经过环形光路到达点M1的时候,该光波所走过的路程(真空中,光程=路程)比环形光路的周长要短,其大小为[11]
| $ {L_{{\rm{ccw}}}} = NL - R\mathit{\Omega }{t_{{\rm{ccw}}}} = c{t_{{\rm{ccw}}}} $ | (4) |
同理,与Ω同向传播的光波到达点M1时路程比环形光路的周长要长,其大小为
| $ {L_{{\rm{cw}}}} = NL + R\mathit{\Omega }{t_{{\rm{cw}}}} = c{t_{{\rm{cw}}}} $ | (5) |
这里讨论路程时所选取的参考系仍然是惯性空间,式(4)与式(5)采用了路程叠加法,并未涉及到参考系转换问题。以下列出求时间差Δt的2种方法:
1) 采用近似关系tcw+tccw≈2t0,由式(4)、(5)可得
| $ \begin{array}{l} \Delta t = {t_{{\rm{cw}}}} - {t_{{\rm{ccw}}}} = \frac{{{L_{{\rm{cw}}}} - {L_{{\rm{ccw}}}}}}{c} = \frac{{({t_{{\rm{cw}}}} + {t_{{\rm{ccw}}}})R\mathit{\Omega }}}{c} \approx \\ \;\;\;\;\;\;\;\;\;\frac{{2{t_0}R\mathit{\Omega }}}{c} = \frac{{2NLR\mathit{\Omega }}}{{{c^2}}} = \frac{{4NS}}{{{c^2}}}\mathit{\Omega } \end{array} $ | (6) |
2) 由式(4)与式(5)可得
| $ {t_{{\rm{cw}}}} = \frac{{NL}}{{c - R\mathit{\Omega }}} $ | (7) |
| $ {t_{{\rm{ccw}}}} = \frac{{NL}}{{c + R\mathit{\Omega }}} $ | (8) |
可发现式(7)与(8)的结果等价于直接使用经典力学中的伽利略速度合成公式,这就是有些文献直接使用经典力学计算此过程的缘故。采用近似关系RΩ ≪ c,可得
| $ \begin{array}{l} \Delta t = {t_{{\rm{cw}}}} - {t_{{\rm{ccw}}}} = \frac{{NL}}{{c - R\mathit{\Omega }}} - \frac{{NL}}{{c + R\mathit{\Omega }}} = \\ \;\;\frac{{2NLR\mathit{\Omega }}}{{{c^2} - {{\left( {R\mathit{\Omega }} \right)}^2}}} \approx \frac{{2NLR\mathit{\Omega }}}{{{c^2}}} = \frac{{4NS}}{{{c^2}}}\mathit{\Omega } \end{array} $ | (9) |
对比式(6)与式(9)发现,2种方法所得的时间差Δt相同。
2.2 介质中的时间差假设介质中圆形光路(光纤环)仍为N匝,则t0=NLn/c,其中n为有效折射率,光路系统仍以角速度Ω相对惯性空间旋转。
对于高速运动的物体,不同参考系之间速度的转换需要使用相对论中的洛伦兹速度转换公式[15-18],设有3个物体A、B和C,已知物体A相对于物体B的速度为uAB,物体B相对于物体C的速度为uBC,则物体A相对于物体C的速度uAC满足如下洛伦兹速度转换公式:
| $ {u_{AC}} = \frac{{{u_{AB}} + {u_{BC}}}}{{1 + \frac{{{u_{AB}}{u_{BC}}}}{{{c^2}}}}} $ | (10) |
由于光相对于光纤的速度为c/n,光纤环相对于惯性空间的线速度为RΩ,若顺时针和逆时针传播的光相对于惯性空间的速度分别记为ucw和uccw,根据洛伦兹速度转换公式(10)则有
| $ \begin{array}{l} {u_{{\rm{cw}}}} = \frac{{c/n + R\mathit{\Omega }}}{{1 + \frac{{c/n \cdot R\mathit{\Omega }}}{{{c^2}}}}}\\ {u_{{\rm{ccw}}}} = \frac{{c/n - R\mathit{\Omega }}}{{1 - \frac{{c/n \cdot R\mathit{\Omega }}}{{{c^2}}}}} \end{array} $ |
根据数学公式麦克劳林展开式
| $ \begin{array}{l} \frac{1}{{1 + x}} = 1 - x + {x^2} - {x^3} + {x^4} - \cdots \left( {|x| < 1} \right)\\ \frac{1}{{1 - x}} = 1 + x + {x^2} + {x^3} + {x^4} + \cdots \left( {|x| < 1} \right) \end{array} $ |
采用近似关系RΩ ≪ c略去RΩ的高次项,只保留常数项和RΩ的一次项,分别对ucw和uccw进行化简。
| $ \begin{array}{*{20}{c}} {{u_{{\rm{cw}}}} = \frac{{c/n + R\mathit{\Omega }}}{{1 + \frac{{c/n \cdot R\mathit{\Omega }}}{{{c^2}}}}} = }\\ {\left( {\frac{c}{n} + R\mathit{\Omega }} \right) \cdot 1\left[ { - \frac{{\frac{c}{n} \cdot R\mathit{\Omega }}}{{{c^2}}} + {{\left( {\frac{{\frac{c}{n} \cdot R\mathit{\Omega }}}{{{c^2}}}} \right)}^2} - \cdots } \right] = }\\ {\frac{c}{n} + R\mathit{\Omega } - \frac{c}{n} \cdot \frac{{\frac{c}{n} \cdot R\mathit{\Omega }}}{{{c^2}}} - R\mathit{\Omega } \cdot \frac{{\frac{c}{n} \cdot R\mathit{\Omega }}}{{{c^2}}} + }\\ {\frac{c}{n} \cdot {{\left( {\frac{{\frac{c}{n} \cdot R\mathit{\Omega }}}{{{c^2}}}} \right)}^2} + \cdots = \frac{c}{n} + R\mathit{\Omega }\left( {1 - \frac{1}{{{n^2}}}} \right) - }\\ {{{\left( {R\mathit{\Omega }} \right)}^2} \cdot \frac{{\left( {1 - \frac{1}{{{n^2}}}} \right)}}{{cn}} + \cdots \approx \frac{c}{n} + R\mathit{\Omega }\left( {1 - \frac{1}{{{n^2}}}} \right)} \end{array} $ | (11) |
同理可得
| $ {u_{{\rm{ccw}}}} = \frac{{c/n - R\mathit{\Omega }}}{{1 - \frac{{c/n \cdot R\mathit{\Omega }}}{{{c^2}}}}} \approx \frac{c}{n} - R\mathit{\Omega }\left( {1 - \frac{1}{{{n^2}}}} \right) $ | (12) |
在惯性空间参考系下,同理采用路程叠加法可得
| $ {L_{{\rm{cw}}}} = NL + R\mathit{\Omega }{t_{{\rm{cw}}}} = {u_{{\rm{cw}}}}{t_{{\rm{cw}}}} $ | (13) |
| $ {L_{{\rm{ccw}}}} = NL - R\mathit{\Omega }{t_{{\rm{ccw}}}} = {u_{{\rm{ccw}}}}{t_{{\rm{ccw}}}} $ | (14) |
与光在真空中传播的情况一样,对于光在介质中传播的情况,由式(13)与式(14)可得
| $ {t_{{\rm{cw}}}} = \frac{{NL}}{{{u_{{\rm{cw}}}} - R\mathit{\Omega }}} $ | (15) |
| $ {t_{{\rm{ccw}}}} = \frac{{NL}}{{{u_{{\rm{ccw}}}} + R\mathit{\Omega }}} $ | (16) |
同理,可发现式(15)与式(16)的结果也等价于直接使用经典力学中的伽利略速度合成公式。将式(11)与式(12)分别代入到式(15)与式(16),并采用近似关系RΩ ≪ c,可得
| $ \begin{array}{*{20}{c}} {\Delta t = {t_{{\rm{cw}}}} - {t_{{\rm{ccw}}}} = \frac{{NL}}{{{u_{{\rm{cw}}}} - R\mathit{\Omega }}} - \frac{{NL}}{{{u_{{\rm{ccw}}}} + R\mathit{\Omega }}} = }\\ {\frac{{NL}}{{\frac{c}{n} + R\mathit{\Omega }\left( {1 - \frac{1}{{{n^2}}}} \right) - R\mathit{\Omega }}} - \frac{{NL}}{{\frac{c}{n} - R\mathit{\Omega }\left( {1 - \frac{1}{{{n^2}}}} \right) + R\mathit{\Omega }}}}\\ { = \frac{{NL}}{{\frac{c}{n} - \frac{{R\mathit{\Omega }}}{{{n^2}}}}} - \frac{{NL}}{{\frac{c}{n} + \frac{{R\mathit{\Omega }}}{{{n^2}}}}} = \frac{{2NLR\mathit{\Omega } \cdot \frac{1}{{{n^2}}}}}{{{{\left( {\frac{c}{n}} \right)}^2} - {{\left( {\frac{{R\mathit{\Omega }}}{{{n^2}}}} \right)}^2}}} \approx }\\ {\frac{{2NLR\mathit{\Omega } \cdot \frac{1}{{{n^2}}}}}{{{{\left( {\frac{c}{n}} \right)}^2}}} = \frac{{2NLR\mathit{\Omega }}}{{{c^2}}} = \frac{{4NS}}{{{c^2}}}\mathit{\Omega }} \end{array} $ | (17) |
对比真空中所得结果式(6)或式(9)与介质中所得结果式(17)可进一步发现,无论是在真空中,还是在介质中,时间差Δt都相同,与有效折射率n无关。此外,时间差Δt与匝数N成正比,这是由于两路光波从M点出发回到M1点的传播时间tcw和tccw都与匝数N成正比。同时,时间差Δt与光路围成的总面积成正比。
对于绕任意轴转动的任意几何形状的闭合曲线的环形光路,闭合曲线构成的曲面的法向量与旋转轴存在一个夹角θ,利用微积分方法[19],同样可以求得与式(17)类似的结果,此时时间差为
| $ \Delta t = {t_{{\rm{cw}}}} - {t_{{\rm{ccw}}}} = \frac{{4N}}{{{c^2}}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \frac{{4NS\cos \theta }}{{{c^2}}}\mathit{\Omega } $ | (18) |
式中S为曲面面积矢量(法向量方向),Ω为角速度矢量,对比式(17)和式(18)可发现,式(18)考虑了两矢量夹角非平行的情况。可见时间差Δt还与该夹角θ的余弦值成正比。将上述时间差Δt代入到式(3)中可得,光程差为
| $ \Delta \delta = c\Delta t = \frac{{4N}}{c}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \frac{{4NS\cos \theta }}{c}\mathit{\Omega } $ | (19) |
由式(19)可知,光程差Δδ同样也与有效折射率n无关,而与匝数N成正比。
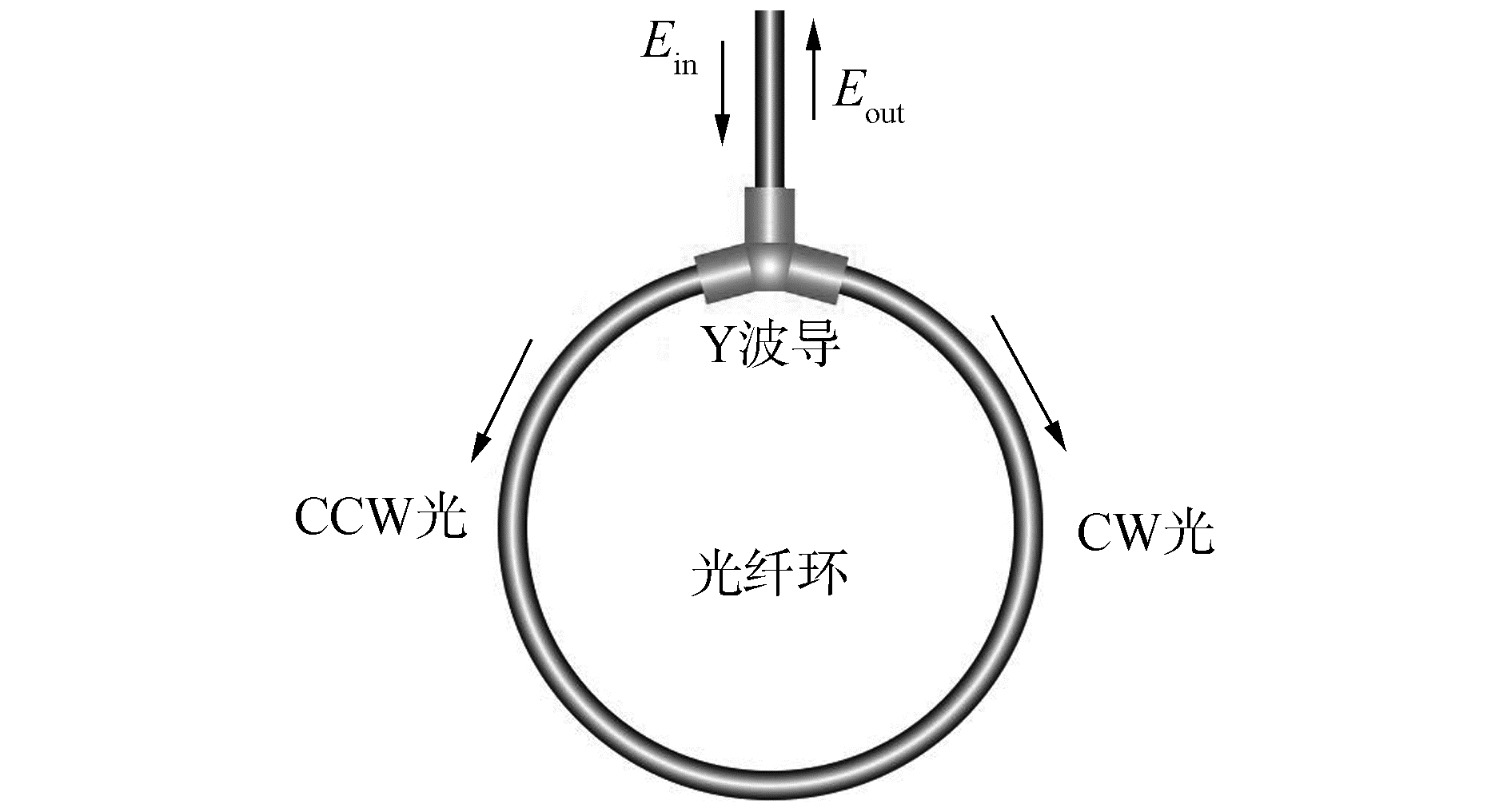
3 光纤陀螺的相位差设顺时针和逆时针传播的两路光波都具有相同的频率,且频率保持恒定为ν0,对应的真空波长记为λ0。在图 1中,为了保证两路光频率保持恒定且从M点出发传播到M1点后没有继续在环内传播,而是实现两路光发生双光束干涉并输出,那么需要在光出发点(M点)处接上一个Y波导,如图 2所示。
|
Download:
|
| 图 2 光纤环形干涉仪 | |
由于两路光频率相等,因此它们在光纤中相移之差,称为同频相位差(简称相位差)。相位差Δφ等于角频率2πν0乘以时间差Δt,由c=λ0ν0可知,由两束光波的传输时间差Δt所引起的相位差Δφ为[19-22]
| $ \Delta \varphi = \frac{{2{\rm{ \mathsf{ π} }}c}}{{{\lambda _0}}}\Delta t = \frac{{2{\rm{ \mathsf{ π} }}c}}{{{\lambda _0}}} \cdot \frac{{4N}}{{{c^2}}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \frac{{8{\rm{ \mathsf{ π} }}N}}{{{\lambda _0}c}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (20) |
由式(20)可知,Sagnac效应是一种与介质无关的纯空间延迟,有效折射率n对Sagnac相移Δφ没有影响;Sagnac相移Δφ仅与整个闭合光路的总面积NS和旋转角速率Ω成正比[12]。
另外,由于光速c很大,相位差Δφ很小,为提高对角速度的检测精度,须增大Δφ,那么可以增大线圈匝数N的方法来增大Δφ。
干涉型光纤陀螺正是利用两路光波的相位差Δφ来表征系统的旋转角速度Ω。
4 光纤陀螺的谐振频率差设介质中圆形光路(光纤环)为N匝,在图 1中,为了使得光波从M点出发传播到M1点时与原来的光波发生干涉,光出发点(M点)处接上一个耦合器,使得该耦合器与光纤环构成谐振腔,整个光路系统仍以角速度Ω相对惯性空间旋转。定义νcwq和νccwq为CW路光波和CCW路光波的谐振频率,其中q为光波纵模模式数。
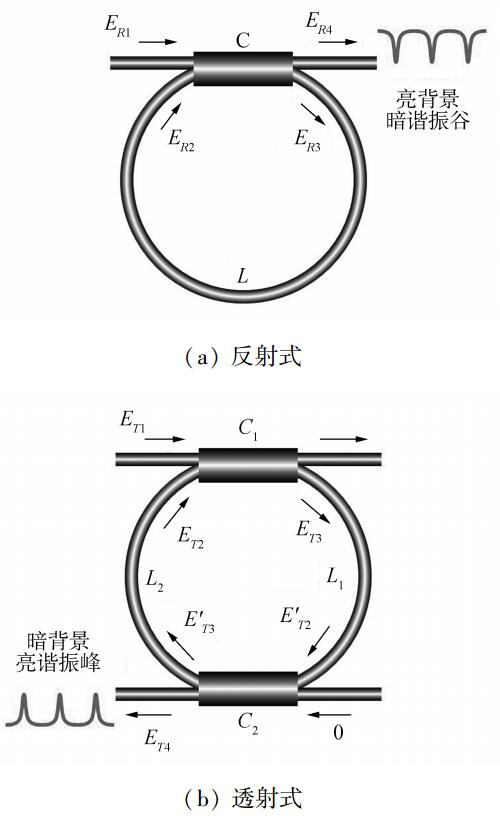
但是,为了便于光的输入和输出,需要将光纤环上的耦合器的另外两个端口作为输入端和输出端;或在光纤环上再接上第2个耦合器,其一端作为输出端,而原耦合器的一端作为输入端。图 3给出了2种接法,分别为图 3(a)的反射式接法和图 3(b)的透射式接法。
|
Download:
|
| 图 3 光纤环形谐振腔 | |
光纤环静止时CW路光波和CCW路光波的谐振谷重合,CW路光波和CCW路光波共用同一个谐振频率νq,即两路光波在腔内同属于第q个纵模,共用同一个整数q;光纤环相对于惯性空间旋转时,虽然CW路光波和CCW路光波的谐振谷都发生频移,但整数q不变(即与光纤环静止时对应的整数q相等)。
由此可见两路光波的谐振频率并不完全相等,故它们在光纤中相移之差不是同频相位差。当两路光波的频率都取谐振频率时,它们在腔内都发生谐振,此时两路光波在光纤中相移之差,称为谐振相位差。利用谐振条件所得到的两束光波的纵模模式数都是整数q,可知腔内两路谐振光波的相移都是2qπ。因此,在光纤陀螺中,谐振相位差Δφq=2qπ-2qπ=0,即与系统的旋转角速率Ω无关,显然此时讨论谐振相位差没有意义,它不能用来表征角速度Ω。
但是,我们可以利用谐振频率差Δνq=νccwq-νcwq来表征角速度Ω。谐振型光纤陀螺正是利用这一工作机理测量系统的旋转角速度Ω。
4.1 基于激光物理学中的行波谐振腔理论求谐振频率差由上述νcwq和νccwq的定义,则可知νcwq-1为满足谐振条件时CW路光波相位改变2π的时间,定义该时间为CW路光波的谐振周期;同理,νccwq-1为CCW路光波的谐振周期。
在图 1(b)中,若光波从M点出发传播到M1点时刚好与原来的光波相长(即光波从M点出发传播到M1点所需要的时间等于光波的谐振周期的整数倍),则光在腔内会出现谐振现象。谐振条件可以写为
| $ {t_{{\rm{cw}}}} = q \cdot \nu _{{\rm{cwq}}}^{ - 1} $ | (21) |
| $ {t_{{\rm{ccw}}}} = q \cdot \nu _{{\rm{ccwq}}}^{ - 1} $ | (22) |
则由式(18)、(21)和(22),并采用近似关系tcwtccw≈t02,可求得顺逆时针两束光波的谐振频率差为
| $ \begin{array}{l} \Delta {\nu _q} = {\nu _{{\rm{ccw}}q}} - {\nu _{{\rm{cw}}q}} = q\left( {\frac{1}{{{t_{{\rm{ccw}}}}}} - \frac{1}{{{t_{{\rm{cw}}}}}}} \right) = q \cdot \frac{{\Delta t}}{{{t_{{\rm{ccw}}}}{t_{{\rm{cw}}}}}} \approx \\ \;\;\;\;q \cdot \frac{{\Delta t}}{{t_0^2}} = q \cdot \frac{{\frac{{4N}}{{{c^2}}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}{{{{\left( {\frac{{NL}}{{c/n}}} \right)}^2}}} = q \cdot \frac{4}{{N{n^2}{L^2}}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{array} $ | (23) |
CW路光波和CCW路光波在腔内属于同第q个纵模,共用同一个整数q;光纤环相对于惯性空间旋转时,虽然CW路光波和CCW路光波的谐振谷都发生频移,但整数q不变(即与光纤环静止时对应的整数q相等)。光纤环静止时,根据激光物理学中行波谐振腔的理论,当谐振腔的腔长刚好等于光波波长的整数倍时,将会出现谐振现象[20],则光纤环静止时的谐振条件为
| $ q \cdot \frac{{{\lambda _0}}}{n} = NL $ | (24) |
由式(24)可推出
| $ q = \frac{{NnL}}{{{\lambda _0}}} $ | (25) |
将式(25)代入式(23)即可求出光路系统以角速度Ω相对惯性空间旋转时顺逆时针两束光波的谐振频率差[2-23]
| $ \Delta {\nu _q} = \frac{{NnL}}{{{\lambda _0}}} \cdot \frac{4}{{N{n^2}{L^2}}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \frac{4}{{n{\lambda _0}L}}\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (26) |
当光纤环为任意封闭曲面时,谐振频率差则由式(26)提供。由该式可知两路光波的谐振频率差Δνq与匝数N无关,但与物体的转动角速度Ω成正比,转动的角速度Ω越大,则谐振频率差Δνq越大,因此可以通过测量谐振频率差来计算物体的转动角速度[24]。
定义参数D=4Scos θ/L。谐振频率差也可写为
| $ \Delta {\nu _q} = \frac{{4S\cos \theta }}{{n{\lambda _0}L}}\mathit{\Omega } = \frac{D}{{n{\lambda _0}}}\mathit{\Omega } $ | (27) |
通常情况下,式(27)中的夹角θ为0°,即系统相对于惯性空间转动的旋转轴垂直于闭合曲线构成的曲面。在θ=0°的情况下,当闭合光路为圆形时,则式(27)中的D表示该圆的直径;当闭合光路为多边形时,若该多边形存在内切圆(该内切圆与多边形的每一条边都相切),则D表示该内切圆的直径。
4.2 基于多光束干涉机理求谐振频率差首先,谐振腔中光波的角频率和频率分别记为ω和ν,即满足ω=2πν。
对于反射式谐振型光纤陀螺,如图 3(a)所示,入射光波从R1端经耦合器C后分成两束,一束光波从R4端直接输出,另一束光波从R3端进入环形光纤谐振腔,腔内的光传播一周后,由R2端再次进入耦合器C并与来自R1端的入射光发生干涉,其中一部分光波从R4端输出,余下的一部分光波又从R3端进入环形光纤谐振腔,继续在腔内传播,如此循环往复,每在谐振腔传播一周后,都有一部分光波从耦合器C的R4端输出,这样,通过直通端到达R4端的光和光纤环中不断耦合到达R4端的光发生多光束干涉,R4端的输出实际上是一种多光束干涉光波。
设耦合器C直通端与交叉端口的光功率耦合比为k:(1-k);由耦合器C的插入损耗和光纤环L的传输损耗所引起的光功率剩余百分比分别为ρC和ρL;光在光纤环L中的传输时间为t。考虑到光波每次从R1端到达R3端和从R2端到达R4端相位都将会改变π/2,则各个端口输出可表示为
| $ {E_{{R_2}}} = \sqrt {{\rho _L}} {{\rm{e}}^{ - {\rm{j}}\omega t}}{E_{{R_3}}} $ | (28) |
| $ {E_{{R_3}}} = j\sqrt {\left( {1 - k} \right){\rho _C}} {E_{{R_1}}} + \sqrt {k{\rho _C}} {E_{{R_2}}} $ | (29) |
| $ {E_{{R_4}}} = \sqrt {k{\rho _C}} {E_{{R_1}}} + j\sqrt {\left( {1 - k} \right){\rho _C}} {E_{{R_2}}} $ | (30) |
联立式(28)至(30)可得R4端与R1端的光场复振幅之比为
| $ \frac{{{E_{{R_4}}}}}{{{E_{{R_1}}}}} = \sqrt {k{\rho _C}} - \frac{{\left( {1 - k} \right){\rho _C}\sqrt {{\rho _L}} }}{{{{\rm{e}}^{{\rm{j}}\omega t}} - \sqrt {k{\rho _C}{\rho _L}} }} $ | (31) |
对式(31)左右两边取模的平方,可得R4端与R1端的光功率比
| $ {\left| {\frac{{{E_{{R_4}}}}}{{{E_{{R_1}}}}}} \right|^2} = {\rho _C}\left[ {1 - \frac{{\left( {1 - k} \right)\left( {1 - {\rho _C}{\rho _L}} \right)}}{{1 + k{\rho _C}{\rho _L} - 2\sqrt {k{\rho _C}{\rho _L}} \cos \omega t}}} \right] $ | (32) |
由式(32)可知,只有满足一定光频率的光才能产生谐振,当R1端入射光频率随时间线性变化时,R4端输出的谐振曲线呈现为亮背景下的暗谷,暗谷处表征光在腔内发生谐振,所以要使得|E4/E1|2取最小值,从而求出光纤谐振环的谐振条件,即cos ωt应取最大值。
对于透射式谐振型光纤陀螺,如图 3(b)所示,入射光波从T1端经耦合器C1后分成两束,一束光波从T3端进入环形光纤谐振腔,腔内有耦合器C2,使得腔内一部分光从T4端输出,另一部分光仍在腔内继续传播,腔内的光传播一周后,由T2端再次进入耦合器C1并与来自T1端的入射光发生干涉,干涉后一部分光波又从T3端进入环形光纤谐振腔,继续在腔内传播,如此循环往复,每在谐振腔传播一周的过程中,都有一部分光波从耦合器C2的T4端输出,这样,T4端的输出实际上是一种多光束干涉光波。
设耦合器C1和C2的直通端与交叉端口的光功率耦合比分别为k1:(1-k1)和k2:(1-k2);由两个耦合器C1和C2的插入损耗和两段光纤环L1和L2的传输损耗所引起光功率剩余百分比分别为ρC1、ρC2、ρL1和ρL2;光在两段光纤环L1和L2中的传输时间分别为t1和t2。考虑到光波每次从T1端到达T3端和从T2'端到达T4端相位都将会改变π/2,则各个端口输出可表示为
| $ E{'_{{T_2}}} = \sqrt {{\rho _{{L_1}}}} {{\rm{e}}^{ - {\rm{j}}\omega {t_1}}}{E_{{T_3}}} $ | (33) |
| $ {E_{{T_2}}} = \sqrt {{\rho _{{{\rm{L}}_2}}}} {{\rm{e}}^{ - {\rm{j}}\omega {t_2}}}E{'_{{T_3}}} $ | (34) |
| $ {E_{{T_3}}} = j\sqrt {\left( {1 - {k_1}} \right){\rho _{{C_1}}}} {E_{{T_1}}} + \sqrt {{k_1}{\rho _{{C_1}}}} {E_{{T_2}}} $ | (35) |
| $ E{'_{{T_3}}} = \sqrt {{k_2}{\rho _{{C_2}}}} E{'_{{T_2}}} $ | (36) |
| $ {E_{{T_4}}} = j\sqrt {\left( {1 - {k_2}} \right){\rho _{{C_2}}}} E{'_{{T_2}}} $ | (37) |
联立式(33)~(37)可得T4端与T1端的光场复振幅之比为
| $ \frac{{{E_{{T_4}}}}}{{{E_{{T_1}}}}} = - \frac{{{{\rm{e}}^{ - {\rm{j}}\omega {t_1}}}\sqrt {\left( {1 - {k_1}} \right)\left( {1 - {k_2}} \right){\rho _C}{\rho _{{L_1}}}} }}{{1 - {{\rm{e}}^{ - {\rm{j}}\omega t}}\sqrt {{k_1}{k_2}{\rho _C}{\rho _L}} }} $ | (38) |
式中t=t1+t2,ρC=ρC1ρC2,ρL=ρL1ρL2。对式(38)左右两边取模的平方,可得T4端与T1端的光功率比
| $ {\left| {\frac{{{E_{{T_4}}}}}{{{E_{{T_1}}}}}} \right|^2} = \frac{{\left( {1 - {k_1}} \right)\left( {1 - {k_2}} \right){\rho _C}{\rho _{{L_1}}}}}{{1 + {k_1}{k_2}{\rho _C}{\rho _L} - 2\sqrt {{k_1}{k_2}{\rho _C}{\rho _L}} \cos \omega t}} $ | (39) |
由式(39)可知,只有满足一定光频率的光才能产生谐振,当T1端入射光频率随时间线性变化时,T4端输出的谐振曲线呈现为暗背景下的亮峰,亮峰处表征光在腔内发生谐振,所以要使得|E4/E1|2取最大值,从而求出光纤谐振环的谐振条件,即cos ωt应取最大值。
综上可知,无论是反射式还是透射式的光纤环形谐振腔,都是在cos ωt取最大值时,光在腔内会出现谐振现象[12]。
当系统相对惯性空间静止时,令cos ω0t0=1,ω0t0取2π的整数倍,即令ω0t0=2qπ,因为ω0=2πν0q,t0=NnL/c,所以
| $ {\nu _{0q}} = \frac{{{\omega _0}}}{{2{\rm{ \mathsf{ π} }}}} = \frac{q}{{{t_0}}} = q \cdot \frac{c}{{NnL}} $ | (40) |
由式(40)可推出
| $ q = \frac{{{\nu _{0q}}nL}}{c} = \frac{{NnL}}{{{\lambda _0}}} $ | (41) |
当系统以角速度Ω相对惯性空间旋转时,式(15)和式(16)分别为顺时针和逆时针光波从M点出发回到M1点所需要的时间tcw和tccw。对于顺时针光波,令cos ωcwtcw=1,ωcwtcw取2π的整数倍,即令ωcwtcw=2qπ,因为ωcwq=2πνcwq,所以
| $ {\nu _{{\rm{cw}}q}} = \frac{{{\omega _{{\rm{cw}}}}}}{{2{\rm{ \mathsf{ π} }}}} = \frac{q}{{{t_{{\rm{cw}}}}}} $ | (42) |
同理,对于逆时针光波,令cos ωccwtccw=1,ωccwtccw取2π的整数倍,即令ωccwtccw=2qπ,因为ωccwq=2πνccwq,所以
| $ {\nu _{{\rm{ccw}}q}} = \frac{{{\omega _{{\rm{ccw}}}}}}{{2{\rm{ \mathsf{ π} }}}} = \frac{q}{{{t_{{\rm{ccw}}}}}} $ | (43) |
可见,对比式(25)、(21)和(22)与式(41)、(42)和(43)发现,无论是采用基于激光物理学中的行波谐振腔理论的方法还是采用基于谐振型光纤陀螺的多光束干涉机理分析的方法,这2种方法所得到的q、νcwq和νccwq均相同,即2种方法所得的谐振频率差Δνq相同。
5 光纤陀螺中的同频相位差与谐振频率差的关系虽然2种形式的光纤陀螺在测量的角速度上的工作机理有所区别,如表 1所示,但是无论是干涉型光纤陀螺还是谐振型光纤陀螺,它们的两路光波时间差Δt是一致的(都是指两路光波从M点到达M1点所需要的时间tcw与tccw的差值)。
|
|
表 1 2种形式的光纤陀螺的工作机理的区别 |
不同的是:干涉型光纤陀螺中,两路光波彼此发生双光束干涉,在相同的频率ν0下进行讨论,并使用同频相位差Δφ来表征系统角速度Ω;谐振型光纤陀螺中,两路光波各自发生多光束干涉,在相同的相移2qπ下进行讨论,并使用谐振频率差Δνq来表征系统角速度Ω。
接下来,讨论两路光波各个物理量之间的关系。设两路光波的初相位相同,根据相移φ等于角频率2πν乘以时间t,即
| $ {\varphi _{{\rm{cw}}}} = 2{\rm{ \mathsf{ π} }}{\nu _{{\rm{cw}}}}{t_{{\rm{cw}}}} $ | (44) |
| $ {\varphi _{{\rm{ccw}}}} = 2{\rm{ \mathsf{ π} }}{\nu _{{\rm{ccw}}}}{t_{{\rm{ccw}}}} $ | (45) |
将式(44)与式(45)相减可得两束光波的相位差为
| $ \Delta \varphi = {\varphi _{{\rm{cw}}}} - {\varphi _{{\rm{ccw}}}} = 2{\rm{ \mathsf{ π} }}\left( {{\nu _{{\rm{cw}}}}{t_{{\rm{cw}}}} - {\nu _{{\rm{ccw}}}}{t_{{\rm{ccw}}}}} \right) $ | (46) |
式(46)可写成微分形式
| $ \Delta \varphi = 2{\rm{ \mathsf{ π} }} \cdot \Delta \left( {\nu t} \right) = 2{\rm{ \mathsf{ π} }} \cdot \left( {{\nu _0}\Delta t + {t_0}\Delta \nu } \right) $ | (47) |
其中Δt=tcw-tccw,Δν=νcw-νccw。对于式(47),无论是干涉型光纤陀螺还是谐振型光纤陀螺都是适用的。
干涉型光纤陀螺中,对于同频相位差Δφ,由于两路光波的频率相同,保持恒定为ν0,故Δν=0。根据式(47)可知,同频相位差Δφ等于角频率2πν0乘以时间差Δt,即
| $ \Delta \varphi = 2{\rm{ \mathsf{ π} }} \cdot \left( {{\nu _0}\Delta t + {t_0}\Delta \nu } \right) = 2{\rm{ \mathsf{ π} }}{\nu _0}\Delta t $ | (48) |
我们可以通过求出两束光波的传输时间差Δt来求得同频相位差Δφ。
谐振型光纤陀螺中,对于谐振频率差Δνq=νccwq-νcwq,虽然陀螺在转动时两束光波的谐振频率νccwq和νcwq不完全相等,但利用谐振条件所得到两束光波纵模模式数都是正整数q,可知两束满足谐振条件的光波在光纤环中所经历的相位都是2qπ。因此谐振相位差Δφq=2qπ-2qπ=0,根据式(47)可知
| $ \Delta \left( {\nu t} \right) = {\nu _0}\Delta t + {t_0}\Delta \nu = 0 $ | (49) |
根据谐振频率差Δνq的定义可知Δν=-Δνq,再由式(49)可得
| $ \Delta {\nu _q} = \frac{{{\nu _0}\Delta t}}{{{t_0}}} $ | (50) |
综合考虑2种形式的光纤陀螺,对比式(48)和(50)可以发现,同频相位差Δφ与谐振频率差Δνq满足如下关系
| $ \Delta \varphi = 2{\rm{ \mathsf{ π} }}{t_0}\Delta {\nu _q} $ | (51) |
由于同频相位差Δφ和静止时光在光纤环中的传播时间t0都与光纤环匝数N成正比,由式(51)可知,因此谐振频率差Δνq与匝数N无关,再次验证了前面的计算结果。
式(51)表明,同频相位差Δφ除以光在光纤环中的传播时间t0恰好等于2π乘以谐振频率差Δνq。
从数学形式上看,式(47)微分式既适用于干涉型光纤陀螺,也适用于谐振型光纤陀螺,是2种陀螺的统一的数学模型。可见相移之差Δφ既与时间之差Δt有关,也与频率之差Δν有关。而无论是哪一种陀螺,时间之差与系统旋转角速度的关系都是一样的,都满足式(18)的关系。因此,从式(47)出发:1)令频率之差Δν为0(两路光波频率都为ν0),即可得出相移之差(同频相位差Δφ),即为干涉型光纤陀螺的待测物理量;2)令相移之差Δφq为0(两路光波相移都为2qπ),即可得出频率之差(谐振频率差Δνq),即为谐振型光纤陀螺的待测物理量。而式(51)则是综合考虑2种光纤陀螺的待测物理量建立的关系,即式(51)中的同频相位差Δφ和谐振频率差Δνq,只要已知其中一个参数,就可以利用此式得出另一个参数。
从物理意义上看,Sagnac效应敏感环形光路通过测量顺逆时针光的传输差异,从而测出系统旋转的角速度。然而,实际检测中时间差或光程差这种差异往往极小不易观测,因此需要通过其他物理量之差(相移之差或频率之差)来测量:干涉型光纤陀螺利用顺逆时针光频率相同,测出相移之差(同频相位差Δφ);而谐振型光纤陀螺利用顺逆时针光相移相同,测出频率之差(谐振频率差Δνq)。而式(51)包含了3个物理量:传输时间t0、同频相位差Δφ、谐振频率差Δνq。式(51)体现了2种陀螺顺逆时针光的传输差异,是2种陀螺物理量关系的有机统一,这3个物理量有以下几点特点。
1) 与光纤环匝数N的关系:传输时间t0和同频相位差Δφ都与光纤环匝数N成正比,因此由式(51)可得出谐振频率差Δνq与光纤环匝数N无关的结论,再次验证了前面谐振频率差Δνq的计算结果。
2) 与有效折射率n的关系:传输时间t0与有效折射率n成正比,而谐振频率差Δνq与有效折射率n成反比,因此由式(51)也可得出同频相位差Δφ与有效折射率n无关的结论,再次验证了前面同频相位差Δφ的计算结果。
3) 与环的长度L和面积S的关系:传输时间t0与环的长度L成正比,而同频相位差Δφ与环的面积S成正比,因此由式(51)也可得出谐振频率差Δνq与S成正比且与L成反比。
4) 与光波长λ0的关系:同频相位差Δφ和谐振频率差Δνq都与光波长λ0成反比,而传输时间t0与光波长λ0无关,这一点在式(51)中也能得以体现。
5) 与系统角速度Ω的关系:同频相位差Δφ和谐振频率差Δνq都与系统角速度Ω成正比,而传输时间t0与系统角速度Ω无关,这一点在式(51)中也能得以体现。
综上可知,式(51)可以作为物理量之间的关系即前面计算结果的验证手段。如果将2种陀螺放在同一个系统对旋转角速度Ω进行检测,由于同频相位差Δφ和谐振频率差Δνq都与系统角速度Ω成正比,因此当整个系统相对于惯性空间旋转的角速度增大时,由式(51)可见,干涉型光纤陀螺同频相位差Δφ和谐振型光纤陀螺谐振频率差Δνq这两个物理量都会同步增大,这2个物理量都能同时体现整个系统旋转的快慢程度。
6 结论1) 对于这2种干涉型光纤陀螺,本文采用了以惯性空间为参考系的路程叠加法证明了Sagnac效应是一种与介质无关的纯空间延迟,有效折射率n对Sagnac时间差Δt和光程差Δδ均没有影响。2)对于干涉型光纤陀螺,有效折射率n对Sagnac相移差Δφ也没有影响。3)对于谐振型光纤陀螺,本文提出了2种方法,即基于激光物理学中的行波谐振腔理论和基于多光束干涉机理,求出谐振环形腔的谐振频率差Δνq的表达式。4)得出光纤陀螺中的相位差Δφ和的谐振频率差Δνq之间所满足的关系,并分别从数学形式和物理意义上对这一关系作出分析。2种陀螺的光路结构虽不同,但可使用统一的模型表达及分析光学物理量之间的关系。
| [1] |
杨亭鹏, 刘星桥, 陈家斌. 光纤陀螺仪(FOG)技术及发展应用[J]. 火力与指挥控制, 2004, 29(2): 76-79. DOI:10.3969/j.issn.1002-0640.2004.02.022 ( 0) 0)
|
| [2] |
周海波, 刘建业, 赖际舟, 等. 光纤陀螺仪的发展现状[J]. 传感器技术, 2005, 24(6): 1-3. DOI:10.3969/j.issn.1000-9787.2005.06.001 ( 0) 0)
|
| [3] |
JIN Jing, LIU Jixun, HUANG Yunlong, et al. A reliable and efficient method for temperature sensing in interferometric fiber-optic gyro[J]. IEEE sensors journal, 2016, 16(11): 4192-4197. DOI:10.1109/JSEN.2016.2542280 ( 0) 0)
|
| [4] |
BACURAU R M, SPENGLER A W, DANTE A, et al. Technique for suppressing the electronic offset drift of interferometric open-loop fiber optic gyroscopes[J]. Optics letters, 2016, 41(22): 5186-5189. DOI:10.1364/OL.41.005186 ( 0) 0)
|
| [5] |
JIAO Hongchen, FENG Lishuang, WANG Junjie, et al. Transmissive single-beam-splitter resonator optic gyro based on a hollow-core photonic-crystal fiber[J]. Optics letters, 2017, 42(15): 3016-3019. DOI:10.1364/OL.42.003016 ( 0) 0)
|
| [6] |
XU Zhenlong, LI Xuyou, ZHANG Chunmei, et al. Design of single-polarization coupler based on dual-core photonic band-gap fiber implied in resonant fiber optic gyro[J]. Optics communications, 2016, 380: 302-309. DOI:10.1016/j.optcom.2016.06.005 ( 0) 0)
|
| [7] |
YING Diqing, MAO Jianmin, LI Qiang, et al. A miniaturized compact open-loop RFOG with demodulation signal compensation technique to suppress intensity modulation noise[J]. Optics communications, 2016, 359: 364-371. DOI:10.1016/j.optcom.2015.10.006 ( 0) 0)
|
| [8] |
WANG Linglan, LI Hanzhao, ZHANG Jianjie, et al. Optimization of the sinusoidal phase modulation technique in resonant fiber optic gyro[J]. Optics communications, 2017, 387: 18-23. DOI:10.1016/j.optcom.2016.11.025 ( 0) 0)
|
| [9] |
YING Diqing, WANG Zeyu, MAO Jianmin, et al. An open-loop RFOG based on harmonic division technique to suppress LD's intensity modulation noise[J]. Optics communications, 2016, 378: 10-15. DOI:10.1016/j.optcom.2016.05.056 ( 0) 0)
|
| [10] |
张桂才. 光纤陀螺原理与技术[M]. 北京: 国防工业出版社, 2008: 30-34.
( 0) 0)
|
| [11] |
王巍. 光纤陀螺惯性系统[M]. 北京: 中国宇航出版社, 2010: 35-37.
( 0) 0)
|
| [12] |
张维叙. 光纤陀螺及其应用[M]. 北京: 国防工业出版社, 2008: 16-19.
( 0) 0)
|
| [13] |
章燕申, 伍晓明. 光学陀螺系统与关键器件[M]. 北京: 中国宇航出版社, 2010: 188-189.
( 0) 0)
|
| [14] |
YING Diqing, YE Kebin, WANG Zeyu, et al. Optimization of second-harmonic's quantization precision for intensity modulation noise suppressing in a digital RFOG[J]. Optics communications, 2017, 405: 114-119. DOI:10.1016/j.optcom.2017.07.071 ( 0) 0)
|
| [15] |
毛骏健, 顾牡. 大学物理学下册[M]. 2版. 北京: 高等教育出版社, 2013: 143.
( 0) 0)
|
| [16] |
WALKER J S. Physics[M]. 3rd ed. Pearson Education, 2007: 981.
( 0) 0)
|
| [17] |
EINSTEIN A, LAWSON R W, PENROSE R, et al. Relativity:the special and general theory[M]. New York: The Masterpiece Science Edition, 2005: 53.
( 0) 0)
|
| [18] |
NARLIKAR J V. An introduction to relativity[M]. New York: Cambridge University Press, 2010: 11.
( 0) 0)
|
| [19] |
王巍. 干涉型光纤陀螺仪技术[M]. 北京: 中国宇航出版社, 2010: 20-21.
( 0) 0)
|
| [20] |
崔忠升. 数字谐振式光纤陀螺的理论和实验研究[D]. 杭州: 浙江大学, 2004: 12. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y581085
( 0) 0)
|
| [21] |
李强. 谐振式光纤陀螺小型化技术研究[D]. 杭州: 浙江大学, 2015: 10. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2978878
( 0) 0)
|
| [22] |
卢霄. 双路闭环谐振式光纤陀螺数字信号检测系统的设计与实现[D]. 杭州: 浙江大学, 2014: 9. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014162846.htm
( 0) 0)
|
| [23] |
UDD E. Introduction to "Fiber optic gyros: 10th anniversary conference"[C]//Proceedings Volume 0719, Fiber Optic Gyros: 10th Anniversary Conf. Cambridge, MA, United States: SPIE, 1987: 3. http://spie.org/Publications/Proceedings/Paper/10.1117/12.937530
( 0) 0)
|
| [24] |
李景振. 谐振式型光纤陀螺的设计与研制[D]. 深圳: 深圳大学, 2014: 9.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


