2. 航空机电综合航空科技重点实验室 电子工程部, 江苏 南京 211106
2. Electronic Engineering Department, Aviation Key Laboratory of Science And Technology on Aero Electromechanical System Integration, Nanjing 211106, China
液压作动筒是液压伺服系统中的执行部分,将输入的液压能转变为机械能的能量转换装置,是做直线往复运行或摆动运动的液压执行元件。液压作动筒的故障将直接影响系统的健康状态,所以需要对作动筒进行有效地故障诊断。目前,作动筒泄漏等故障检测的方法主要是根据进油路和回油路的流量传感器和压力传感器通过参量的变化来诊断故障[1]。而传统的传递函数建模法难以得到流量数据且不易进行故障注入,为作动筒的故障诊断方法的研究造成困难[2]。在故障诊断方面,主要分为基于模型的方法和数据驱动的方法[3]。其中,基于模型的方法主要分为基于观测器法和基于系统辨识的诊断方法,但是随着工业系统复杂化的提高,很难依靠传统的方法对整个工艺流程建立精确的模型。相反,随着工业数据的持续积累、机器学习算法的发展,基于数据驱动的方法和多种方法混合的故障识别已成为近年来的研究热点[4]。
本文首先提出一种以AMESim软件为设计平台,对作动筒位置控制系统进行建模和故障注入的方法,并通过分析作动筒的参数曲线,验证此建模方法的正确性。然后,结合小波包分解的时频特性和支持向量机在小样本情况下的模式识别能力及良好的泛化能力,对作动筒进行故障诊断,一定程度上避免了单一分类方法的局限性,提高了分类能力。
1 阀控作动筒位置控制系统建模 1.1 AMESim软件AMESim是在20世纪90年代法国Imagine公司推出的专门针对机械方面的系统建模、仿真和动力学分析的软件[5]。AMESim主要包括模型搭建、元件库构建、仿真分析等功能模块,组成了一个完整的开发环境。同时基于物理模型的图形化的开发方式、智能化的求解器和数量巨大的元件库,使得用户可以通过在完整的应用库中选择需要的模块来构造复杂系统的模型,为用户带来了极大的方便,减少了开发成本,缩短了研发时间[6]。
针对液压系统的仿真,在AMESim中最常用的库有:标准液压库、液阻库和液压元件设计库。
1.2 阀控作动筒位置控制系统建模过程阀控作动筒位置控制系统主要由伺服放大器、伺服阀、作动筒和位置传感器4部分组成[7]。利用AMESim对液压系统进行建模仿真,需要完成以下4个阶段:
1) 草图模式:在该阶段中,主要是从不同的应用库中选取或设计仿真元件,并有机地连接在一起,形成自己的仿真模型。
2) 子模型模式:为每个元件选取数学模型,建立仿真模型之间的联系。往往一个元件对应多个子模型,设计中常采用各元件的Primal Mode。
3) 参数模式:为每个仿真元件设置参数。参数的设定决定了最终建立的仿真模型与实际系统的相似度。
4) 运行模式:运行仿真,分析并绘出仿真结果。
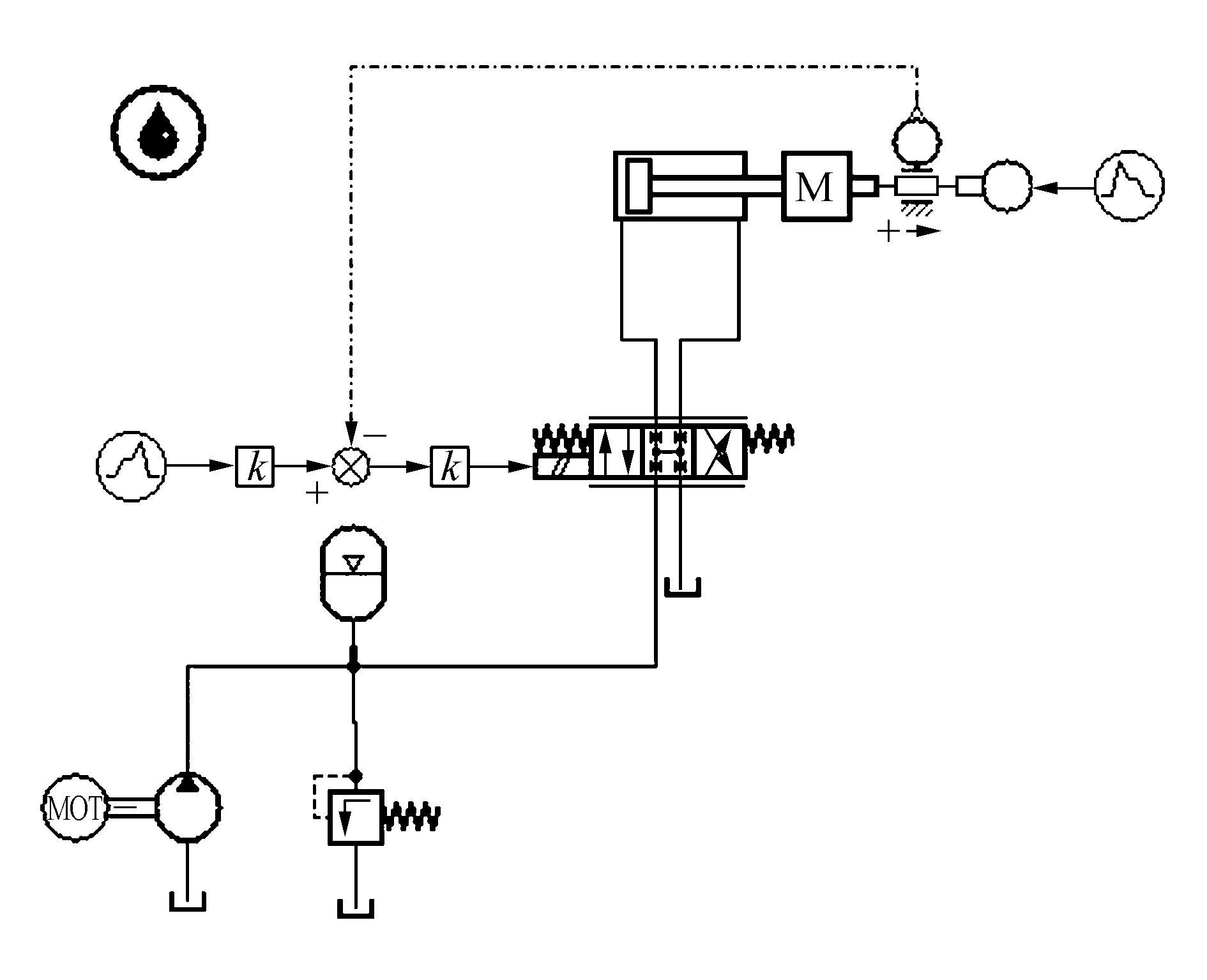
在AMESim中利用机械库、液压库、信号源等模块搭建作动筒位置控制系统模型,如图 1所示。
|
Download:
|
| 图 1 作动筒位置控制系统的仿真模型 | |
为搭建好的系统各元件子模型选择系统提供的优先子模型,接着为每个组件设置参数。主要子模型的参数设置如表 1所示。
|
|
表 1 作动筒位置控制系统元件参数 |
针对图 1建立的模型,通过在参数模式下改变作动筒的参数值,人为地设置作动筒泄露、负载外力突增、活塞杆轴心偏移3种故障模式。AMESim软件中的参数设置项和故障模式的对应关系如表 2所示。
|
|
表 2 AMESim模型参数和故障模式对应表 |
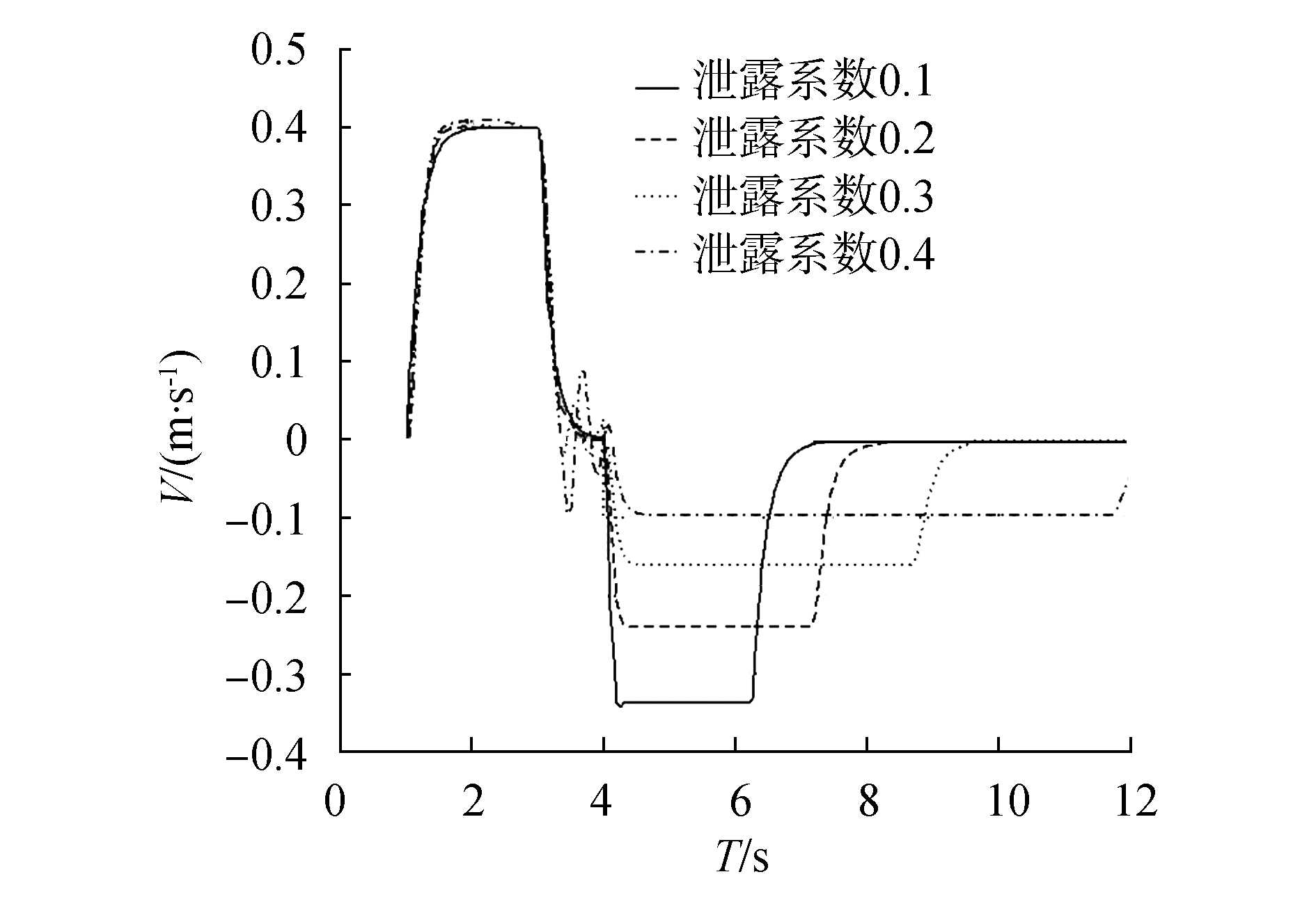
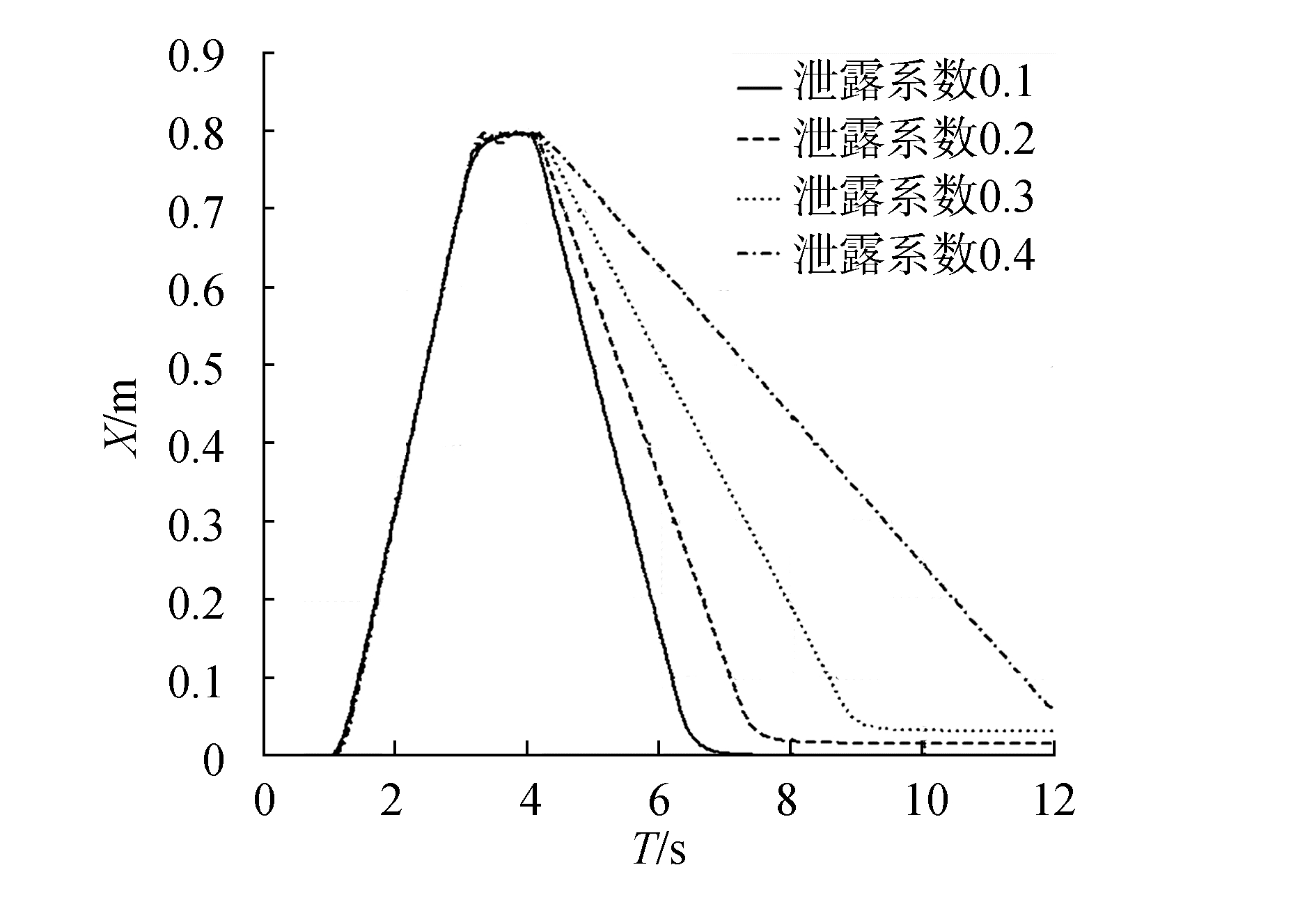
以泄露故障为例进行分析,设置4种程度泄露故障(泄露系数分别为0.1、0.2、0.3、0.4),从而验证模型建立的正确性。本文设计的作动筒,初始状态为活塞杆未伸出,当无杆腔中通入高压油后,活塞杆逐渐变为完全伸出状态,然后保持一小段时间后,再由伸出状态缩回到初始状态。当有杆腔出现泄漏故障时,活塞杆从伸出到初始状态的过程中,速度明显下降;相应地,活塞杆回到初始态的时间延长,且由于油液的泄露,作动筒活塞杆甚至出现难以回到最初状态的现象。从图 2的速度曲线和图 3的位移曲线可以清楚地看出以上现象。
|
Download:
|
| 图 2 泄露故障条件下活塞杆速度曲线 | |
|
Download:
|
| 图 3 泄露故障条件下活塞杆位移曲线 | |
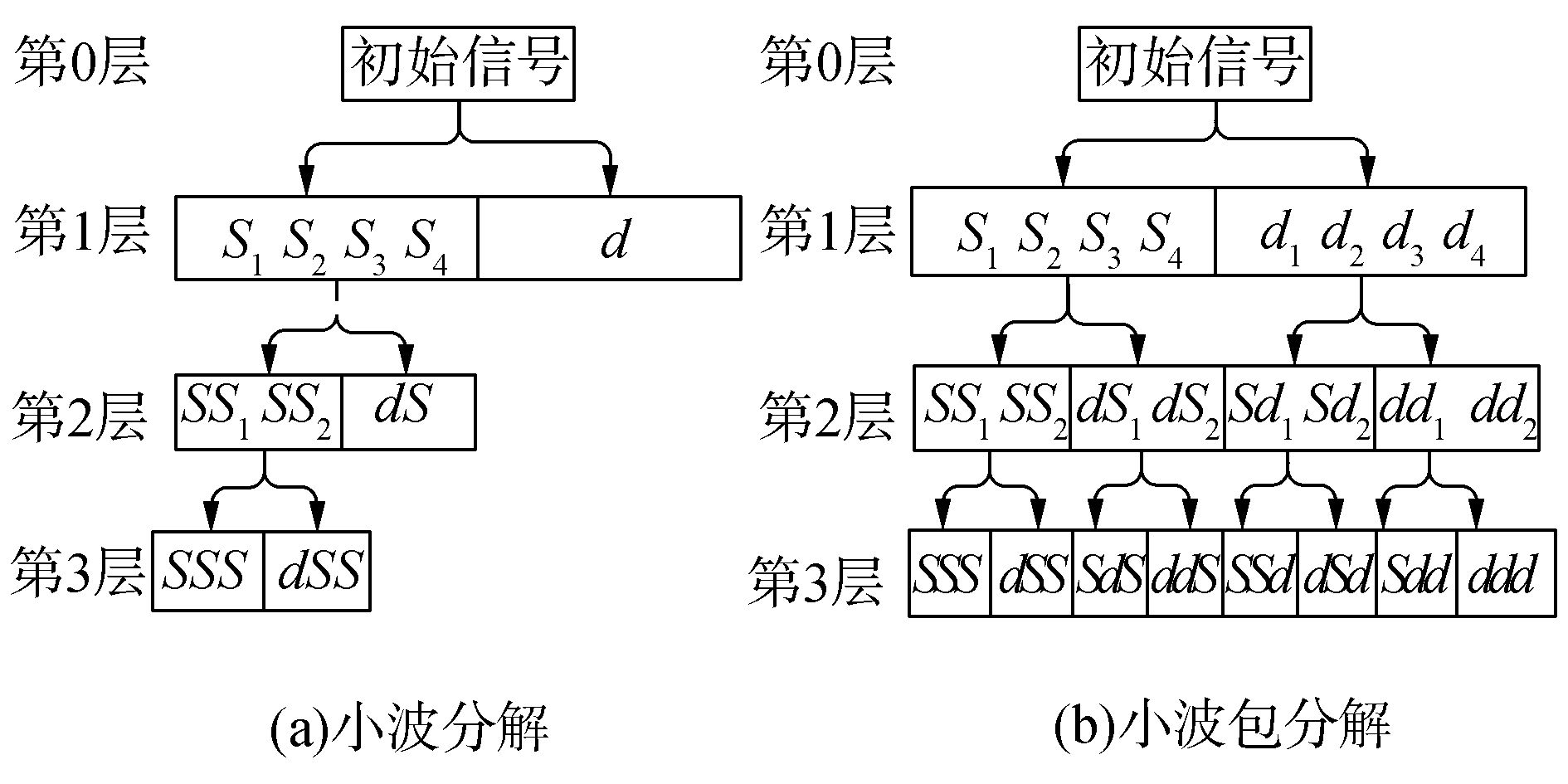
小波分析[8]是一种时频域的分析方法,采用多尺度细化措施对非平稳信号分析,达到高频处时间细分和低频处频率细分的效果,能自适应时频分析的要求从而聚焦到信号的任意细节。其基本思想是用小波函数系去表示或者逼近信号或函数,而小波函数系是经过基本小波的变换即平移和伸缩构成的。小波包是为了克服小波变换对频带不均匀划分的特性,避免了小波变换高频频带宽和低频频带窄的特点。它是一种更精细的信号分析的方法,提高了信号的时域分辨率[9]。两者分解比较示意如图 4所示。
|
Download:
|
| 图 4 小波分解和小波包分解比较示意 | |
基于小波包分解提取多尺度空间能量特征的原理是把不同分解尺度上的信号能量求解出来,将这些能量值按尺度顺序排列成特征向量供识别使用[10]。下面给出小波包能量算子E(j, i)的定义。
定义:对于某一给定的正交小波包空间,原始信号s(t)在该时频局域化空间的能量分布E(j, i)定义如下[11]:
| $ E\left( {j, i} \right) = \mathop \sum \limits_{k \in Z} {\left[ {{p_s}\left( {n, j, k} \right)} \right]^2} $ |
式中:E(j, i)表示在分解层次j上第i个结点的能量值;ps(n, j, k)是小波包变换系数,可以采用类似于Mallat快速小波分解算法得到[12]。实际应用中,往往对各结点能量归一化即取各节点能量所占的百分比。
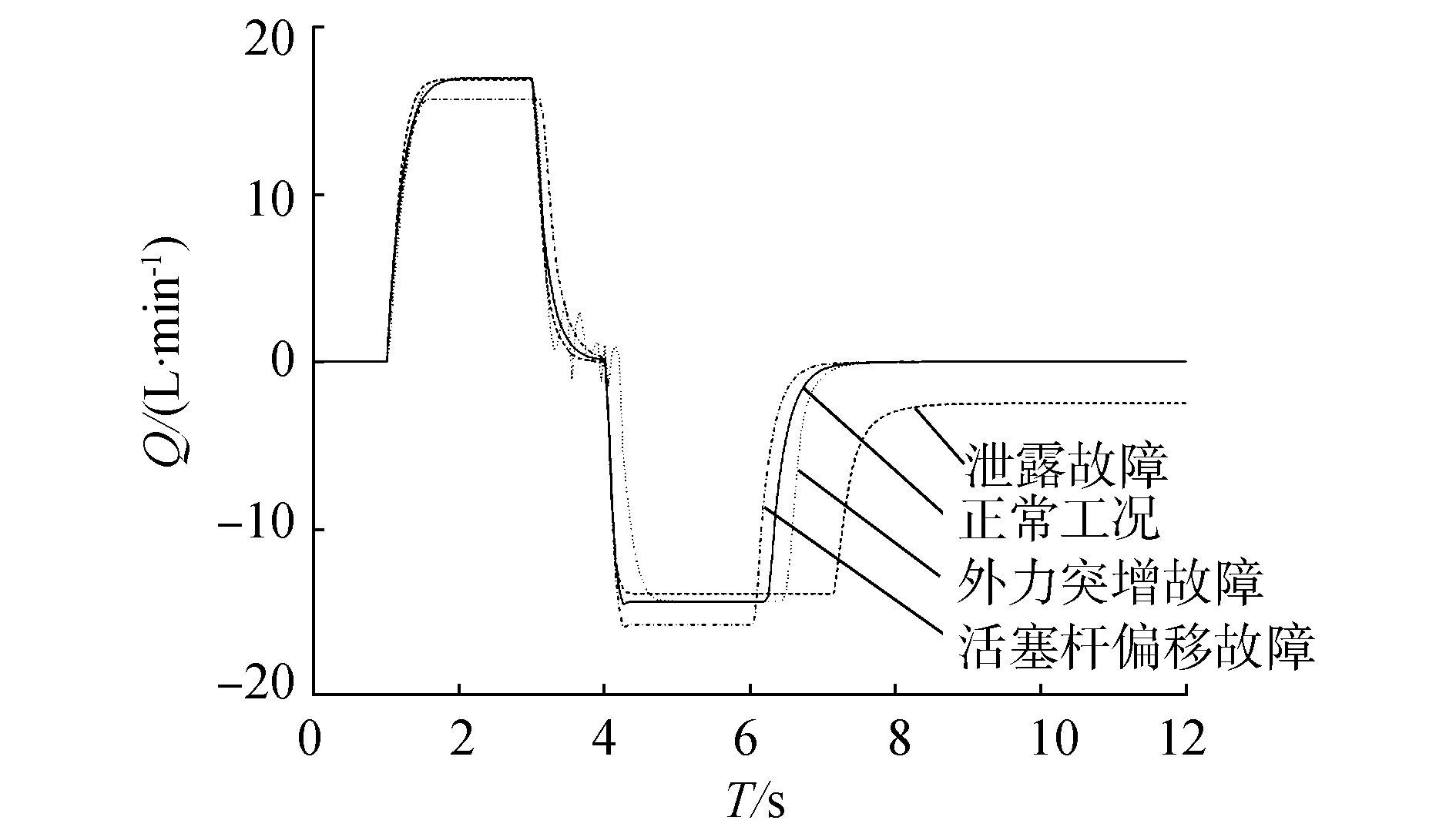
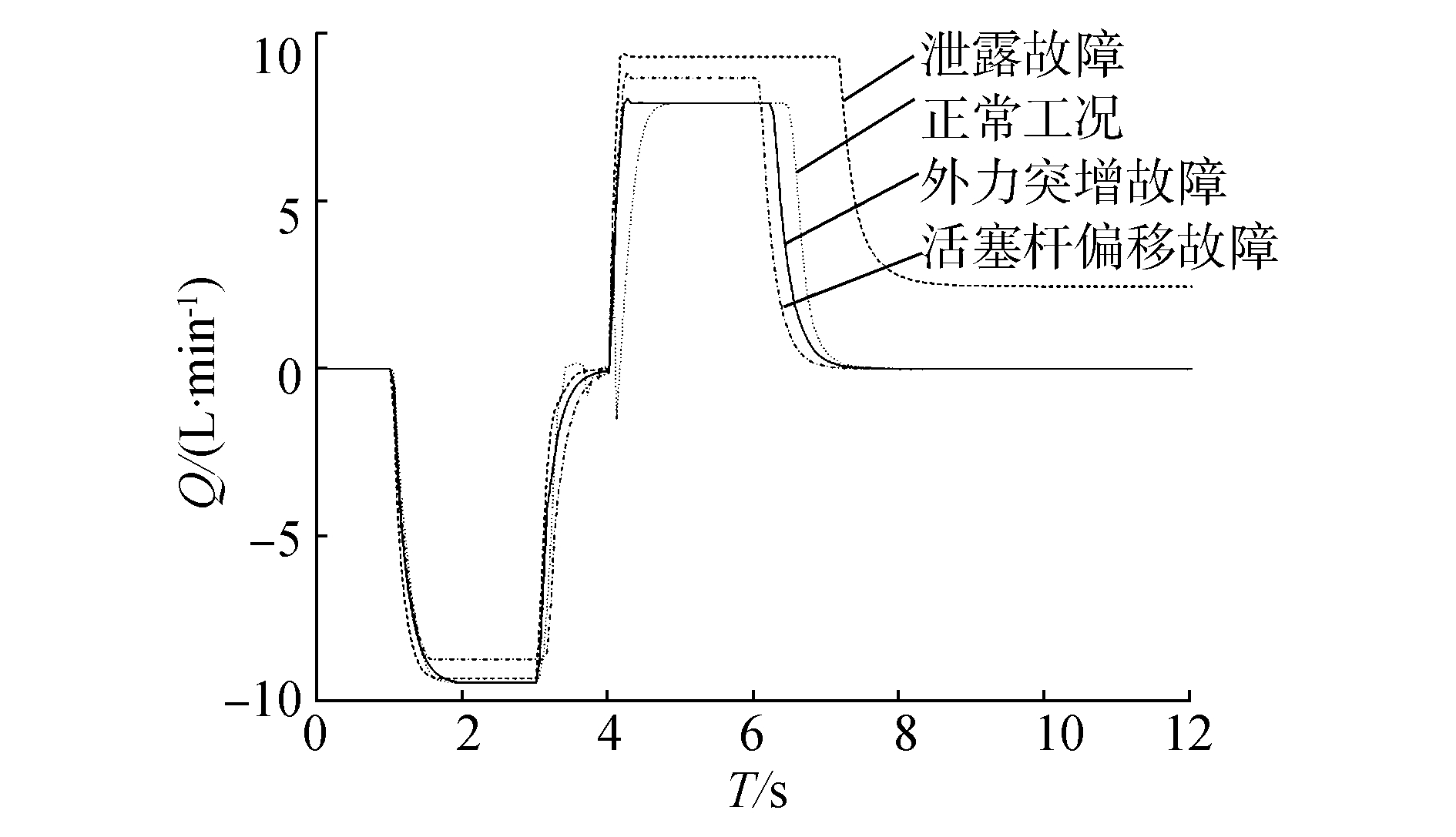
2.2 基于小波包能量的特征提取针对作动筒的不同工况,从作动筒两腔流量曲线图 5、6中看出,作动筒4种工况下有杆腔和无杆腔流量具有不同的流量脉动且在局部有一跳跃,经小波包分解后信号被分解到各个频段,各频段所包含的能量频谱分布与作动筒工作状况密切相关,因此可用于识别分类。
|
Download:
|
| 图 5 不同工况下作动筒无杆腔流量 | |
|
Download:
|
| 图 6 不同工况下作动筒有杆腔流量 | |
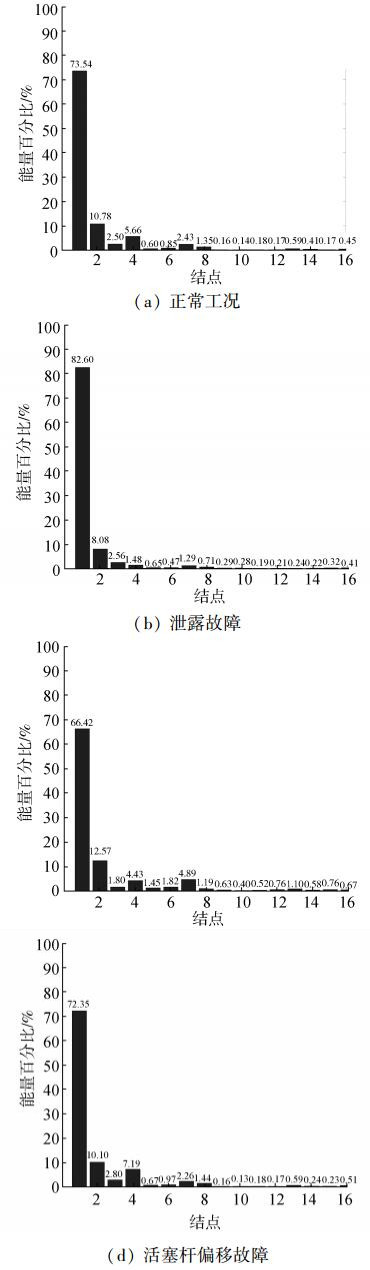
本文根据AMESim故障注入得到的数据,以0.05 s为步长,对每组数据进行离散小波包分解,采用db5小波函数,进行4层小波包分解,得到每组数据的第4层能量分布直方图,图 7中给出4种工作模式下其中一组样本的能量分布。
|
Download:
|
| 图 7 无杆腔流量能量分布直方图 | |
从图 7可以看出,各工作模式下,能量主要集中在第4层小波包分解后的前4个结点,因此本文选取前4个结点能量作为特征值,即特征向量T为
| $ \mathit{\boldsymbol{T}} = \left[ {{E_1}, {E_2}, {E_3}, {E_4}, {E_5}, {E_6}, {E_7}, {E_8}} \right] $ |
式中:E1、E2、E3、E4为无杆腔流量第4层小波包分解后的前4个结点的能量百分比,E5、E6、E7、E8为有杆腔流量第4层小波包分解后的前4个结点的能量百分比。
文中16个尺度空间中选取4个能量相对集中的尺度空间组成特征向量,既能充分利用原始信息,又能减小特征维数,加快分类速度。
3 阀控作动筒位置控制系统故障诊断 3.1 支持向量机支持向量机[13]是在1995年由Cortes和Vapnik第一次提出,建立在统计学习理论中的VC维理论和结构风险最小原理基础上的,能够根据有限的样本信息,在模型的复杂度和学习能力之间寻求最佳折衷,以期获得良好的泛化能力。SVM在解决小样本、非线性及高维模式识别问题中表现优良。这些特点也使支持向量机方法特别适合于故障诊断这种小样本的情况。
对于一个给定的线性可分数据集
| $ \left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_l}, {y_l}} \right), x \in {R^d}, y \in \left\{ { + 1, - 1} \right\} $ |
可以被一个超平面
| $ \mathit{\boldsymbol{\omega }} \cdot x + b = 0 $ |
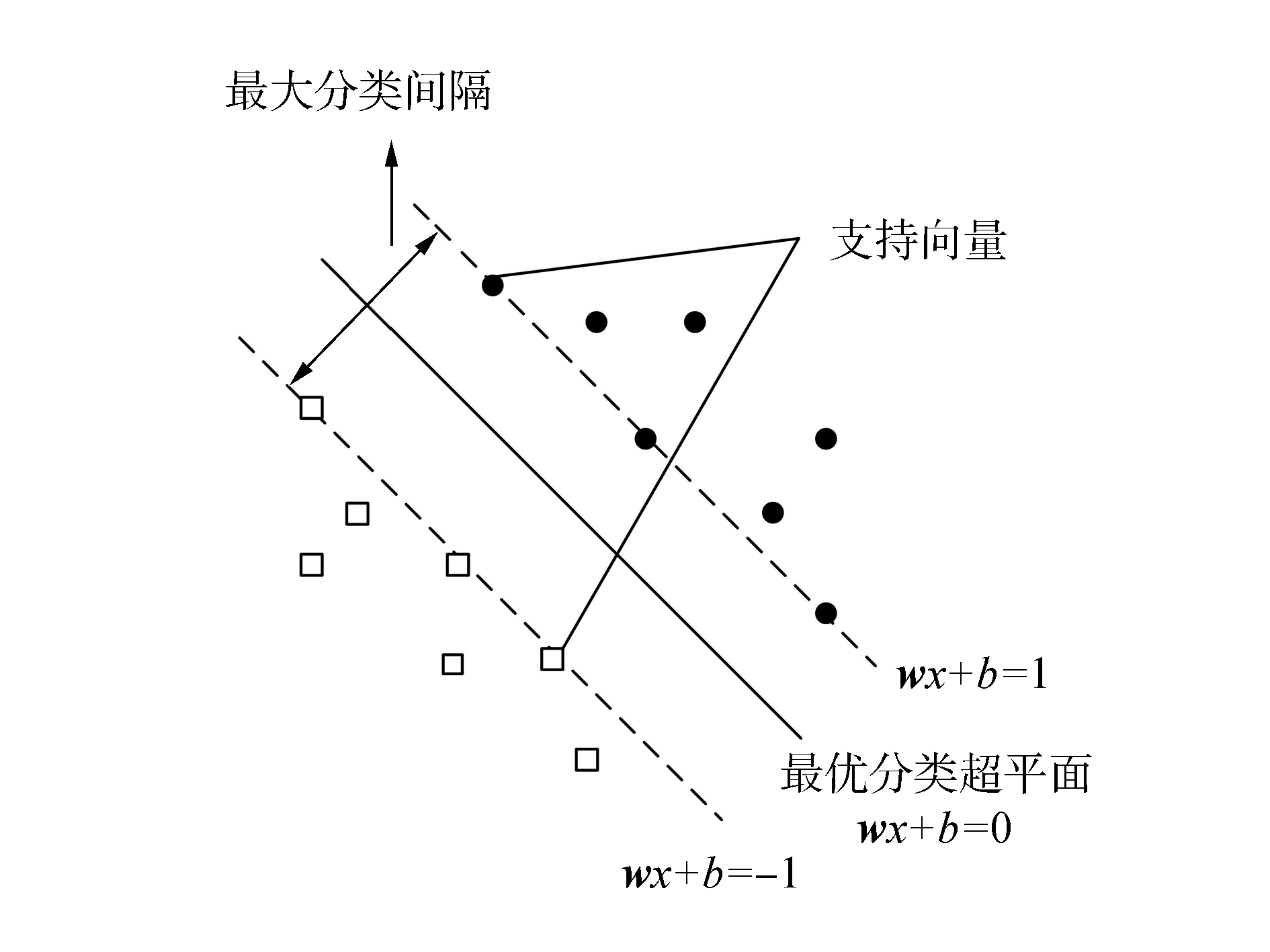
分开,如果所有的数据样本均被超平面没有错误地分开且离超平面最近的向量与超平面之间的距离是最大的,那么就称这个超平面为最优超平面。如图 8所示。
|
Download:
|
| 图 8 最优分类超平面 | |
经过一系列整理和优化[13],上述最优分类面问题可以表示成如下的约束优化问题,即
| $ \begin{array}{*{20}{c}} {{{\min }_{\omega , b}}\frac{1}{2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{y_i}({\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i} + b) \ge 1, i = 1, 2, \cdots , l} \end{array} $ |
为了解决样本的线性不可分问题,通过将低维数据映射到高维特征空间,然后在高维的特征空间中构造出需要的最优分类超平面。为此,引入核函数概念,达到数据映射效果且解决高维数据计算量大的问题。
实际上,上面的方法可以称做“硬间隔”分类法,其硬性地要求每一个样本点都必须满足以下条件:样本点与分类平面间的距离大于某个固定值。但在实际应用中,总是会存在一些“离群点”,因此需要引入容错性,即在约束条件中引入松弛变量,这时,最优分类面问题可以演化为[14]:
| $ \begin{array}{*{20}{c}} {\min \frac{1}{2}||\mathit{\boldsymbol{\omega }}|{|^2} + C\sum\limits_{i = 1}^l {{\zeta _i}} }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{y_i}({\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i} + b) \ge 1 - {\zeta _i}}\\ {i = 1, 2, \cdots , l}\\ {{\zeta _i} \ge 0} \end{array} $ |
式中:参数C是一个需要提前给定的常数,它表示对错分样本的惩罚程度,实现最少错分样本和最大分类间隔之间的折中。显然C过大,目标函数越大,趋向于无解。综上所述,影响SVM分类器性能的关键参数为惩罚参数C和核函数参数。
3.2 基于支持向量机的故障诊断从图 7可以得到表 3的数据,从中可以看出,虽然经过小波包分解后的结点能量可以作为故障诊断的特征值,并且可以初步分类,但是仍存在不是很明显的界限比如正常工况和活塞杆偏移故障之间。因此,进一步采用SVM进行分类,提高分类准确率。
|
|
表 3 无杆腔流量能量值 |
基于支持向量机的故障诊断方法的具体步骤如下:
1) 故障注入:采用AMESim软件的批处理功能可以对同一个参数同时设置不同值,可以一次性获取同一模式的多组流量信息。本文对正常工况、泄露故障、外力突增故障和活塞杆轴心偏移4种模式各获取19组数据。
2) 提取特征向量:分别对液压作动筒的正常工况、泄露故障、外力突增故障和活塞杆轴心偏移故障4种模式进行基于小波包能量的特征提取,共得到76组特征向量,对应4种工作模式。
3) SVM分类:选用LibSVM软件包[15]在MATLAB环境下搭建作动筒故障诊断平台。将特征向量作为SVM的输入数据,采取网格参数寻优的方法对惩罚参数C和RBF核函数参数γ进行选择,随机选取64组数据作为训练集,其余12组做为测试集,共进行3次实验,采用混淆矩阵和整体准确率评估模型的准确性,实验结果如表 4所示。
|
|
表 4 SVM分类结果 |
由表 4可知,通过SVM训练得到的模型对包含12组数据的测试集的分类准确率达到90%以上,取得比较好的诊断效果并且具有较快的运行速度。
4 结论1) 利用AMESim仿真软件建立了液压作动筒的故障仿真模型,得出了位置控制系统中作动筒的流量曲线,解决了传统的传递函数仿真法故障注入难的问题,为故障检测及诊断提供了方法性的指导。
2) 采用的小波包分解及能量谱的特征提取方法,有效地获取了流量脉动曲线中的信息,并与支持向量机方法相结合进行故障诊断,取得了比较高的识别率且具有比较短的运行时间。
本文展示的故障诊断方法可以推广到很多研究领域,具有一定的指导意义。但是,本文仅仅对单一故障部件进行诊断,并没有考虑多种故障同时发生的状况,今后将做进一步的探索。
| [1] |
刘兵. 工程机械中液压缸故障诊断及维修方法探讨[J]. 科学与财富, 2013(11): 178. DOI:10.3969/j.issn.1671-2226.2013.11.146 ( 0) 0)
|
| [2] |
强保民, 刘保杰. 阀控非对称液压缸建模方法研究[J]. 装备制造技术, 2011(3): 9-12. DOI:10.3969/j.issn.1672-545X.2011.03.004 ( 0) 0)
|
| [3] |
李向前. 复杂装备故障预测与健康管理关键技术研究[D]. 北京: 北京理工大学, 2014: 4-7. http://cdmd.cnki.com.cn/Article/CDMD-10007-1014086745.htm
( 0) 0)
|
| [4] |
王少萍. 液压系统故障诊断与健康管理技术[M]. 北京: 机械工业出版社, 2014: 16-18.
( 0) 0)
|
| [5] |
梁全, 苏齐莹. 液压系统AMESim计算机仿真指南[M]. 北京: 机械工业出版社, 2014: 1-26.
( 0) 0)
|
| [6] |
余佑官, 龚国芳, 胡国良. AMESim仿真技术及其在液压系统中的应用[C]//2012年LMS中国用户大会论文集. 桂林, 2012. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=YYQD200503008&dbname=CJFD&dbcode=CJFQ
( 0) 0)
|
| [7] |
徐保强, 吴勇, 王颖, 等. 基于AMESim的液压缸位置控制系统的建模与仿真[J]. 煤矿机械, 2015, 36(12): 113-115. ( 0) 0)
|
| [8] |
李刚, 许鹏程, 韩龙美. 基于小波分析的电力系统故障时空检测与诊断[J]. 系统仿真学报, 2015, 27(12): 3018-3024. ( 0) 0)
|
| [9] |
单亚峰, 孙璐, 付华, 等. 基于小波包和RBF神经网络的瓦斯传感器故障诊断[J]. 传感技术学报, 2015, 28(2): 278-283. DOI:10.3969/j.issn.1004-1699.2015.02.023 ( 0) 0)
|
| [10] |
石明江, 罗仁泽, 付元华. 小波和能量特征提取的旋转机械故障诊断方法[J]. 电子测量与仪器学报, 2015, 29(8): 1114-1120. ( 0) 0)
|
| [11] |
李世玲, 李治, 李合生. 基于小波包能量特征的滚动轴承故障监测方法[J]. 系统仿真学报, 2003, 15(1): 76-80, 83. DOI:10.3969/j.issn.1004-731X.2003.01.021 ( 0) 0)
|
| [12] |
王明祥, 宁宇蓉, 王晋国. 基于Mallat算法的一维离散小波变换的实现[J]. 西北大学学报:自然科学版, 2006, 36(3): 364-368. ( 0) 0)
|
| [13] |
张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32-42. DOI:10.3969/j.issn.1003-8930.2000.01.008 ( 0) 0)
|
| [14] |
焦卫东, 林树森. 整体改进的基于支持向量机的故障诊断方法[J]. 仪器仪表学报, 2015, 36(8): 1861-1870. DOI:10.3969/j.issn.0254-3087.2015.08.023 ( 0) 0)
|
| [15] |
CHANG C C, LIN C J. LIBSVM: a library for support vector machines. [2011-10-07]. http://www.csie.ntu.edu.tw/~cjlin/libsvm/.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


