2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
海上航运过程中,船舶遭遇恶劣海况、搁浅、触底、碰撞等灾难情况时有发生,如“加百利”号轮船发生的海难[1]、“协和”号游轮在意大利的搁浅[2],给船东、船厂带来巨大经济和名誉损失,所以说在设计的初期阶段对船舶的破舱稳性进行评估可以最大程度降低发生海难的后果。
破舱稳性的研究主要分为确定性方法和概率性方法[3]。概率破损稳性最早是德国的Kurt Wendel教授于20世纪60年代提出的[4]。前苏联学者马涅采夫[5]提出将船舶不沉概率作为统一的不沉性指标,开启了概率性计算的新篇章,随着计算机技术和人们认知的不断加深,概率性方法已经开始取代确定性方法用来计算破损稳性[6]。IMO概率性方法施行在1992年后建造的干货船上,这就是SOLAS 1992[7]。随后国际海事组织海上安全委员会(IMO)将SOLAS 1990和SOLAS 1992进行统一,并在2009年强制施行[8],从此人们开始重视其研究。大连理工大学的王侨[9]对新旧SOLAS公约进行对比。黄武刚[10]利用FORAN进行了破舱稳性的研究。周晓明[11]借助VBA和Active X对船舶分舱和破舱稳性进行研究。其他学者也研究了客滚船的破舱稳性 [12]。
本文将以SOLAS 2009为理论依托,研究概率破舱稳性的计算原理以及评估方法。理解区域破损的理念,采用maxsurf软件为辅助工具,进行实船的破舱稳性计算,分析SOLAS 2009的计算规律,评估分舱的合理性,对不合理的舱室进行优化。
1 SOLAS 2009公约SOLAS 2009中采用了概率评估的方法来衡量船舶的破舱稳性是否达到要求,主要含有参数
对于船长(
| $R = 1 - \frac{{128}}{{{L_S} + 152}}$ |
对船长
| $R = 1 - \frac{1}{{1 + \displaystyle\frac{{{L_S}}}{{100}} \times \displaystyle\frac{{{R_0}}}{{1 - {R_0}}}}}$ |
式中
| $A = 0.4{A_s} + 0.4{A_p} + 0.2{A_l}$ |
| $AC = \sum\limits_{}^{} {P_i \cdot S_i \cdot V_i} $ |
式中:
对船舶进行概率破舱稳性计算的首要任务为划分破损区域,其中包括纵向、横向、垂向区域的划分,依据公约规定利用水密舱壁进行区域划分。
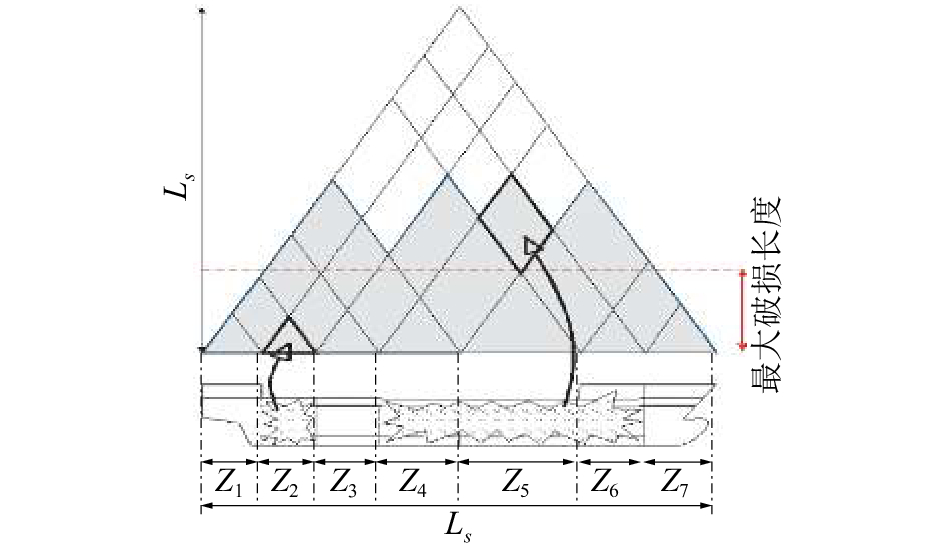
2.1 纵向区域划分划分一般从船艉开始向船艏方向划分,船舶纵向区域的位置和长度将直接影响它的浸水概率。划分完纵向位置后,可得到概念框架图如图 1所示。
|
Download:
|
| 图 1 概念框架 | |
图 1中横纵坐标为船舶的分舱长度,底部的三角形代表对应船舶的该区域舱室破损,第2层的四边形代表其下的两个相邻区域同时破损。以此类推,第3层为相邻的3个区域同时破损。但公约内破损区域的长度并不是无限的(过长的区域破损计算时其残存概率为0,对达到的分舱指数
计算破损概率
标准化最大破损总长:
| ${J_{\max }} = 10/33$ |
折角点分布:
| ${J_{kn}} = 5/33$ |
在
| ${p_k} = 11/12$ |
最大绝对破损长度:
| ${l_{\max }} = 60 \;{\rm{m}}$ |
标准化分布短点长度:
| ${L^*} = 260 \;{\rm{m}}$ |
| ${b_0} = 2\left( {\frac{{{p_k}}}{{{J_{kn}}}} - \frac{{1 - {p_k}}}{{{J_{\max }} - {J_{kn}}}}} \right)$ |
当
| ${J_m} = \min \left\{ {{J_{\max }},\frac{{{l_{\max }}}}{{{L_s}}}} \right\}$ |
| ${J_k} = \frac{{{J_m}}}{2} + \frac{{1 - \sqrt {1 + (1 - 2{p_k}){b_0}{J_m} + \displaystyle\frac{1}{4}b_0^2J_m^2} }}{{{b_0}}}$ |
当
| ${J_k} = \frac{{{J_m}}}{2} + \frac{{1 - \sqrt {1 + (1 - 2{p_k}){b_0}{J_m} + \displaystyle\frac{1}{4}b_0^2J_m^2} }}{{{b_0}}}$ |
| ${J_m} = \frac{{J_m{{^*}} \cdot {L{{^*}}}}}{{{L_s}}}\;{J_k} = \frac{{J_k{{^*}} \cdot {L{{^*}}}}}{{{L_s}}}$ |
| ${b_{11}} = 4\frac{{1 - {p_k}}}{{\left( {{J_m} - {J_k}} \right){J_k}}} - 2\frac{{{p_k}}}{{J_k^2}}$ |
| ${b_{21}} = - 2\frac{{1 - {p_k}}}{{{{\left( {{J_m} - {J_k}} \right)}^2}}}$ |
| ${b_{22}} = - {b_{21}}{J_m}$ |
所计算舱或舱组的前后界限不与前后断点重合:
| $J \leqslant {J_k}:p\left( {{x_1},{x_2}} \right) = {p_1} = \frac{1}{6}{J^2}\left( {{b_{11}}J + 3{b_{12}}} \right)$ |
| $\begin{array}{l}J \! > \! {J_k}:p\left( {{x_1},{x_2}} \right) \! = \! {p_2} \! = \! - \displaystyle\frac{1}{3}{b_{11}}J_k^3 \! +\! \displaystyle\frac{1}{2}\left( {{b_{11}}J - {b_{12}}} \right)J_k^2 + {b_{12}}J{J_k} - \\\qquad \displaystyle\frac{1}{3}{b_{21}}\left( {J_n^3 - J_k^3} \right) + \displaystyle\frac{1}{2}\left( {{b_{21}}J - {b_{22}}} \right)\left( {J_n^2 - J_k^2} \right) + {b_{22}}J\left( {{J_n} - {J_k}} \right)\end{array}$ |
所计算的舱或舱组的后部界限与后端点重合或所计算的舱或舱组的前部界限与前端点重合:
| $\begin{aligned}& J \leqslant {J_k}:p\left( {{x_1},{x_2}} \right) = \displaystyle\frac{1}{2}\left( {{p_1} + J} \right)\\& J > {J_k}:p\left( {{x_1},{x_2}} \right) = \displaystyle\frac{1}{2}\left( {{p_2} + J} \right)\end{aligned}$ |
大部分船舶存在边舱。边舱可以保护内侧舱室不破损,也可装载压载水调整船舶浮态。边舱对破损稳性也有很大影响。在处理边舱时采用因子
| $r\left( {{x_{1,}}x_2^{},b} \right) = 1 - \left( {1 - C} \right)\left[ {1 - \frac{G}{{p\left( {{x_1},{x_2}} \right)}}} \right]$ |
式中:
如所计算的舱或舱组的界限不与后端点或前端点重合,则
| $G = {G_2} = - \frac{1}{3}{b_{11}}J_0^3 + \frac{1}{2}\left( {{b_{11}}J - {b_{12}}} \right)J_0^2 + {b_{12}}J{J_0}$ |
式中
如所计算的舱或舱组的后部界限与后端点重合或前部界限与前端点重合,则
| $G = \frac{1}{2} \cdot \left( {{G_2} + {G_1} \; J} \right)$ |
若水线以上存在水平分隔,对于水平分隔以下的舱或舱组,其
| $V_m = V(H_{j,n,m,}d) - V(H_{j,n,m} {_{- 1,}}d)$ |
当
| $V_{(H,d)} = \frac{{0.8(H - d)}}{{7.8}}$ |
其他情况:
| $V_{(H,d)} = 0.8 + \frac{{0.2((H - d) - 7.8)}}{{4.7}}$ |
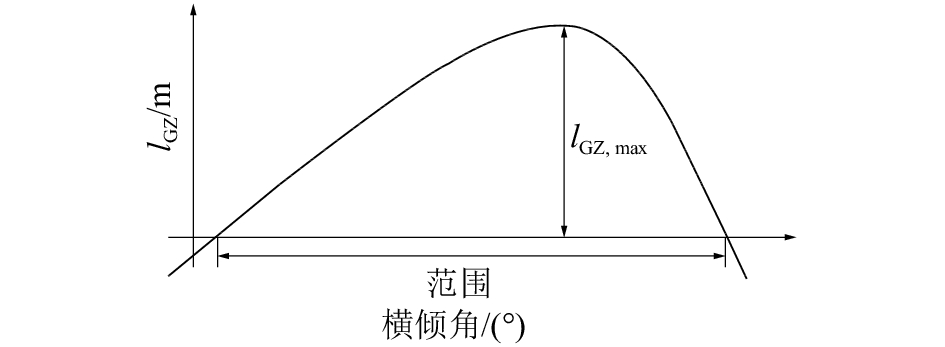
初始装载工况下破损情况的因数S为
| ${s_i} = \min \{ {s_{{\rm{intermediate}},i}},{s_{{\rm{final}},i}},{s_{{\rm{mom}},i}}\} $ |
式中:
|
Download:
|
| 图 2 扶摇礼毕-横倾角曲线 | |
在maxsurf中可构建破舱稳性数值计算模型,船体外板由船艏、船艉和中部的平行中体3部分构成,通过设定控制点设定船舶主尺度为长200 m、宽30 m、型深17.85 m,控制点如图 3所示,其他尺度如表1所示。对建立好的模型进行渲染,可得到货船的3D模型图如图 4。

|
Download:
|
| 图 3 船模控制点 | |

|
Download:
|
| 图 4 船模3D渲染图 | |
|
|
表 1 某货船主尺度 |
将此船3D模型进行舱室划分,对建好的模型进行辅助板的添加,添加辅助板后的船体渲染图如图 5所示。

|
Download:
|
| 图 5 添加辅助板后的模型 | |
输入舱室名称、舱室类型(液舱输入液体密度)、舱室坐标系等要素。初步将船舶划分为货舱(5个)、机舱、艏尖舱、燃料舱、压载水、淡水舱等47个舱室。部分参数见表 2,舱室效果图如图 6所示。
|
|
表 2 舱室划分数据 |

|
Download:
|
| 图 6 舱室划分3D效果 | |
计算A需要3种工况的支撑,分别为最深分舱吃水、部分分舱吃水、轻盈分舱吃水。其中最深分舱吃水为夏季吃水,也就是货船满载的工况,设置为工况1。输入空船重量、重心位置如表 3所示。
|
|
表 3 工况1输入数据 |
定义工况2为船舶带10%的消耗品和必要压载水调整浮态的一种装载情况。定义工况3为部分吃水工况。根据公约
|
|
表 4 输入装载数据 |
3种工况的初始数据如表 5所示。
|
|
表 5 3种工况吃水 |
完成工况输入后,进行纵向、横向、垂向的区域划分,参数设置如表 6~8所示。
|
|
表 6 纵向区域数据 |
|
|
表 7 横向区域数据 |
|
|
表 8 垂向区域数据 |
|
Download:
|
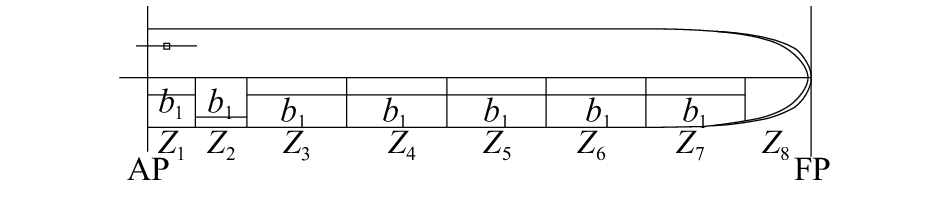
| 图 7 船舶区域划分俯视图 | |

|
Download:
|
| 图 8 船舶垂向区域划分 | |
此货船的多个横向、纵向、垂向界限及位置已确定。这3个方向的多个界限会将整个船舶分为多个小的区域,不同位置的相邻区域还存在组合现象。不同区域内将包含不同数量的舱室,软件将依据设定的区域位置数据,利用第2节介绍的公式进行逐一计算,得到各个中间值,最终将得到各单区域、相邻组合区域的P、r、V值。
根据此货船的概念框架图确定最大相邻破损区域为3个。部分破损的舱室组合如表 9所示,将得到的大量结果进行整理得到结果如表 10所示。
|
|
表 9 工况1下破损舱室组合 |
|
|
表 10 概率破舱稳性计算结果 |
计算结果如表 11所示。计算流程为首先计算单区域破损,整体上从
|
|
表 11 计算过程简表 |
2)在最深分舱吃水下,计算获得的A值为0.583 1,满足规范要求。对具体区域结果进行分析可以看出,在工况1中,区域7破损时的全部舱室组合残存概率S全为0,对最终结果A无贡献,因此Z7的舱室划分不合理(1货舱较大,破损后残存概率低)。此时可根据SOLAS 09的要求进行处理。
将Z7内的全部舱室沿纵向等分为2个货舱,同时划分为Z7和Z8,重新进行计算得到分舱后的计算结果如表 12。
|
|
表 12 分舱后的计算结果 |
将舱室重新划分后,新划分的
1) 每个破损组合有至少1个中间过程。二者的
2) 最深分舱吃水下的
3)利用SOLAS 2009计算时,要求计算区域内全部的舱室破损。
本文采用maxsurf软件为依托,研究了基于概率性破舱稳性的公约SOLAS 2009,并获得预期结果,对市场上需要重新依据新公约衡量破舱稳性的船舶具有重大意义。对新型船舶,也可在设计阶段进行概率破舱稳性的计算和舱室的优化。
| [1] |
张文广. " 加百利”轮海难救助合同纠纷再审案评析[J]. 法律适用, 2016(8): 42-45. ( 0) 0)
|
| [2] |
李世锋. 从客船视角谈大规模海难救助的几点思考[J]. 航海, 2016(6): 53-56. ( 0) 0)
|
| [3] |
盛振邦, 杨尚荣, 陈雪深. 船舶静力学[M]. 上海:上海交通大学出版社, 1988.
( 0) 0)
|
| [4] |
PAPANIKOLAOU A, ELIOPOULOU E. On the development of the new harmonised damage stability regulations for dry cargo and passenger ships[J]. Reliability engineering & system safety, 2008, 93(9): 1305-1316. ( 0) 0)
|
| [5] |
马涅采夫H Я. 船舶不沉性理论[M]. 键链, 译. 北京: 国防工业出版社, 1977.
( 0) 0)
|
| [6] |
邹梦瑶. 水面舰船破损稳性的概率评估方法研究[D]. 大连: 大连理工大学, 2016.
( 0) 0)
|
| [7] |
中国船舶工业集团公司, 中国船舶重工集团公司, 中国造船工程学会. 船舶设计实用手册: 总体分册[S]. 3版. 北京: 国防工业出版社, 2013.
( 0) 0)
|
| [8] |
中国船级社, 国际海上人命与安全中国船级社. SOLAS 2009分舱与破损稳性要求实施指南[M]. 北京:人民交通出版社, 2009.
( 0) 0)
|
| [9] |
王侨. SOLAS 2009概率破损稳性方法应用研究[D]. 大连: 大连理工大学, 2011.
( 0) 0)
|
| [10] |
黄武刚. 基于FORAN的船舶概率破舱稳性计算分析[J]. 中国造船, 2015, 56(S1): 177-184. ( 0) 0)
|
| [11] |
周晓明. 基于概率破舱稳性的驳船优化分舱研究[D]. 大连: 大连理工大学, 2006.
( 0) 0)
|
| [12] |
陈晓娜. 客滚船概率破舱稳性计算分析[J]. 船舶设计通讯, 2017(2): 24-29. DOI:10.3969/j.issn.1001-4624.2017.02.006 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


