拖缆机机架作为拖缆机上支撑类的重要零件，在拖缆机工作过程中起着支撑拖缆机各部件重力和固定相对位置的作用，同时，机架质量通常占整机质量的10%~15%。针对现有船用大型拖缆机结构优化问题,采用多目标拓扑优化方法对大型拖缆机机架进行概念设计。拖缆机机架的优化目标主要有刚度、固有频率、重量三个方面。为了解决拖缆机机架的结构多刚度和固有频率之间的不一致性和不可协调性，本文采用折衷规划法对其进行多目标优化设计。折衷规划法是一种解决多目标规划问题的数学规划方法。由于结构优化的各目标函数之间的冲突，不能保证所有目标函数都为最优解，折衷规划法的基本思想是获得实际目标点到理想点的最短距离。

利用折衷规划法或其他数学规划法的多目标优化法在结构优化实际工程中也得到了广泛的应用，如：武汉理工大学的赵新浩等^[1]对机床机架进行多目标优化设计。南昌大学的辛勇^[2]对汽车的车架利用多目标优化方法进行了优化设计，在刚度和模态方面都得到了改善。向湘林等^[3]利用SIMP材料插值方法，分别以刚度最大和低阶模态固有频率最大作为优化目标建立拓扑优化模型对车架进行了优化设计。大连理工大学的王成林^[4]在其硕士论文中对起重机桁架臂进行多目标拓扑优化。方子帆等^[5]以支撑结构为对象，研究了多工况下结构材料的最优布局和结构固有频率最大化的多目标优化问题。对于连续体的动态拓扑优化优化问题在结构优化领域一直备受关注。胡世军等^[6]利用ANSYS对主轴箱体进行了模态分析和拓扑优化；清华大学的范文杰等^[7]利用了基于折衷规划法的多目标优化方法对汽车车架进行了相关理论的研究；华南理工大学亚热带建筑科学国家重点实验室的高兴军等^[8]为消除这种虚假模态产生的不利影响，提出了移频与虚假模态识别相结合的通用方法；悉尼科技大学的罗震教授等^[9]对飞行导弹的整体结构进行了多目标拓扑优化，并且以其前几阶固有频率作为其中的一个优化目标。

1 静载荷多工况拓扑优化

最大刚度的拓扑优化问题是一个在设计空间内追求材料最佳分布的过程。有多个工况作用于一个零件的拓扑优化问题称为多刚度问题。每一种工况对应于一种材料的分布形式，不同的工况载荷得到不同的结构形式^[7]。因此，多刚度问题是一个多目标优化问题。通常的做法是将多个目标函数通过加权法变为一个目标函数，各目标函数通过改变权重可以获得一个帕累托解集，在优化软件OptiStruct中是采用的这种算法实现多个目标优化。但是对于非凸问题，这种方法不能保证获得每一个目标函数都获得最优解。当受到的载荷数量级差别很大时，只通过改变权重的方法不能够很好地平衡各个目标函数。随着迭代次数的增加，受到小载荷的材料分布路径有可能被逐渐忽略掉，可能会得到一个不准确的拓扑结构和一个错误的刚度矩阵。为了克服这种算法的缺陷，本文使用折衷规划法来解决非凸问题和载荷数量级差别大所带来的求解不合理的问题。折衷规划法的核心是各个目标函数逐渐逼近到各自的最佳理想点，各个目标函数通过实际值到理想点的最短距离获得最优解。

基于折衷规划法的目标函数可以表示成^[9]：

$\begin{aligned}C\left( X \right) = & {\left( {\sum\limits_{K = 1}^m {\omega _k^q{{\left( {\frac{{{C_x}\left( X \right) - C_k^{\min }}}{{C_k^{\max } - C_k^{\min }}}} \right)}^q}} } \right)^{\frac{1}{q}}} = \\& \left( {\omega _1^q} \right.{\left( {\frac{{{C_1}\left( X \right) - C_1^{\min }}}{{C_1^{\max } - C_1^{\min }}}} \right)^q} + \cdots + \\& {\left. {\omega _m^q{{\left( {\frac{{{C_m}\left( X \right) - C_m^{\min }}}{{C_m^{\max } - C_m^{\min }}}} \right)}^q}} \right)^{\frac{1}{q}}}\end{aligned}$

式中： ${C_k}\left( X \right)$ 表示第k个工况的目标函数， $C_k^{\min }$ 和 $C_k^{\max }$ 分别表示 ${C_K}\left( X \right)$ 在可行域内的最小值和最大值， ${\omega _k}$ 表示权值并且非负，q为惩罚指数并且大于等于2。

本文中对于作用于拖缆机机架上的静态多刚度载荷可以表示为

$\begin{gathered} {\rm{Min}}:C\left( X \right) = {\left( {\sum\limits_{k = 1}^m {\omega _k^q{{\left( {\frac{{{C_k}\left( X \right) - C_k^{\min }}}{{C_k^{\max } - C_k^{\min }}}} \right)}^q}} } \right)^{\frac{1}{q}}} \\ \operatorname{s} .{\rm t}.\left\{ \begin{gathered} \sum\nolimits_{k = 1}^m {\left( {\sum\nolimits_{j = 1}^n {{V_j}x_j^k} } \right) - \overline V \leqslant 0} \\ 0 < {x_{\min }} \leqslant {x_j} < 1 \\ j = 1,2, \cdots ,n;k = 1,2, \cdots ,m \\ \end{gathered} \right. \\ \end{gathered} $

(1)

式中：x代表设计变量，m为载荷的个数，n为单元个数， $\omega $ 代表权值， $\overline V $ 代表可设计区域的体积。

2 动态载荷拓扑优化

在拖缆机工作过程中，由于振动给机架带来的疲劳是拖缆机在使用过程中一个需要考虑的重要问题。拖缆机所受到的外界激励频率在110 Hz左右，与拖缆机机架的固有频率大致相等。本文通过拓扑优化的方法提高拖缆机支架的前4阶平均固有频率，使零件的固有频率远离外界的激励频率，从而减少设备工作过程中共振现象。

本文中对于零件的模态优化分析可以表述为

$\left\{ \begin{gathered} \max :{\lambda _n} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{gathered} \sum\nolimits_{j = 1}^n {{V_j}{x_j} - \overline V \leqslant 0,j = 1,2, \cdots ,n} \\ 0 < {x_{\min }} \leqslant {x_j} < 1,j = 1,2, \cdots ,n \\ \left( {{K} - {\lambda _n}{M}} \right){{\phi }_n} = \left\{ 0 \right\} \\ \end{gathered} \right. \\ \end{gathered} \right.$

式中： ${\lambda _n}$ 代表零件的平均固有频率，x代表设计变量，n为单元个数， ${K}$ 代表系统的刚度矩阵， ${M}$ 代表系统的质量矩阵， ${{\phi }_n}$ 代表第n阶的正交特征向量， $\overline V $ 代表可设计区域的体积。

3 静态与动态载荷联合多目标优化

结构多目标拓扑优化技术是将多目标优化技术应用于结构优化领域。产品初级设计阶段就应考虑多目标优化问题，使设计更具有针对性，从而获得更好的性能，因此结构多目标拓扑优化技术是近年来各领域都在争先研究的领域^[10-12]。本问题中要求静态多刚度拓扑优化中的柔度目标最小，同时模态拓扑优化中的平均固有频率最大，所以必须对多个目标函数进行处理才能实现对拖缆机机架的多目标拓扑优化。本文使用折衷规划法将多个目标函数整合为一个目标函数，并根据经验对各个目标函数添加权值，使用的等式如下：

$\begin{array}{l}\min F\left( X \right) = \left( {\sum\limits_{k = 1}^m {{\omega _k}{{\left( {\displaystyle \frac{{{C_K}\left( X \right) - C_K^{\min }}}{{C_K^{\max } - C_K^{\min }}}} \right)}^2}} } \right. + \\{\kern 1pt}\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\;\left( {1 - \sum\limits_{k = 1}^m {{\omega _k}} } \right){{\left( {\displaystyle \frac{{{\varLambda _{\max }} - {\varLambda _\lambda }}}{{{\varLambda _{\max }} - {\varLambda _{\min }}}}} \right)}^2}} \right)^{\frac{1}{2}}}\end{array}$

(2)

式中： ${C_k}\left( X \right)$ 为静态刚度工况下的目标函数值， $C_k^{\min }$ 为第k个工况下的最小柔度， $C_k^{\max }$ 为第k个工况下的最大柔度值， ${\varLambda _{\max }}$ 为拖缆机卷筒支撑侧板的最大平均固有频率， ${\varLambda _{\min }}$ 为改进前的最大平均固有频率， ${\varLambda _{\left( \lambda \right)}}$ 为模态拓扑优化中的目标函数。

4 拖缆机机架多目标优化设计 4.1 边界条件及载荷工况

静态多工况与模态分析结合的多目标拓扑优化方法应用于拖缆机机架的结构优化中。拖缆机机架作为拖缆机中的重要零件有必要对其进行改善和优化。我们将考虑机架上的一些重要载荷工况，包括卷筒部件重力、电机重力、减速器重力和钢丝绳通过卷筒传递到机架的倾覆力矩等重要载荷工况，并将力矩转化垂直方向的作用力。将式（1）和（2）利用hypermath导入到OptiStruct中进行多目标拓扑优化设计。OptiStruct是目前世界上广泛应用的关于优化设计的商用软件之一，它为工程优化设计提供了一种简单易学的方法。图1中底部为拖缆机机架。

采用折衷规划法取代加权法对拖缆机机架进行结构拓扑优化设计。图2为经过简化后的拖缆机机架的有限元模型，模型采用六面体网格对支撑侧板进行网格划分，这样的优点是网格数量较少、网格质量好并且求解速度快，可以有效地提高计算效率。图中R区域为非设计区域，B区域为设计区域。材料的弹性模量为206 MPa，材料的密度为7.9×10³ kg/m³，泊松比为0.3。

4.2 优化结果

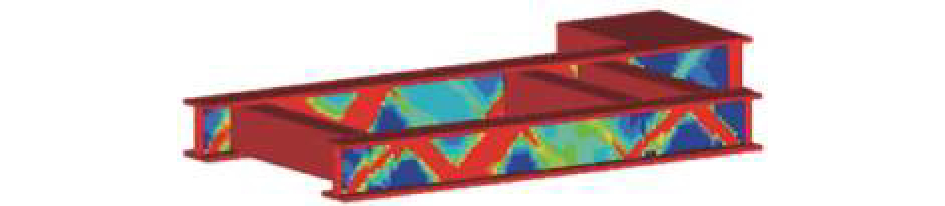
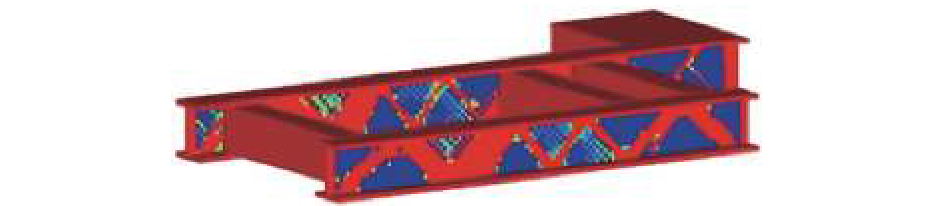
在OptiStruct软件进行求解。得到优化迭代单元密度变化过程如图3、4所示，通过密度图可以看出承受多个载荷的拖缆机机架的具体传力路径。在密度图3、4中直线所围区域为密度接近于0，可以相应地去除材料，其他区域为密度接近或等于1，应为保留部分。通过密度图对拖缆机支架进行再设计，实现减重、提高刚度和提高固有频率的优化目标。

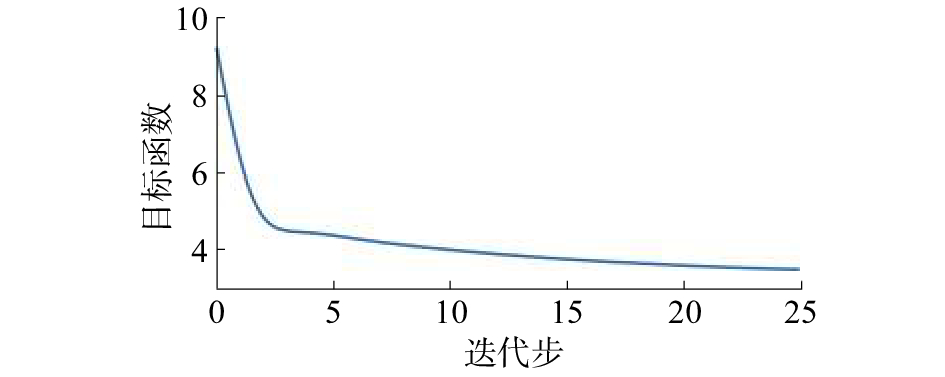
图5表示目标函数的变化曲线，从图中可以看出在前5次迭代中，目标函数有明显的降低；在迭代15次以后目标函数区域收敛；迭代到第25次，计算结束得到收敛结果。

表1为优化前后拖缆机的体积、重量、柔顺度（结构刚度）、平均固有频率的变化，通过优化拖缆机机架的各项性能都得到了一定程度的改善。

图6是参照拖缆机机架的单元密度图重新设计的CAD三维模型。对优化后的模型再次进行仿真分析，经过优化模型的各项性能相对于初始的零件结构都得到改善。

5 结论

1）应用折衷规划法将多目标拓扑优化用于大型拖缆机机架的结构设计中，完成了拖缆机机架的概念设计。

2）经过优化后的拖缆机机架在性能上都得到了改善，其质量减少了10.7%，柔顺度降低了2.92，前4阶的平均固有频率提高了22 Hz。

3）证明了基于动态和静态的多工况多目标拓扑优化方法在海工装备设计过程中的实用性。

4）通过对拖缆机机架的优化设计为其他海工装备的结构优化设计提供理论参考。