收稿日期:2018-03-29;网络出版日期:2018-05-03
基金项目:国家自然科学基金项目(61271074)
作者简介:赵应盛(1992−),男,硕士研究生;
刘长军(1973−),男,教授.
School of Electronics and Information Engineering, Sichuan University, Chengdu 610064, China
目前,能源问题正在受到人们越来越多的重视,微波无线能量传输(MPT)是实现能量无线传输的一项关键技术,引起了国内外广泛研究[1-2]。微波无线能量传输系统将电能转化为微波,经过空间传输,由接收端将微波接收并转化为直流电能。根据天线阵理论,微波发射端天线阵列单元辐射的相位差异决定了波束合成和波束指向,会影响系统的传输效率。因此,需要调整微波发射端天线阵元的相位,提升接收功率,从而提高无线能量传输的效率。在常规调相过程中,对于一个有N×N个阵元的天线阵,需要配备N×N个6位移相器,假设完成一次移相并获得总接收功率的时间为T,通过枚举法对各阵元进行波束寻优调整,需要的时间为64N×NT
才能最大化接收功率。该方法可以寻找到最优相位分布,但对于大型天线阵的调整耗时非常长。基于智能算法(遗传算法、粒子群算法等)的天线阵列波束优化法已经广泛应用于实践中[3]。但在实际工程中,若优化模型设置不合理,优化效果便无法满足工程需求。同时,若算法的收敛速度不稳定,优化时间便不稳定。通常情况下,这类智能方法需要的测试时间较长[4]。为了进一步减少测试时间,文献[5]采用了阵元相位“迭代”的方法提升接收功率,耗时降低至64N2T。
REV法作为一种基于功率分析的天线阵列校准方法,非常适用于MPT领域的发射天线阵相位优化。本文研究了一种基于REV的相位优化方法,在保证传输效率有效提高的条件下,将优化时间降低至(2×N2+1)T。与传统方法相比,大幅度地缩短了发射天线阵元相位优化时间,且优化时间稳定。
1 旋转矢量法原理
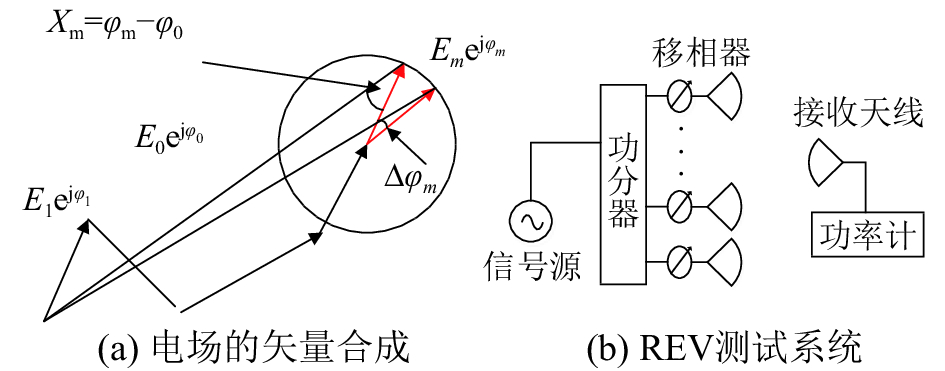
旋转矢量法是一种基于功率分析的天线阵元相位校准方法[6]。该校准方法硬件要求低,且无需考虑天线阵元之间的互耦情况,目前已被应用于工程实践中,是一种有效的相位优化方法。从理论上讲,该方法可以使接收天线处的接收功率最大化,具体原理如图1所示。其中,E0和
${\varphi _0}$
为合成场矢量的幅度值和相位,Em和
${\varphi _m}$
为第m个阵元的电场幅度和相位,
${E_{\overline m }}$
和
${\varphi _{\overline m }}$
为其他阵元(除去第m个阵元)的合成电场的幅度和相位,
$\Delta {\varphi _m}$
为第m个阵元的相移量。利用矢量合成关系,得到:
|
$ \begin{array}{c}P = {E_0}^{\rm{2}} = {E_{\overline m }}^2 + {E_m}^{\rm{2}} + \\ 2{E_{\overline m }}{E_m}{\rm{cos}}\left( {{\varphi _{\overline m }} - {\varphi _m}{\rm{ + }}\Delta {\varphi _m}} \right)\end{array} $
|
(1) |
式中P为合成场的功率值。
归一化的阵元电场由式(2)给出。
|
$ \frac{{{E_m}}}{{{E_0}}}{{\rm{e}}^{{\rm{j}}({\varphi _m} - {\varphi _0})}} = \frac{{{E_m}{{\rm{e}}^{j{\varphi _m}}}}}{{{E_m}{{\rm{e}}^{j{\varphi _m}}} + {E_{\overline m }}{{\rm{e}}^{j{\varphi _{\overline m }}}}}} = \frac{{{E_m}}}{{{E_m} + {E_{\overline m }}{{\rm{e}}^{j\left( {{\varphi _{\overline m }} - {\varphi _m}} \right)}}}}\;\;\;\;\; $
|
(2) |
根据实际情况,采用不同位数的移相器,通过线性拟合或离散傅里叶变换,得到各阵元的相位调控值
${\varphi _m} - {\varphi _0}$
,具体可参考文献[7-8]。
从式(1)可知,当改变
$\Delta {\varphi _m}$
,P随之改变,利用3组不同的(
$\Delta {\varphi _m}$
,P),联立式(1)、(2)便可得到第m个阵元需要调整的相移量
${\varphi _m} - {\varphi _0}$
。为了简化计算,文献[9]将每个阵元移相值取为0°、90°、180°,对应的功率分别表示为P0、Pπ/2、Pπ,由式(3)~(6)给出。简化后得到式(7)~(9),利用矩阵计算便可得到相移量
${\varphi _m} - {\varphi _0}$
。此方法仅需采用2位的移相器,进一步降低了测试成本。
|
$\begin{split} {P_0} = & ({E_{\overline m }}{{\rm{e}}^{{\rm{j}}{\varphi _{\overline m }}}} + {E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} + 0)}}){({E_{\overline m }}{{\rm{e}}^{{\rm{j}}{\varphi _{\overline m }}}} + {E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} + 0)}})^*} = \\ & ({E_{\overline m }}^2 + {E_m}^2) + {E_{\overline m }}{E_m}{{\rm{e}}^{{\rm{j}}({\varphi _{\overline m }} - {\varphi _m})}} + {E_{\overline m }}{E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} - {\varphi _{\overline m }})}}\;\;\;\;\;\;\; \\ \end{split}$
|
(3) |
|
$\begin{split} {P_{{\rm{\pi }}/2}} = & ({E_{\overline {\rm{m}} }}{{\rm{e}}^{{\rm{j}}{\varphi _{\overline m }}}} + {E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} + {\rm{\pi }}/2)}}){({E_{\overline m }}{{\rm{e}}^{{\rm{j}}{\varphi _{\overline m }}}} + {E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} + {\rm{\pi }}/2)}})^*} = \\ & ({E_{\overline m }}^2 + E_m^2) + {E_{\overline m }}{E_m}{{\rm{e}}^{{\rm{j}}({\varphi _{\overline m }} - {\varphi _m})}}{{\rm{e}}^{ - {\rm{j\pi }}/2}} + {E_{\overline m }}{E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} - {\varphi _{\overline m }})}}{{\rm{e}}^{{\rm{j\pi }}/2}} \end{split} $
|
(4) |
|
$\begin{split} {P_{\rm{\pi }}} = & ({E_{\overline m }}{{\rm{e}}^{{\rm{j}}{\varphi _{\overline m }}}} + {E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} + {\rm{\pi }})}}){({E_{\overline m }}{{\rm{e}}^{{\rm{j}}{\varphi _{\overline m }}}} + {E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} + {\rm{\pi }})}})^*} = \\ & ({E_{\overline m }}^2 + {E_m}^2) + {E_{\overline m }}{E_m}{{\rm{e}}^{{\rm{j}}({\varphi _{\overline m }} - {\varphi _m})}}{{\rm{e}}^{ - {\rm{j\pi }}}} + {E_{\overline m }}{E_m}{{\rm{e}}^{{\rm{j}}({\varphi _m} - {\varphi _{\overline m }})}}{{\rm{e}}^{j{\rm{\pi }}}} \end{split} $
|
(5) |
|
${{P}} = {\left( {\begin{array}{*{20}{c}} {{P_0}}&{{P_{{\rm{\pi }}/2}}}&{{P_{\rm{\pi }}}} \end{array}} \right)^{\rm{T}}}$
|
(6) |
|
${{A}} = \left( {\begin{array}{*{20}{l}} 1& \;\;\; 1& \;\,\,\, 1 \\ 1& \;\! { - {\rm{j}}}& \;\;\; {\rm{j}} \\ 1&{ - 1}&{ - 1} \end{array}} \right)$
|
(7) |
|
$\begin{split} {{Z}} = & {\left[ {{z_1}\;{z_2}\;{z_3}} \right]^{\rm{T}}} = \\ & [\left( {{E_{\overline m }}^2 + {E_m}^2} \right)\;{E_{\overline m }}{E_m}{{\rm{e}}^{{\rm j}({\varphi _{\overline m }} - {\varphi _m})}}\;{E_{\overline m }}{E_m}{{\rm{e}}^{{\rm j}({\varphi _m} - {\varphi _{\overline m }})}}]\end{split} $
|
(8) |
|
${{Z}} = {{{A}}^{{\rm{ - }}1}}{{P}}$
|
(9) |
REV方法简便,但会引入求解的二义性,即存在2个解。文献[10]对目前国内外已提出的消除旋转矢量法解的二义性的方法进行了总结,并提出了一种新的解决方法。该消除方法在无线能量传输系统中并不适用。在实际的无线传输系统应用中,优化阵元相位时,可以实时测试得到接收端输出的功率值。本文提出消除二义性的方法为:将2个不同的解引入测试系统,通过测试实际的输出功率,优选输出功率高的解为正解。该方法结合了实验测量,在无线能量传输领域中,比常规的方法更快捷。
2 微波无线能量传输系统中的REV
参考图1,若把接收天线的位置定义为校准位置,通过REV法进行优化后,可以使接收天线处的接收功率值最大化,即校准位置的功率最大。然而在实际的微波无线能量传输系统中,接收天线往往尺寸较大,传输距离也不一定满足发射阵列的远场条件,故难以把整个接收天线阵视为一个接收点使其接收功率最大化。若把接收天线设置在接收面上不同的位置,通过REV法进行优化后,整个接收面上优化后的总接收功率会不同,输能系统的传输效率便不同。
为了方便讨论,假设微波无线能量传输系统为:发射天线阵与接收天线阵均为(2N+1)×(2N+1)方型天线阵列(为方便表示,行、列均采为奇数个阵元、偶数个阵元有相同结论);发射和接收天线阵列距离为R;天线阵列的尺寸为L×L;对角线长度(物理最长尺寸)为D,收发天线阵列的阵元均为相同天线;天线工作频率为2.45 GHz,由于不同的传输系统中发射天线阵元各不相同,所以,此处将阵元天线等效为在阵元天线中心点处的点源,阵元天线的相位中心也在点源上,点源之间的间隔为d。MPT输能系统如图2所示,其中黑点代表阵列阵元。
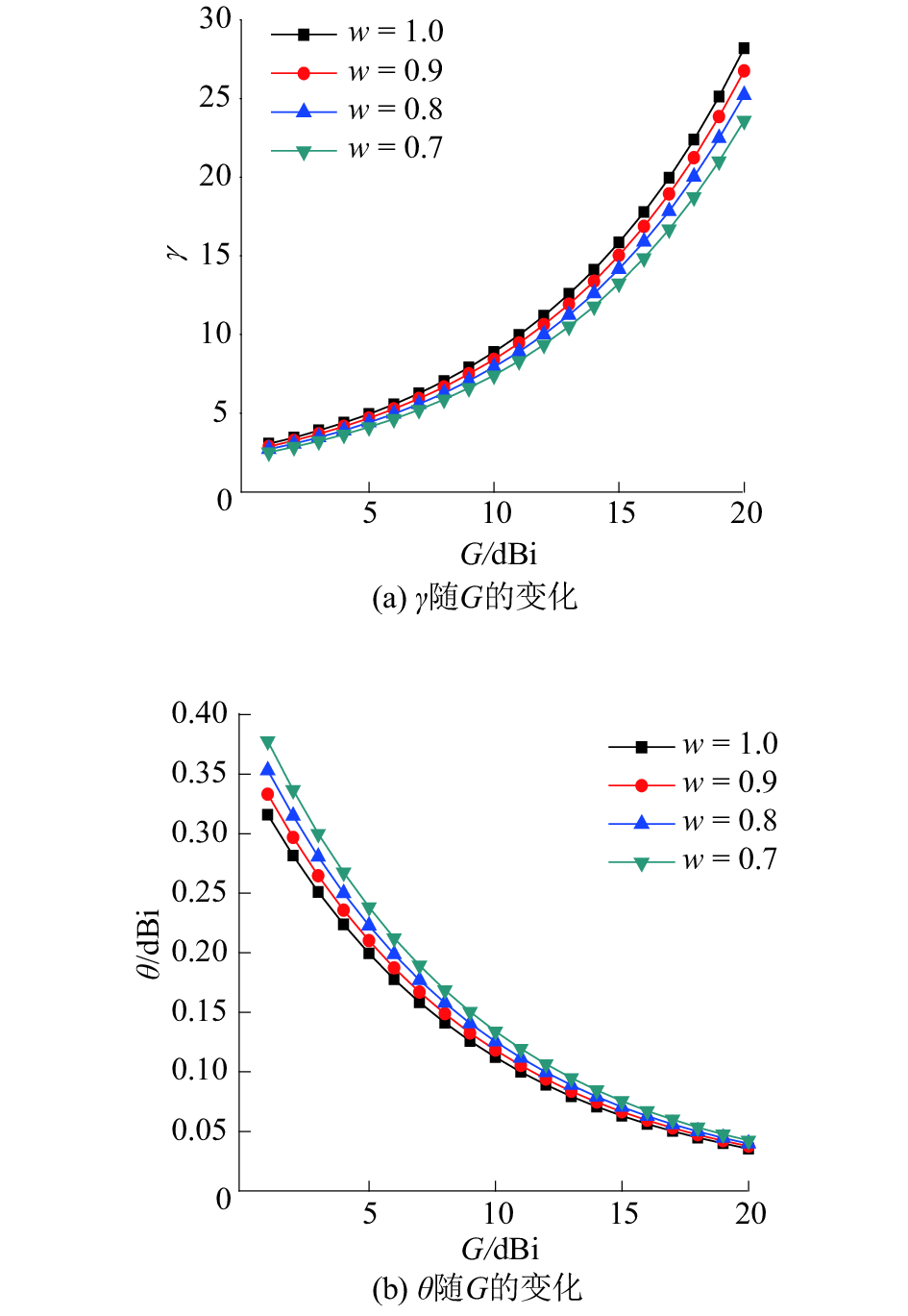
假设单个阵元天线的水平面和垂直面的半功率波瓣角分别为θEP、θHP,且大小一致,天线的效率因子表示为w,阵元天线的增益表示为G。参考图2(c),定义θ为红点阵元到接收面边缘两端的水平夹角,且θ满足式(10)。若令θ为θEP的1/10,即为θEP/10。假设传输距离满足单个阵元的远场条件,根据天线基本理论,得到式(11)。联立式(10)、(11),定义γ,由式(12)给出。计算得到γ和θ随着单个阵元的增益G的变化,如图3所示。
若阵元天线增益G为15 dBi,天线的效率因子w为0.8。根据图3,输能系统的γ仅需大于14.1,波束角θ便可小于0.1°,此时该阵元天线在接收面上的电场幅值可看作一致大小。若γ足够大,其他位置阵元也有同样结论。
|
$\cot \theta = \frac{R}{L}$
|
(10) |
|
$G = \frac{{41 \; 253}}{{{\theta _{EP}}{\theta _{HP}}w}}$
|
(11) |
|
$\gamma = \frac{R}{L}{\rm{ = }} = \cot \left( {\sqrt {\frac{{41 \; 253}}{{Gw}}} /10} \right)$
|
(12) |
在实际的MPT工程中,接收阵列的面积受限,传输距离也满足单个发射阵元的远场条件,输能系统中的γ较大[11]。所以,假设图2系统满足下列条件:1)传输距离R满足单个发射阵元的远场条件;2)系统的γ足够大,阵元在接收面上的电场幅值近乎一致。由此,给出下列参数定义:
天线阵元(x,y)为在第x行第y列的天线阵元,其中
$x{\rm{,}}y \in [ - N,N]$
;Ekg_ij为发射天线阵元(k,g)在接收天线阵元(i,j)处产生的电场幅值,Ekg_ij在接收面均匀分布且与传输距离R成反比,故可令Ekg_ij为1/R;Eij_total和θij_total为接收天线阵元(i,j)处的电场幅值和相位;Ptotal和Ptotal_REV分别表示利用REV优化前和优化后的总接收功率,此处的总接收功率是指接收阵元的接收功率的总和;θkg_ij为发射阵元(k,g)在接收阵元(i,j)处产生的电场相位,类似表示可同理类推;θab为以(a,b)为校准位置,各阵元合成电场的相位,a、b连续可变,有
$a,b \in [ - N,N]$
,其中以(a,b)为校准位置可以理解为把图2(c)中接收端(a,b)处阵元作为接收天线,进行波束调整;
$\Delta {\phi _{kg\_ij\_ab}}$
为发射阵元(k,g)分别到接收阵元(i,j)和到接收天线(a,b)的相位差,如式(13)表示,
$\Delta {\phi _{kg\_ij\_ab}}$
对a求偏导,得到式(14)。利用REV法前后的接收端总功率分别表示为式(15)、(16)。G(a)对a求偏导,得到F(a),由式(17)、(18)联立可得。
|
$\begin{split} \Delta {\phi _{kg\_ij\_ab}} = & \frac{{2{\rm{\pi }}}}{\lambda }\sqrt {{{\left[ {(k - i)d} \right]}^2} + {{\left[ {(g - j)d} \right]}^2} + {R^2}} - \\ & \frac{{2{\rm{\pi }}}}{\lambda }\sqrt {{{\left[ {(k - a)d} \right]}^2} + {{\left[ {(g - b)d} \right]}^2} + {R^2}}\end{split} $
|
(13) |
|
$\Delta {\phi _{kg\_ij\_ab}}{^\prime _a} = \frac{{2{\rm{\pi }}d(k - a)}}{{\lambda \sqrt {{{[(k - a)d]}^2} + {{[(g - b)d]}^2} + {R^2}} )}}\;\;\;\;\;$
|
(14) |
|
$\begin{split} {P_{{\rm{total}}}} = & \sum\limits_{i = - N}^N {\sum\limits_{j = - N}^N {{{\left| {{E_{ij\_{\rm{total}}}}{{\rm{e}}^{{\rm{j}}{\theta _{ij\_t{\rm{total}}}}}}} \right|}^2}} } = \\ & {\sum\limits_{i = - N}^N {\sum\limits_{j = - N}^N {\left| {\sum\limits_{k = - N}^N {\sum\limits_{g = - N}^N {{E_{kg\_ij}}} {{\rm{e}}^{{\rm{j}}{\theta _{kg\_ij}}}}} } \right|} } ^{\rm{2}}}\end{split} $
|
(15) |
|
$\begin{split}G(a) = & {P_{{\rm{total}}}}{\__{{\rm{REV}}}} = \\& \sum\limits_{i = - N}^N {\sum\limits_{j = - N}^N {\left\{ {{{\left| {\sum\limits_{k = - N}^N {\sum\limits_{g = - N}^N {{E_{kg\_ij}}} } {{\rm{e}}^{{\rm{j}}({\theta _{kg\_ij}} + ({\theta _{ab}} - {\theta _{kg\_ab}}))}}} \right|}^2}} \right\}} } {\rm{ = }}\\& \sum\limits_{i = - N}^N {\sum\limits_{j = - N}^N {\left\{ {{{\left| {\sum\limits_{k = - N}^N {\sum\limits_{g = - N}^N {{E_{kg\_ij}}} } {{\rm{e}}^{j(\Delta {\varphi _{kg\_ij\_ab}} + {\theta _{ab}})}}} \right|}^2}} \right\}} } {\rm{ = }}\\& \sum\limits_{i = - N}^N {\sum\limits_{j = - N}^N {\left\{ {{{\left| {\sum\limits_{k = - N}^N {\sum\limits_{g = - N}^N {{E_{kg\_ij}}} } {{\rm{e}}^{{\rm{j}}\Delta {\varphi _{kg\_ij\_ab}}}}} \right|}^2}} \right\}} } n\end{split}$
|
(16) |
|
$\begin{split} F(a) = & \frac{{\partial {\kern 1pt} G(a)}}{{\partial a}} = \\ & 2\sum\limits_{i = {\rm{ - }}N}^N {\sum\limits_{j = {\rm{ - }}N}^N {\{ \sum\limits_{k = - N}^N {\sum\limits_{g = - N}^N {[{E_{kg\_ij}}\Delta {\phi _{kg\_ij\_ab}}{{^\prime }_a}H(a)} } )} } ]\} \end{split} $
|
(17) |
|
$H(a) = \sum\limits_{k' = - N}^N {\sum\limits_{g' = - N}^N {{E_{k'g'\_ij}}\sin (\Delta {\phi _{k'g'\_ij\_ab}} - \Delta {\phi _{kg\_ij\_ab}})} } \;\;\;\;$
|
(18) |
|
$\eta = \frac{{{P_{{\rm{max}}}} - {P_{{\rm{min}}}}}}{{{P_{{\rm{min}}}}}} \times 100{\rm{\% }}$
|
(19) |
根据文献[12]中的理论,对于一个聚焦口径天线,在辐射近场区便可形成聚焦,且在聚焦面上已满足远场方向图的特性。所以,需要分别研究输能系统中辐射近场区和远场区的输能情况。针对图2提出的MPT系统,在满足前面的假设条件下,令N=3,即7×7的收发天线阵列,令收发天线阵尺寸均为1 m×1 m,则D约为1.4 m。根据基本理论[13],得到此天线阵列辐射近场区需大于2.90 m,远场区需大于31.36 m。
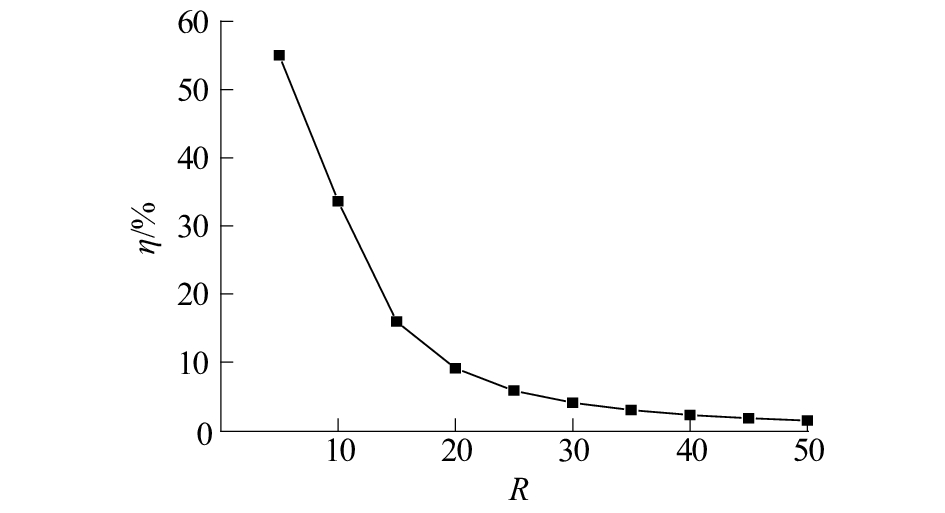
为了满足图2系统的假设条件,取R分别为15、20、25 m(发射阵列的辐射近场区)及35、40、45 m(发射阵列的远场区)。研究归一化的G(a)、F(a)随a的变化趋势,如图4、5所示。令各曲线中的最大值为Pmax,最小值为Pmin,如图4所示。定义变量
$\eta $
,该变量表示在相同传输距离R下,选取接收面上不同的位置进行校准优化,对优化后的总接收功率的影响,具体定义如式(19)。从图4可以看出,在接收平面内,a<0时,F(a)>0,G(a)递增;a≥0时,F(a) ≤0,G(a)递减;所以在a为0时,G(0)为最大值。由于a,b为等效变量,对b进行上述仿真可得到同样的结论。所以,对于图2的系统,当a、b均为0时,即把校准位置设置在接收天线阵列的中心区域,利用REV优化发射天线,可使接收面内的总接收功率更大。由图5可知,在辐射近场区和远场区内,随着传输距离变大,η逐渐变小,说明传输距离越近,校准位置对输能效率影响越大。
3 仿真结果分析
参考上述MPT系统的输能情况分析,下面将从2个方面进行仿真验证:1)不同传输场区下,REV校准法的有效性;2)在相同传输距离下,不同校准位置对微波无线能量传输效率的影响。
若采用不同定向性的阵元,阵列波束的扫描范围和扫描增益等特性会有所不同,考虑到不同MPT系统的工程需求不一样,为了证明方法的有效性,此处采用了2款定向性差异大的天线阵:1)2×2贴片天线阵,单元尺寸为0.06 m×0.06 m,频率2.45 GHz,3 dB波瓣宽度89.9°,天线阵中心坐标为(-0.03,-0.03,0);2)2×2的喇叭天线阵,单元尺寸为0.41 m×0.3 m,频率2.45 GHz,3 dB波瓣宽度8.6°,天线阵中心坐标为(0.23,0.18,0)。利用电磁仿真仿真软件CST,设置各阵元的相位。此处设置为30°、70°、-30°、90°,如图6所示。
3.1 REV在MPT中的有效性
针对图6的模型,根据基本理论,计算得到贴片天线阵的辐射近场区应大于0.12 m,远场区大于0.5 m。喇叭天线阵的辐射近场区应大于1.85 m,远场区大于17.20 m。将校准位置设置为接收面的中心,在感应近场区、辐射近场区、远场区内,通过REV法进行仿真计算,具体数值由表1、2给出(表中的理论最大值为各阵元在校准点的产生电场幅值之和)。结果表明,在感应近场区域(reactive near field,RNF)内,REV效果欠佳。随着距离增大,在辐射近场区和远场区内,校准后的电场幅值十分接近理论最大值,说明在辐射近场区和远场区内,REV法能有效提升MPT传输效率。
表 1(Tab. 1
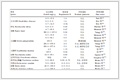
表 1 不同传输距离下REV法的有效性(贴片天线阵)
| 距离X/m
|
优化前E1/(V·m−1)
|
优化后E2/(V·m−1)
|
理论最大值Emax/(V·m−1)
|
$\displaystyle\frac{{{E_2} - {E_1}}}{{{E_1}}}/\% $
|
| 0.05 |
304.53 |
416.68 |
466.37 |
36.83 |
| 0.20 |
127.97 |
179.33 |
181.90 |
40.13 |
| 0.40 |
68.76 |
96.57 |
96.86 |
40.44 |
| 0.60 |
73.22 |
102.82 |
102.96 |
40.44 |
|
表 1 不同传输距离下REV法的有效性(贴片天线阵) |
表 2(Tab. 2

表 2 不同传输距离下REV法的有效性(喇叭天线阵)
| 距离X/m
|
优化前E1/(V·m−1)
|
优化后E2/(V·m−1)
|
理论最大值Emax/(V·m−1)
|
$\displaystyle\frac{{{E_2} - {E_1}}}{{{E_1}}}/\% $
|
| 0.5 |
46.26 |
61.30 |
65.76 |
32.51 |
| 2.50 |
51.53 |
71.61 |
72.53 |
38.97 |
| 5.00 |
22.43 |
32.38 |
32.79 |
44.36 |
| 20.00 |
4.51 |
6.17 |
6.28 |
36.81 |
|
表 2 不同传输距离下REV法的有效性(喇叭天线阵) |
3.2 不同校准位置对无线能量传输效率的影响
从3.1节的结果看,REV法在感应近场区效果不佳,下面的仿真对该场区不予考虑。对于贴片天线阵,将校准位置分别设置左(–0.03, 0,X),中(0, 0, X),右(0.03, 0, X);对于喇叭天线阵,将校准点分别设置左(0, 0.18, X),中(0.23, 0.18, X),右(0.46, 0.18, X),其中X为传输距离,接收面积和发射天线面积等大,具体可参考图7。图中的探针代表接收面上不同位置的接收天线。以不同校准位置的测试数据为参考进行波束优化,优化前后的总接收功率由表3、4给出,其中Poriginal表示为优化前的总接收功率,Pleft、Pmiddle、Pright表示利用左、中、右探针点优化后的接收面的总接收功率。结果表明:以接收面的中心区域充当接收天线,校准发射天线阵波束,接收面的总接收功率最大、传输效率最高。由(Pmiddle–Poriginal)/Poriginal计算得到,贴片天线阵最高提升了96.4%,喇叭天线阵最高提升了47.6%。随着传输距离越近,
$\eta $
越大。故传输距离越近,校准位置的不同对输能效率的影响越大,结论符合MATLAB的仿真结果。
表 3(Tab. 3

表 3 不同校准位置对MPT传输效率的影响(贴片天线阵)
| 距离X/m
|
Pleft/W
|
Pmiddle/W
|
Pright/W
|
Porigina/W
|
$\eta $
/%
|
| 0.20 |
9 438.21 |
11 658.49 |
9 292.26 |
6 043.00 |
25.46 |
| 0.40 |
3 528.16 |
3 955.01 |
3 530.51 |
2 024.15 |
11.96 |
| 0.60 |
1 920.81 |
2 048.79 |
1 920.28 |
1 043.10 |
6.69 |
|
表 3 不同校准位置对MPT传输效率的影响(贴片天线阵) |
表 4(Tab. 4

表 4 不同校准位置对MPT传输效率的影响(喇叭天线阵)
| 距离X/m
|
Pleft/W
|
Pmiddle/W
|
Pright/W
|
Porigina/W
|
$\eta $
/%
|
| 2.50 |
412.81 |
424.54 |
409.87 |
324.06 |
3.58 |
| 5.00 |
338.64 |
343.84 |
337.98 |
257.58 |
1.73 |
| 20.00 |
18.59 |
18.65 |
18.59 |
10.60 |
0.03 |
|
表 4 不同校准位置对MPT传输效率的影响(喇叭天线阵) |
4 实验
利用LabWindows/CVI编写测试程序,搭建微波无线能量传输演示系统。系统中采用相同的2×2收发阵列天线(辐射近场区大于0.75 m,远场区大于8.33 m),该阵列带宽大于1%,半功率波束角小于1°,功率放大器内含6位移相器,系统如图8(a)、(b)所示,测试过程如图8(c)所示。若将文献[5]的方法简称为“迭代法”,本中的方法简称为“三点法”。利用上述2种不同优化法,在不同传输距离下,测试得到优化前后的总接收功率和提升率的数据,如表5所示。测试结果表明:1)在辐射近场区和远场区内,“三点法”可有效提高阵列的总接收功率,且提升效果优于“迭代法”。2)由于测试过程主要时间消耗在移相并获得接收功率的过程中,而完成一次移相并获得接收功率需耗时1 s。若把该过程的耗时设定为测试的总耗时,则“迭代法”所需时间约为256 s,而“三点法”仅需9 s,约为前者优化时间的3%。
表 5(Tab. 5

表 5 不同传输距离下两种优化方法的效果
距离
X/m
|
优化前接收
功率/mW
|
“迭代法”优化后
|
“三点法”优化后
|
接收功率/
mW
|
提升率/% |
|
接收功率/
mW
|
提升率/% |
| 3 |
36.64 |
63.97 |
74.58 |
|
102.57 |
179.90 |
| 5 |
14.83 |
31.91 |
115.28 |
34.51 |
132.81 |
| 7 |
6.75 |
13.30 |
97.24 |
16.41 |
143.22 |
| 9 |
3.74 |
7.98 |
113.30 |
9.91 |
164.85 |
|
表 5 不同传输距离下两种优化方法的效果 |
5 结论
本文研究了一种仅基于功率分析的REV快速相位优化法。对微波无线能量传输系统的仿真和实测结果表明:1)本方法在辐射近场区和远场区内,可有效提高接收功率,实测的功率提升范围为132%~179%;2)本方法优化效果优于文献[5]的“迭代法”,且大幅度地缩短了优化时间,约为后者耗时的3%。





 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2018, Vol. 45
2018, Vol. 45


