2. 试验物理与计算数学国家级重点实验室,北京 100076
2. National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing 100076, China
雷达辐射源信号脉内调制识别是雷达辐射源的重要特征之一,是对敌方雷达辐射源进行截获、分选、识别和定位等非合作通信方式时的重要参数。辐射源信号调制识别存在电磁环境复杂化、调制样式多样化、信噪比低等问题。Zhang Z[1]将高阶累积量和堆叠卷积自动编码器相结合应用于多径衰落信道种的调制分类。王静[2]将压缩感知与高阶循环累积量相结合,在不重构原信号波形的前提下完成调制识别。Fontes[3]提出基于相关熵的决策论算法,在先验知识未知、信噪比高于5 dB条件下有很好的识别效果。Cai T[4]提出一种星座小波变换自动识别器,其依据QAM星座特点以最合适的尺度对接收信号进行Haar小波变换从而进行调制识别。李强[5]通过AP聚类方法对均衡后的信号星座图进行聚类提出一种有限类型调制识别方法。熊坤来[6]将信号时频图像灰度值矩阵拉直作为图像特征实现对多种LPI雷达信号的准确识别,但亦存在数据维数高、计算量大的问题。白航[7]使用时频分析方法得到信号的时频图像,再使用Hu矩、伪Zernike矩从预处理后的二值图像提取图像特征,完成分类算法,该方法依然存在低信噪比识别率低的问题。上述几种调制识别方法都存在着运算复杂度高、低信噪比下识别率低的问题。
本文引入Wigner-Ville分布改进后的Choi-Williams分布(Choi-William distribution, CWD),使用CWD将雷达辐射源信号从一维时域信号转换为二维时频域的时频图像,应用图像处理技术提取时频图像中的辐射源信号的调制特征。针对不同信噪比情况下时频图像中的交叉项和噪声的不同表现方式,提出一种将二阶四阶矩估计法与主成分分析(principal component analysis, PCA)相结合的自适应主成分分析方法。仿真试验结果表明主成分分析提取的图像特征明显优于使用Hu矩和伪Zernike矩等方法的不变矩图像特征,同时自适应主成分分析方法能有效避免特征的冗余或缺失的情况。
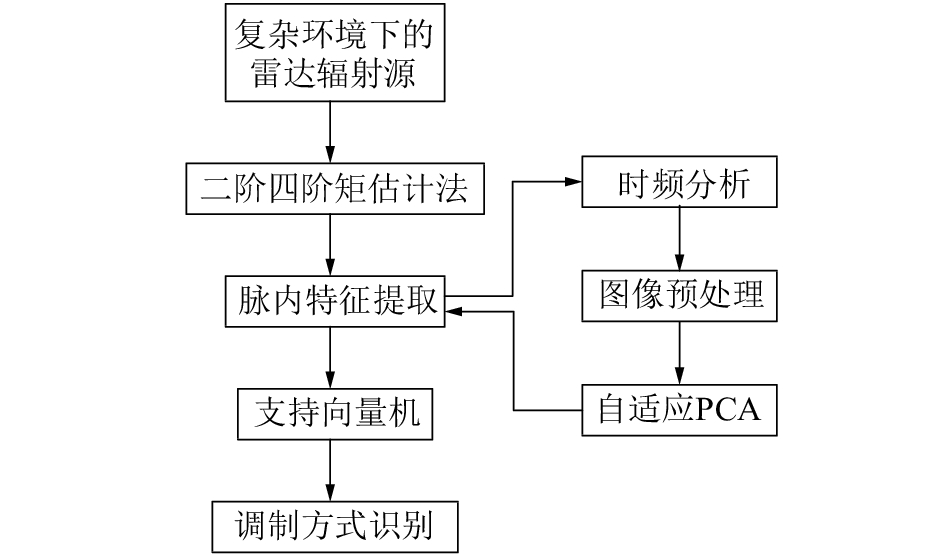
1 系统模型雷达信号调制识别系统模型如图 1所示。
|
Download:
|
| 图 1 系统模型 | |
首先,由接收端得到雷达信号后,对其进行时频分析,将雷达信号从时域信号转换为时间–频率二维时频图像;然后使用图像处理技术降低计算复杂度和特征维数,经过灰度化、图像归一化、二值化、形态学处理等图像预处理操作,增强信号特征信息在图像中的比重;随后,联合二阶四阶矩估计方法,利用自适应主成分分析算法,对预处理后的图像进行图像形状特征提取;最后,结合支持向量机分类器,识别出雷达信号的调制方式。
2 辐射源调制识别 2.1 时频分析Wigner-Ville分布描述了信号的瞬时自相关函数经过傅里叶变换到时频域上的能量分布。Cohen用一个统一形式来表示一个信号z(t)的时频分布,即
| $\begin{aligned}P\left( {t, \omega } \right) = & \displaystyle\frac{1}{{2\pi }}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {z\left( {\mu + \frac{{\rm{ \mathsf{ \tau} }}}{2}} \right)} } } {z^*}\left( {\mu - \frac{{\rm{ \mathsf{ \tau} }}}{2}} \right) \cdot \\& \;\phi \left( {{\rm{ \mathsf{ \tau} }}, \xi } \right){{\rm{e}}^{ - {\rm{j}}\left( {t\xi + {\rm{ \mathsf{ \tau} }}f - \xi \mu } \right)}}{\rm{d}}\mu {\rm{d \mathsf{ \tau} d}}\xi =\\ & \displaystyle\frac{1}{{2\pi }}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{\chi _z}} } \left( {{\rm{ \mathsf{ \tau} }}, \xi } \right)\phi \left( {{\rm{ \mathsf{ \tau} }}, \xi } \right){{\rm{e}}^{ - {\rm{j}}\left( {t\xi + {\rm{ \mathsf{ \tau} }}\omega } \right)}}{\rm{d \mathsf{ \tau} d}}\xi \end{aligned}$ |
式中:
| $\begin{array}{*{20}{l}}{{W_{{\rm{CWD}}}}\left( {t,\omega } \right) = \int_{ - \infty }^\infty {{{\rm{e}}^{ - {\rm{j}}\omega {\rm{ \mathsf{ \tau} }}}}} \Biggl[\int_{ - \infty }^\infty \displaystyle{\sqrt {\frac{\sigma }{{4\pi {{\rm{ \mathsf{ \tau} }}^2}}}} z\left( {\mu + \frac{{\rm{ \mathsf{ \tau} }}}{2}} \right) \cdot } }\\{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{z^*}\left( {\mu - \displaystyle\frac{{\rm{ \mathsf{ \tau} }}}{2}} \right){{\rm{e}}^{ - \sigma {{\left( {\mu - t} \right)}^2}/4{{\rm{ \mathsf{ \tau} }}^2}}}{\rm{d}}\mu \Biggl]d{\rm{ \mathsf{\tau} }}}\end{array}$ | (1) |
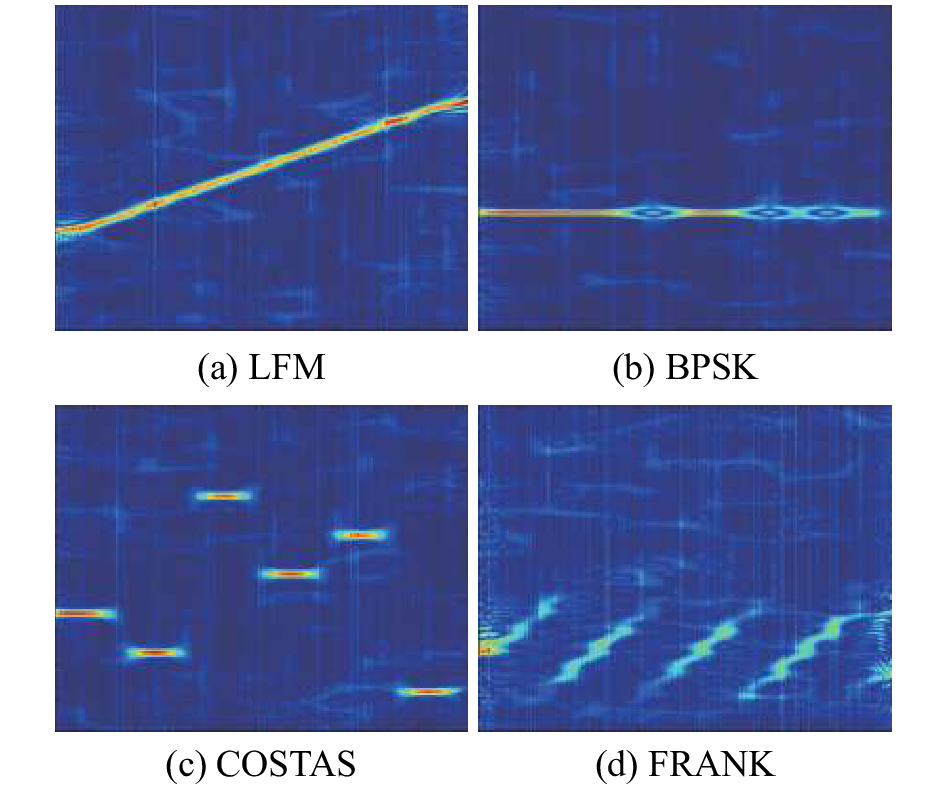
图 2是本文仿真时使用的时频图像,即4种雷达辐射源信号在信噪比为0 dB时使用Choi-Williams分布变换后得到的时频图像。时频图像直观反映了雷达辐射源信号的脉内调制信息,故可使用图像处理方法从时频图像中提取调制特征,进而实现雷达辐射源信号的调制识别。
|
Download:
|
| 图 2 4种雷达辐射源信号在信噪比为0 dB时的CWD时频图像 | |
时频分布CWD将雷达信号在时间和频率二维空间内联合表示,将时频图像经过预处理后,得到二值图像可以很好地表征时频图像的骨架特征。利用主成分分析去掉样本的冗余信息留下代表样本的主要信息的成分,从而提取出时频图像的有用特征[10-12]。
将时频图像作为原始样本构成一个数据矩阵为
| ${{{ X}}_{M \times N}} = \left[ {\begin{array}{*{20}{c}}{{{{x}}_{11}}}&{{x_{12}}}& \cdots &{{x_{1N}}}\\{{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2N}}}\\ \vdots & \cdots & \cdots & \vdots \\{{x_{M1}}}&{{x_{M2}}}& \cdots &{{x_{MN}}}\end{array}} \right]$ | (2) |
其协方差矩阵为R=XXT,可对该协方差矩阵作特征值分解:
| ${{{R}}_{M \times M}} = {{U {\varLambda} }}{{{ U}}^{\rm{T}}}$ | (3) |
式中:T表示转置,Λ为协方差矩阵的特征值对角阵,U为相应的特征矩阵,对时频图像作如下变换:
| ${{{ P}}_{M \times N}} = {{{U}}^{\rm{T}}}{{X}} = {\left[{{p_1}, {p_2}, \cdots, {p_M}} \right]^{\rm{T}}}$ | (4) |
式中:P为时频图像二值矩阵的主成分,p1是第一主成分,pj为第j主成分,选取前k个主成分,构成时频图像的骨架特征矩阵。
在不同的信噪比时,由于噪声的影响图片上的骨架特征会掺入杂质,而过多地提取高信噪比时的成分分量,会弱化了区分性能强的成分分量,导致性能下降。为解决上述问题而引入自适应主成分分析算法,以实现不同信噪比时选取不同的主成分分量。
2.3 二阶四阶矩估计法二阶四阶矩估计法是利用信号的二阶矩和四阶矩对信噪比进行估计的一种算法[13],假设接收到的信号为
x(n)二阶矩M2为
| ${M_2} = {\rm E}\left[{{x_n}x_n^*} \right] = {A^2} + {\sigma ^2}$ | (5) |
x(n)四阶矩M4为
| ${M_4} = {\rm E}\left[{{{\left( {{x_n}x_n^*} \right)}^2}} \right] = {A^4} + 2{\sigma ^4} + 4{A^2}{\sigma ^2}$ | (6) |
联立式(5)、(6),可解得A2、σ2的估计值为
| $\left\{\begin{aligned}&{{G}_{{{A}^{2}}}}=\sqrt{2M_{2}^{2}-{{M}_{4}}}\\ &{{H}_{{{\sigma }^{2}}}}={{M}_{2}}-\sqrt{2M_{2}^{2}-{{M}_{4}}}\end{aligned}\right.$ | (7) |
信噪比估计值NSNR可定义为
| ${N_{{\rm{SNR}}}} = \frac{{\sqrt {2M_2^2 - {M_4}} }}{{{M_2} - \sqrt {2M_2^2 - {M_4}} }}$ | (8) |
将信噪比估计法与主成分分析算法相结合,实现在不同信噪比下选取不同的主成分分量的自适应主成分分析算法。
2.4 支持向量机分类器支持向量机(support vector machine, SVM)是V.Vapnik提出的一种基于结构风险最小化,在特征空间中通过最大化分类间隔寻找最优分界面的分类方法[14-15]。该方法的核心思想就是通过非线性映射将输入向量变换到高维特征空间,在高维特征空间中构造最优分类超平面,并在高维特征空间中达到分类样本的目的。
在实际应用中,引入松弛变量
| ${\rm{min}}\left\{ {\frac{1}{2}{w^*}w + \sum\limits_{i = 1}^n {{\xi _i}} } \right\}$ |
为求解上述优化问题,引入拉格朗日函数L:
| $\begin{array}{l}L\left( {w, b, {\xi _i}, {\alpha _i}, {\lambda _i}} \right) = \displaystyle\frac{1}{2}{w^*}w + C\sum\limits_{i = 1}^n {{\xi _i}} - \sum\limits_{i = 1}^n {{\lambda _i}{\xi _i}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\displaystyle\sum\limits_{i = 1}^n {{\alpha _i}\left[{{y_i}\left( {{w_i} \cdot \varphi \left( {{x_i}} \right) + b} \right)-1 + {\xi _i}} \right]} \\ \end{array}$ |
式中C称为惩罚因子。约束最优化问题的解由拉格朗日函数的鞍点决定,并且最优化问题的解在鞍点处满足对w,b和
| $\max \left( {a{}_i} \right) = \sum\limits_{i = 1}^n {{\alpha _i}} - \frac{1}{2}\sum\limits_{i, j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}K({x_i} \cdot {x_j})} $ |
式中
| $f(x) = {\rm{sgn}}\left[{\sum\limits_{i = 1}^n {{\alpha _i}{y_i}K({x_i} \cdot {x_j})} + b} \right]$ |
选用合适的核函数
本文采用基于标准支持向量机(criterion support vector machine, C-SVM),并选用具有适合处理非线性样本、计算模型简单、泛化性能优秀的径向基核函数。在选定径向基核函数SVM后,核函数参数σ和支持向量机惩罚因子C的选择对SVM性能起决定作用。过大的C导致较少的训练错误分类,从而使分类器在训练阶段获得较高的准确率和在测试阶段非常低的识别率;而过小的C则会出现更多的训练错误分类,将导致分类器的分类准确率不尽人意,即训练得出的模型没有实际应用价值。而核函数参数σ的选择值极大时将导致过拟合,而过小时则导致拟合不足,这2种情况都会使得分类器模型实际应用价值过低。因此在进行参数选择时必须同时兼顾C和σ,本文选用网格搜索法[16]对(C,σ)2个参数寻优。
2.5 调制识别具体步骤基于时频分析的自适应PCA辐射源调制信号调制识别步骤如下:
1)将辐射源信号代入式(5)~(8),估计得到信号在高斯白噪声下的信噪比。
2)将辐射源信号代入式(1),得到雷达辐射源信号的时频图像。
3)对时频图像使用灰度化、图像归一化、二值化、形态学处理等方法进行预处理,滤除冗余信息,增强有用特征。
4)利用主成分分析算法对预处理后图像提取信号特征,使用式(2)~(4)提取预处理后图像数据矩阵XM×N得到信号时频图像的骨架特征矩阵,自适应主成分分析算法依据步骤1)所得信噪比提取不同数量的主成分分量特征。
5)所有信号样本重复步骤1)~4),得到对应信噪比条件下的辐射源调制信号的样本特征数据集。
6) 将样本特征数据集的70%作为训练集,输入支持向量机,使用网格搜索法对(C,σ)2个参数寻优,以最优的(C,σ)为参数训练SVM得到分类器。
7) 将样本特征数据集的30%作为测试集,将其输入训练后的SVM分类器,进行信号调制识别。
3 仿真结果分析在MATLAB环境下对不同信噪比下的自适应主成分分析算法进行仿真分析。
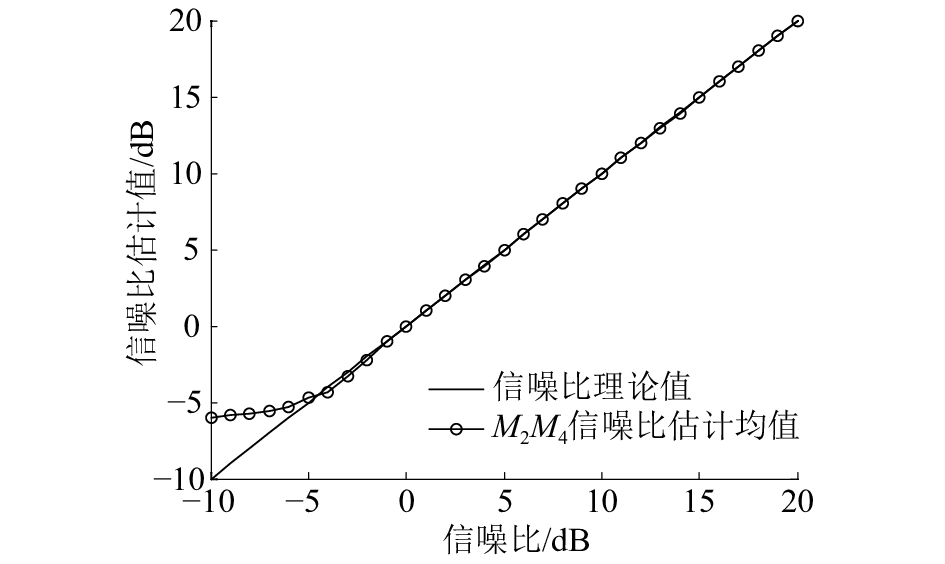
试验1 对本文所采用的二阶四阶矩估计法进行性能仿真,以较为常见的AWGN信道为例,选取调制方式为BPSK的信号进行信噪比估计仿真。待估计信噪比范围设为[–10, 20] dB,得到二阶、四阶矩估计法的信噪比估计均值,实验结果如图 3所示。
|
Download:
|
| 图 3 二阶四阶矩估计信噪比均值 | |
仿真结果表明:该估计算法在整个信噪比估计范围中性能良好,只是在信噪比低于–5 dB时性能有所下降。该估计算法不需要载波的相位信息,不需要进行接收判决,具有运算复杂度相对较小的优势。因此,在该应用场合下,二阶四阶矩估计法能很好的满足要求。
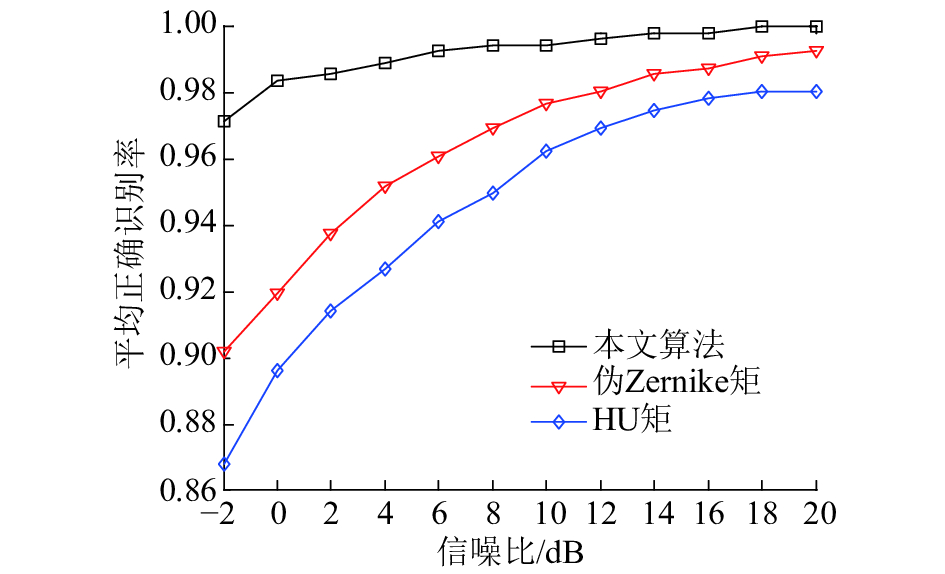
试验2 本文对LFM、BPSK、COSTAS、FRANK等4种调制方式的雷达辐射源信号进行仿真来验证本文算法的识别效果。其中载频为20 MHz,采样频率为100 MHz,脉冲宽度为10 μs,BPSK为7位Barker码。对于每一种待分类信号,在信噪比为–2~20 dB,每隔2 dB进行仿真试验,每种信号在当前信噪比下产生200个样本,其中每个信号随机选取140个样本进行SVM的训练,剩余的60个样本用于SVM分类器识别率的测试。同时也绘制了基于本文提出的PCA-10、PCA-15、PCA-20及自适应PCA图像特征提取方法和文献[7]提出的HU矩、伪Zernike矩图像特征提取方法,共6种不同特征提取情况下的SVM识别率变化曲线,得到的实验结果分别如图 4、5所示。

|
Download:
|
| 图 4 自适应PCA及不同PCA特征提取识别结果 | |
|
Download:
|
| 图 5 自适应PCA及不变矩特征提取识别结果 | |
仿真结果表明,在使用相同结构的SVM分类器情况下,基于PCA提取的图像特征、基于Hu矩提取的图像特征和基于伪Zernike矩提取的图像特征在信噪比大于0 dB的条件下识别效果均较好,基本达到了90%以上。但是另外2种特征提取方法识别率明显低于基于PCA的特征提取方法。同时,使用主成分分量特征越多,识别率越高,自适应PCA特征提取的识别率在各个信噪比情况下都有较高的识别率,信噪比–2 dB时达到了97%以上。由于Hu矩和伪Zernike矩都是提取图像中的不变矩特征,将不变矩特征应用于基于时频分析的信号调制识别中,得到的识别效果明显弱于基于PCA图像特征的调制识别。PCA-15和PCA-20相比,在高信噪比情况下选用PCA-20明显出现了特征冗余,PCA-10、PCA-15、PCA-20相比,在低信噪比情况下选用PCA-10、PCA-15明显出现了特征缺失,基于信噪比的自适应PCA特征提取实现了在对应信噪比选取合适数量的PCA特征,达到了较高的识别率。
4 结论本文提出了一种基于不同信噪比自适应提取PCA特征的调制识别新方法。
1)主成分分析算法相较于Hu矩和伪Zernike矩特征提取算法,提取雷达辐射源信号的时频图像特征能够更准确有效地应用于雷达信号调制识别。
2)将二阶四阶矩估计法与自适应PCA算法相结合,实现了在不同信噪比情况下提取不同数量的主成分分量特征。
3)自适应PCA特征提取的识别率在各个信噪比情况下都有较高的识别率,信噪比–2 dB时达到了97%以上。
4)该方法在信噪比越高时需要的主成分分量特征数越少,能够在适应不同的信噪比情况下,提升识别准确率,减少运算复杂度,具有较高的工程实践应用价值。
下一步将引入更多的图像特征提取方法,识别更多种类的雷达辐射源调制方式。
| [1] |
ZHANG Zhenyu, HUA Zhong, LIU Yingzhe. Modulation classification in multipath fading channels using sixth-order cumulants and stacked convolutional auto-encoders[J]. IET communications, 2017, 11(6): 910-915. DOI:10.1049/iet-com.2016.0533 ( 0) 0)
|
| [2] |
王静, 彭华. 多分量压缩感知信号调制参数估计算法[J]. 信息工程大学学报, 2013, 14(2): 189-195. DOI:10.3969/j.issn.1671-0673.2013.02.012 ( 0) 0)
|
| [3] |
FONTES A I R, PASA L A, DE SOUSA JR V A, et al. Automatic modulation classification using information theoretic similarity measures[C]//Proceedings of 2012 IEEE Vehicular Technology Conference. Quebec City, Canada, 2012: 1-5.
( 0) 0)
|
| [4] |
CAI Tian, WANG Cheng, CUI Gaofeng, et al. Constellation-wavelet transform automatic modulation identifier for M-ary QAM signals[C]//Proceedings of 2015 IEEE Annual International Symposium on Personal, Indoor, and Mobile Radio Communications. Hong Kong, China, 2015: 212-216.
( 0) 0)
|
| [5] |
LI Qiang, SHEN Dong, WANG Fei. MQAM modulation recognition based on AP clustering method[C]// Proceedings of 2016 International Conference on Electronic, Information and Computer Engineering. Lanzhou, China, 2016, 44: 01002.
( 0) 0)
|
| [6] |
熊坤来, 罗景青, 吴世龙. 基于时频图像和神经网络的LPI雷达信号调制识别[J]. 弹箭与制导学报, 2011, 31(5): 230-233. DOI:10.3969/j.issn.1673-9728.2011.05.066 ( 0) 0)
|
| [7] |
白航, 赵拥军, 胡德秀, 等. 基于Choi-Williams时频图像特征的雷达辐射源识别[J]. 数据采集与处理, 2012, 27(4): 480-485. DOI:10.3969/j.issn.1004-9037.2012.04.014 ( 0) 0)
|
| [8] |
TAVAKOLI E T, FALAHATI A. Radar Signal Recognition by CWD Picture Features[J]. International journal of communications, network and system sciences, 2012, 5(4): 238-242. DOI:10.4236/ijcns.2012.54031 ( 0) 0)
|
| [9] |
LIU Yongjian, XIAO Peng, WU Hongchao, et al. LPI radar signal detection based on radial integration of Choi-Williams time-frequency image[J]. Journal of systems engineering and electronics, 2015, 26(5): 973-981. DOI:10.1109/JSEE.2015.00106 ( 0) 0)
|
| [10] |
BALSUBRAMANI A, DASGUPTA S, FREUND Y. The fast convergence of incremental PCA[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada, 2015, 2: 3174-3182.
( 0) 0)
|
| [11] |
孙岩, 赵春晖, 江凌. 基于NSCT和PCA变换域的遥感图像融合算法[J]. 沈阳工业大学学报, 2011, 33(3): 308-314. ( 0) 0)
|
| [12] |
于洋, 梁佳鑫, 李孟格. 标准化HU不变矩算法的车脸图像特征提取[J]. 沈阳理工大学学报, 2016, 35(6): 72-76. DOI:10.3969/j.issn.1003-1251.2016.06.014 ( 0) 0)
|
| [13] |
王维平, 胡国兵. M2M4信噪比估计算法的统计性能分析[J]. 现代雷达, 2012, 34(8): 42-45. DOI:10.3969/j.issn.1004-7859.2012.08.009 ( 0) 0)
|
| [14] |
魏峻. 一种有效的支持向量机参数优化算法[J]. 计算机技术与发展, 2015, 25(12): 97-100. ( 0) 0)
|
| [15] |
梁礼明, 钟震, 陈召阳. 支持向量机核函数选择研究与仿真[J]. 计算机工程与科学, 2015, 37(6): 1135-1141. DOI:10.3969/j.issn.1007-130X.2015.06.015 ( 0) 0)
|
| [16] |
罗小燕, 陈慧明, 卢小江, 等. 基于网格搜索与交叉验证的SVM磨机负荷预测[J]. 中国测试, 2017, 43(1): 132-135, 144. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


