超声诊断是生物医学中一个活跃而有广阔前景的分支，它根据超声波在人体的传播过程中与组织的相互作用，包括信号的衰减、反射及透射等，从接收信号中提取能够反映组织状况的信息，加以处理显示，对生物组织的结构特性及质量进行无损评估。常见的超声诊断通常采用反射法，实际上回波是一种不确定信号，高质量的信号分析不能仅使用反射数据重建^[1]。与回波信号相比，透射信号受到的组织内的随机因素影响较小，其幅值的变化遵循生物组织的超声衰减规律，可以作为一种确定性信号，结果比较精确。

声衰减代表超声波通过生物组织的能量损失，是组织测量的一种基本属性，传达着关于组织成分的重要信息，在医学诊断中起重要作用。基于衰减特征的信号测量有两个主要类别：一种是研究时域信号的幅度^[2-3]，另一种是研究频域信号的频谱含量^[4-5]。超声时域检测可以获得超声在软组织中的时间延迟、声速等信息，频域检测能更好地表现生物组织的衰减特性随超声频率的变化情况以及相位信息等。本文重点在于研究比较超声时频信号对于生物组织结构变化的敏感情况，可以更好地区分、检测生物组织的结构变化，提高超声检测的精确性。

本文分别采用最大值法^[6]与能量比较法^[7]对超声时频域信号进行采集与比较。最大值法简便直观，缺点是受随机因素影响大，能量比较法相对于最大值法，在随机因素的影响下表现比较稳定。

1 超声传播模型 1.1 传播衰减

超声在生物组织中传播会发生能量损失。衰减系数可以用来预测组织内超声波束的吸收和散射行为，通过信号衰减的程度推测生物组织的状态信息^[8]。

超声衰减通常被近似为频率的幂函数^[9]:

$\alpha (f) = {\alpha _0}{(f/{f_0})^n}$

式中： ${\alpha _0}$ 为频率 ${f_0}$ 时的衰减系数， $n$ 为衰减的频率依赖指数。当 $n = 1$ 时,衰减系数成为频率的线性函数。

生物组织对超声的衰减作用可以表示为位置和时间的传递函数 $h(r,t)$ ：

$h(r,t) = \sum\limits_{i = 1}^N {{A_i}(t)} \delta (t - {\tau _i})$

式中： ${A_i} = \exp ( - \alpha (f)c{\tau _i})$ ， $c$ 为组织的声速， ${A_i}(t)$ 、 ${\tau _i}$ 分别表示超声在组织 $i$ 位置处的信号幅值与时间延迟，超声的传播距离为 $d = c{\tau _i}$ 。

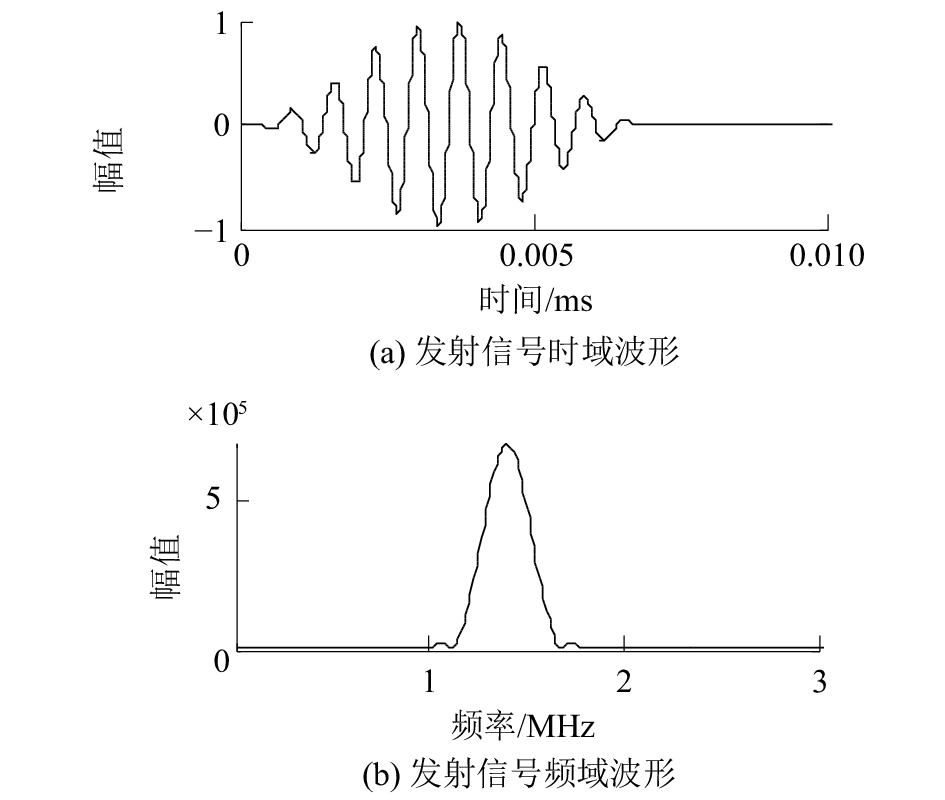
生物组织作为信道，发射信号（图1）选取汉宁窗调制的正弦叠加信号，其表达式为

$x(t) = [1 - \cos (\frac{{2{\rm{\pi }} \cdot {f_0} \cdot t}}{m})] \cdot \sin (2{\rm{\pi }} \cdot {f_0} \cdot t)$

式中： $m$ 表示单音频的个数，本实验中 $m = 5$ ； ${f_0}$ 为信号的中心频率， ${f_0} = 1.4 \;{\rm{MHz}}$ 。本文采用汉宁窗作为调制函数，可以使信号能量更多的集中在主瓣附近，使得信号的识别度高。

人体软组织看作为线性卷积系统，传递响应函数的实际作用可以表示为对时域的周期性传递和对频域的抽样性传递关系。输入、输出的时频域关系表达式为

$s(r,t) = x(t)h(r,t)$

(1)

$S(w) = X(w)H(w) = X(w)\exp ( - \alpha (f)d)$

(2)

1.2 分层组织

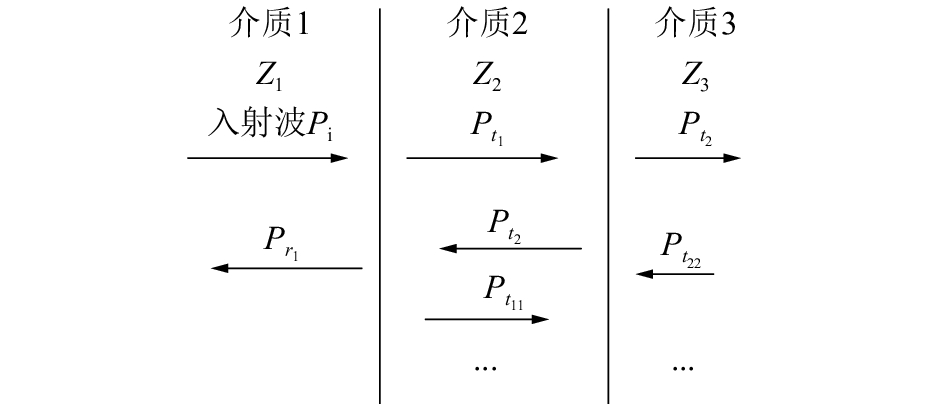
如果生物组织是单一均匀介质，我们可以直接利用式(1)、(2)进行测量。当超声遇到分层介质，且介质可以看做流体的情况下，超声是可以在分层介质间传播的，并且波形不发生改变^[10]。超声在非单一结构的生物组织中传播，除了各介质的衰减系数不同外，由于相邻介质声阻抗的不匹配，会使超声能量在界面处发生变化，如图2所示，一部分声能量遇界面返回形成反射波，另一部分声能量经过界面形成透射波^[8]。

界面处的能量分配通常用透射系数 ${t_p}$ 和反射系数 ${r_p}$ 来表示。透射系数和反射系数的大小取决于相邻介质的声特性阻抗值 $z$ , $z = \rho c$ , $\rho $ 、 $c$ 分别为组织的密度和声速。图2中介质1的声特性阻抗 ${z_1} = {\rho _1}{c_1}$ ,介质2的声特性阻抗 ${z_2} = {\rho _2}{c_2}$ ，介质3的声特性阻抗 ${z_3} = {\rho _3}{c_3}$ 。由介质1到介质2的透射系数 ${t_{{p_{_2}}}}$ 和由介质2到介质3的透射系数 ${t_{{p_2}}}$ 分别为

${t_{{p_{_{1}}}}} = \frac{{{p_{{t_1}}}}}{{{p_i}}} = \frac{{2{z_2}}}{{{z_1} + {z_2}}}$

${t_{{p_{_{2}}}}} = \frac{{{p_{{t_2}}}}}{{{p_{{t_1}}}}} = \frac{{2{z_3}}}{{{z_2} + {z_3}}}$

2 信号测量 2.1 最大值法

超声经过生物组织的传递响应作用，信号会随着时间和频率发生变化，在汉宁窗函数的调制作用下，时域信号和频域信号都会存在一个最大值点，通过采集不同响应作用下的信号最大值点，可以直观地表示组织微结构变化对超声信号带来的影响。时域和频域信号的最大值点可以表示为

$I(t) = \max \{ \left| {s(t)} \right|\} $

$J(\omega ) = \max \{ \left| {S(\omega )} \right|\} $

文中我们会设置不同的组织样本，组织成分每变化一次，采集一次信号，通过最大值法采集到的不同组织样本的时域、频域接收信号为

$A = \left[ {{I_1}(t),{I_2}(t),{I_3}(t),{I_4}(t), \cdots \cdots } \right]$

$B = \left[ {{J_1}(\omega ),{J_2}(\omega ),{J_3}(\omega ),{J_4}(\omega ), \cdots \cdots } \right]$

将第N次采集信号与第N−1次采集信号对比，用来表示最大值法在组织样本变化下对信号变化的识别度，若 $\max \{ \left| {{s_N}(t)} \right|\} > \max \{ \left| {{s_{N - 1}}(t)} \right|\} $ ，则

${n_{N - 1}} = \frac{{\max \{ \left| {{s_N}(t)} \right|\} - \max \{ \left| {{s_{N - 1}}(t)} \right|}}{{\max \{ \left| {{s_N}(t)} \right|\} }}$

否则

${n_{N - 1}} = \frac{{\max \{ \left| {{s_{N - 1}}(t)} \right|\} - \max \{ \left| {{s_N}(t)} \right|}}{{\max \{ \left| {{s_{N - 1}}(t)} \right|\} }}$

频域信号也是一样处理，从而得到新的时域、频域信号数组：

$N = \left[ {{n_1},{n_2},{n_3},{n_4}, \cdots \cdots } \right]$

$M = \left[ {{m_1},{m_2},{m_3},{m_4}, \cdots \cdots } \right]$

2.2 能量比较法

最大值法可以简单、直观地描述生物组织介质变化下信号的幅值衰落，缺点是受随机因素影响大、不稳定。能量比较法取决于信号的整体能量，在外界因素影响下，信号变化稳定、可靠。比较2种方法对时频域信号变化的敏感度。能量比较法通过捕获时间窗 $[{t_1},{t_2}]$ 内的超声波能量对超声时域衰减信号进行测量

$E(t) = {\int_{{t_1}}^{{t_2}} {s(t)} ^2}{\rm{d}}t$

同理，捕获频域 $[{w_1},{w_2}]$ 内的频谱能量：

$E(w) = {\int_{{w_1}}^{{w_2}} {S(w)} ^2}{\rm{d}}w$

通过能量比较法采集到的组织样本变化下的时域、频域接收信号为

$C = \left[ {{E_1}(t),{E_2}(t),{E_3}(t),{E_4}(t), \cdots \cdots } \right]$

$D = \left[ {{E_1}(w),{E_2}(w),{E_3}(w),{E_4}(w), \cdots \cdots } \right]$

将采集信号进行对比处理，得到新的时域、频域信号数组：

$P = \left[ {{p_1},{p_2},{p_3},{p_4}, \cdots \cdots } \right]$

$Q = \left[ {{q_1},{q_2},{q_3},{q_4}, \cdots \cdots } \right]$

3 仿真实验

为了保证仿真实验结果的可靠性、有效性，选取合理有依据的生物组织特性参数值^[11-12]，同时设置单层、双层、三层的生物组织样本，样本的选择应遵循数量、种类尽可能多的原则，为了在文中清楚地描述信号随组织特性的变化，每种样本取10组数据。

3.1 单层组织

单层组织的参数设置如表1所示，组织样本具有相同的厚度，不同的组织成分。

在组织厚度相同，组织成分不同的条件下，超声时域、频域接收信号随组织成分变化的情况如图3所示。

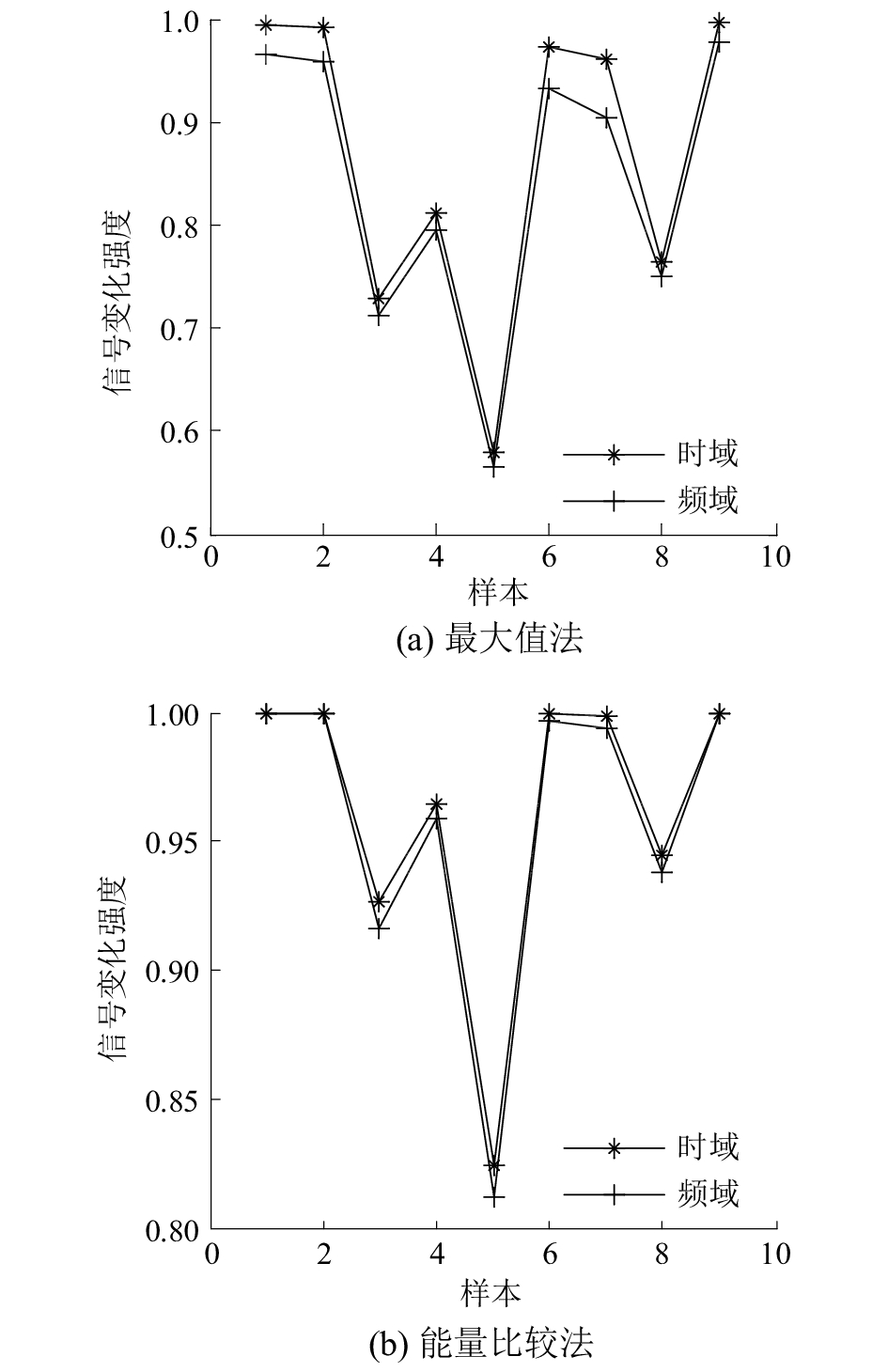
为了使仿真结果清晰、便于观察，选取时域、频域接收信号的前4组展示。从图3可以看出，当组织样本成分不同时，接收信号的时间延迟是不一样的，信号衰减程度也不同。相对来说，样本1衰减程度小，样本2信号衰减严重，根据接收信号的时间延迟和衰落程度可以对组织的厚度和成分进行推断。时域、频域接收信号存在最大值点，采集接收信号的最大值点进行处理得到N、M数组，如图4（a）所示；对接收信号的能量进行处理得到P、Q数组，如图4（b）所示。

从图4可以看出，不管采用最大值法还是能量比较法对接收信号比较，当组织成分发生变化时，不同样本之间时域接收信号的变化强度更高，信号差异性更大，频域信号之间的差异性小一些。表明时域信号对于组织成分的变化更敏感，随组织成分变化程度更强，对组织微结构的识别性更高。为了验证这一结论，我们再用同样的方法对双层、三层组织样本进行检测。

3.2 双层组织

双层组织的参数设置如表2所示，组织具有相同的厚度，不同的组织分布。考虑到信号发射频率可能对实验结果产生影响，基于超声探头频率多为1~5 MHz，本节发射信号的中心频率 ${f_0}$ 分别选取1.4、2、3、4 MHz。

发射频率为1.4 MHz的前4组时域、频域接收信号如图5所示，其他发射频率的接收信号波形与图5相似。超声经过双层组织的时间延迟及衰落如图5(a)所示，信号随频率的衰落如图5(b)所示。

当生物组织成分不同时接收信号的差异还是很大的。在组织类型不同的情况下，信号发生不同的时延和衰减。对双层组织的时频域接收信号进行最大值法和能量法采样处理，得到各发射频率下时频域信号随组织成分变化的示意图如图6所示。

通过图6可看出，在不同的发射频率下，尽管部分信号变化相重叠，无论最大值法还是能量法都表明，时域信号随组织成分的变化幅度高于频域信号。同时可以看出，最大值法中信号的波动幅度较大，能量比较法平稳些，相对于同一样本的信号变化检测，能量比较法一直高于最大值法。由此可见，最大值法波动较大，对于信号测量不稳定，且对于信号变化的检测识别低于能量比较法。

3.3 三层组织

三层组织的参数设置如表3所示。实际超声测量中会存在噪声干扰，本节分别对理想样本和加噪样本的接收信号进行处理比较，证明实验结果的有效性。

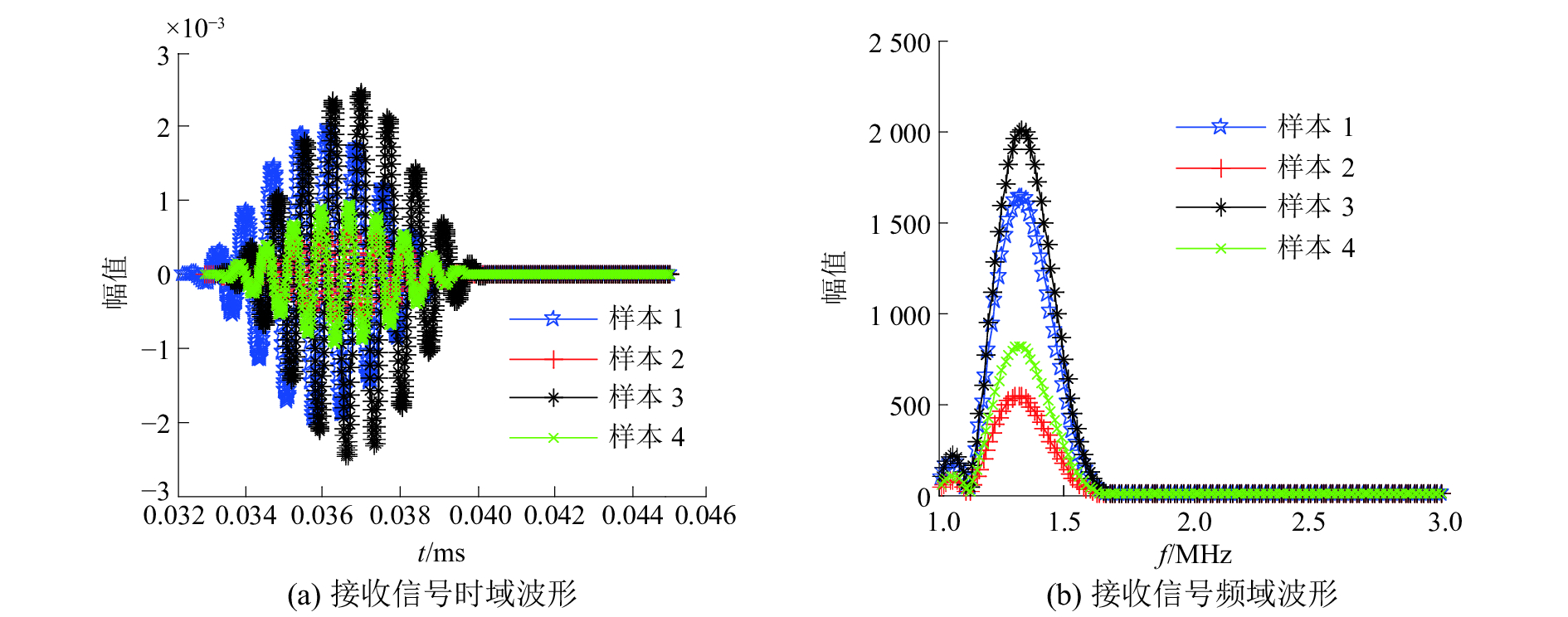
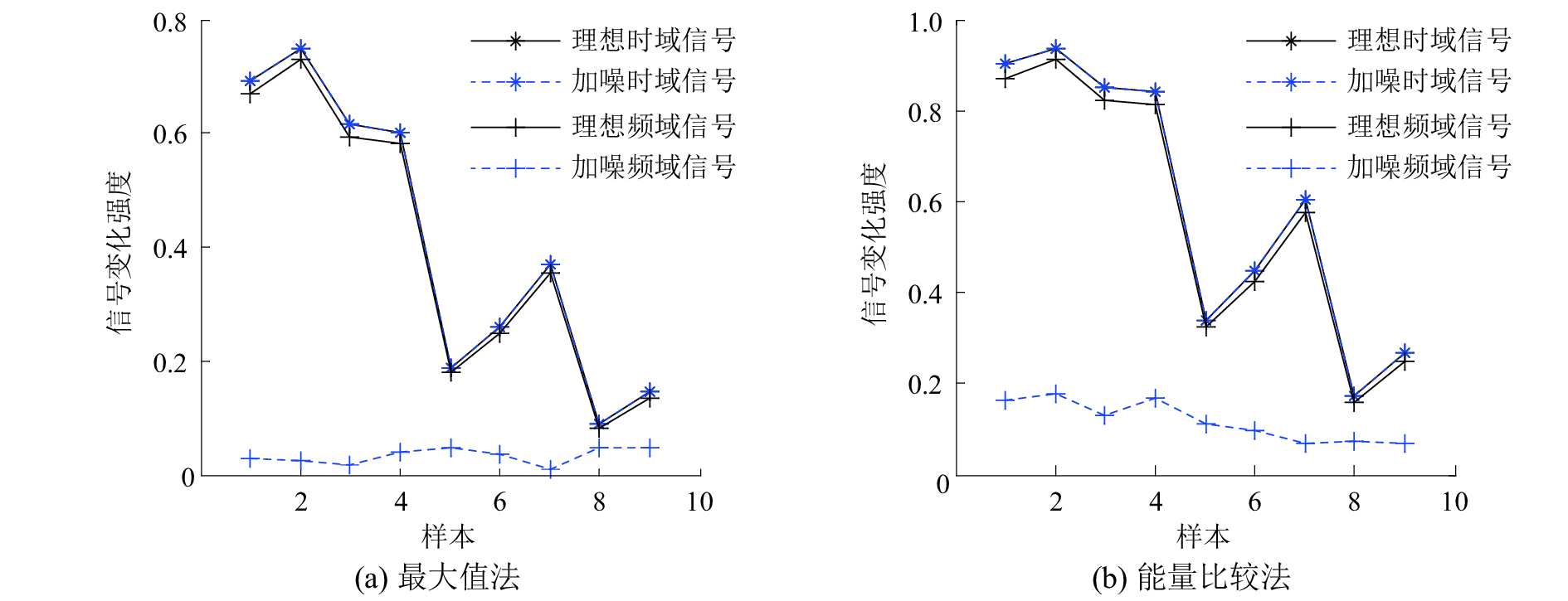
三层组织的前4组时域、频域接收信号如图7所示，加噪样本的接收信号只处理不显示。通过图7可以看出，当组织厚度不变，组织成分发生变化时，接收信号的幅值衰落和时间延迟是不一样的，根据接收信号的变化可以对组织成分和病理状态进行分析。对接收信号采用最大值法和能量比较法进行处理，得到超声信号随组织成分变化的示意图如图8所示。加噪样本和理想的时频域信号变化出现了部分重合，通过图8仍可以清晰地显示，理想和加噪样本的时域接收信号随组织成分的变化强度始终高于频域信号。时域信号对组织微结构变化更敏感，所以采用时域信号对组织的成分或病理状态检测效果更好，精度更高。最大值法和能量法都能对信号变化进行识别，相对来说，能量比较法对信号变化检测更稳定，同一样本条件下信号的变化识别度也高于最大值法，同时能量比较法受客观因素影响较小，因此能量比较法更适合于对信号变化的检测识别。

4 结论

1）本文针对生物组织微结构成分的信号检测问题，采用时域、频域信号检测对比分析，目的是为了比较两者对于组织成分变化的敏感程度。

2）对接收信号进行比较，涉及到信号的提取问题，本文采用简便直观的最大值法和稳定的能量比较法对信号进行提取比较。结果表明，当生物组织成分发生变化时，时域信号的变化程度更强，对组织微结构变化识别度更高，有利于识别组织异变等变化。

3）最大值法与能量法相比较，能量比较法对于信号的测量更稳定，对信号变化感知度更强，有利于反映信号的异常变化。

3）同时，最大值法与能量法相比较，能量比较法对于信号的测量更稳定，对信号变化感知度更强，有利于反映信号的异常变化。

4）根据时域信号在检测精度方面的价值，在生物组织的超声诊断中，采用时域信号对组织病变进行检测，能量比较法对信号进行测量，利用超声在病变信号与正常组织信号的差异，形成能量灰度不同的图像，提高超声诊断的准确性。