2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China
声散射现象在现实生活当中随处可见,对其内在机理的研究早已得到了各国学者的关注,从而在理论研究领域发展出了许多有关声散射的解析方法,诸如共振散射理论[1]、Sommerfeld-Watson变换法[2]等。众所周知,理论解析法一般只能适用于一些形状比较简单的物体,而对于形状结构更为复杂的物体,则出现了一些半解析半数值的方法承担着对其进行研究的任务,包括分波序列展开法(partial wave series expansion, PWSE)[3]、T矩阵法[4]、格林函数法[5]等。另外,随着计算机仿真技术的不断发展,有限元法(finite element method, FEM)[6-8]、边界元法[9]等数值方法依托计算软件以其适用性强的优势而得到了广泛的应用。除了上述的理论和数值的研究方法之外,学者们还使用过实验测量的方法对目标声散射进行研究,如声目标强度的直接测量法、应答器法等[10]。
正是由于有着大量的声散射研究成果,声目标强度作为物体重要的声散射特性才能够被广泛应用在海洋资源勘探、水下搜救与避碰、潜艇声隐身等诸多领域之中[11-12]。其中,潜艇作为保障国防安全的战略性武器,保证其作战安全性的一个重要方向就是提高其隐蔽性,而舵结构作为潜艇重要的结构之一,对其声散射特性的研究因而具有十分重要的现实意义。
本文采用有限元数值计算方法对复合材料舵结构的声目标强度进行计算分析,首先介绍了有限元法解声学问题的相应理论,然后以单层球壳模型对计算方法的有效性进行了验证,最后针对舵结构的正横目标强度、散射声压以及目标强度指向性进行了计算和分析。
1 声学有限元理论 1.1 有限元理论经典的有限元法来源于变分原理,是求解水下声学问题的一种十分重要且应用广泛的数值方法。求解声学问题时,给出了理想流体介质中的小振幅线性声学波动方程的Helmholtz方程,即
| ${\nabla ^2}p + {k^2}p = 0$ | (1) |
求解波动方程(1)需要给定合适的边界条件,诸如狄利克雷边界条件
| $\begin{array}{l}\int_\Omega {\nabla w \cdot \nabla p{\rm{d}}} \varOmega - {k^2}\int_\Omega {w \cdot p{\rm{d}}} \varOmega + {\rm{j}}\rho \omega \int_{{\varGamma _N}} {w{v_n}{\rm{d}}} \varGamma + \\{\rm{j}}\rho \omega {A_n}\int_{{\varGamma _R}} {wp{\rm{d}}\varGamma {\rm{ = 0}}} \end{array}$ | (2) |
式中:
对于一般的声学问题,推导有限元法的计算模型首先需要将声学域
| $p(r) = \sum\limits_{i = 1}^n {{N_i}(r){p_i} = N(r)p} $ | (3) |
式中:n为所划分的有限元网格的节点数,
| $\left[ {{K} - {k^2}{M} + {\rm{j}}\rho \omega {C}} \right]{p} = - {\rm{j}}\rho \omega {F}$ | (4) |
式中:K、M、C和F分别表示声学刚度矩阵,声学质量矩阵,声学阻尼矩阵和声学节点力向量。利用声学有限元法对声学问题进行求解时,即为对式(4)的求解。
1.2 自动匹配层(automatically matched layer, AML)技术理论上,只要将计算所需的网格划分得足够精细,有限元法是能够有效而准确地求解声学问题的。但是对于无限域,实际上无法利用有限单元对其进行模拟,声学有限元法不适用。然而,正是由于有限元法对求解无限域中的声学问题的无能为力,完美匹配层(perfectly matched layer, PML)技术应运而生,而AML技术则是第十版本的LMS Virtual Lab声学计算软件中开发出的对PML方法的优化方法,其理论框架来自于PML方法。相比于早期出现的无限元技术,PML方法更具实用性,PML层除了必须是凸面轮廓之外没有其他的外形约束,并可以做到很薄而大大降低网格数量。而AML方法不需要像PML方法一样人为地画出吸收层网格,只需定义声学有限元辐射边界,软件会自动根据物理模型定义吸收层和吸收系数[13]。
在实际的软件操作中,AML法只要求画出很薄的包络结构的水域体网格,并将水域网格的最外层单元设置为AML属性即可,计算时求解器会自动建立吸声层来模拟无反射边界,极大地简化了建模和计算工作。另外,AML技术能够广泛适用于声散射、外部辐射噪声、管道声学等领域,并且极大地提高了计算精度和计算效率。然而,AML法也存在一定的限制,其一是软件中只允许存在一个AML属性,即设置对象是唯一的,而不能同时对多个对象进行AML属性设置;其二是设置了AML属性后不能进行模态计算和瞬态时域分析。
2 计算流程及验证 2.1 计算流程本文利用LMS Virtual Lab声学软件进行声散射的计算,采用的是有限元法来求解水下声散射问题,并应用AML技术来处理无限水域的边界问题,从而能够最终实现目标强度的计算。首先是模型的建立,对结构来说,需要将计算模型的几何结构进行建模,然后将几何模型进行网格的划分和材料属性的设置;对声学介质来说,仅需将包络结构的水域以设置了介质物理属性(ρ=1 025 kg/m3、c=1 500 m/s)的体网格建立出来即可。然后是声学响应计算,本文皆采用平面波作为入射波,定义远场收发合置的计算场点对散射声压进行计算,并利用球面扩展定律将声压折算到距离目标声学中心1 m处。最后,将上述得到的散射声压进一步计算平面波入射下结构的声散射目标强度,传统的远场收发合置的目标强度公式为
| ${T_S} = 20{\log _{10}}\frac{{{P_r}}}{{{P_i}}}\left| {_{r = 1}} \right.$ |
式中:
为了验证本文采用的结合AML技术的有限元法的有效性,本文将分波序列法计算的目标强度的结果作为参照对比。验证模型为浸没在无限水域中的内部为真空的单层钢质球壳,其半径为1.0 m,厚度为0.03 m,材料密度为7 850 kg/m3,杨氏模量为210 GPa,泊松比为0.3,纵波速度为5 950 m/s,横波速度为3 240 m/s。在有限元法的计算中,网格模型按照最高计算频率所对应的单个波长内至少有6个单元的原则建立(λ/6准则)。单层球壳的验证模型以壳单元建立,网格尺寸30 mm,如图 1所示。

|
Download:
|
| 图 1 单层球壳有限元模型 | |
计算结果如图 2所示,与分波序列法计算的解析解比较,在频率低于6 kHz时,有限元法计算的结果十分接近,有着较高的准确度;然而,在更高的频率段内,有限元法的结果不仅在峰值频率上相差较大,也在目标强度的数值上有着较大的出入。由于有限元法对高频计算不准确的缺陷,即使遵循上述网格划分原则后依然如此,因此,在以下舵结构的声散射计算中将最高计算频率设置在6 kHz,并仍按照λ/6准则建立网格。

|
Download:
|
| 图 2 有限元法和分波序列法计算的单层球壳的目标强度 | |
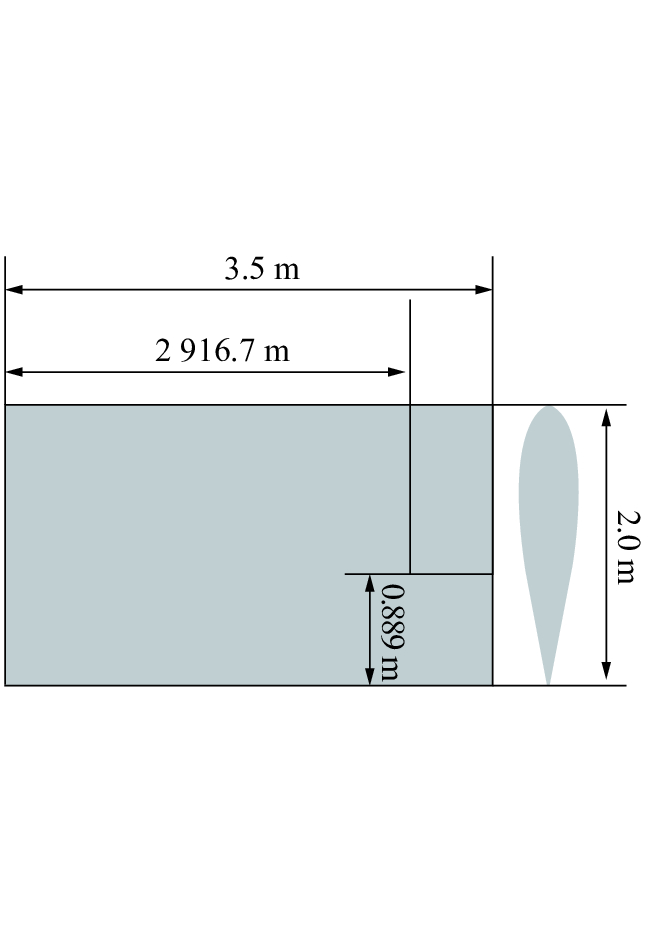
本文研究对象为水下航行体的舵翼结构,其横剖面线型为标准的NACA0021翼型,此翼型有着固定的尺寸系数,舵结构模型的主要尺寸如图 3所示。
|
Download:
|
| 图 3 舵结构的几何外形 | |
为了深入研究复合材料对舵结构声散射的影响,本文将钢质舵作为参照进行声散射特性的对比分析。上述2种舵结构模型具有尺寸大小完全相同的外形和内部钢骨架,两者主要的不同在于铺层和填充的材料。复合材料舵的最外层为0.01 m厚的玻璃钢,中间层为0.02 m厚的橡胶吸声材料,然后在最内部以钢骨架作为支撑,而在中间层与钢骨架之间的空腔中填充着浮体材料;钢质舵只包含厚度为0.03 m的外层钢质舵面以及内部的钢骨架。钢材的物理属性在2.2节中已经给出,复合材料的物理属性如表 1所示,其中橡胶吸声材料的杨氏模量与损耗因子以拟合公式[14-15]表示为
| $E = 1.102 \times {10^7} + 5\,\,447.2f - 3.515 \times {10^{ - 2}}{f^2}$ | (5) |
| $\eta = 0.401 + 1.21 \times {10^{ - 4}}f - 3.29 \times {10^{ - 9}}{f^2}$ | (6) |
|
|
表 1 复合材料物理参数 |
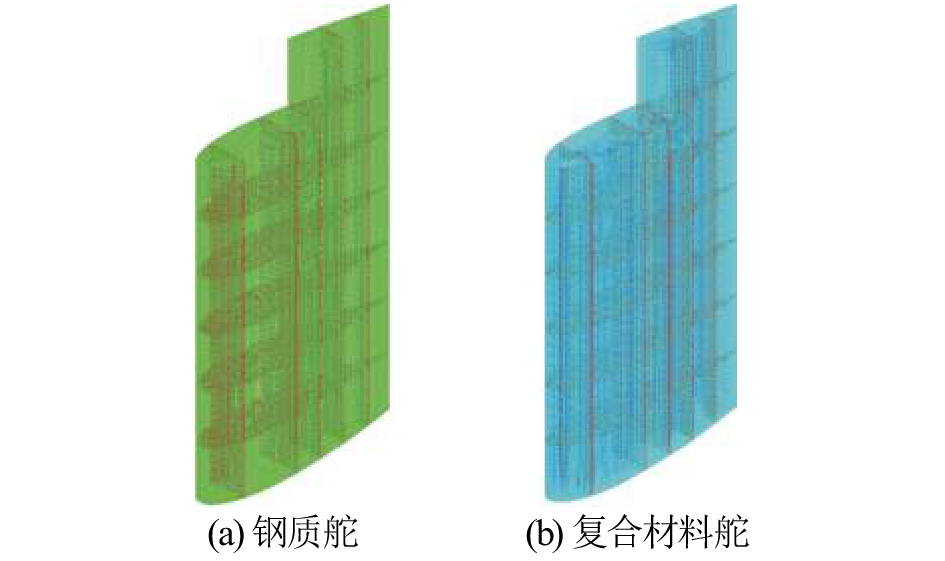
对于复合材料舵的有限元网格模型的建立,根据文献[16]中的研究可知,在进行结构振动特性分析时,以壳单元模拟表层玻璃钢、以实体单元模拟内部吸声材料和浮体材料的方法比起全部以实体单元模拟表层玻璃钢和内部材料的方法能够得到更为准确的计算结果,因此本文中的复合材料舵采用前一种方法进行有限元建模,而钢质舵则全部采用壳单元建立,网格尺寸统一为30 mm,网格模型如图 4所示。
|
Download:
|
| 图 4 舵结构有限元模型 | |
本文所述的正横方向,指的是舵结构的中纵剖面的垂直方向。正横目标强度作为研究对象最重要的声散射特性之一,在众多关于声散射目标强度的研究中经常置于首要的研究地位。因此,本文对舵结构的声散射的研究也从正横目标强度开始。
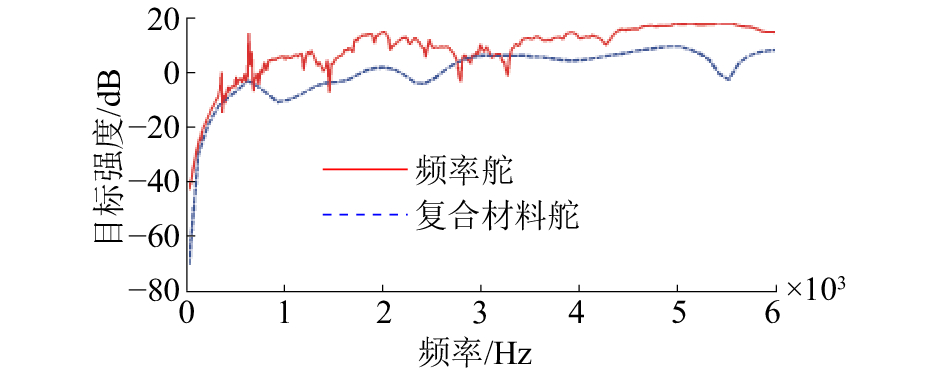
图 5给出了分别由钢材和复合材料构成的舵结构模型在平面波入射下的收发合置的正横声目标强度。曲线信息显示,在低于700 Hz的低频段内,复合材料舵的目标强度与钢质舵相比十分接近,而在800~1 400、1 500~2 700和3 400~6 000 Hz的中高频段内,复合材料舵的目标强度有着大约5~15 dB的降低,这与橡胶吸声材料的吸声特性有关。由式(6)得知,在本文的计算频段内,橡胶的损耗因子在低频较小,对声波的吸收不明显,但随着频率的增加,损耗因子不断的增大导致了目标强度的明显降低。另外,由于在低频段内,水中声波的波长要大于模型的特征尺寸,声波容易绕过模型向前方继续传播;而高频时,波长小于特征尺寸,声波的镜反射增加,绕射减少,目标强度不断上升,从而导致2种模型的计算结果从低频到高频上升的趋势。但是,随着频率的增加而导致的镜反射的增量将逐渐减小,使得目标强度不会无限制地增加,并且会与结构的二次辐射形成干涉从而出现波动。
|
Download:
|
| 图 5 随频率变化的正横目标强度曲线 | |
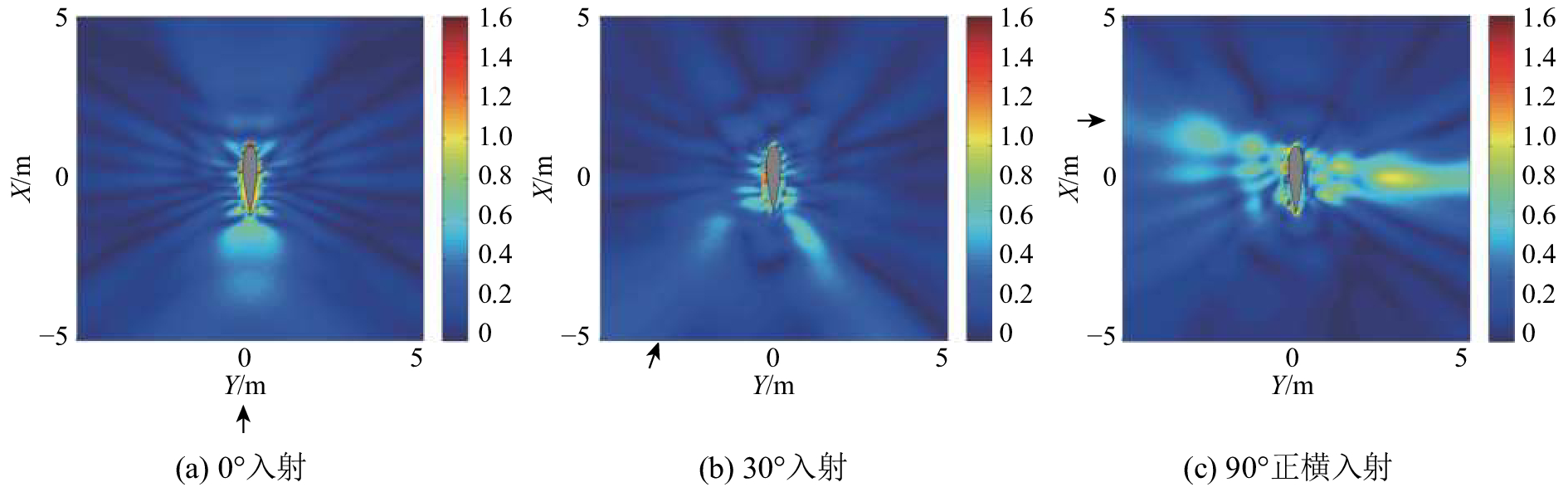
显然,正横目标强度只给出了从正横方向入射时结构在正横方向上的反向散射情况,而对于水平面内其他角度的响应则无法体现。因此,本小节对平面波单方向入射时水平面内周向其他角度在频率为4 000 Hz的响应进行计算,以声压云图的形式展示如图 6、7所示。在平面声波的照射下,对复合材料舵来说,声压较强的散射区域主要出现在舵的背面,而钢质舵的强散射则更多地出现在入射方向及其反方向上,并且钢质舵的反向散射声压在数值上更大一些,这表明钢质舵对声波的反射本领更强,而复合材料舵则更容易使声波透射或绕射过去。另一方面,由于声波在舵结构与流体介质的边界上形成强烈的干涉现象,从而在此边界附近形成了明显的散射亮点。对比不同入射角的情况发现,正横入射时舵的散射截面比小角度入射时大,相应的散射强度也更大,舵结构背面的强散射区也更大。而从图 6、7中看到的明显的镜反射现象分析,由于舵结构的曲面将入射波反射到其他方向,因此也可以解释在入射方向上的回波更小的现象。

|
Download:
|
| 图 6 复合材料舵在平面波入射下的XY平面(中横剖面)内的散射声压幅值 | |
|
Download:
|
| 图 7 钢质舵在平面波入射下的XY平面(中横剖面)内的散射声压幅值 | |
在3.3节中所述的散射声压云图描述了平面波照射下舵结构的散射声场的声压分布情况,而在本节中计算得到的如图 8所示的目标强度指向性则指明了结构在水平面内各个方向上的收发合置的目标强度的大小,所选的计算频率为100、1 000和4 000 Hz,分别对应着低频以及中高频段。从计算结果来看,随着频率的上升,舵结构的目标强度的数值变得更大,这与3.2节中的结论相一致。另一方面,舵结构声散射目标强度指向性的花瓣也逐渐增多,高频相比于低频出现了更强的指向性。另外,复合材料舵与钢质舵相比,其目标强度在大部分角度上都要更小,可见复合材料对于声散射目标强度的降低作用表现良好。再者,不同的入射角度也引起了目标强度的变化,90°和270°方向附近对应着最大的散射截面因而目标强度较大,0°和180°方向对应着最小的截面因而目标强度较小,从而使得如图 8所示的比较扁平的指向性图。

|
Download:
|
| 图 8 钢质舵(实线)和复合材料舵(虚线)结构在不同频率处的目标强度指向性 | |
通过有限元法对舵结构的散射声压及目标强度进行计算,可以得到以下结论:
1) 从正横目标强度看,复合材料在中高频段的吸声效果更好,并且目标强度的降低值大约在5~15 dB。
2) 散射声压云图则表现了不同材料的模型对平面声波的近场反射情况。对复合材料舵来说,声波容易透过或绕过结构而在舵的背面形成声压较强的散射区域,而钢质舵的强散射则更多地出现在入射方向及其反方向上。
3) 随频率的上升,舵结构指向性模式的花瓣逐渐增多,指向性变得更加明显。但是相比于钢质舵,复合材料模型的目标强度依然更低。另外,由于散射截面在正横方向最大,目标强度相应更大一些。
| [1] |
FLAX L, DRAGONETTE L R, ÜBERALL H. Theory of elastic resonance excitation by sound scattering[J]. The journal of acoustic society of America, 1978, 63(3): 723-731. DOI:10.1121/1.381780 ( 0) 0)
|
| [2] |
WILLIAMS K L, MARSTON P L. Synthesis of backscattering from an elastic sphere using the Sommerfeld-Watson transformation and giving a Fabry-Perot analysis of resonances[J]. The journal of the acoustical society of America, 1986, 79(6): 1702-1708. DOI:10.1121/1.393231 ( 0) 0)
|
| [3] |
MARSTON P L. Scattering of a Bessel beam by a sphere: Ⅱ. Helicoidal case and spherical shell example[J]. Journal of the acoustical society of America, 2008, 124(5): 2905-2910. DOI:10.1121/1.2973230 ( 0) 0)
|
| [4] |
李威, 李骏, 龚志雄. 水下任意刚性散射体对Bessel波的散射特性分析[J]. 物理学报, 2015, 64(15): 0154305. ( 0) 0)
|
| [5] |
GOEL G C, JAIN D L. Scattering of plane waves by a penetrable elliptic cylinder[J]. The journal of the acoustical society of America, 1981, 69(2): 371-379. DOI:10.1121/1.385463 ( 0) 0)
|
| [6] |
EVERSTINE G C. Finite element formulatons of structural acoustics problems[J]. Computers & structures, 1997, 65(3): 307-321. ( 0) 0)
|
| [7] |
李耀飞, 李威, 李骏, 等. 水下复合材料舵结构的声目标强度特性仿真[J]. 船海工程, 2015, 44(4): 21-24. DOI:10.3963/j.issn.1671-7953.2015.04.006 ( 0) 0)
|
| [8] |
SONG Feng, LI Wei, WANG Mingsheng. Study on acoustic target strength characteristics of underwater composite rudder[C]//Proceedings of the 30th International Conference on Vibroengineering. Phuket, Thailand, 2017: 87-90.
( 0) 0)
|
| [9] |
杨志刚, 王同庆. 边界元计算内外声场耦合及流体目标声散射[J]. 哈尔滨工程大学学报, 2007, 28(2): 161-164. DOI:10.3969/j.issn.1006-7043.2007.02.009 ( 0) 0)
|
| [10] |
张波. 浅海环境中水下物体声目标强度的物理意义[J]. 中国科学, 2013, 43(3): 239-248. ( 0) 0)
|
| [11] |
CHAI Yingbin, LI Wei, LI Tianyun, et al. Analysis of underwater acoustic scattering problems using stable node-based smoothed finite element method[J]. Engineering analysis with boundary elements, 2016, 72: 27-41. DOI:10.1016/j.enganabound.2016.08.005 ( 0) 0)
|
| [12] |
CHAI Yingbin, GONG Zhixiong, LI Wei, et al. Application of smoothed finite element method to two-dimensional exterior problems of acoustic radiation[J]. International journal of computational methods, 2018, 15(5): 1850029. DOI:10.1142/S0219876218500299 ( 0) 0)
|
| [13] |
詹福良, 徐俊伟. Virtual.Lab Acoustics声学仿真计算从入门到精通[M]. 西安: 西北工业大学出版社, 2013: 11-14.
( 0) 0)
|
| [14] |
张玉玲, 陶猛, 范军. 敷设吸声材料复杂目标的目标强度计算[J]. 上海交通大学学报, 2009, 43(8): 1322-1326, 1331. DOI:10.3321/j.issn:1006-2467.2009.08.028 ( 0) 0)
|
| [15] |
王仁乾, 马黎黎. 吸声材料物理参数优化的研究[J]. 声学技术, 2004, 23(2): 73-78. DOI:10.3969/j.issn.1000-3630.2004.02.001 ( 0) 0)
|
| [16] |
宋世伟, 吴梵. 复合材料稳定翼有限元分析方法对比研究[J]. 船舶工程, 2011, 33(5): 23-26. DOI:10.3969/j.issn.1000-6982.2011.05.006 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


