溃坝的发生往往会给社会及人民造成巨大的灾难，对于溃坝问题的研究一直在水利工程中有着重要的地位。而另一方面，溃坝流动是带自由液面的基本问题，此类问题因初始条件及边界条件简单，却能充分反映出翻卷、入水、破碎等复杂的自由液面现象而引起众多流体力学人士的关注。

Deborah M. Greaves^[1]基于VOF方法，以自适应网格对方柱水的坍塌及带障碍物坍塌过程进行了模拟，并进行了试验对比。Abdolmaleki等^[2]分别基于VOF方法和FLUENT软件对二维溃坝问题进行了计算。Jaswant等^[3]基于一种显式中心迎风格式进行了一维和二维的溃坝模拟计算以及带障碍物溃坝的计算。Brufau等^[4]基于Delaunay非结构网格对二维浅水方程进行求解，对二维溃坝问题进行了模拟分析。

本文通过求解N-S方程得出溃坝问题中流体的流态，通过VOF方法追踪自由液面位置，分析了溃坝问题中的液体流动、自由液面的演变和溃坝造成的冲击力，得到了与实验结果高度吻合的结果，证明了本文方法的精确性。

1 理论基础 1.1 控制方程

由流体的连续性方程可知，封闭计算域内流体的质量只能由通过边界的流体流动改变，其数学表达式可以写为

$\frac{{\partial \rho }}{{\partial t }} + \nabla \cdot (\rho {{V}}) = 0$

式中： $\rho $ 表示流体的密度， ${{V}} = (u,v,w)$ 代表速度。对于不可压缩流体，可以对连续方程做如下简化：

${\bf {\nabla}} \cdot {{V}} = 0$

流体的动量守恒方程也称作N-S方程，该定律的表述为，微元体中的动量对时间的变化率等于外界作用在该微元体上的各种力之和。这实际上是牛顿第二定律。

N-S方程有以下形式：

$\frac{{\partial \left( {\rho {{V}}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho {{V}} \otimes {{V}}} \right) = \nabla \cdot \left( {\mu \nabla \otimes {{V}}} \right) - \nabla P + {{g}} + {{{f}}_\sigma } + {{S}}$

(1)

式中： $\mu $ 为液–气的混合动力黏性系数， $P$ 为压力， ${{g}} = (0,0, - g)$ 为重力矢量， ${{{f}}_{{\sigma }}} = \sigma \kappa $ 为表面张力， ${{S}} = ({S_x},{S_y},{S_z})$ 为方程源项^[5]。式(1)左侧第2项称为对流项，右侧第1项称为扩散项。

1.2 控制方程离散及求解

采用有限体积法在交错网格之上离散控制方程，交错网格中，控制体的速度存储在网格边界上，其他标量存储在网格中心，这种变量存储方式有效避免了棋盘状压力分布。

对不可压连续方程在控制体上积分并应用高斯定理，得到连续方程的离散形式：

$\sum\limits_{nf = 1}^n {{{{u}}_f} \cdot {{{A}}_f} = 0} $

式中： ${{{u}}_f}$ 指界面处的速度向量， ${{{A}}_f}$ 指界面的面积矢量。

对于N-S方程，在控制体上积分之后，同样对对流项和扩散项使用高斯积分将体积分变换为面积分，而后分别对其采用一阶迎风格式和中心差分进行离散。

最终得到离散的N-S方程：

$\frac{{{{V}}_P^{t + \delta t} - {{V}}_P^t}}{{\delta t}}{V_P} + \sum\limits_{f = 1}^n {{\rho _f}{F_f}{{V}}_P^{t + \delta t}} = \sum\limits_{F = 1}^N {{\nu _f}{A_f} \cdot \left( {\nabla \otimes {{V}}} \right)_f^{t + \delta t} + {{{S}}_{{{{V}}_P}}}{V_P}} $

式中下标p和f分别代表交错网格的中心和边界。

N-S方程的求解是通过IDEAL^[6]算法实现的，其全称为内部双迭代高效算法。IDEAL算法基于semi-implicit method for pressure-linked equations (SIMPLE)开发而成。它通过对压力方程进行2次内部迭代计算，几乎完全舍弃了SIMPLE算法的2个基本假设，速度和压力得到了充分耦合，大大提高了算法的收敛性。

1.3 VOF和PLIC方法

VOF方法是基于流体体积分数 $F$ 这一概念提出的。流体体积分数为标量函数，定义为控制体积内特征流体所占体积与控制体体积的比值。以水为例，若控制体内没有水， $F$ 为0；若控制体被水充满， $F$ 为1；若有 $0 < F < 1$ ，则表示该控制体内有自由液面存在^[7]。

根据流体体积分数的定义，我们可以得出混合密度和混合动力黏性系数的表达式：

$\left\{\begin{aligned}& \rho = F{\rho _L} + (1 - F){\rho _G}\\& \mu = F{\mu _L} + (1 - F){\mu _G}\end{aligned}\right.$

流体体积分数的输运方程可以写为

$\frac{{\partial F}}{{\partial t}} + {{V}} \cdot \nabla F = 0$

由于VOF方法追踪的是网格中的流体体积，而不是追踪流体质点的运动，采用的施主–受主方法不仅要考虑本网格的流体体积分数，而且要用到相邻网格上的流体体积分数，以此来提高分辨率。因而具有容易实现、计算量小和精度高等优点，可以处理类似溃坝水流的自由面折叠的强间断问题^[8]。

在VOF方法中，在每个网格中定义流体体积分数 $F$ ，根据 $F$ 的值来重构自由液面的位置。PLIC方法将自由液面用网格内的一条斜线近似，这种方法较用垂直或水平线来近似自由液面的simple line interface calculation(SLIC)方法能更精确地表示出自由液面的形状，界面重构示例如图1所示^[5]。

由中心网格及其相邻的8个网格的流体体积分数，可确定自由液面的法向量^[9-10]，网格内用来近似自由液面位置的斜线就可以由此法向量和网格内的流体体积分数两者唯一确定。

1.4 表面张力的CSF模型

互不掺混的流体界面上一定存在表面张力，单位长度的表面张力称为表面张力系数，记为 $\sigma $ 。对于互不相溶流体来说 $\sigma > 0$ ；对于互溶的流体来说 $\sigma < 0$ 。

两相流体间的这种张力可用Young-Laplace方程来表示：

$\Delta P = {P_I} - {P_O} = \sigma \kappa $

式中： $\sigma $ 为表面张力系数， $\kappa $ 为液面曲率，P为压强，下标I、O分别代表曲面的凹形一侧和凸形侧。结构网格中曲率 $\kappa $ 可由自身及周围8个网格的流体体积分数确定^[11-12]。

2 数值模型

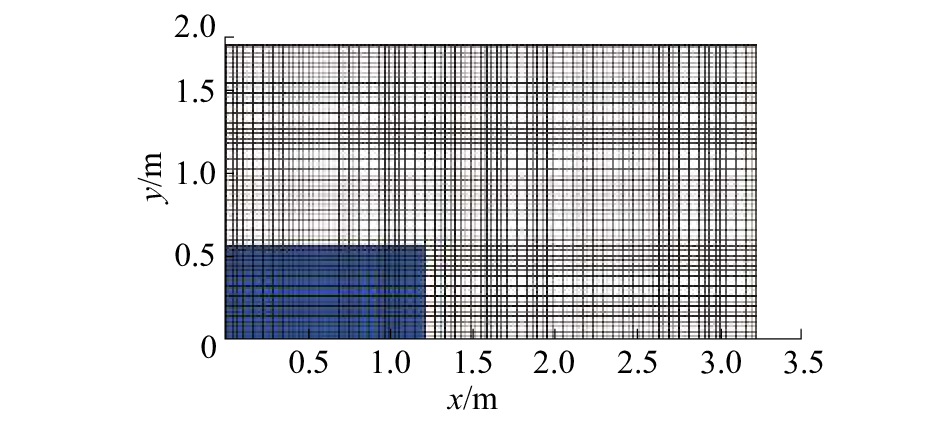
本文对二维溃坝的模拟采用文献[13]中的模型，示例见图2。图中，尺寸为0.6 m×1.2 m的水柱被一块挡板固定在长3.22 m，宽1.8 m的水箱左侧，在t=0时刻迅速抽去挡板，水柱开始向右坍塌。以此模型模拟溃坝水流的情形，观察过程中自由液面的演变。

基于正交结构网格进行计算中网格数量为161×90。箱体四周均为不可滑移壁面边界，压力初场由静压条件给出，并指定壁面上的初始压力为0。计算中，取水的密度 ${\rho _W} = 998.2\; {\rm{kg/}}{{\rm{m}}^{\rm{3}}}$ ，水的动力黏性系数 ${\mu _W} = 1.003 \times {10^{ - 3}}\; {\rm{N}} \cdot {\rm{S/}}{{\rm{m}}^{\rm{2}}}$ ；空气密度 ${\rho _A} = 1.225\; {\rm{kg/}}{{\rm{m}}^{\rm{3}}}$ ，空气的动力黏性系数 $ {\mu _A} ={\rm{1}}{\rm{.789}} {\rm{\,\,4}}\times $ $ {\rm{1}}{{\rm{0}}^{ - 5}} \;{\rm{N}} \cdot {\rm{S/}}{{\rm{m}}^{\rm{2}}}$ 。

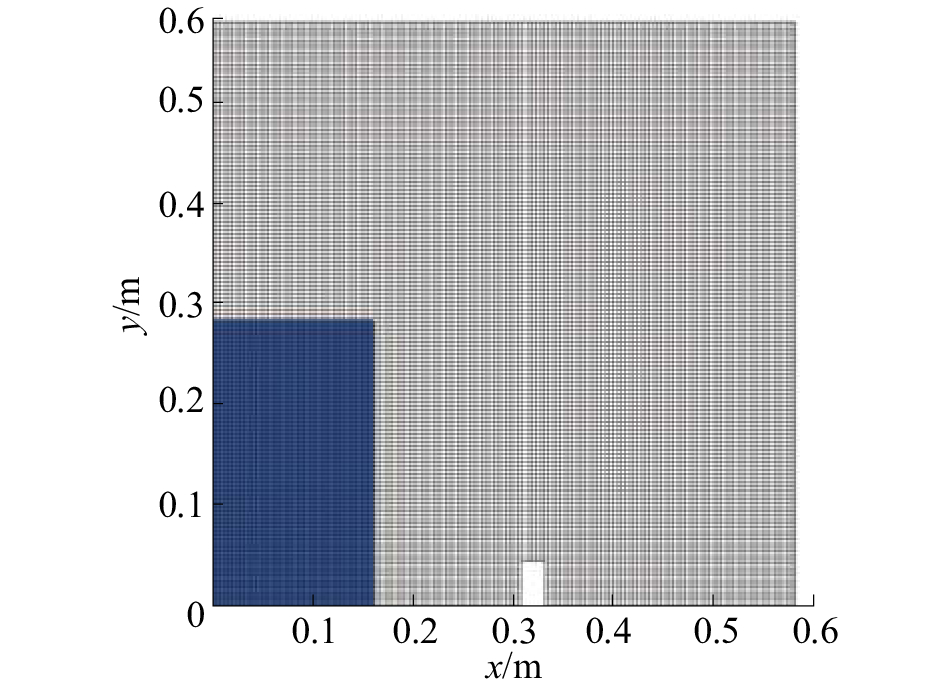
带障碍物的二维溃坝模拟采用文献[14]中的模型，示意图如图3所示。计算域为0.584 m×0.584 m的方舱，尺寸为0.294 m×0.1461 m的水柱被挡在方舱的左侧，在横坐标0.31 m右侧有高0.048 m、宽0.024 m的障碍物，在t=0时刻迅速抽去挡板，观察过程中自由液面的变化。在此部分数值模拟中用到的常数与上一部分一致。箱体四周均为不可滑移壁面边界，压力初场由静压条件给出，并指定壁面上的初始压力为0。障碍物表面设置为无滑移壁面，同时为保证障碍物的速度为0，应采用以下方法：1)在每一层次迭代前令障碍物内速度为0；2)令障碍物速度离散方程主元系数为一极大值，以保证速度预估值为0；3)令障碍物速度修正值计算式系数为一极小值，以保证速度修正值为0^[15]。

3 数值结果

本文模拟结果与文献[13]的模拟结果对比如图4(左侧一列为文献[13]的结果，右侧一列为模拟结果，下同)。

文献[13]的结果是基于光滑粒子流体动力学方法(SPH) 方法得到的。在t=1.19 s左右，液面由于重力开始翻卷下落；t=1.415 s时，本文的模拟结果更能突显出由于重力作用驱使的水头向下的趋势，而这一差别在t=1.824 s时得到了更明显的体现。

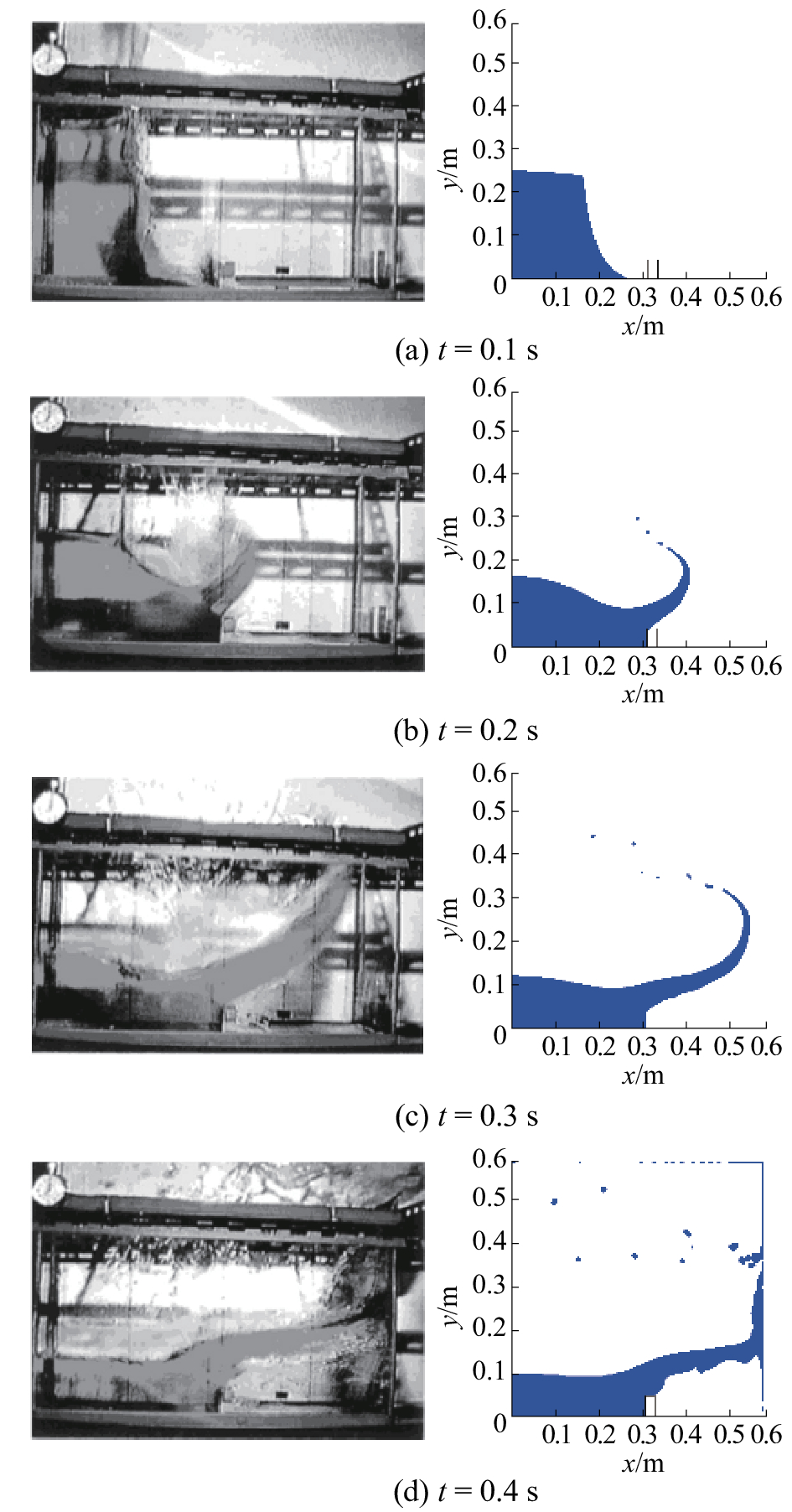
对于带障碍物的二维溃坝模拟，自由液面的演变及与文献[14]中的实验结果对比见图5。

对比试验结果和文中的计算结果，由于抽去挡板时对水柱造成了扰动，在0.1 s时实验结果水柱侧面有明显的不光滑，而在数值模拟中不会有这种现象。在0.2 s和0.3 s时，水舌的出现和甩出的水滴都得到了很好的模拟，然而数值模拟中并没有出现严重的液体飞溅。0.4 s时，由于数值模拟中水箱高度要大于试验，故模拟中水舌接触到侧壁后沿侧壁向上爬升而不是如实验中那样接触到顶壁然后翻卷，但基本的自由液面形状是一致的。

4 结论

本文以方形水柱的自由坍塌模拟了二维溃坝和带障碍物溃坝问题，可得到以下结论：1)文中对自由液面的数值模拟与实验结果有很高的一致性，证明了所采用方法的精确度；2)本文对溃坝水流的预估模拟可以为现实中防灾减灾措施提供参考；3)文中以二维近似三维，将程序拓展到三维进行更接近现实的模拟预测，或者尝试对可移动边界或障碍物进行处理都是以后可参考的研究方向。