2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
船舶艏部型线对于船舶阻力的影响很大,如果球鼻艏的大小、形状、位置与船体线型配合得合理,这对减小船体总阻力的作用是相当大的。船艏球鼻的形式较多,比较常用的有撞角形、水滴形、圆筒形和“S-V”形4种。杨大明等[1]在某肥大型船舶上应用前伸型球鼻艏,通过船模阻力试验与原型阻力试验结果对比,验证了在设计航速(11 kn)附近,改加了球鼻艏的新船型总阻力比原型船减少约12%;Zhang B J等[2]为了获得具有优异的阻力性能的船体形式,开发了具有自主知识产权的船体型线的优化设计方案,可以使得船舶阻力明显降低;Ma K等[3]基于线性波浪增阻理论和边界层分离控制技术,对船体设计水线以下的型线形状进行了优化研究;Hamasaki J等[4]船舶艏柱形式进行了改进研究,采用B样条曲线的系数作为设计变量,并通过Michill近似来估计波阻值,验证了该方法的可行性;兰林强等[5]对基于NURBS方法的船体完全参数化建模和基于Rankine源的面元法的船舶阻力数值计算进行了研究,验证了所提出型线优化设计方案的有效性。
本文主要是通过对2 000 t科考船采用某一船艏形式时的阻力性能进行试验及CFD数值计算进行研究,在此基础上优化设计出2种不同船艏形式,并对其阻力性能进行数值计算,对比研究了不同船舶艏部形式对其阻力性能的影响。
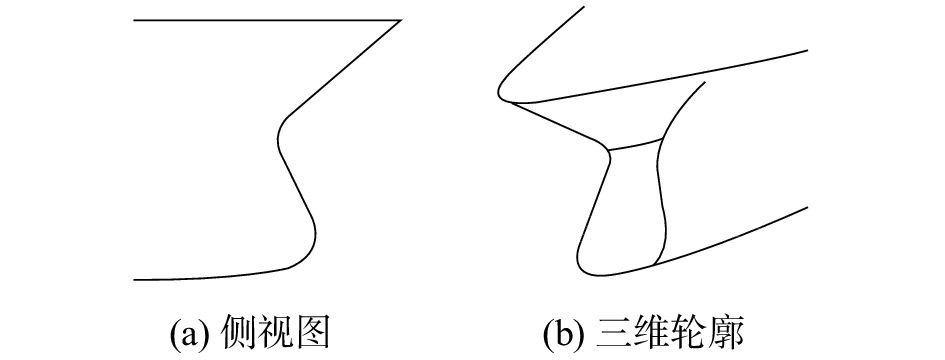
1 船舶总阻力数值计算及试验验证 1.1 基于CFD的船舶总阻力数值计算 1.1.1 船模参数及船艏形式2 000 t科考船船模主要尺度参数及其船艏型线轮廓如表1、图1所示。
|
|
表 1 船模主尺度参数 |
|
Download:
|
| 图 1 船艏形式轮廓(Hull B) | |
本文主要采用Star-CCM+软件对船模在一定航速区间内的阻力进行数值计算,为了更好地模拟船舶在航行过程的自由状态,在数值计算时设置六自由度运动控制函数保持船舶的纵倾及升沉;采用有限体积法(finite volume method,FVM)对控制方程进行离散求解,不可压缩黏性流体的控制方程[6-8]为
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0$ |
| $\begin{split}\frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + & \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = \\& - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right)} \right] + {f_i}\end{split}$ |
式中:
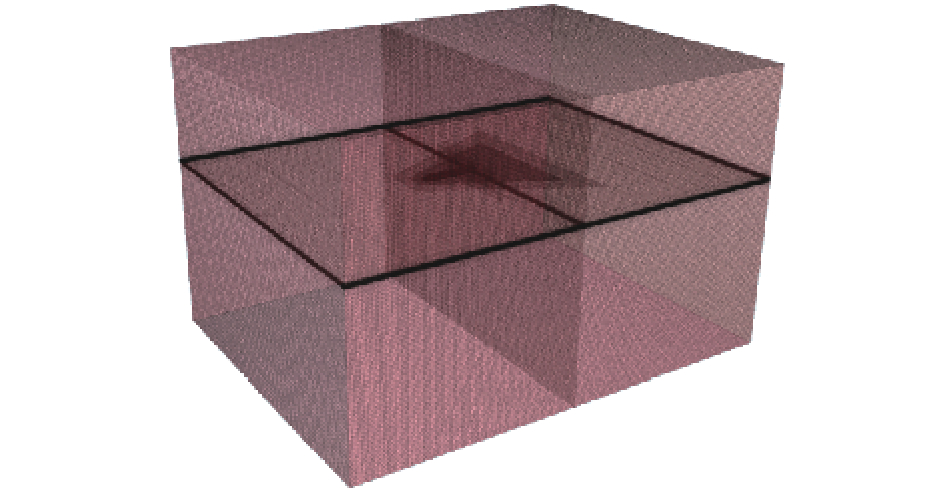
为了减少计算域边界对船体周围流场的扰动,将计算域设置为一个长方体用来模拟现实实验中的船模拖曳水池,计算域长方体设置长为7LOA,宽为6LOA,高为5LOA;边界设置除了出流口为压力出口外其余边界全部设置为速度入口,以此模拟无限大流域;对于船模CFD数值计算一般取经验值y+=150,△y=0.001;湍流度设置为0.001;湍流黏度比为10;由于船模在行进过程中会有兴波作用,兴波阻力对船模总阻力会有很大的影响,因此在水线面及船体表面周围进行网格加密处理,进行网格无关性验证之后计算域总的网格数量为263万;图2~4为计算域及自由液面网格加密设置。

|
Download:
|
| 图 2 计算域边界设置 | |
|
Download:
|
| 图 3 计算域Z向网格自由液面加密 | |

|
Download:
|
| 图 4 自由液面网格划分 | |
2 000 t科考船船模阻力试验是在哈尔滨工程大学船模拖曳水池中完成的(见图5),水池长108 m、宽7 m、深3.5 m、稳速0.1~6.5 m/s、精度0.1%。船模由拖车通过四自由度适航仪(精度0.1%)牵引,计算机数采系统(精度16 bit)实时记录各个航速下作用在船模上的力。船模艏部装有激流装置真实模拟湍流边界层。在阻力测量阶段,船模自由升沉、纵摇。阻力试验一般至少测量10~15个点,包含船模速度Vm(m/s)和该速度下的船模总阻力Rtm(N)[10-12]。

|
Download:
|
| 图 5 船模阻力实验设施 | |
通过船模阻力试验及数值计算,船模阻力随航速变化如图6。

|
Download:
|
| 图 6 船模阻力曲线 | |
由图6可知,在航速较低时数值计算与阻力试验值吻合度较好,随着航速的增加,二者的差距变大,阻力试验值大于数值计算,对比较高航速下数值计算和阻力试验值并计算其误差如表2所示。
|
|
表 2 数值计算和阻力试验误差 |
由表2可知,在高航速区间随着航速的增加,数值计算和船模试验阻力值二者的误差呈递增的趋势;但是在试验航速范围内最高误差值为2.90%,误差较小,验证了CFD数值计算在本次船模阻力对比研究中的可靠性,为对比不同船艏形式的船模阻力性能数值计算奠定了计算基础。
1.3.2 船模兴波及表面压力(Vm=2.061 m/s)由图7、8船模阻力试验录像及CFD数值计算展现的船体周围表面兴波状况可知,CFD数值计算在一定程度上真实反映了船体周围的流场变化,而且在试验航速范围内,较高航速下船艏兴波较大,水流在船模艏部区域沿着船体表面上升并产生翻卷,这与船体表面的压力分布变化也是相吻合的。

|
Download:
|
| 图 7 阻力试验及CFD计算船体兴波 | |

|
Download:
|
| 图 8 船艏兴波 | |
根据阻力试验所采用的船艏形式B进行优化改进设计,船艏外轮廓外延和内缩,同时保证型线的一致性和光顺性,船身其他部位型线保持不变。将船艏型线进行内缩记为A,外延记为C,其各自外部轮廓如图9所示。

|
Download:
|
| 图 9 不同船艏形式轮廓 | |
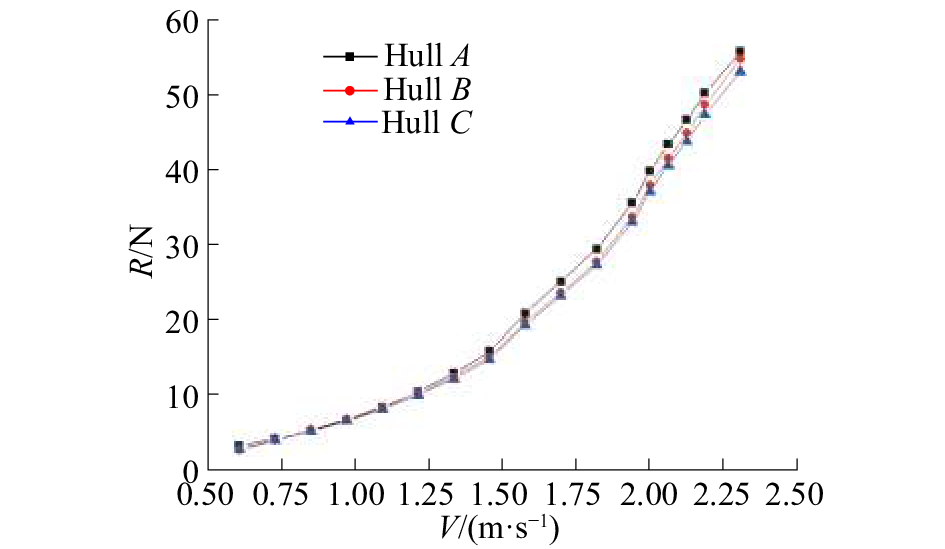
分别对3种不同船艏形式的船模总阻力进行数值计算,其阻力曲线变化如图10所示。
|
Download:
|
| 图 10 3种不同船艏形式船模阻力曲线 | |
由图10可知,船艏形式内缩使得船舶阻力增加,船艏形式外延使得船舶阻力降低;3种不同船艏形式船模阻力随航速变化趋势是一致的,在低速阶段三者阻力值差别不大,随航速的增加差别变得较为明显,如表3所示。
|
|
表 3 不同船艏形式船模总阻力变化 |
由表3可知,将船模艏部型线做适当外延设计可以有效地提高船模阻力性能;在所选取航速区间内B比A船模总阻力平均降低4.11%,C比A船模总阻力平均降低6.23%;而且随着航速的增加,船模阻力减额先上升然后再下降。
将船模总阻力分为摩擦阻力和压差阻力:
| ${R_{{t}}} = {R_{{f}}} + {R_{{p}}}$ |
式中:Rt为总阻力,Rf为摩擦阻力,Rp为压差阻力。
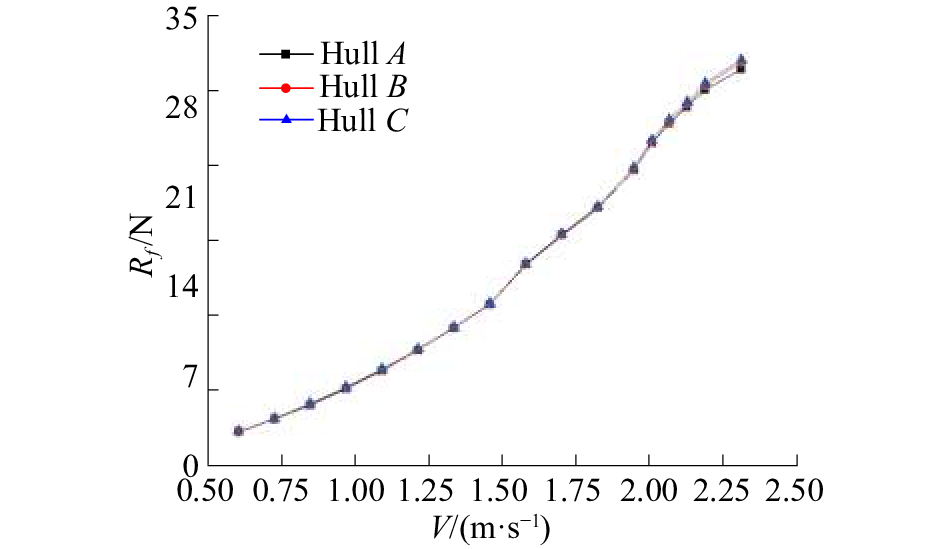
分别研究3种船艏形式下的摩擦阻力和压差阻力的变化,如图11、12所示。
|
Download:
|
| 图 11 3种不同船艏形式船模摩擦阻力曲线 | |

|
Download:
|
| 图 12 3种不同船艏形式船模压差阻力曲线 | |
由图11可知,不同船艏形式下的船模摩擦阻力曲线变化不大,由于船模艏部进行了不同程度的外延和内缩变化,船模的湿表面积也发生了相应的增加和减少,船模艏部外延所带来的摩擦阻力增额在0.57%左右。由图12可知,船艏型线变化对船模压差阻力的影响较大,船艏适当外延使得船模压差阻力减小,选取某一航速区间对比压差阻力变化见表4。
|
|
表 4 不同船艏形式船模压差阻力变化 |
由表4可知,不同船艏形式船模压差阻力变化对船模总阻力影响很大;在所选取航速区间内B比A船模压差阻力平均降低14.14%,C比A船模总阻力平均降低24.01%;而且随着航速的增加船模阻力减额先上升然后再下降,与船模总阻力的变化趋势相同。说明船模艏部外延主要是通过降低船模压差阻力来实现提高船模阻力性能的,但是随着航速的增加船模航行姿态发生变化产生抬艏现象,船艏对阻力影响减小;因此船模艏部型线的变化对阻力的改变会受到航速的影响。
3 结论本文主要对具有特定船艏形式的某2 000 t科考船的阻力性能进行了试验及数值计算,并以此优化设计出另外2种不同的船艏形式,分别对其阻力性能进行数值计算,通过本文的研究可以得出以下结论:
1)船舶球鼻艏的形式对船舶阻力性能有很大的影响,合适的船舶艏部型线对于船舶减阻性能提高产生积极地作用;
2)适当增加球鼻艏可以有效地提高船舶减阻性能,针对文中两种方案阻力平均降低5%左右;
3)阻力性能的改善会受到航速区间的影响,在本研究中阻力减额随着航速的增大呈现先增加后减小的趋势;
4)船舶球鼻艏外延程度的增加相对于整个船体总阻力的下降是否是一成不变的,如何借助试验的方法确定最优的船艏形式仍然需要继续深入的研究。
| [1] |
杨大明, 尹赟凯, 施奇. 某型低速船模型阻力试验研究[J]. 科学技术与工程, 2010, 10(13): 3296-3297, 3302. DOI:10.3969/j.issn.1671-1815.2010.13.066 ( 0) 0)
|
| [2] |
ZHANG Baoji. Research on optimization of hull lines for minimum resistance based on rankine source method[J]. Journal of marine science and technology, 2012, 20(1): 89-94. ( 0) 0)
|
| [3] |
MA Kun, TANAKA I. A study of optimal hull form for minimum resistance[J]. Journal of hydrodynamics, 1997, 12(1): 113-122. ( 0) 0)
|
| [4] |
HAMASAKI J I, HIMENO Y. Hull form optimization by nonlinear programming (Part 1): improvement of prismatic curve for minimizing wave resistance[J]. Journal of society of naval architects of Japan, 1995, 223: 29-34. ( 0) 0)
|
| [5] |
兰林强, 罗伟林. 基于参数化建模和CFD数值模拟的船舶球鼻艏优化设计[J]. 机电工程, 2016, 33(11): 1329-1333, 1353. ( 0) 0)
|
| [6] |
易文彬, 王永生, 杨琼方, 等. 实船阻力及流场数值预报方法[J]. 哈尔滨工程大学学报, 2014, 35(5): 532-536. ( 0) 0)
|
| [7] |
MENTER F R. Zonal two equation k-ω models for aerodynamic flows[R]. AIAA Paper. Orlando, USA: AIAA, 1993.
( 0) 0)
|
| [8] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 ( 0) 0)
|
| [9] |
赵松年, 于允贤. 湍流问题十讲: 理解和研究湍流的基础[M]. 北京: 科学出版社, 2016.
( 0) 0)
|
| [10] |
俞湘三. 船舶性能实验技术[M]. 上海: 上海交通大学出版社, 1991.
( 0) 0)
|
| [11] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004.
( 0) 0)
|
| [12] |
姜次平, 邵世明. 船舶阻力[M]. 上海: 上海交通大学出版社, 1985.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


