天然气作为一种清洁能源,其全球贸易量与日俱增。为了便于储存运输,常将天然气净化处理后常压冷却至-162 ℃,转变为液态天然气(liquid natural gas, LNG)。之后,LNG接收站将LNG加压到外输压力,送至气化器进行气化。气化过程中,管内的高压天然气在升温时发生了跨临界转变,其传热过程属于超临界流体传热过程。
超临界流体(supercritical fluid, SCF)是指温度、压力均高于临界值(Tc, Pc)时物质的一种状态,但目前也将压缩流体(即P>Pc, T < Tc)归于超临界流体范围。SCF具有很多独特的性质,如有很强的溶解低挥发性物质的能力、表面张力为零、扩散系数大等。同时,SCF的密度与液体接近,黏度却近似气体,使其在相同流量下的流动湍流程度更大,有利于传热的进行。而且,SCF由于其物理化学性质随温度压力连续变化,无相变潜热,是一种良好的传热介质,被广泛用于火力发电厂和核反应堆的冷却系统。但是,由于SCF相关物性在临界点附近的狭窄区间变化十分剧烈,使其流动传热过程十分复杂,引起了诸多学者的广泛关注。
Schmidt等通过研究发现近拟临界点附近SCF的自然对流强度非常大。Pioro等[1]则将超临界水用于蒸汽发生器,以提高火电厂的效率。Yu等[2]通过实验,研究了管内超临界水传热过程中浮升力效应的影响,并分析了质量流量、热流密度、压力等操作条件的影响。Gu等[3]对超临界深冷甲烷在毛细管内的流动传热进行实验研究,同样探讨了质量流量、热流密度、压力等操作条件对传热的影响。粘权鑫[4]通过对换热管进行等距分段的方法,得到了沿程传热系数的变化。韩冬艳[5]通过理论计算,采用温度分段的方法比较了现有描述管内传热的三类9种模型,认为Petukhov模型更适用于超临界天然气在管内的流动传热。靳书武[6]利用标准k-ε模型和定壁温条件,对水平圆管内的超临界甲烷流动传热进行研究,得到了压力、水浴温度等对管内表面传热系数影响。张康、董文平等[7-8]利用RNG k-ε模型和定热流密度条件,分析了超临界天然气的传热特性。
本文以浸没燃烧式气化器蛇形盘管内超临界天然气的流动传热为背景,利用Fluent 18.0进行数值模拟分析,分析超临界天然气在定外壁温换热管内的流动传热特性,研究不同操作条件对流动传热的影响,并与现有超临界流体管内传热的关联式进行比较。
1 模型的建立及求解 1.1 问题描述与物性计算以某在役浸没燃烧式气化器为模型,对其管内超临界天然气的流动传热进行模拟研究。其相关操作参数如表 1所示。
|
|
表 1 浸没燃烧式气化器操作参数 |
为了对超临界天然气在蛇形盘管内的流动传热进行模拟研究,做出以下假设:
1) 由于LNG内甲烷含量占85%以上,为简化模型,管内流体按甲烷单质处理;
2) 在浸没燃烧式气化器工作的过程中,其壳程水浴环境由于受燃烧烟气的扰动而使各个位置的温度分布均匀,因此设定其蛇形盘管的外壁温度恒定;
3) 流体在管内流动时沿程压降远小于操作压力,故管内按恒定压力处理;
4) 模拟的流动过程已达到稳定工况。
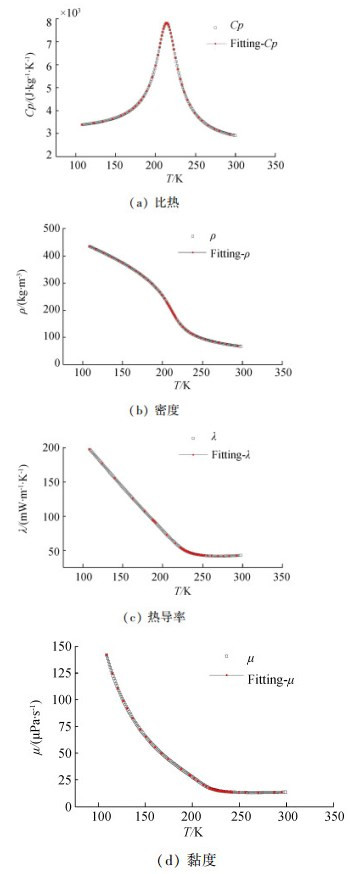
由于超临界甲烷在升温过程中物性变化剧烈,故采用美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)开发的软件REFPROP查询8.88 MPa下甲烷的相关物性,再利用Fluent自带的线性插值功能定义物性,插值结果如图 1所示。
|
Download:
|
| 图 1 8.88 MPa下甲烷的物性与插值结果 | |
图 2所示为该浸没燃烧式气化器的换热管结构尺寸,其中换热管外径D为25.4 mm,壁厚2 mm,两端长直管段长L1为7 600 mm,中间短直管段长L2为7 200 mm,大弯管半径R1为114 mm,小弯管半径R2为56 mm。

|
Download:
|
| 图 2 模型尺寸 | |
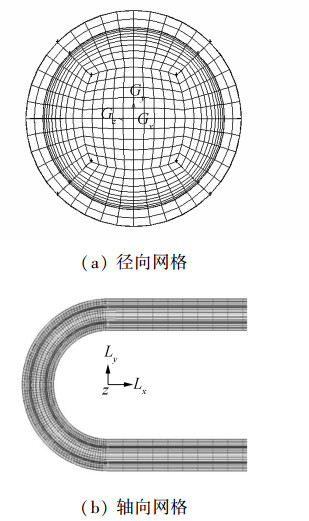
边界条件的设置上,选用质量入口、压力出口为换热管的进出口条件,设定进口质量流量和温度,出口压力等;换热管外壁选用定壁温条件,设定为水浴温度;内壁设为耦合壁面。本文利用Gambit 2.4.6对计算模型进行网格划分,网格全部采用结构化网格,同时为了更好地模拟弯头处复杂的流动情况,对该位置进行局部加密处理。网格结构如图 3。
|
Download:
|
| 图 3 网格划分示意 | |
由于计算时采用了标准壁面函数,故与壁面相邻的第1层网格节点应位于湍流的充分发展区,在黏性底层内不布置任何节点。在划分网格时,根据量纲为1的数y+对第1层网格高度进行估算,y+定义如式(1)所示,保证计算完后y+值在30~300之间,且接近30。
| $ {y^ + } = \frac{{y{U_\tau }}}{\mathit{\boldsymbol{v}}} $ | (1) |
式中:Uτ为壁面摩擦速度,m·s-1;
计算过程中,流体的流动传热满足稳态情况下的控制方程,如式(2)~(6)。
连续性方程:
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0 $ | (2) |
式中:xi为i方向;ρ为流体的密度,kg·m-3;ui为流体速度在方向上的分量,m·s-1。
动量方程:
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_i}}} + \rho {g_i} $ | (3) |
式中:p为流体静压力,Pa;τij为流体受到的切应力,Pa;gi为重力加速度在i方向上的分量,m·s-2。
能量方程:
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}T} \right) = \frac{\partial }{{\partial {x_i}}}\left( {\frac{\lambda }{{{c_p}}}\frac{{\partial T}}{{\partial {x_i}}}} \right) $ | (4) |
式中:T为流体温度,K;λ为流体的热导率,W·m-1·K-1;cp为流体的定压比热容,J·kg-1·K-1。
湍动能k的控制方程:
| $ \begin{array}{l} \rho {u_j}\frac{{\partial k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;{\mu _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \varepsilon \end{array} $ | (5) |
式中:k为流体的湍动能,m2·s-2;μ为流体的动力黏度,Pa·s;μt为流体湍流黏度,Pa·s,μt=cμρk2/ε,cμ为系数;σk是湍动能的普朗特数;ε是湍流耗散率。
湍流耗散率ε的控制方程:
| $ \begin{array}{l} \rho {u_k}\frac{{\partial \varepsilon }}{{\partial {x_k}}} = \frac{\partial }{{\partial {x_k}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_k}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{c_1}\varepsilon }}{k}{\mu _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - {c_2}\rho \frac{{{\varepsilon ^2}}}{k} \end{array} $ | (6) |
式中:c1、c2为系数;σε为湍流耗散率的普朗特数。不同k-ε模型的区别主要体现在k和ε方程中的系数cμ、c1、c2、σk、σε的不同。本文使用对二次流模拟较好的RNG k-ε模型,其系数为理论分析得出而非实验数据,其取值可见文献[9],在此不再赘述。
本文采用SIMPLEC算法。在对对流项的离散上,湍流脉动能方程和湍流耗散率方程采用二阶迎风格式离散;动量方程和能量方程采用QUICK格式离散。计算时对出口温度和质量流量进行监控,当相关出口参数稳定且残差达到收敛标准后,即认为计算收敛。
管程内壁表面传热系数按照式(7)进行计算:
| $ {h_i} = \frac{q}{{{T_w} - {T_b}}} $ | (7) |
式中:hi为内壁表面传热系数,W·m-2·K-1;q为局部壁面热通量,W·m-2;Tw为截面管壁平均温度,K;Tb为截面流体平均温度,K。
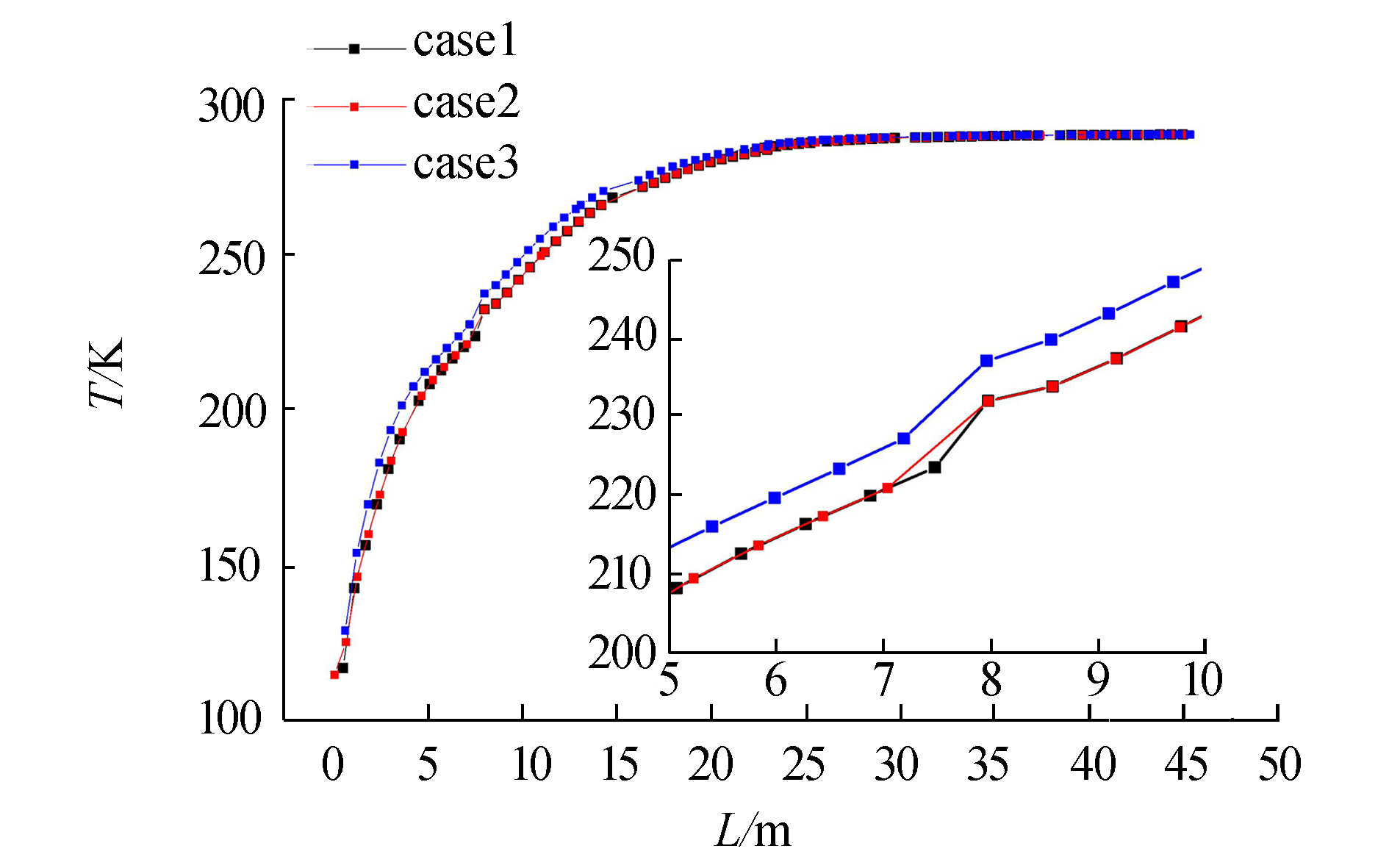
1.4 模型验证为了验证计算结果与网格的无关性,改变轴向和径向网格尺寸,如表 2所示,对计算结果进行对比,从图 4可以发现case2与case1计算结果基本一致,而case3偏差较大。考虑到计算的准确性和计算效率,本文选用case2进行计算。
|
|
表 2 网格无关性验证 |
|
Download:
|
| 图 4 不同Case计算结果比较 | |
根据在役SCV运行结果,对模型进行验证。模型模拟出口温度为15 ℃,满足其外输天然气的温度要求,证明了本模型采用的数值方法的准确性,可利用其进行进一步研究。
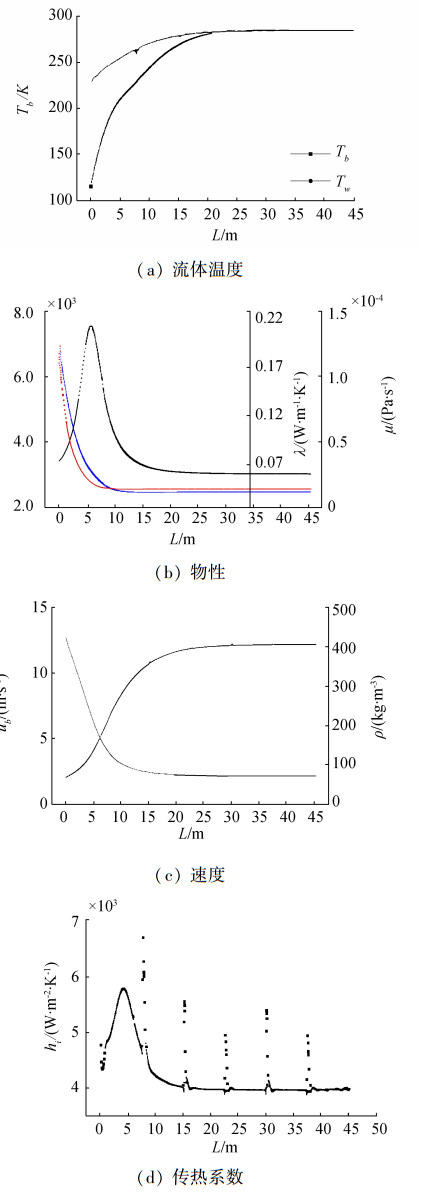
2 结果与讨论 2.1 流动与传热分析图 5所示为流体流动过程中,流体主流温度和内壁温度、相关物性、主流平均速度和管内截面平均传热系数随换热管长的变化规律。可以看出,随流动换热的进行,壁温和主流温度逐渐趋于水浴温度,且温差逐渐变小。在弯头处由于传热强化,使局部内壁温度偏低,但波动幅度逐渐减小。另外,流体主流温度的变化在拟临界点位置附近较平缓,偏离该区域后再次大幅上升。而从速度分布可以看出,由于流体密度随温度升高而降低,故管内流速不断增大。
|
Download:
|
| 图 5 管内流体温度、物性、速度和传热系数沿管长的变化规律 | |
从图 5中可以看出,在入口段,管内传热系数先下降后增大,这与入口段流体流动还未充分发展有关,由于入口段热边界层较薄,局部表面传热系数较充分发展段偏高,随流体逐渐发展充分,在湍流扰动作用下表面传热系数沿主流方向先下降后增大。在充分发展区,管内传热系数随换热管长先增大后减小,在拟临界点位置出现峰值,这与该位置定压比热容较大有关。另外,在弯管位置可以看出,由于流动方向改变造成二次流,使传热得到显著强化,并且弯头曲率半径越小,传热强化效果越明显。
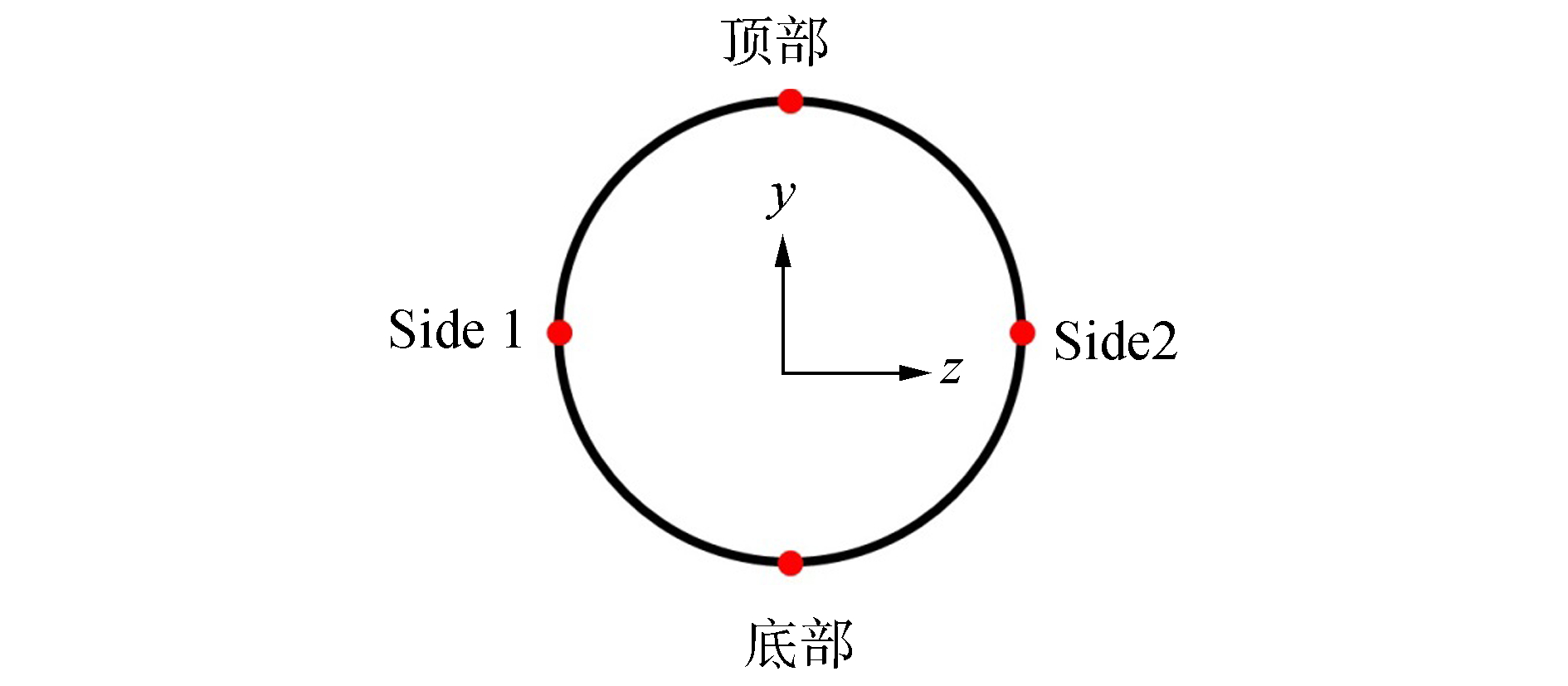
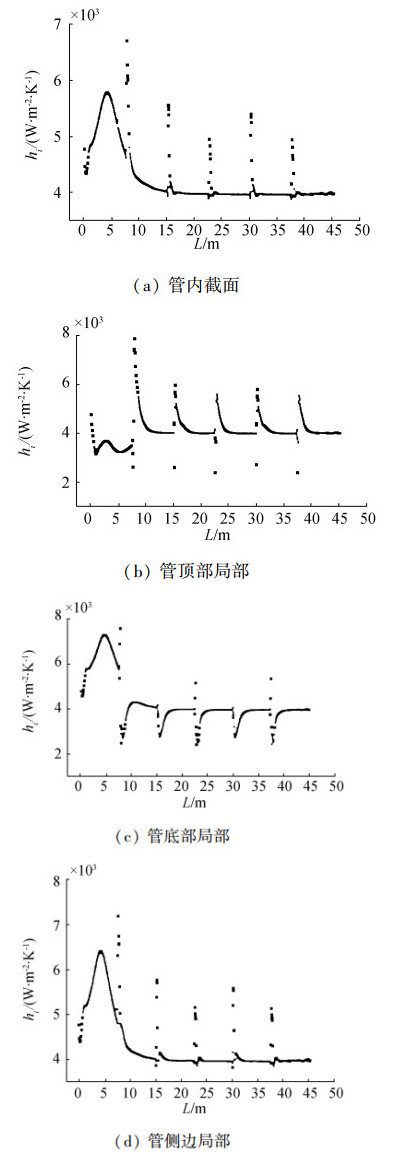
选取如图 6所示的换热管环向4个位置,分析换热管环向局部传热系数沿管长的变化规律,结果如图 7所示。可以看出相比于截面平均传热系数,在第一排管束,即剧烈升温部分的换热管顶部的传热系数偏低约32%,但弯头处局部强化效果更明显;管底部在剧烈升温段系数偏大约22%,但在弯头处却发生了传热的恶化;管侧边局部传热系数与截面平均传热系数较为接近。由于流体在水平段流动时,在浮升力与重力作用下密度较小的热流体积聚在管的顶部,密度较大的冷流体积聚在管的底部,而流体热导率随温度的升高而降低,造成顶部传热热阻较大,底部热阻较小,从而使传热系数出现差异。而在弯头处,由于流动方向改变,原来在管顶部的热流体在经过弯头后未重新回到管顶部时积聚在新管段的底部,因此分别造成了顶部底部的传热强化与恶化。
|
Download:
|
| 图 6 换热管环向4个位置分布 | |
|
Download:
|
| 图 7 换热管环向局部传热系数沿管长的变化 | |
1) 质量流量
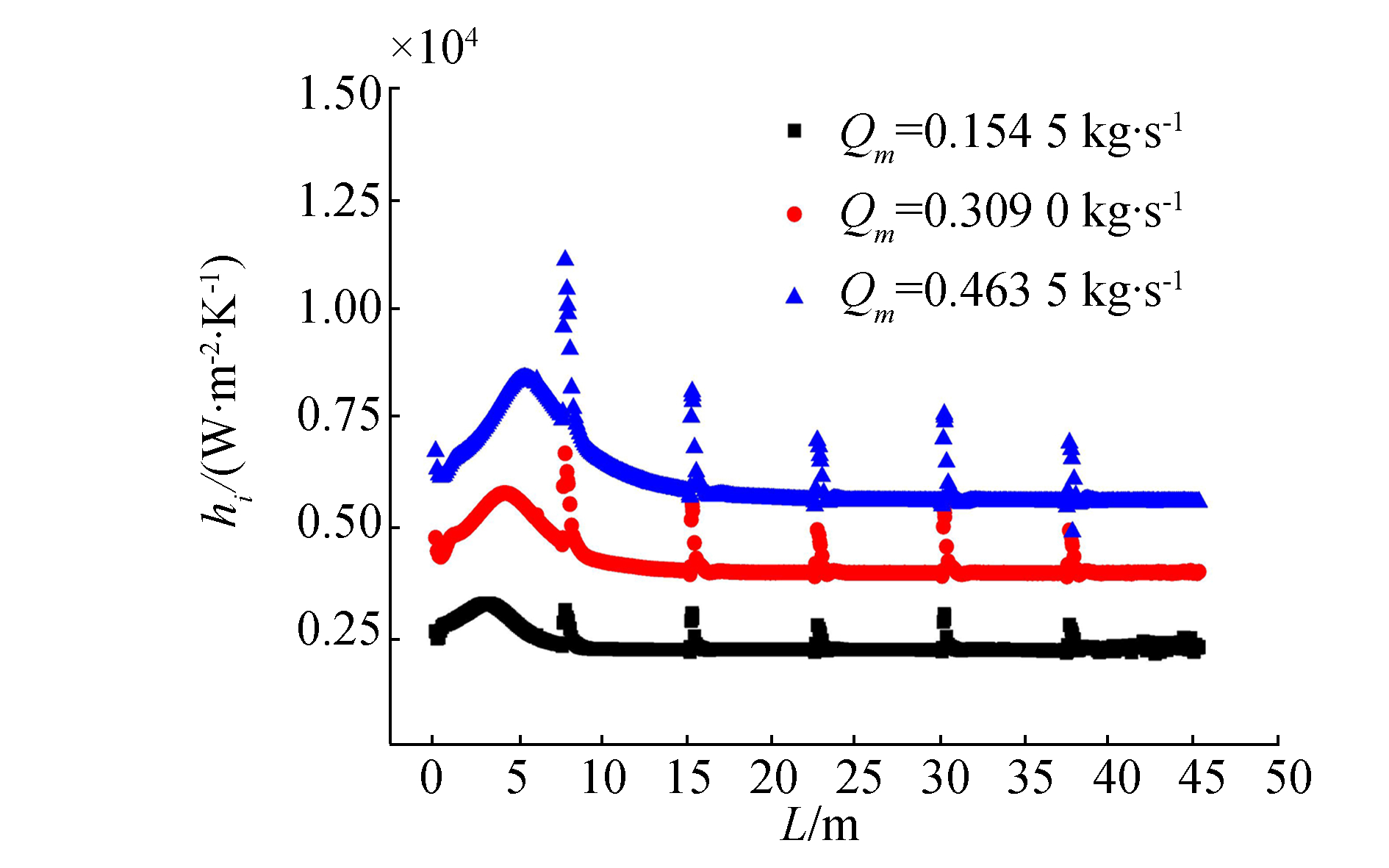
图 8为质量流量对传热系数的影响。从图 8中可以看出,质量流量越大,传热系数越高,且流体跨临界位置相对延后。当管内流速增大时,流体的湍流程度增加,有利于削薄边界层,对传热起到强化作用。但是流速增大使流体流过同一控制体时的时间减小,虽然传热系数增大,但传热不充分,故升温较慢,跨临界位置延后。
|
Download:
|
| 图 8 质量流量对传热系数的影响 | |
2) 入口温度
如图 9所示为入口温度对传热系数的影响。从图 9中可以看出,入口温度增加,传热系数变化不大,但流体跨临界位置稍稍提前,且第1个弯头处传热系数偏小。这是由于入口温度增加使流体能更快地达到拟临界温度,且第1个弯头处温度偏高(拟临界温度之上),比热容偏小,传热系数偏小。

|
Download:
|
| 图 9 入口温度对传热系数的影响 | |
3) 水浴温度
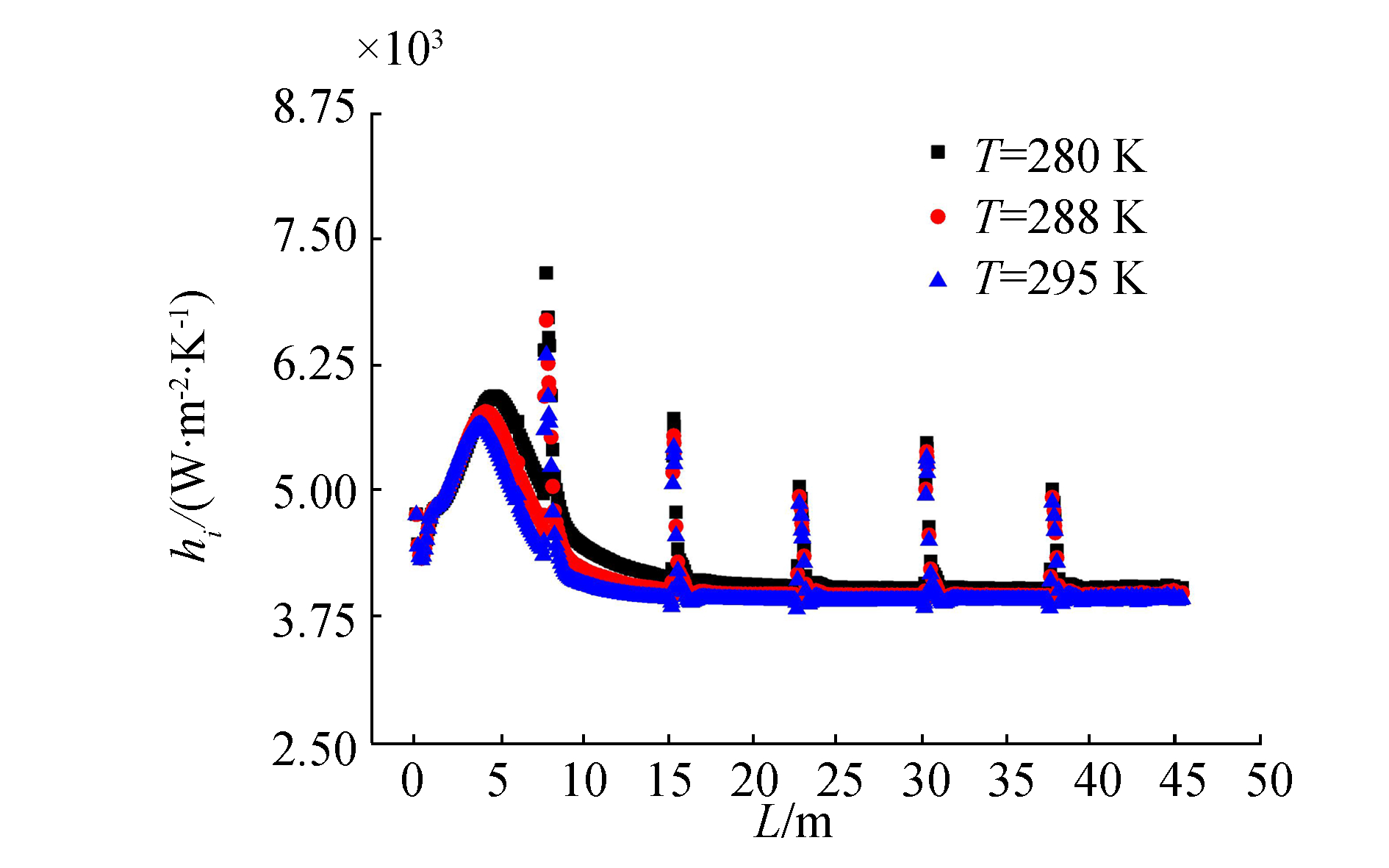
如图 10所示为水浴温度对管内传热系数的影响。可以看出,水浴温度增大同样会使流体跨临界位置提前,且影响效果强于入口温度。另外,传热系数峰值随水浴温度升高而降低,这是由于水浴温度越高,相同位置处的热导率越低,增大了导热热阻,使传热系数下降。
|
Download:
|
| 图 10 水浴温度对传热系数的影响 | |
目前,关于超临界流体在管内流动的传热特性已有诸多关联式对其进行描述,但尚不能统一。本文挑选其中较为经典的4个关联式,与模拟结果进行对比。
Dittus与Boelter等[10]提出的管内单相流体强制对流传热的关联式是目前工程上应用最为广泛的,其公式形式为
| $ N{u_b} = 0.023\mathit{R}{\mathit{e}_b}^{0.8}\mathit{P}{\mathit{r}_b}^n $ | (8) |
式中:Nu是流体对流传热的平均努塞尔数,Nu=hid/λ;Re为流体的雷诺数,Re=ρud/μ;Pr为流体的普朗特数,Pr=μcp/λ;下标b指管横截面流体的平均参数;上标n,当流体被加热时取0.4,流体被冷却时取0.3。
对于超临界流体在管内的混合对流传热,Jackson和Hall等[11]提出了新的经验关联式:
| $ N{u_b} = 0.018\;3\mathit{R}{\mathit{e}_b}^{0.82}\mathit{P}{\mathit{r}_b}^{0.5}{\left( {\frac{{{{\bar c}_p}}}{{{c_{pb}}}}} \right)^n}{\left( {\frac{{{\rho _w}}}{{{\rho _b}}}} \right)^{0.3}} $ | (9) |
式中:下标w指壁面温度下的相关物性;cp指截面流体平均比热,J·(kg-1·K-1);
当Tb < Tw < Tpc、1.2Tpc < Tb < Tw时,n=0.4;当Tb < Tpc < Tw时,n=0.4+0.2(
式中Tpc指流体在对应压力下的的拟临界温度,K。
Jackson和Fewster[12]也提出了对应的关联式:
| $ N{u_b} = 0.018\;3\mathit{R}{\mathit{e}_b}^{0.82}\mathit{P}{\mathit{r}_b}^{0.5}{\left( {\frac{{{\rho _w}}}{{{\rho _b}}}} \right)^{0.3}} $ | (10) |
Petukhov关联式[13]:
| $ N{u_b} = \frac{{\left( {f/8} \right)\mathit{R}{\mathit{e}_b}\mathit{P}{\mathit{r}_b}}}{{1 + \left( {900/\mathit{Re}} \right) + 12.7{{\left( {f/8} \right)}^{0.5}}\left( {\mathit{\bar P}{\mathit{r}^{2/3}} - 1} \right)}} $ | (11) |
式中:f指加热状态下的摩擦阻力系数,
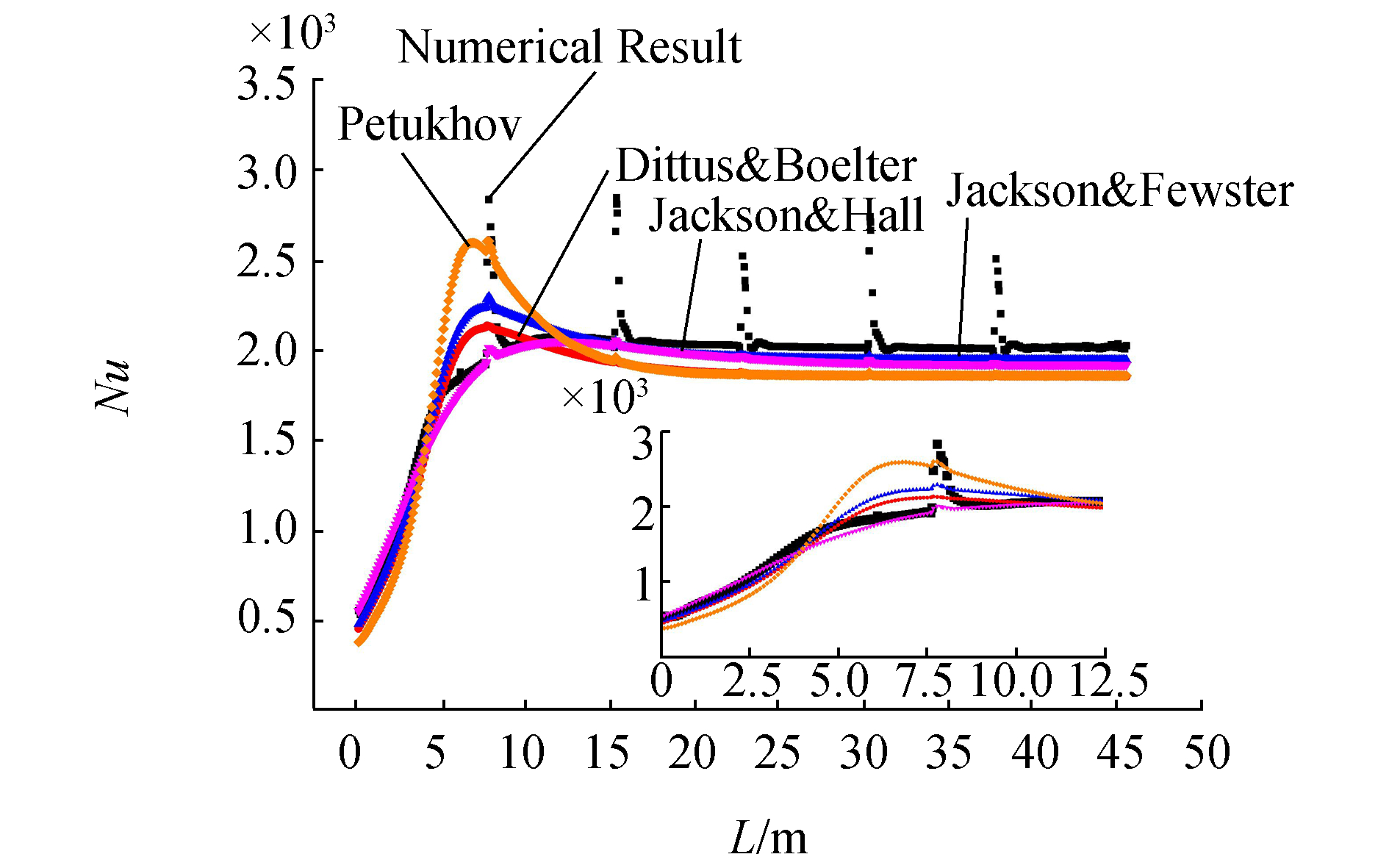
图 11为模拟结果与式(9)~(11)4个传热关联式计算结果的对比。从图 11中可以看出,Jackson & Hall关联式与模拟结果基本吻合,平均相对误差约为4.84%,但在流体跨临界之后,该关联式的计算结果偏低约5%;而Dittus & Boelter公式、Jackson & Fewster公式与Petukhov公式与模拟结果偏差较大,平均相对误差分别为8.17%、5.03%和10.85%,且均在近临界区域的计算结果偏高,超临界区域结果偏低。另外,从图中还可以看出4个公式对超临界流体在弯头处由于二次流引起的传热强化作用不能体现或体现不够,偏差可达30%以上,但考虑到弯头部分换热管长占总管长的比例较小,对总平均传热系数影响较小,故可以对其进行简化处理。
|
Download:
|
| 图 11 模拟结果与已有传热关联式的对比 | |
本文通过建立超临界天然气在浸没燃烧式气化器蛇形盘管中流动的相关模型,对管内超临界流体流动传热过程进行了相关研究,得到以下结论:
1) 换热管内壁温和流体主流温度逐渐趋于水浴温度,但在弯头处,由于传热强化使局部内壁温度偏低,波动幅度随换热进行逐渐变小;由于流体密度随温度升高而降低,使管内流速不断增大;入口段未充分发展的流体流动使传热系数先下降后增大,而在充分发展区,管内传热系数随换热管长先增大后减小,在拟临界点位置出现峰值。另外,在弯管处二次流的影响下,使传热得到显著强化,并且弯头曲率半径越小,传热强化效果越明显。
2) 比较换热管环向局部传热系数沿管长的变化发现,管顶部的局部传热系数偏低,但弯头处局部强化效果更明显;管底部局部传热系数偏大,但在弯头处却发生了传热的恶化;管侧边局部传热系数与截面平均传热系数较为接近。
3) 提高管内质量流量能够显著强化管内传热,但流体跨临界位置相对延后;提高管程入口温度和水浴温度均使流体跨临界位置提前,且较高的水浴温度会使传热系数峰值偏低。
4) 通过比较已有关联式与模拟结果发现,Jackson & Hall关联式与模拟结果基本吻合,平均相对误差约为4.84%,最为吻合;而Dittus & Boelter公式、Jackson & Fewster公式与Petukhov公式与模拟结果偏差均较大;各个关联式对超临界流体在弯头处的传热强化预测不够准确,偏差最大可达30%以上。
| [1] |
PIORO I L, DUFFEY R B, DUMOUCHEL T J. Hydraulic resistance of fluids flowing in channels at supercritical pressures (survey)[J]. Nuclear engineering and design, 2004, 231(2): 187-197. ( 0) 0)
|
| [2] |
YU Shuiqing, LI Huixiong, LEI Xianliang, et al. Influence of buoyancy on heat transfer to water flowing in horizontal tubes under supercritical pressure[J]. Applied thermal engineering, 2013, 59(1/2): 380-388. ( 0) 0)
|
| [3] |
GU Hongfang, LI Hongzhi, WANG Haijun, et al. Experimental investigation on convective heat transfer from a horizontal miniature tube to methane at supercritical pressures[J]. Applied thermal engineering, 2013, 58(1/2): 490-498. ( 0) 0)
|
| [4] |
粘权鑫, 郭少龙, 方文振, 等. 液化天然气浸没燃烧式气化器数值模拟方法研究[J]. 西安交通大学学报, 2016, 50(1): 67-71, 114. ( 0) 0)
|
| [5] |
HAN Dongyan, XU Qinqin, ZHOU Dan, et al. Design of heat transfer in submerged combustion vaporizer[J]. Journal of natural gas science and engineering, 2016, 31: 76-85. DOI:10.1016/j.jngse.2016.03.017 ( 0) 0)
|
| [6] |
靳书武, 武锦涛, 银建中. 水平圆管内超临界甲烷对流换热数值模拟[J]. 应用科技, 2015, 42(5): 67-71. ( 0) 0)
|
| [7] |
张康, 韩昌亮, 任婧杰, 等. SCV蛇形换热管内超临界LNG传热特性数值模拟[J]. 化工学报, 2015, 66(12): 4788-4795. ( 0) 0)
|
| [8] |
董文平, 任婧杰, 韩昌亮, 等. 浸没燃烧式气化器换热管内跨临界液化天然气的传热特性[J]. 化工进展, 2017, 36(12): 4378-4384. ( 0) 0)
|
| [9] |
陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001.
( 0) 0)
|
| [10] |
DITTUS F W, BOELTER L M K. Heat transfer in automobile radiators of the tubular type[J]. International communications in heat and mass transfer, 1985, 12(1): 3-22. ( 0) 0)
|
| [11] |
JACKSON J D. Consideration of the heat transfer properties of supercritical pressure water in connection with the cooling of advanced nuclear reactors[C]//Proceedings of the 13th Pacific Basin Nuclear Conference. Shenzhen, China, 2002.
( 0) 0)
|
| [12] |
JACKSON J D, FEWSTER J. Forced convection data for supercritical pressure fluids[M]. Manchester: Simon Engineering Laboratory, University of Manchester, 1975.
( 0) 0)
|
| [13] |
PETUKHOV B S, KRASNOSHCHEKOV E A, PROTOPOPOV V S. An investigation of heat transfer to fluids flowing in pipes under supercritical condition[J]. ASME international developments in heat transfer, 1961, 3: 569-578. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


