随着新技术不断应用于雷达领域,雷达体制也变得复杂,电子侦察设备需要分析的情景也愈来愈多,要解决的问题复杂度也愈来愈高,所面临的困难也愈来愈大[1-2]。因此,如何在复杂、密集交叠的雷达信号脉冲流中快速准确地分选出雷达辐射源信号,是当前信号分选的研究重点与难点。
为了应对复杂电磁环境,空军工程大学的赵喜贵[3]提出将蚁群算法和K-Means相结合易编程实现的聚类算法,为信号分选提供了新的思路;空军工程大学的陈维高[4]对网格聚类算法进行改进,提高了抗干扰能力,增加了分选系统的实时性;多伦多大学的Frey[5]提出应用仿射聚类算法,空军航空大学的张国毅[6]将其应用到雷达信号分选中,并应用在线处理和离线处理对数据进行合批处理。
当雷达参数有接近或存在部分脉冲叠加时,仅依靠测量值无法对需要聚类的雷达参数进行合理更新,这是因为当脉冲描述字落入2个簇类中心的交叠区域时,量测误差无法完全反应脉冲描述字与雷达参数(聚类中心)的真实关系。针对上述问题,本文提出一种基于联合概率数据关联的雷达信号分选方法,算法将脉冲描述字参数从测量域转换到概率域,将脉冲描述字与雷达参数的距离转换为关联概率,与雷达参数中心的距离就是参数中心值各个参数与检测到的脉冲描述字对应参数的差值,距离为欧式距离,通过关联概率来对落入关联门限内的雷达参数分别进行更新,以达到更好的聚类效果。
1 雷达参数概率模型及参数域变换 1.1 雷达参数概率模型雷达参数概率模型将雷达参数从量测域转化到概率域,通过关联概率来描述当前脉冲描述字与之前确认簇类的相关性。
雷达参数概率模型依据3个基本假设:
假设1 杂波普遍存在于参数测量取值域的中任意位置,并且没有规律,所以认为杂波在参数检测取值域中服从均匀分布。
假设2 采样检测到雷达信号参数会有量测噪声误差和过程噪声误差,但是这2种误差可以认为是服从正态分布的,所以参数测量值虽有误差,但脉冲描述字与真实值的误差在测量误差门限内服从正态分布。
假设3 在每一个采样时刻至多有一个脉冲描述字属于当前确认簇类,这个事件发生概率为PD。这是因为,当前采样周期中当前时刻的检测到的脉冲描述字可能是来自雷达的信号,也可能是杂波。
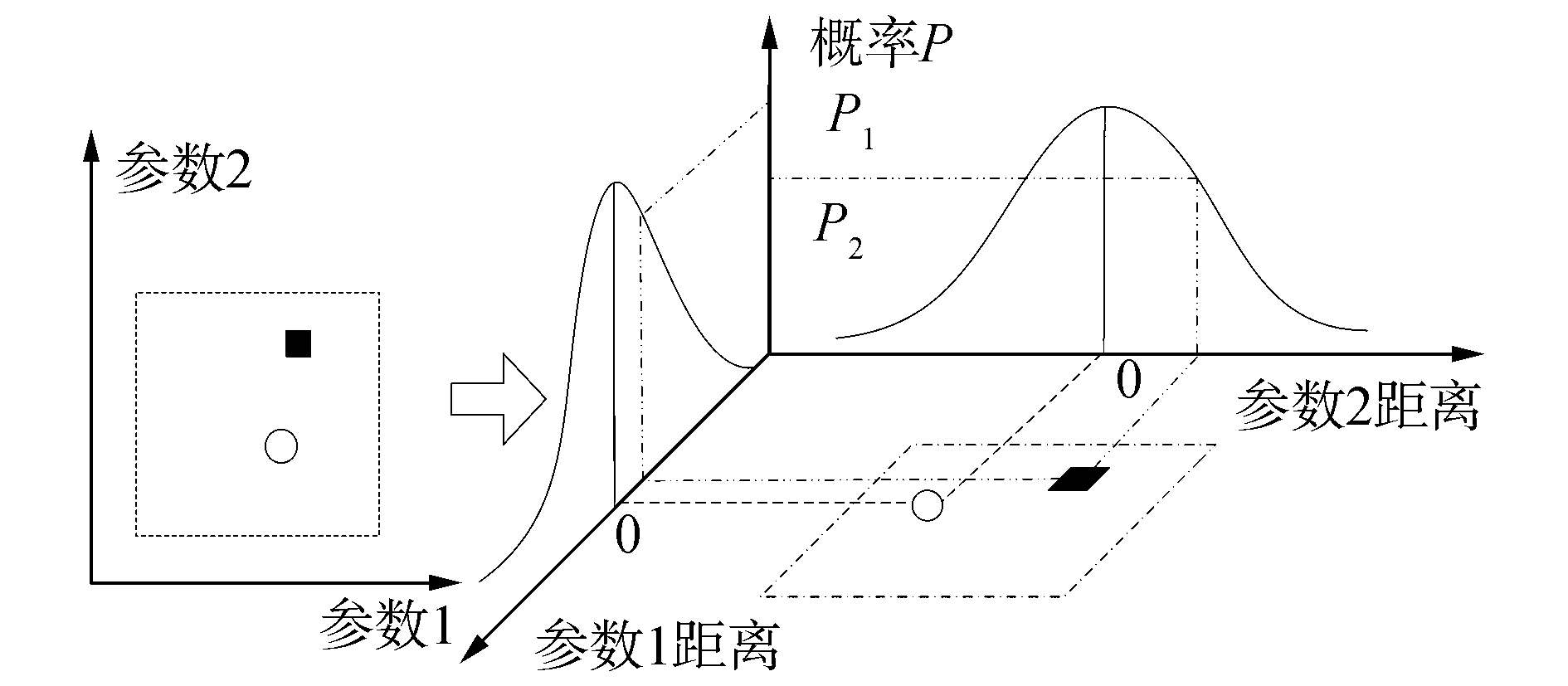
1.2 雷达信号参数域变换雷达信号参数域变换示意图如图 1所示。
|
Download:
|
| 图 1 雷达参数域变换示意 | |
假设分选用到两维参数分别为参数1、参数2,在量测域内检测到的脉冲描述字用黑色方块表示,雷达t的参数估计值用圆圈表示,虚线框表示关联门限,则根据参数在门限内的分布规律,脉冲描述字在雷达参数可能范围内服从高斯分布,图中的曲线为高斯分布概率密度曲线,将脉冲描述字参数与雷达参数的距离(量测误差)映射到概率密度曲线上的概率值P1和P2,实现雷达参数域变换。
2 雷达参数概率关联算法雷达参数概率关联模型用来描述脉冲描述字与不同的确认簇类的概率关系,也即描述脉冲描述字与之前得到的脉冲描述字的概率关系。
2.1 雷达信号聚类系统模型设复杂电磁环境下雷达t的状态方程为
| $ {\mathit{\boldsymbol{X}}^t}\left( {k + 1} \right) = \mathit{\boldsymbol{F}}\left( k \right){\mathit{\boldsymbol{X}}^t}\left( k \right) + \mathit{\boldsymbol{W}}\left( k \right) $ |
式中:k表示当前采样周期内第k个脉冲描述字被检测到,Xt(k)表示k时刻雷达t的参数真实值。
聚类过程中用到脉冲宽度(PW)、载频(FRE)、方位角(DOA)这三维参数。
| $ {\mathit{\boldsymbol{X}}^t}\left( k \right) = {\left[ {{\rm{P}}{{\rm{W}}^t}\left( k \right),{\rm{FR}}{{\rm{E}}^t}\left( k \right),{\rm{DOA}}\_{{\rm{A}}^t}\left( k \right)} \right]^\prime } $ | (1) |
式中PWt(k)、FREt(k)、DOA_At(k)分别表示k时刻雷达t的脉宽、载频、方位角的真实值。
F(k)表示k时刻的状态转移矩阵,在一个采样周期内检测到的同一部雷达信号用于聚类的脉冲描述字认为是一个常量,而不同的脉冲描述字参数间是相互独立的,F(k)为三阶单位阵,W(k)表示过程噪声,W(k)是零均值、白色高斯过程噪声序列,其协方差为Q(k),即E[W(k)W(j)]=Q(k)δkj,δkj为克罗内克函数(Kronecker delta)。
在一个采样周期内的k时刻,检测到的雷达信号t的检测方程为
| $ {\mathit{\boldsymbol{Z}}^t}\left( k \right) = \left\{ \begin{array}{l} \mathit{\boldsymbol{H}}\left( k \right){\mathit{\boldsymbol{X}}^t}\left( k \right) + V\left( k \right),雷达\;t\\ v\left( k \right),其他 \end{array} \right. $ |
式中:H(k)为代表量测矩阵,在这里是三阶单位阵;V(k)为具有协方差R(k)的零均值、白色高斯噪声序列,即E[V(k)V(j)]=R(k)δkj;υ(k)是在相关波门内均匀分布的杂波,或者来自其他雷达的脉冲描述字检测值。
假设k时刻雷达t的候选脉冲描述字为Zt(k),所有可能雷达的候选脉冲描述字集为Z(k),代表k时刻采样得到的脉冲描述字,当前采样周期中,直到k时刻确认雷达t和个确认簇类的脉冲描述字为Zt, k,直到k时刻累积得到的脉冲描述字集合为Zk。
由于一个采样周期内雷达参数是随时间微小变化的变量,在时变情况下,雷达参数中心最小均方误差估计值为
| $ {{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| k \right.} \right) = {\rm{E}}\left[ {{\mathit{\boldsymbol{X}}^t}\left( k \right)\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right] $ | (2) |
与式(2)相伴的误差协方差矩阵为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}^t}\left( {k\left| k \right.} \right) = }\\ {{\rm{E}}\left\{ {\left( {{\mathit{\boldsymbol{X}}^t}\left( k \right) - {{\hat X}^t}\left( {k\left| k \right.} \right)} \right){{\left( {{\mathit{\boldsymbol{X}}^t}\left( k \right) - {{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| k \right.} \right)} \right)}^\prime }\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right\}} \end{array} $ |
雷达t的一步预测为
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^t}\left( {k + 1\left| k \right.} \right) = E\left[ {{{\mathit{\boldsymbol{\hat X}}}^t}\left( {k + 1} \right)\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right] = }\\ {\mathit{\boldsymbol{F}}\left( k \right){{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| k \right.} \right)} \end{array} $ |
雷达t的新息协方差矩阵为
| $ {\mathit{\boldsymbol{S}}^t}\left( k \right) = \mathit{\boldsymbol{H}}\left( k \right){\mathit{\boldsymbol{P}}^t}\left( {k\left| {k - 1} \right.} \right)\mathit{\boldsymbol{H'}}\left( k \right) + \mathit{\boldsymbol{R}}\left( k \right) $ |
当某一时刻检测到的脉冲描述字同时满足落入不同雷达的关联门限时,需要综合考虑检测到的脉冲描述字的来源,并为其定义确认矩阵。为了表示当前时刻脉冲描述字与T部确认雷达信号的隶属关系,定义确认矩阵
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\left( k \right) = \left[ {{\omega _t}\left( k \right)} \right] = \overbrace {\left[ {\begin{array}{*{20}{c}} {{\omega _0}\left( k \right)}& \cdots &{{\omega _T}\left( k \right)} \end{array}} \right]}^T $ |
式中:ωt(k)=1表示k时刻采样得到的脉冲描述字落入雷达t(t=0, 1, …, T)的关联门内;ωt(k)=0表示k时刻得到脉冲描述字没有落到雷达t的关联内;t=0表示脉冲描述字来自杂波,ω0(k)=1是因为任何时刻得到的脉冲描述字都有可能来自干扰信号或杂波。
对确认矩阵Ω(k)进行拆分,得到可以涵盖确认矩阵中每种情况的联合事件θ(k),拆分后得到的矩阵称为联合矩阵
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\hat \varOmega} }}\left( {{\theta ^i}\left( k \right)} \right) = \left[ {\hat \omega _t^i\left( {{\theta ^i}\left( k \right)} \right)} \right] = }\\ {\overbrace {\left[ {\begin{array}{*{20}{c}} {\hat \omega _0^i\left( {{\theta ^i}\left( k \right)} \right)}& \cdots &{\hat \omega _T^i\left( {{\theta ^i}\left( k \right)} \right)} \end{array}} \right]}^T} \end{array} $ |
式中;
联合事件θi(k)的条件概率为
| $ \begin{array}{l} P\left\{ {{\theta ^i}\left( k \right)\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right\} = \frac{1}{{c'{V^{\varphi \left[ {{\theta ^i}\left( k \right)} \right]}}}}{N_t}\left[ {\mathit{\boldsymbol{Z}}\left( k \right)} \right]\tau \left[ {{\theta ^i}\left( k \right)} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\prod\limits_{t = 1}^T {{{\left( {P_D^t} \right)}^{{\delta _t}\left[ {{\theta ^i}\left( k \right)} \right]}}{{\left( {1 - P_D^t} \right)}^{1 - {\delta _t}\left[ {{\theta ^i}\left( k \right)} \right]}}} \end{array} $ |
当δt[θi(k)]为“1”时,表示在联合事件θi(k)中,一部已经确认的雷达t与当前的脉冲描述字相关联,即雷达t被关联;“0”则表示不关联。τ[θi(k)]为“1”表示在联合事件θi(k)中,一部已经确认的雷达与当前的脉冲描述字相关联,而“0”则表示不关联。Nt[Z(k)]表示Z(k)服从均值是Ẑt(k|k-1)方差是St(k)的高斯分布的概率密度值,c′表示归一化常数。
2.3 关联概率的计算设ϑt(k)表示k时刻检测到的脉冲描述字是与雷达t关联的事件,事件ϑ0(k)表示检测到的脉冲描述字是杂波。
以直到k时刻的累积脉冲描述字流的集合为条件,k时刻检测到的脉冲描述字与雷达t关联的条件概率为
| $ \begin{array}{*{20}{c}} {{\beta _t}\left( k \right) = P\left\{ {{\vartheta _t}\left( k \right)\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right\} = }\\ {\sum\limits_{i = 1}^{{n_k}} {\hat \omega _t^i\left[ {{\theta ^i}\left( k \right)} \right]P\left\{ {{\theta ^i}\left( k \right)\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right\}} } \end{array} $ |
聚类中心的更新根据互联概率来计算,k时刻确认雷达t的参数估计值为
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| k \right.} \right) = {\rm{E}}\left[ {{X^t}\left( k \right)\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right] = }\\ {\left( {1 - {\beta _t}\left( k \right)} \right)\mathit{\boldsymbol{\hat X}}_0^t\left( {k\left| k \right.} \right) + {\beta _t}\left( k \right)\mathit{\boldsymbol{\hat X}}_1^t\left( {k\left| k \right.} \right) = }\\ {\left( {1 - {\beta _t}\left( k \right)} \right){{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| {k - 1} \right.} \right) + {\beta _t}\left( k \right)\hat X_1^t\left( {k\left| k \right.} \right)} \end{array} $ |
式中:
| $ \mathit{\boldsymbol{\hat X}}_1^t\left( {k\left| k \right.} \right) = {{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| {k - 1} \right.} \right) + {\mathit{\boldsymbol{K}}^t}\left( k \right){v^t}\left( k \right) $ |
Kt(k)是雷达t的卡尔曼滤波[11, 15]增益矩阵,在这里是3阶对角阵,其中的非零元素表示雷达三维参数的增益,vt(k)是雷达t的新息,即量测值与预测值之间的差值。
雷达t的参数估计误差协方差更新矩阵表达式为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}^t}\left( {k\left| k \right.} \right) = {\mathit{\boldsymbol{P}}^t}\left( {k\left| {k - 1} \right.} \right) - {\beta _t}\left( k \right){\mathit{\boldsymbol{K}}^t}\left( k \right){\mathit{\boldsymbol{S}}^t}\left( k \right){\mathit{\boldsymbol{K}}^t}^\prime \left( k \right) + }\\ {\left( {1 - {\beta _t}\left( k \right)} \right){{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| {k - 1} \right.} \right){{\mathit{\boldsymbol{\hat X}}}^t}^\prime \left( {k\left| {k - 1} \right.} \right) + }\\ {{\beta _t}\left( k \right)\mathit{\boldsymbol{\hat X}}_1^t\left( {k\left| {k - 1} \right.} \right)\mathit{\boldsymbol{X}}{{_1^t}^\prime }\left( {k\left| {k - 1} \right.} \right) - }\\ {{{\mathit{\boldsymbol{\hat X}}}^t}\left( {k\left| k \right.} \right){{\mathit{\boldsymbol{\hat X}}}^t}^\prime \left( {k\left| k \right.} \right)} \end{array} $ |
聚类中心在雷达参数初始化后,每得到一个脉冲描述字进行一次更新。更新后的聚类中心,协方差用于下一次关联概率的计算,及下一次聚类中心、协方差的更新。
相关矩阵表示当前脉冲描述字与不同确认簇类的相关性,其表达式为
| $ \beta \left( k \right) = \left[ {{\beta _1}\left( k \right),{\beta _2}\left( k \right), \cdots ,{\beta _T}\left( k \right)} \right] $ |
矩阵中每个元素是脉冲描述字与不同簇类的关联概率。
3 算法流程雷达参数概率关联算法的流程主要分为2部分:第1部分,雷达参数初始化,初始化的过程是对检测到的脉冲描述字形成确认簇类,也就是确认雷达初始化的过程;第2个部分是雷达参数更新过程,也就是当脉描述字落入确认雷达关联门限时,利用雷达参数概率模型,对雷达参数进行更新,也就是聚类中心的更新过程。
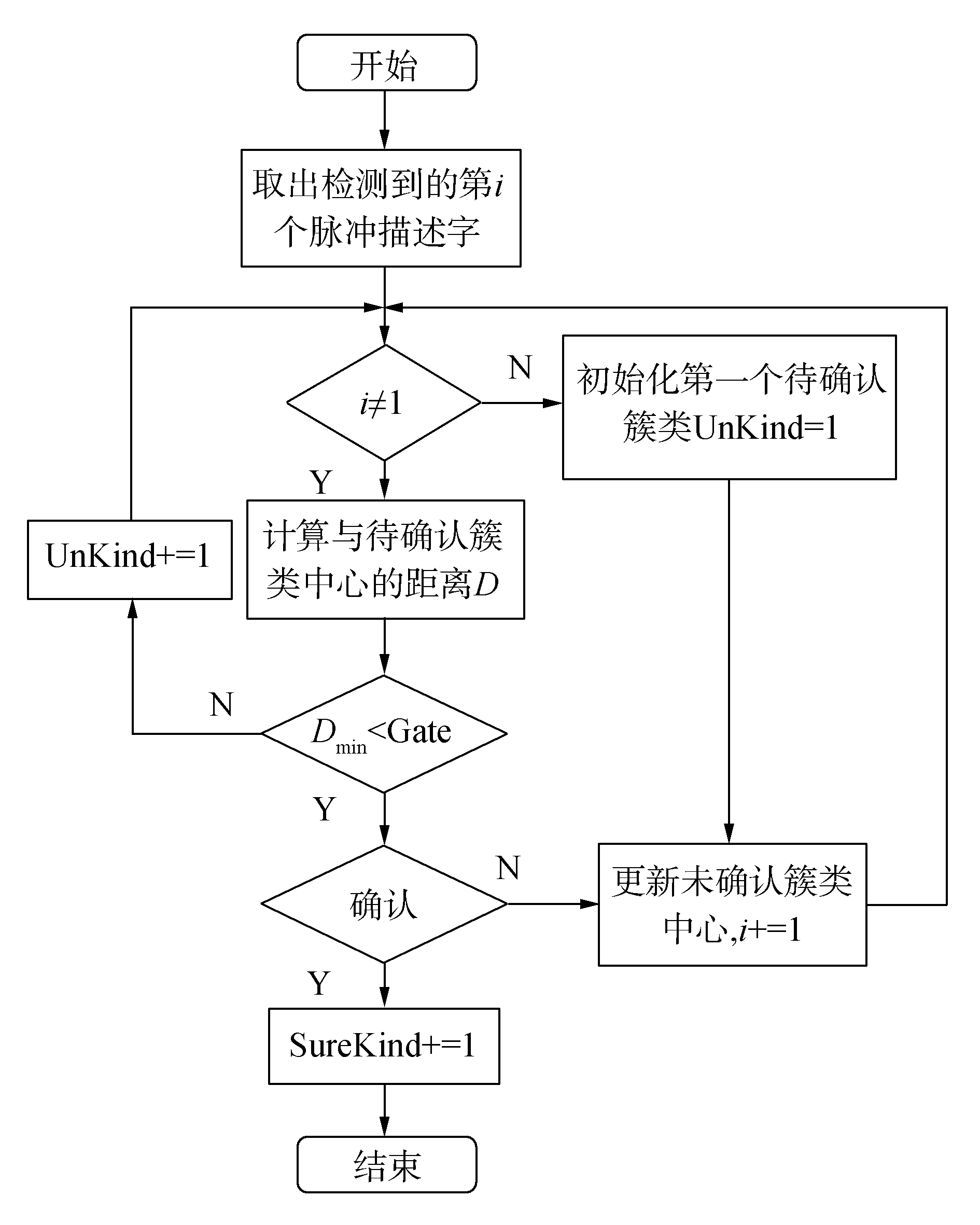
3.1 雷达参数初始化流程雷达参数初始化使用改进的K-Means算法初始化确认雷达,与传统K-Means算法[12-13]相比,不再限定聚类的个数,而是限定数据与聚类中心的终止条件,雷达参数初始化流程图如图 2所示。
|
Download:
|
| 图 2 雷达参数初始化流程 | |
具体步骤为:
1) 算与每个待确认簇类中心的距离;
2) 判断最小距离Dmin是否小于门限Gate,如果小于门限,则判断当前簇类中脉冲描述字的个数是否满足确认条件,否则,转到步骤1),进行下一个脉冲描述字的判断;
3) 如果满足确认条件,即当前簇类下脉冲描述字个数大于最小确认值,则此簇类得到确认,否则算法结束。
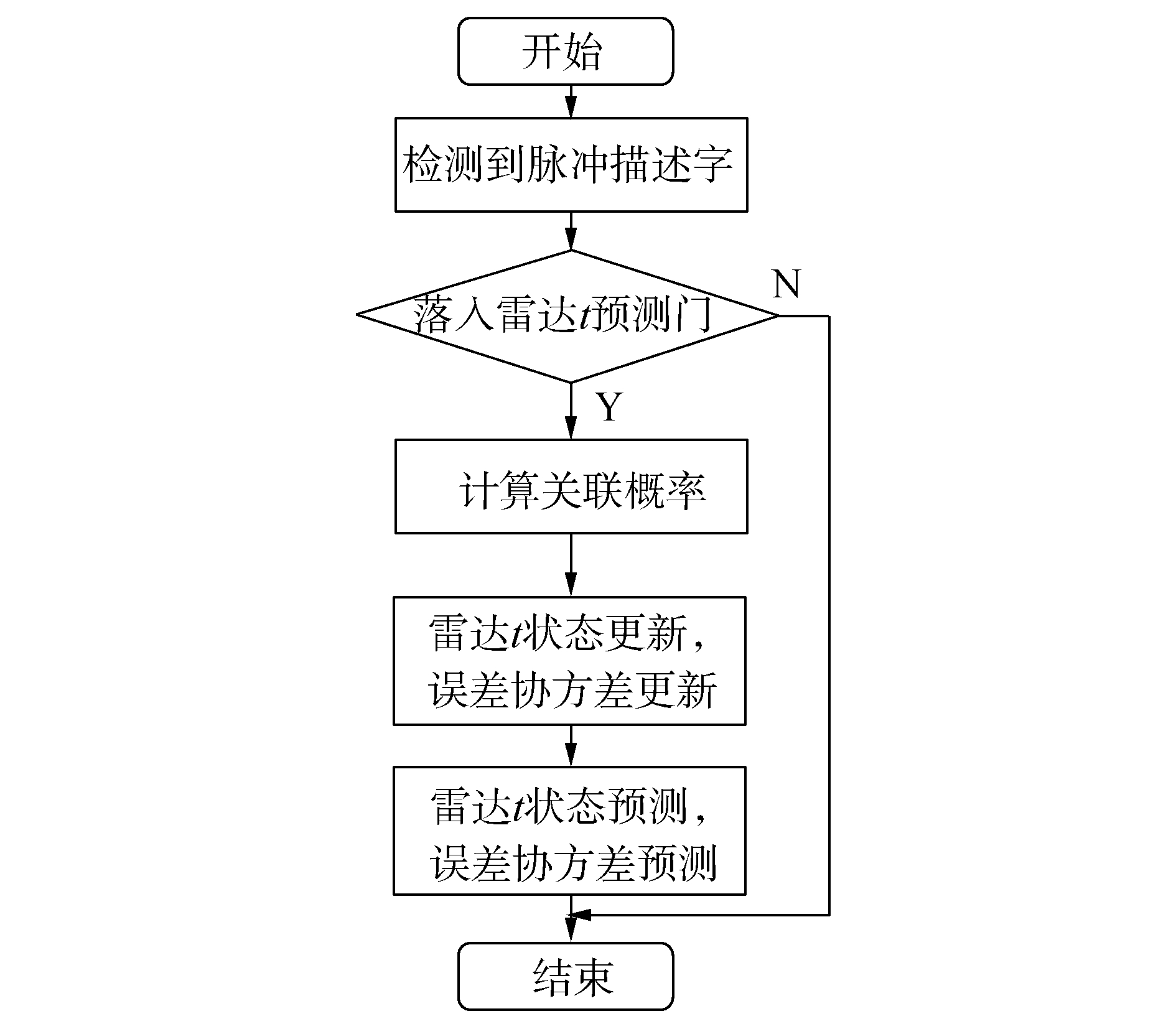
3.2 雷达参数更新流程雷达参数更新流程图如图 3所示。
|
Download:
|
| 图 3 雷达参数更新流程 | |
1) 判断检测到的脉冲描述字是否落入雷达t的关联门限,如果落入,转到步骤2),如果没落入,不对雷达t的参数进行更新;
2) 利用雷达参数关联模型,对雷达t的状态参数进行更新,误差协方差进行更新,也就是可能的聚类中心更新;
3) 对雷达t的状态做进一步的预测,同时预测误差协方差;
4) 结束本次更新。
4 算法仿真 4.1 雷达参数聚类算法仿真分析与对比设定当前环境中存在12部雷达信号,如表 1所示,其中包含编号1~5为PRI固定雷达信号;编号8~10为参差PRI雷达信号,括号中代表子PRI;编号6~7为抖动PRI雷达信号,括号中代表抖动率;编号11~12为捷变频雷达信号,表格中频率代表跳变的频点。包括参数相近/交叠的雷达信号,对400 ms内检测到的信号用基于雷达参数概率模型的聚类算法进行仿真分析。其中脉宽的精度是0.1 μs,载频的精度是1 MHz,方位角的精度是1°,即数据误差的3倍标准差为精度值,门限值设置为6倍标准差,存在脉冲叠加,以及杂波10%,无脉冲丢失。从表 1中可以看出,雷达编号7和编号11有参数相近的部分,为了观测更加直观,对所有的数据都进行归一化处理,归一化采用Max-Min标准化处理,归一化公式如式(3)所示。
|
|
表 1 雷达参数设置表格 |
| $ {\rm{dat}}{{\rm{a}}_{{\rm{norm}}}} = \frac{{\left( {{\rm{dat}}{{\rm{a}}_{{\rm{orig}}}} - {\rm{dat}}{{\rm{a}}_{{\rm{min}}}}} \right)}}{{{\rm{dat}}{{\rm{a}}_{{\rm{max}}}} - {\rm{dat}}{{\rm{a}}_{{\rm{min}}}}}} $ | (3) |
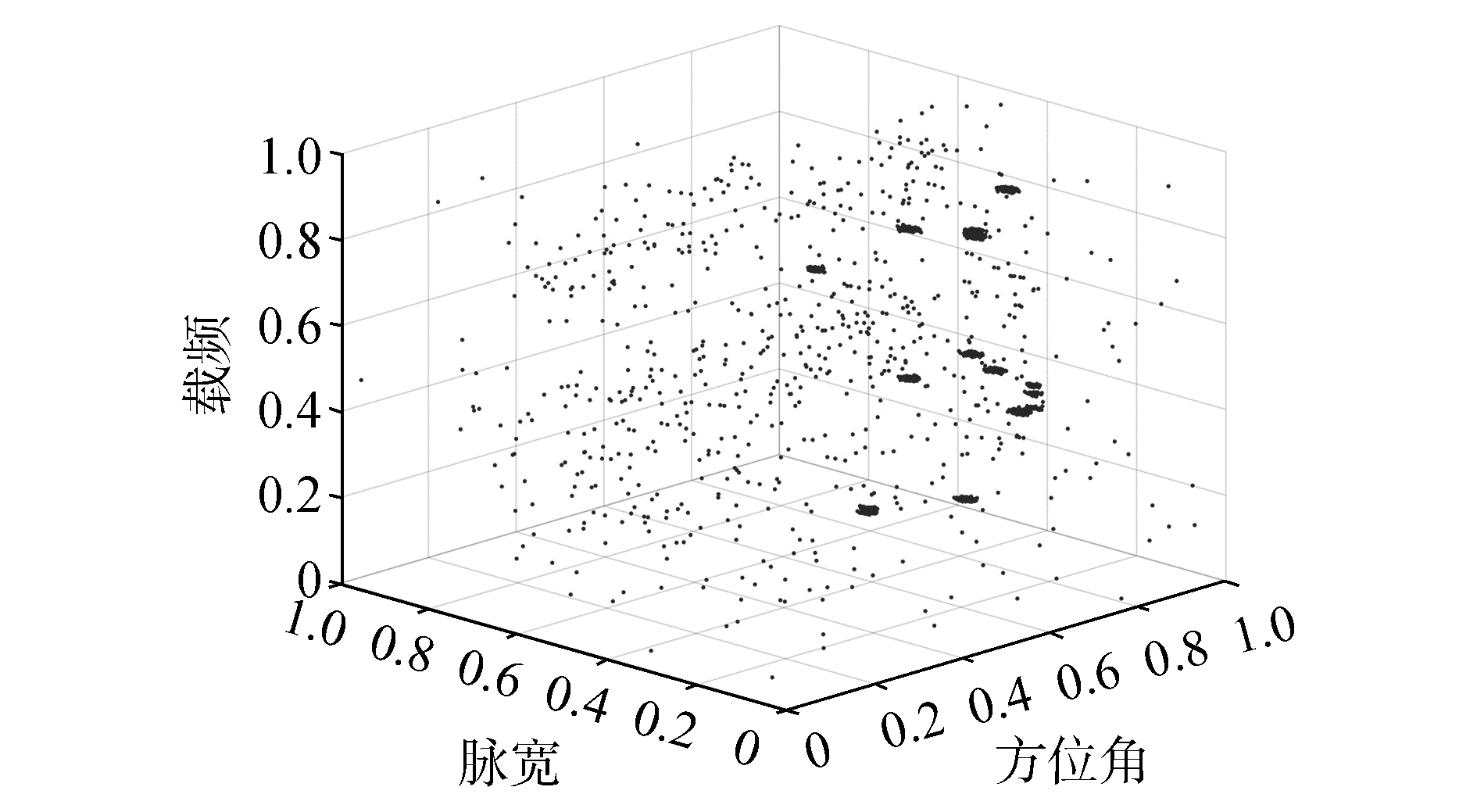
式中:dataorig为一个采样周期中得到的某个脉冲描述字的参数值,datamax为采样中得到的脉冲描述字参数的最大值,datamin为采样中得到的脉冲描述字参数的最小值,datanorm为原始数据归一化后得到的参数值。输入的待分选关联数据分布如图 4所示。
|
Download:
|
| 图 4 归一化的待聚类雷达信号 | |
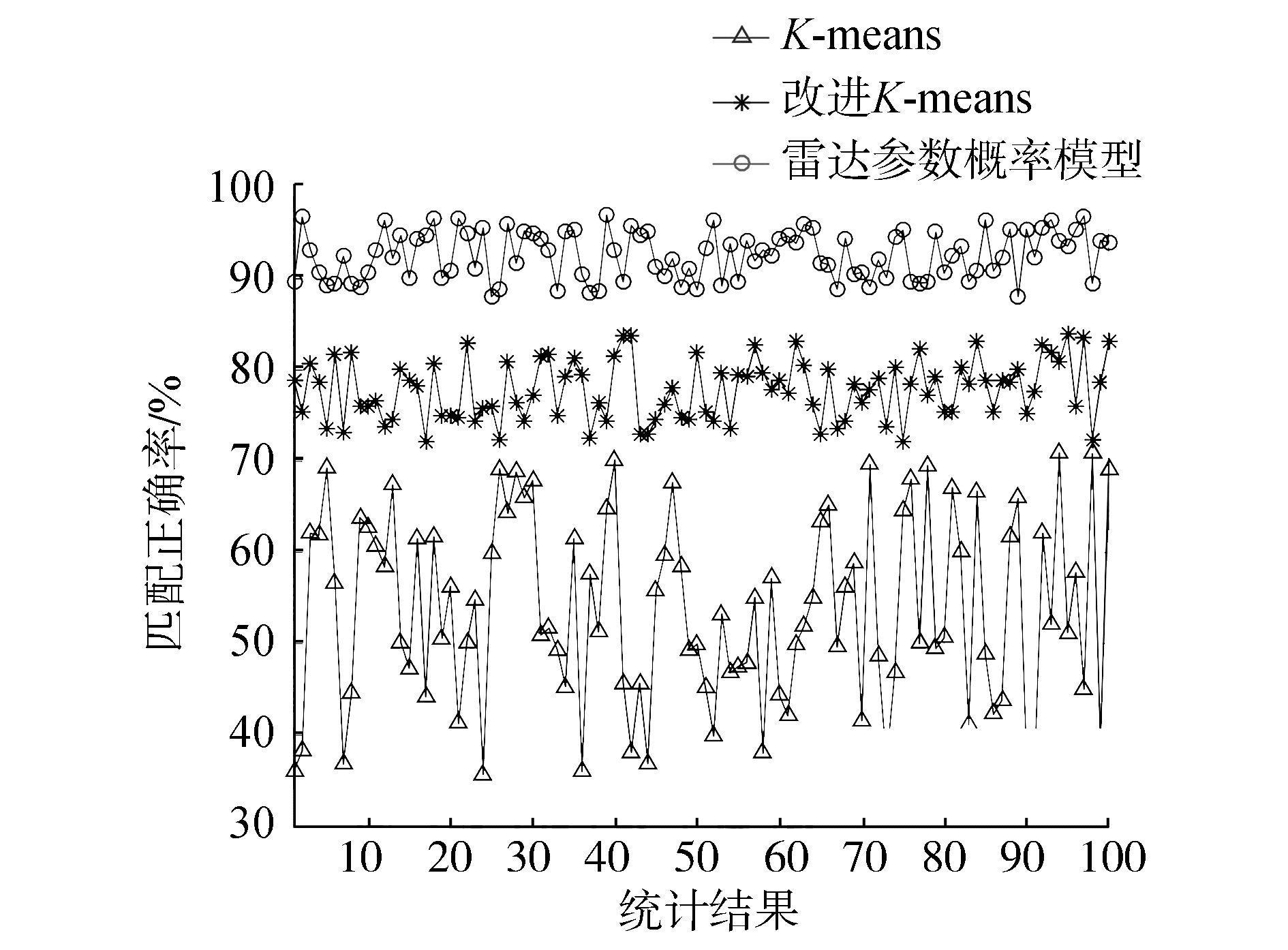
使用表 1中的数据,通过100次蒙特卡洛试验。用K-Means、改进的K-Means和基于雷达参数概率模型算法对数据进行聚类,分选后得到的类别个数为15个,其中捷变频雷达被按照载频分成了多部,这符合真实情况,平均正确匹配率如图 5所示。图中正确匹配率表示采用聚类结果的正确匹配率的平均值作为当次蒙特卡洛试验的平均正确匹配率。其中正确匹配率表示被正确归类的脉冲个数占比。表达式为
| $ {\eta _m} = \frac{{{\rm{Nclu}}}}{{{\rm{Num}}}} $ |
|
Download:
|
| 图 5 与K-Means算法比较 | |
设定电磁环境中存在某部雷达Radarm,Num表示一个采样周期内检测到的脉冲描述字中属于雷达Radarm的脉冲个数,Nclu表示聚类后,得到的属于雷达Radarm的脉冲的个数。
由图 5可以得出,K-Means由于初始聚类中心选取对结果的影响较大,平均正确匹配率波动性较大。聚类中心随机选择,难以保证每个雷达信号都能作为初始聚类中心,此外,杂波干扰对聚类的结果影响较大,导致无法形成全局最优解,仅仅局部最优解。改进K-Means算法平均正确匹配率变化较小,聚类效果较为稳定,平均正确匹配率在79%左右,而雷达参数概率模型算法平均正确匹配率在94%左右,聚类效果最好。
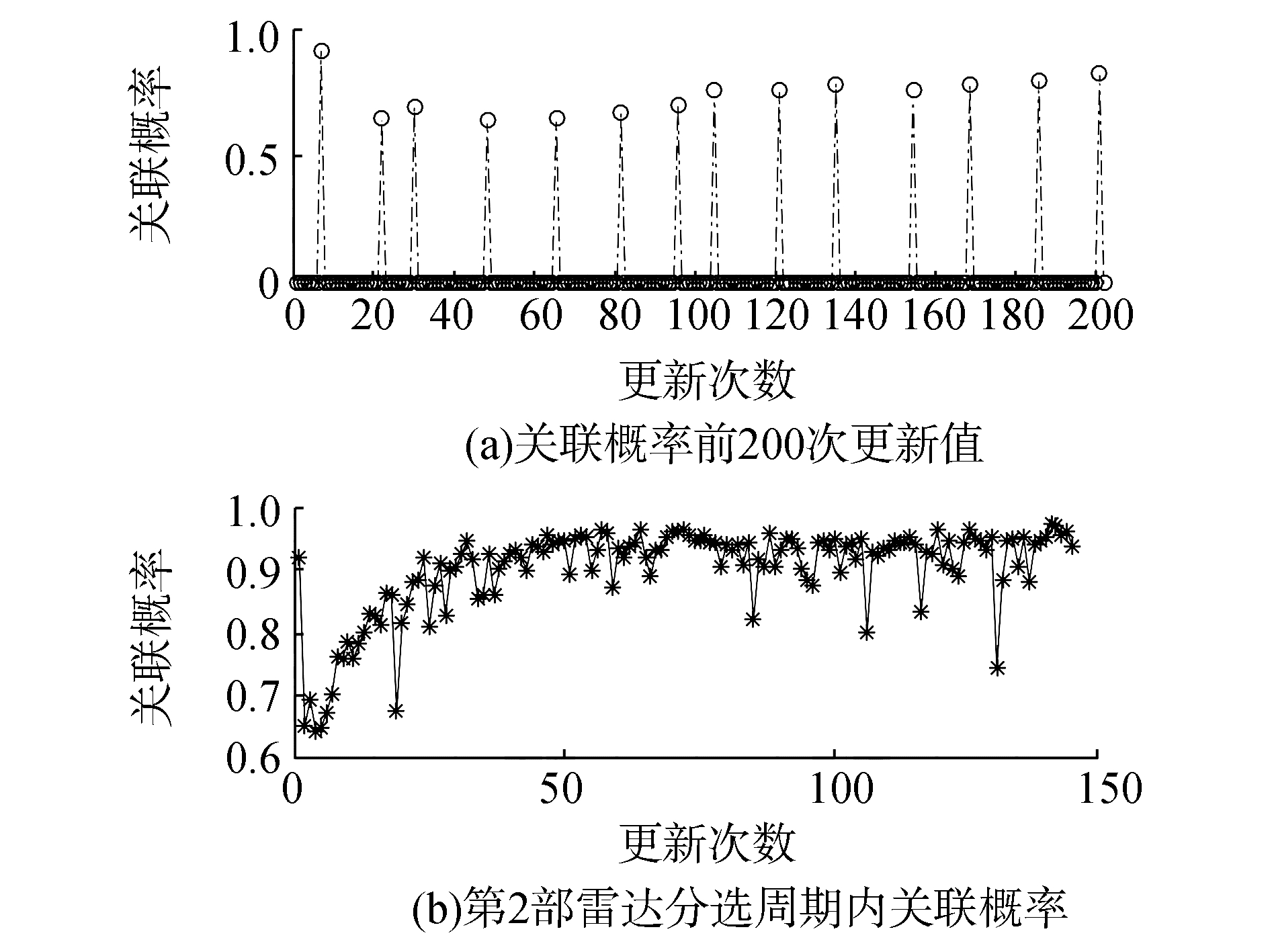
以表 1中第2部雷达的分选过程为例,其关联概率随更新次数的变化值如图 6所示。图 6(a)截取了更新过程的前200次关联概率值,从图中可以看出,关联概率是时变的,当关联概率为0时说明脉冲描述字与第2部雷达的参数中心没有关联上,当关联概率不为0时,说明脉冲描述字与第2部雷达的参数中心关联上;图 6(b)是一个分选周期该雷达非零关联概率的值,从下半部分可以看到,非零的关联概率也是随聚类中心的更新不断变化的,在初始的几次更新中,波动较大,后期相对稳定。
|
Download:
|
| 图 6 关联概率随更新次数变化 | |
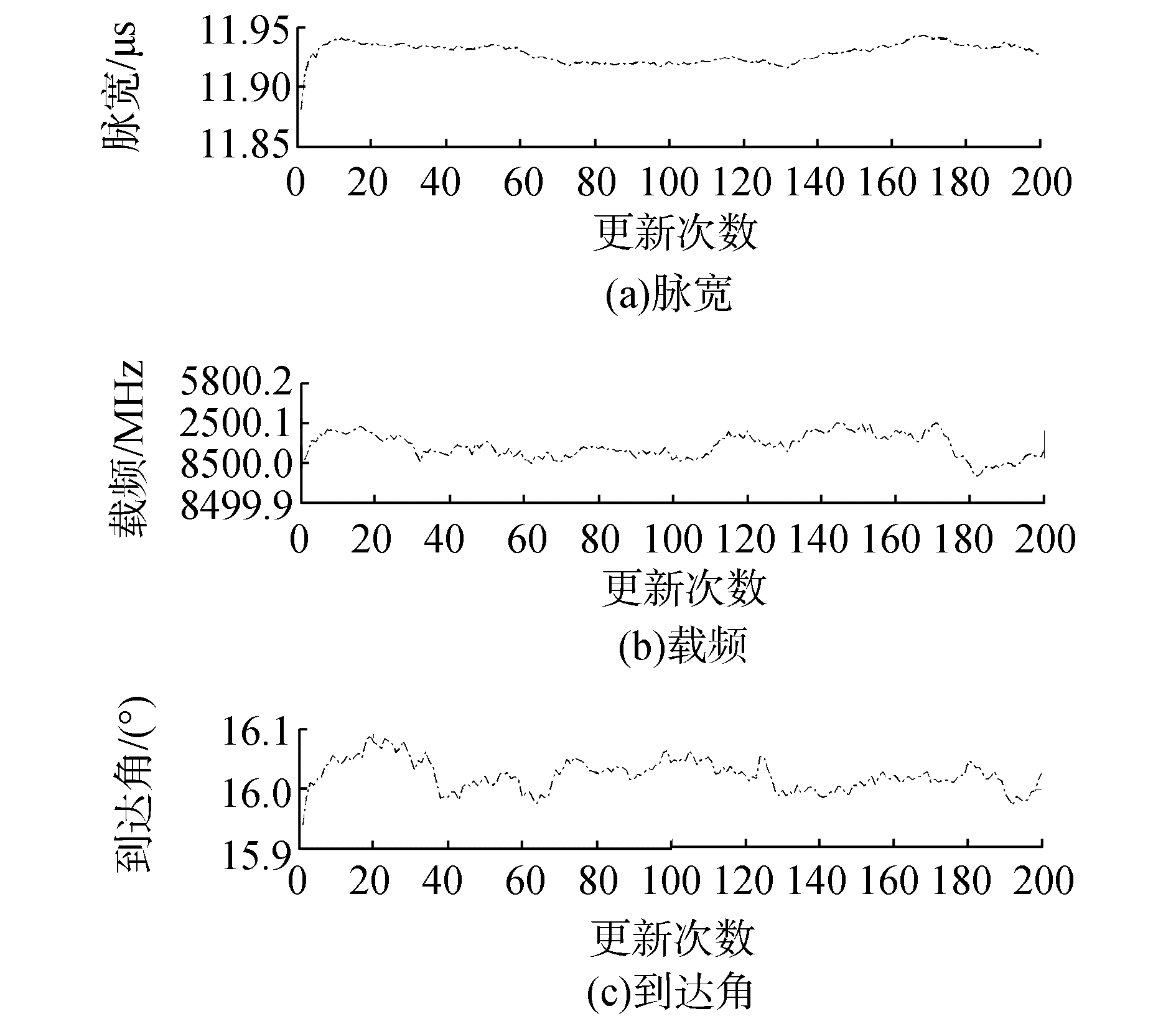
通过蒙特卡洛仿真能够发现,在极少数的情况下,雷达信号参数模型会将本来归属为1部雷达的脉冲描述字分成2个子类,出现这种情况的原因是每个聚类中心更新过程中考虑了一个脉冲描述字同时与多部确认雷达进行关联的关联概率,但是在聚类中心更新的过程中,可能会出现更新值远离真实的雷达参数中心的情况,从而导致在一些循环更新后,将1个簇类分成2个子类的情况。针对这种情况,进行仿真实验,判断迭代几次后算法的聚类中心收敛,不再出现偏离真实中心值太远的情况。以表 1中第2部雷达为例,观察每次聚类中簇类中心的更新情况,用100次蒙特卡洛仿真的均值画图,取迭代次数前200的情况进行观察。结果如图 7所示。
|
Download:
|
| 图 7 聚类中心收敛速度图 | |
从图 7可以看出,聚类中心在更新10次左右的时候,趋于稳定的状态,之后的变化都是在测量误差允许的范围内极小范围的波动,没有出现参数大范围抖动的情况,说明应用此算法进行聚类的效果稳定性较好,准确性较好。
5 结束语本文提出了基于联合概率关联算法的雷达参数概率模型聚类算法。首先介绍了雷达参数概率模型及雷达参数域变换的必要性,其次介绍了雷达参数概率关联算法,包括关联概率计算、聚类中心更新及协方差更新的过程以及雷达参数初始化的过程,再次介绍聚类模型的处理流程,最后对雷达参数概率模型进行仿真,并与传统的聚类算法进行对比,分析算法的仿真效果。经试验表明,本算法在面对电磁环境中存在雷达参数相近或部分交叠,且存在杂波的情况下,能够进行信号聚类,平均正确匹配率为94%左右。算法稳定性好,具备良好的聚类性能。
| [1] |
梁华东, 韩江洪. 基于维格纳分布特征的雷达信号分选[J]. 电子测量与仪器学报, 2014, 28(2): 218-225. ( 0) 0)
|
| [2] |
贺平. 雷达对抗原理[M]. 北京: 国防工业出版社, 2016.
( 0) 0)
|
| [3] |
赵贵喜, 骆鲁秦, 陈彬. 基于蚁群算法的K-Means聚类雷达信号分选算法[J]. 雷达科学与技术, 2009, 7(2): 142-146. DOI:10.3969/j.issn.1672-2337.2009.02.014 ( 0) 0)
|
| [4] |
陈维高, 张国毅. 基于改进网格聚类的动态雷达信号分选算法[J]. 雷达与对抗, 2012, 32(4): 30-34, 46. ( 0) 0)
|
| [5] |
FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976. DOI:10.1126/science.1136800 ( 0) 0)
|
| [6] |
刘志鹏, 张国毅. 一种新的雷达信号实时分选方法[J]. 航天电子对抗, 2016, 32(2): 6-9, 17. DOI:10.3969/j.issn.1673-2421.2016.02.002 ( 0) 0)
|
| [7] |
耿利祥, 陈钱, 钱惟贤. 改进的联合概率数据关联算法(JPDA)对红外目标与诱饵的辨别[J]. 红外与激光工程, 2013, 42(2): 305-310. DOI:10.3969/j.issn.1007-2276.2013.02.006 ( 0) 0)
|
| [8] |
FORTMANN T, BAR-SHALOM Y, SCHEFFE M. Sonar tracking of multiple targets using joint probabilistic data association[J]. IEEE journal of oceanic engineering, 1983, 8(3): 173-184. DOI:10.1109/JOE.1983.1145560 ( 0) 0)
|
| [9] |
STREIT R. JPDA intensity filter for tracking multiple extended objects in clutter[C]//201619th International Conference on Information Fusion. Heidelberg, Germany, 2016: 1477-1484.
( 0) 0)
|
| [10] |
REZATOFIGHI S H, MILAN A, ZHANG Zhen, et al. Joint probabilistic data association revisited[C]//2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 3047-3055.
( 0) 0)
|
| [11] |
WELCH G, BISHOP G. An introduction to the Kalman filter[D]. Carolina: University of North Carolina at Chapel Hill, 2001.
( 0) 0)
|
| [12] |
张阳, 何丽, 朱颢东. 一种改进的K-Means动态聚类算法[J]. 重庆师范大学学报(自然科学版), 2016, 32(1): 97-101. ( 0) 0)
|
| [13] |
王越, 王泉, 吕奇峰, 等. 基于初始聚类中心优化和维间加权的改进K-Means算法[J]. 重庆理工大学学报(自然科学版), 2013, 27(4): 77-80. DOI:10.3969/j.issn.1674-8425(z).2013.04.016 ( 0) 0)
|
| [14] |
黄辰. 几种典型聚类方法在雷达信号分选中的应用浅析[J]. 电子信息对抗技术, 2017, 32(5): 1-4, 62. DOI:10.3969/j.issn.1674-2230.2017.05.001 ( 0) 0)
|
| [15] |
STUBBERUD S C, KRAMER K A. Monitoring the Kalman gain behavior for maneuver detection[C]//201725th International Conference on Systems Engineering. Las Vegas, USA, 2017: 39-44.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


