医学超声是将声学、医学和电子设备相结合的一门学科,分为医学诊断和医学治疗。医学诊断根据超声波在人体的传播过程中与组织的相互作用,包括信号的衰减、反射及透射等,从接收信号中提取能够反映组织状况的信息。超声诊断具有简便快捷、无创无损无辐射、实时性的优点。
常见的超声诊断通常采用反射法,实际上回波是不确定的信号,高质量的信号分析不能仅使用反射数据重建[1]。与回波信号相比,透射信号受到的组织内的随机因素影响较小,其幅值的变化遵循生物组织的超声衰减规律,可以作为一种确定性信号,结果比较精确。2003年Mohamed等[2]利用超声透射法测量了牛松质骨中的声速,实验结果与预测值的相关性大于0.86。2006年吕海涛[3]对生物组织的衰减系数分别采用反射法、透射法测量,经过数据对比,透射法测量得到的衰减系数与理论值更接近。2014年Oliveira等[4]采用超声透射法对三组软组织模拟物的衰减系数进行测量,结果表明其测量衰减值与软组织相容。2015年,Abderrazek[5]通过超声透射法测量骨样品的超声衰减系数。
根据超声波在生物组织中的透射传播规律,分析超声在生物组织作用下的传输衰减,包括黏滞性、热传导、散射衰减,整合出用于分析超声衰减与频率以及生物组织特性参数的相关性的公式。针对超声衰减与频率以及生物组织特性的关系,设计仿真与实验,结果表明该理论计算公式可靠有效。同时基于超声透射法的谱分析对于组织的辨识度高,通过接收波形可以判断组织的厚度以及其状态,可以很好地应用于对生物组织状态的分析,提高超声诊断的准确性。
1 超声传播方程及组织模型 1.1 传播方程理想介质的一维空间中,压强p的波动方程为
| $ {\nabla ^2}p = \frac{1}{{{c^2}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} $ |
式中c为组织的声速。
在医学超声的背景下,对于理想介质中波动方程的求解采用余弦波点声源、零初始值和无反射边界条件[6]。求得超声波在理想介质中传播的数学表达式为:
| $ p\left( {t,x} \right) = {p_0}\cos \left( {\omega t - kx} \right) $ |
式中:ω为声波的角频率;k为波束,k=ω/c。
考虑介质的黏滞性,超声波的运动方程表示为
| $ \rho \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - \frac{{{\rm{d}}p}}{{{\rm{d}}x}} + \mu \frac{{{\rm{d}}v}}{{{\rm{d}}x}} $ |
式中μ为介质的黏滞项。
波动方程变为
| $ \frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{\mu }{B}\frac{{{\partial ^2}p}}{{\partial x\partial t}} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} = 0 $ |
上述方程的近似解为
| $ p\left( {t,x} \right) = {p_0}\cos \left( {\omega t - kx} \right)\exp \left( { - {\alpha _\eta }x} \right) $ |
式中αη是由μ和B、ω决定的常数,是介质的黏滞性对超声产生的衰减项。
考虑软组织的吸收、散射作用对超声传播产生的衰减。当发射声压为P0、超声波传播距离为x时,声波的变化可表示为[7]
| $ P = {P_0}\exp \left( { - \alpha x} \right) $ |
式中α表示超声在软组织中的衰减系数。
α值的获取一般通过实验来测得,缺乏系统的理论分析。本文考虑软组织的衰减特性,对α值通过公式进行计算,用于对组织状态的理论分析。
1.2 仿真模型本文建立的生物组织仿真模型的尺寸为5 cm×5 cm×5 cm,考虑到生物组织对超声具有吸收、散射作用,图 1为生物软组织模型图,图中圆圈表示组织中的散射子。
|
Download:
|
| 图 1 生物软组织模型 | |
超声衰减是指超声在介质中传播发生了能量损失。超声在软组织中的传输衰减主要是由于软组织的吸收、散射作用引起的吸收衰减和散射衰减[8]。吸收衰减包括黏滞性、热传导以及驰豫衰减。本节研究并分析软组织的吸收、散射作用,以及频率对超声衰减的影响,其相关性通过公式表达,对各类衰减进行汇总,得到整体的衰减系数表达式。进行仿真实验,将实验值与理论值相比较,结果表明本文衰减公式是可用的,同时可以了解到各参数对衰减的作用。
1) 黏滞衰减
由上节可知,当介质具有黏滞性时,超声在传播过程中产生一个衰减项。生物组织本身具有的黏滞性使组织之间发生内摩擦,使得超声波的能量在传播过程中发生衰减。超声波的黏滞衰减系数公式为[9]:
| $ {\alpha _\eta } = \frac{{{w^2}\eta }}{{2\rho {c^3}}} = \frac{{2{{\rm{ \mathsf{ π} }}^2}{f^2}}}{{\rho {c^3}}}\left( {\frac{4}{3}{\eta _1} + {\eta _2}} \right) $ |
式中:η1、η2分别为切边黏滞系数、容变黏滞系数,Pa·s;f为超声波的频率,Hz;ρ为密度,kg/m3; c为声速,m/s。
2) 热传导衰减
热传导是软组织中温度较高区域与温度较低区域的分子之间能量交换的过程。在交换过程中,超声波会发生能量的损失。热传导的衰减系数为:
| $ {\alpha _\xi } = \frac{{{w^2}\chi }}{{2\rho {c^3}}}\left( {\frac{1}{{{c_v}}} - \frac{1}{{{c_p}}}} \right) $ |
式中:χ为热传导系数,W/m·℃; cv为介质的定容比热,J/kg·℃;cp为介质的定压比热,J/kg·℃;k=cp/cv,k为介质的定热比率。
3) 驰豫衰减
驰豫过程是在一定的状态下,软组织中分子的内外自由度重新分配达到新的平衡状态的过程。分配的过程会使声波能量产生损耗。驰豫衰减为
| $ {\alpha _R} = \frac{{{w^2}}}{{2\rho {c^3}}}\frac{{\eta _0^ * }}{{1 + {w^2}{{\tau '}^2}}} $ |
式中:
当声波频率甚高时,驰豫过程甚短,可以不予考虑。本文采用1~5 MHz的高频声波,所以此处的驰豫衰减可以忽略不计。
4) 散射衰减
超声波在组织中传播时,遇到颗粒或者界面会使部分声波的方向发生改变,不能到达接收器,这种现象称为散射衰减。在理论研究中,将这些散射粒子等效为半径为r的刚性球体。散射衰减系数αs为
| $ {\alpha _s} = \frac{8}{9}{\rm{ \mathsf{ π} }}{k^4}{r^6}n $ | (1) |
式中:k为超声波波束,k=w/c; r为散射粒子半径; n为单位体积内粒子数目。
对于软组织的高斯散射模型,散射系数为
| $ {\alpha _s} = 0.827{\left( {2{\rm{ \mathsf{ π} }}f/c} \right)^2}{r^2} $ | (2) |
由此可知,衰减系数α等于黏滞衰减系数αη、热传导衰减系数αξ、散射衰减系数αs之和
| $ \alpha = {\alpha _\eta } + {\alpha _\xi } + {\alpha _s} $ | (3) |
α的单位可用dB·cm-1·MHz-1表示,也可以用NP·cm-1·MHz-1表示,它们之间关系1 NP·cm-1·MHz-1=8.686 dB·cm-1·MHz-1。
衰减系数α的计算需要选取合理可靠地特性参数以保证计算结果的有效性、准确性。特性参数的选取如表 1[10]。
|
|
表 1 组织的特性参数值 |
将表 1所示参数带入式(3),计算得到超声在软组织传播过程中的各类型衰减值,以及总衰减系数。软组织的衰减系数α的公认值为0.81 dB·cm-1·MHz-1,也有文献采用0.5~0.6 dB·cm-1·MHz-1,本文在计算过程中忽略了驰豫衰减以及其他客观因素的影响,计算值比公认值偏低一些,接近度仍达到74.1%。声波在组织中的散射衰减仅占整个衰减的百分之几[11],该计算中散射衰减占总衰减的5%。由此可知,该整合公式的计算值符合软组织衰减系数的实验值,可以用来表示超声在软组织传播过程中的衰减情况的理论分析。表 2为计算结果。
|
|
表 2 计算结果 |
α与频率f的关系为[12]:
| $ \alpha = {\alpha _0}{\left( {f/{f_0}} \right)^n} $ | (4) |
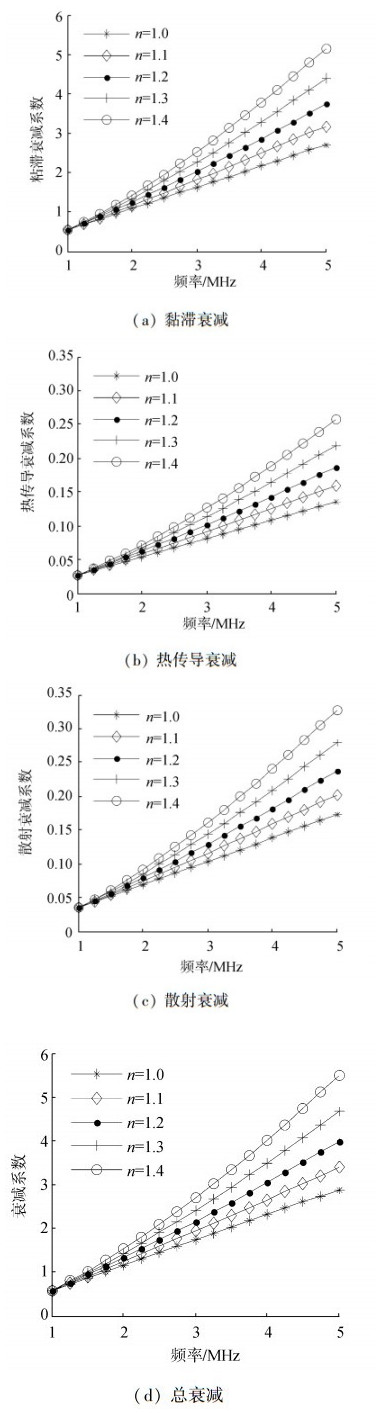
式中:α0为频率f0时的衰减系数,本文取α0为f0=1 MHz时的衰减系数;n为衰减的频率依赖指数,取值一般在1~1.4之间。当n取不同值时,衰减系数随频率的变化如图 2、3所示。
|
Download:
|
| 图 2 n取不同值时,衰减系数随频率变化情况 | |
|
Download:
|
| 图 3 衰减系数随频率变化情况 | |
由图 2、3可知,随着n的增大,衰减系数对频率的依赖性也越大,在1~1.4之间,衰减系数和频率近似成线性关系,并且组织的黏滞性衰减在总衰减中占有较大比重。随着频率f的增大,衰减系数α也不断增大,信号衰减程度随之加强。实际上,衰减系数与频率近似为线性关系而不是绝对的线性关系。在本文的计算仿真中,n的取值为1.1。
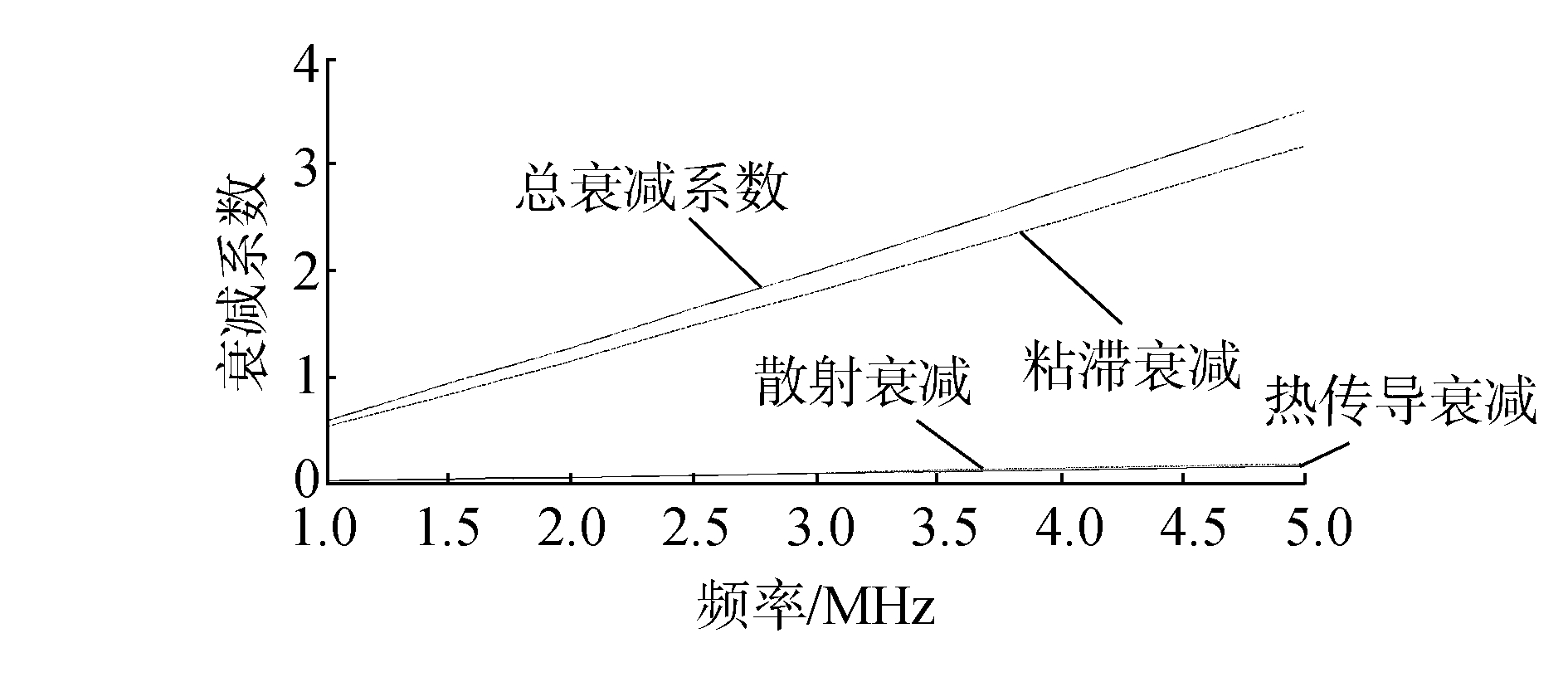
将文献[4]的实验结果与本文计算结果比较,如图 4所示,实验结果与计算结果接近且都随频率呈线性变化,证明了该理论计算公式的可靠性和有效性。该衰减系数计算公式可用于分析超声传播衰减和频率以及生物组织特性的关系,进而应用于超声诊断。

|
Download:
|
| 图 4 计算结果和实验结果比较 | |
生物组织对超声的衰减作用不仅和组织特性以及超声频率有关,与组织厚度也有关系。人体软组织可以看作为线性卷积系统[13],设超声发射信号为x(t),生物组织对超声的衰减作用可以表示为位置和时间的传递响应函数h(r, t):
| $ x\left( t \right) = \left[ {1 - \cos \left( {\frac{{2{\rm{ \mathsf{ π} }}{f_0}t}}{m}} \right)} \right] \cdot \sin \left( {2{\rm{ \mathsf{ π} }}{f_0}t} \right) $ |
| $ h\left( {r,t} \right) = \sum\limits_{i = 1}^N {{A_i}\delta \left( {t - {\tau _i}} \right)} $ |
式中:m表示单音频的个数,f0为信号的中心频率。Ai、τi分别表示组织中不同位置处的信号幅值与时间延迟,Ai=exp(-α(f)cτi)。
超声在组织中传播的频域形式可以简化为
| $ S\left( \omega \right) = X\left( \omega \right)H\left( \omega \right) = X\left( \omega \right) \cdot {{\rm{e}}^{ - \alpha \left( f \right)d}} $ |
生物组织的超声透射特性实验主要使用超声波脉冲发射仪DPR300(由笔记本电脑通过USB串口进行控制),通过日本富士公司的超声波传感器5045S完成超声波的发射和接收,最后通过示波器DO1104获取波形文件及数据。图 5为实验环境。

|
Download:
|
| 图 5 实验环境 | |
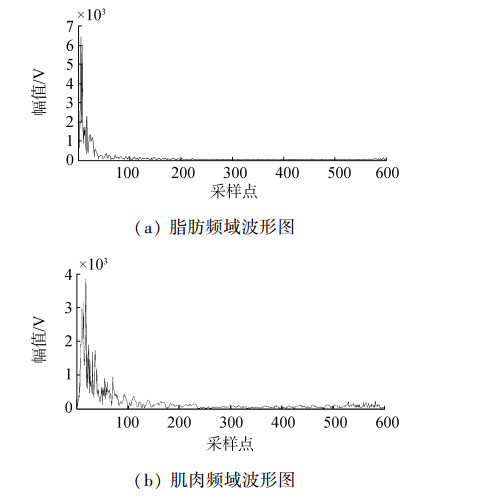
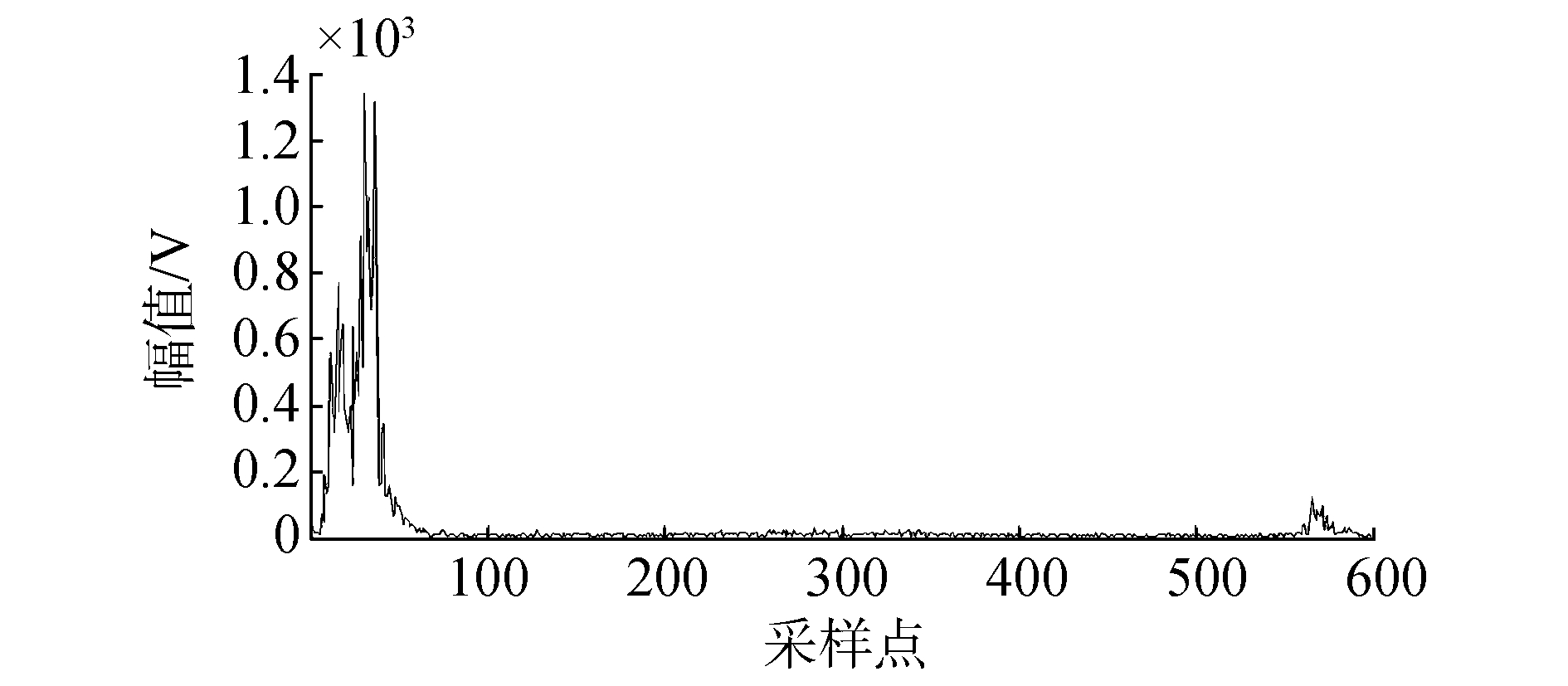
在实验过程中,采用2种样本夹具分别为2.5和5 cm。实验中采用的样本分别为2.5 cm脂肪、2.5 cm肌肉、5 cm脂肪。将不同样本放入在夹具中,通过笔记本控制DPR300发射脉冲,并通过示波器获取测试波形及数据。CVS格式的数据通过MATLAB软件进行谱分析,结果可以见图 6、7。
|
Download:
|
| 图 6 实验谱分析(d=2.5 cm) | |
|
Download:
|
| 图 7 脂肪频域波形图(d=5 cm) | |
通过图 6可见,在组织厚度相同的情况下,脂肪频谱幅值较高,说明超声在肌肉组织中传播时衰减程度较大,这与其组织特性有关系。同时可以看出,超声在肌肉组织中传播时受噪声影响较大,两者的波形发生变化。实验结果与理论计算相吻合,证明了理论分析的准确性,通过谱分析可以较为方便区别肌肉和脂肪组织。
比较2.5和5 cm脂肪组织的谱分析图,两者频谱波形相似,幅值发生了明显变化,且变化规律符合理论计算公式,再次表明了本文计算公式的有效性。基于超声透射法的谱分析对不同组织的可分辨性较高,通过接收波形可以判断组织的厚度以及类别或状态,为超声诊断提供了新的理论依据以及方法。
4 结论1) 本文基于超声波在生物组织中的透射传输机理,对超声波在生物组织中的衰减特性进行了分析,汇总出用于计算分析超声在软组织中传播的衰减公式;
2) 经过计算比较,本文总结的衰减公式可以用于超声对组织的检测分析。生物组织的类型或病理变化往往导致声学特性的变化;
3) 在理论公式的基础上,对生物组织的超声透射信号进行实验的谱分析,结果表明,基于超声透射法的谱分析对组织的可识别性高,可以应用于组织的超声诊断或治疗。这对研究生物组织的生理特性、病理变化都有积极地推动作用。
| [1] |
GONCHARSKY A V, ROMANOV S Y, SERYOZHNIKOV S Y. A computer simulation study of soft tissue characterization using low-frequency ultrasonic tomography[J]. Ultrasonics, 2016, 67: 136-150. DOI:10.1016/j.ultras.2016.01.008 ( 0) 0)
|
| [2] |
MOHAMED M M, SHAAT L T, MAHMOUD A N. Propagation of ultrasonic waves through demineralized cancellous bone[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2003, 50(3): 279-288. DOI:10.1109/TUFFC.2003.1193621 ( 0) 0)
|
| [3] |
吕海涛.生物多层组织的声传输特性研究[D].西安: 陕西师范大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10718-2006116876.htm
( 0) 0)
|
| [4] |
OLIVEIRA D P, SANTOS T Q, MAGGI L E, et al. Ultrasound propagation velocity and acoustic attenuation on agarose phantoms'in three different manufacture techniques[C]//Proceedings of 2014 Pan American Health Care Exchanges. Brasilia, Brazil, 2014: 1-3.
( 0) 0)
|
| [5] |
ABDERRAZEK B, TAREK B. Ultrasonic non-destructive characterization of trabecular bone: Experimental and theoretical prediction of the ultrasonic attenuation[C]//Proceedings of the 20153rd International Conference on Control, Engineering & Information Technology. Tlemcen, Algeria, 2015: 1-6.
( 0) 0)
|
| [6] |
沈祥立.影响医用透射式超声断层成像性能指标的关键技术研究[D].哈尔滨: 哈尔滨工业大学, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D241255
( 0) 0)
|
| [7] |
CUCCARO R, MUSACCHIO C, GIULIANO ALBO P A, et al. Acoustical characterization of polysaccharide polymers tissue-mimicking materials[J]. Ultrasonics, 2015, 56: 210-219. DOI:10.1016/j.ultras.2014.03.018 ( 0) 0)
|
| [8] |
KANAYAMA Y, KAMIYAMA N, MARUYAMA K, et al. Real-time ultrasound attenuation imaging of diffuse fatty liver disease[J]. Ultrasound in medicine & biology, 2013, 39(4): 692-705. ( 0) 0)
|
| [9] |
章东, 郭霞生, 马青玉, 等. 医学超声基础[M]. 北京: 科学出版社, 2014.
( 0) 0)
|
| [10] |
解卓丽, 周浩, 郑音飞. 非均匀组织医学超声发射声场仿真[J]. 声学学报, 2013, 38(6): 657-662. ( 0) 0)
|
| [11] |
LAI Yinan, LUO Jianwei, LIU Xiangdong. Study on interventional ultrasonic thrombus ablation technique[J]. Chinese journal of medical instrumentation, 2002, 26(1): 23-25. ( 0) 0)
|
| [12] |
PÉREZ-LIVA M, HERRAIZ J L, UDÍAS J M, et al. Full-wave attenuation reconstruction in the time domain for ultrasound computed tomography[C]//Proceedings of the 13th International Symposium on Biomedical Imaging. Prague, Czech Republic, 2016: 710-713.
( 0) 0)
|
| [13] |
RAMALLI A, GUIDI F, BONI E, et al. A real-time chirp-coded imaging system with tissue attenuation compensation[J]. Ultrasonics, 2015, 60: 65-75. DOI:10.1016/j.ultras.2015.02.013 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


