2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
船舶在航行过程中,会经历非常复杂的波浪情况及运动,螺旋桨的来流情况会变得非常复杂,浸没深度也会随之发生变化。由于螺旋桨浸没深度的变化,使其与自由液面的关系变得尤为复杂,会出现一些复杂的物理现象,如吸气。当螺旋桨与自由液面十分接近时,螺旋桨的推力和扭矩会由于自由液面的影响而减小,最终导致螺旋桨的效率下降;同时,齿轮和桨轴会发生损伤,船舶的事故率也会不断增加,需要巨额的维修费及停工期。因此,研究自由液面对螺旋桨敞水性征的影响就显得尤为重要。
Kozlowska A M等[1]通过对一系列的吸气试验,对吸气机制进行了研究及分类,通过试验现象的瞬时规律总结出一般规律,并对不同沉深的吸气区域进行了细致的划分。Koushan K等[2]通过在挪威MARINTEK水池进行的试验,研究了沉深、波高及波长对近自由液面的推式推进器的水动力性能的影响,总结出进速系数小于临界进速系数,即J=0.4时,推力会发生急剧下降。Faltinsen[3]、Minsaas[4-5]对吸气情况下波浪对螺旋桨的平均推力及平均转矩的影响进行了分析。Wang Lian-zhou等[6]基于RANS方法,对螺旋桨在近自由液面情况下的旋转及深沉的耦合运动进行模拟,研究了不同时刻的运动状态和不稳定的推力、转矩系数,重点分析了在这种耦合运动中的螺旋桨与自由液面之间的相互关系。郭春雨等[7]通过把MRF与VOF模型相结合的方法,研究了桨轴的深度对螺旋桨推力、扭矩的影响,且模拟结果与试验数据吻合较好,对理解空气吸入的物理本质提供了一种可靠的理论方法。
本文基于RANS方法对螺旋桨在近自由液面的吸气现象进行模拟,对螺旋桨-自由液面的相互作用进行分析,研究不同时刻的吸气对螺旋桨的水动力性能的影响及自由液面的变形情况,并总结不同浸没深度时吸气现象的一般规律,将自由液面的变形、桨叶压力、侧向力及侧向力等联系起来。
1 数学模型 1.1 控制方程不可压缩牛顿流体的运动满足连续性方程和动量守恒方程[8-9]:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0$ | (1) |
| $\begin{gathered} \frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}^\prime {u_j}^\prime ) = \\ - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_i}}}(\mu \frac{{\partial {u_i}}}{{\partial {x_i}}} - \rho \overline {{u_i}^\prime {u_j}^\prime } ) + {S_j} \\ \end{gathered} $ | (2) |
式中:ui和uj是速度分量的时均值(i,j=1,2,3);p是压力的时均值;ρ为流体密度;μ为动力粘性系数;
本文通过VOF方法[10]捕捉自由液面的变形情况。假设计算区域是V,流体1为空气,所在的区域记为V1;流体2为水,所在的区域记为V2。定义函数:
| $\alpha (\vec{x} ,t) = \left\{ {\begin{array}{*{20}{c}} {1,\vec{x} \in {V_1}} \\ {0,\vec{x} \in {V_2}} \end{array}} \right.$ | (3) |
对于由2种不相容的流体组成的流场,
| $\frac{{\partial \alpha }}{{\partial t}} + \vec{U} \cdot {\rm{\nabla}} \alpha = 0$ | (4) |
式中
| ${C_{ijk}} = \frac{1}{{\Delta {v_{ijk}}}}\int_{{I_{ijk}}} {\alpha (\vec{x} ,t)} {\rm{d}}V$ | (5) |
并且
| $\frac{{\partial C}}{{\partial t}} + \vec{U} \cdot \nabla C = 0$ | (6) |
当C=1时,网格充满流体1;当C=0时,网格不含流体1;当0<C<1时,网格包含自由液面。
本文所使用的湍流模型为
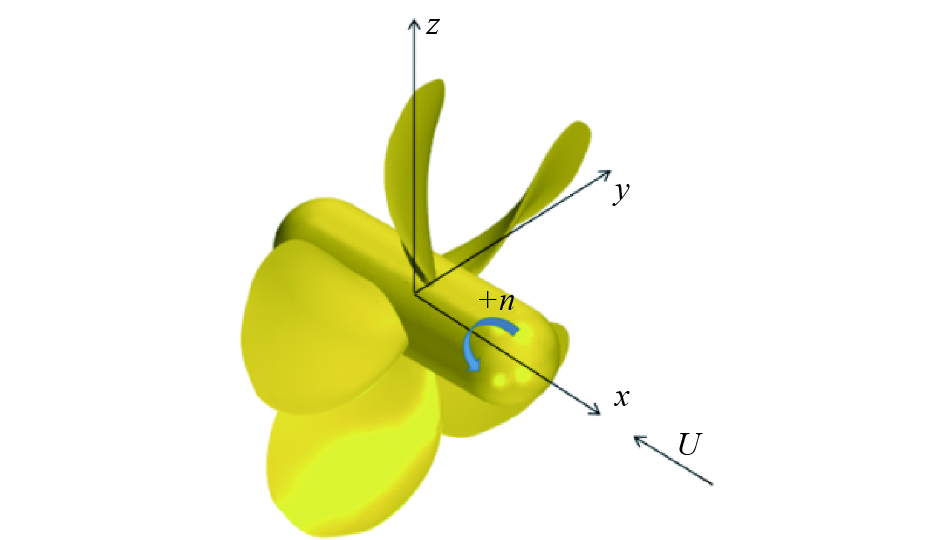
本文以4381型螺旋桨为研究对象,其主要参数如表1所示,螺旋桨的三维几何模型如图1所示。Zhifeng Zhu(2015)[13]基于RANS方法对该系列螺旋桨的空化性能进行了预测和分析。
|
|
表 1 4381螺旋桨主要参数 |
|
Download:
|
| 图 1 4381螺旋桨几何模型 | |
首先对螺旋桨模型进行面网格重构(surface remesher),对螺旋桨表面网格进行处理并生成表面三角化良好的高质量面网格,以面网格为基础生成带有边界层(prism layer mesh)和切割体网格(trimmed mesh)的体网格。剖面z=0的网格分布如图2所示。为了更好地对梢涡、尾涡及自由液面进行捕捉,对其相应位置进行加密;边界层网格应用棱柱形边界层进行捕捉,且层数为20层,y+值取为30,边界层总厚度为4.598×10-3 m,使用滑移网格实现旋转域的旋转。时间步长设置为2.778×10-4 s,对应螺旋桨旋转1°所需要的时间。计算域如图3所示,此次数值模拟的浸没深度分别为h/R=1.2、1.4、1.6及4(敞水)。

|
Download:
|
| 图 2 网格划分形式 | |

|
Download:
|
| 图 3 计算域 | |
进速系数J的取值为0.1~0.9,并每隔0.1进行选取,通过改变来流速度VA(J=VA/nD)的大小来实现进速系数J的变化,同时将螺旋桨转速设定为n=10 r/s的定值,此时,螺旋桨的旋转周期为0.1 s,也就是说,螺旋桨旋转一周的时间为0.1 s;基于螺旋桨的半径R及叶梢的速度U=2nπR,可以定义雷诺数为Re=UR/v=1.28×106,其中,运动粘性系数v=1.14×106 m2/s。推力系数
| ${K_{{T_0}}} = \frac{{{T_0}}}{{\rho {n^2}{D^4}}},\mathop {}\limits_{} {K_{{Q_0}}} = \frac{{{Q_0}}}{{\rho {n^2}{D^5}}},\mathop {}\limits_{} {\eta _0} = \frac{{{K_{T_0}}}}{{{K_{Q_0}}}} \cdot \frac{J}{{2{\rm{\pi }}}}$ | (7) |
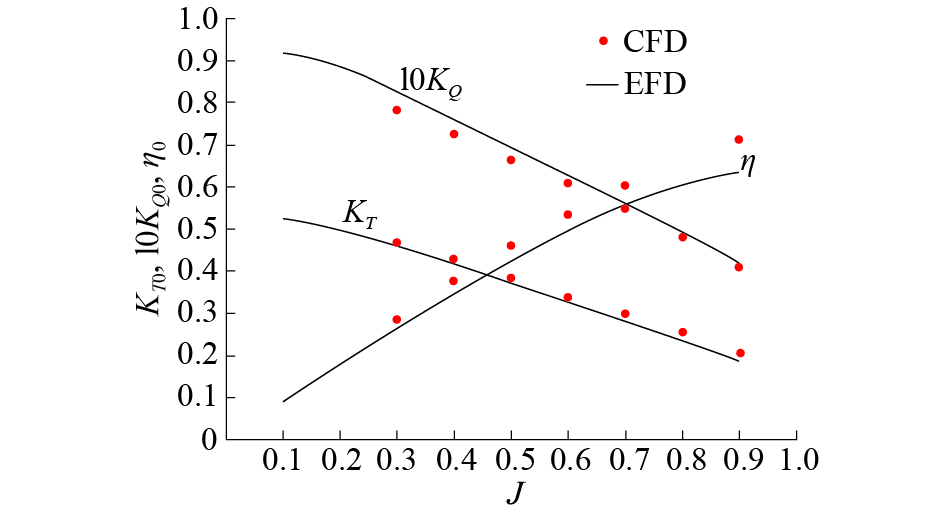
4381螺旋桨的敞水效率曲线如图4所示。从图中可以看出,通过模拟计算得出的敞水状态(h/R=4)时的推力系数
|
Download:
|
| 图 4 4381螺旋桨敞水性征曲线 | |
推力和扭矩的损失系数定义如下:
| ${\beta _T} = \frac{{{K_T}}}{{{K_{{T_0}}}}}$ | (8) |
| ${\beta _Q} = \frac{{{K_Q}}}{{{K_{{Q_0}}}}}$ | (9) |
式中:
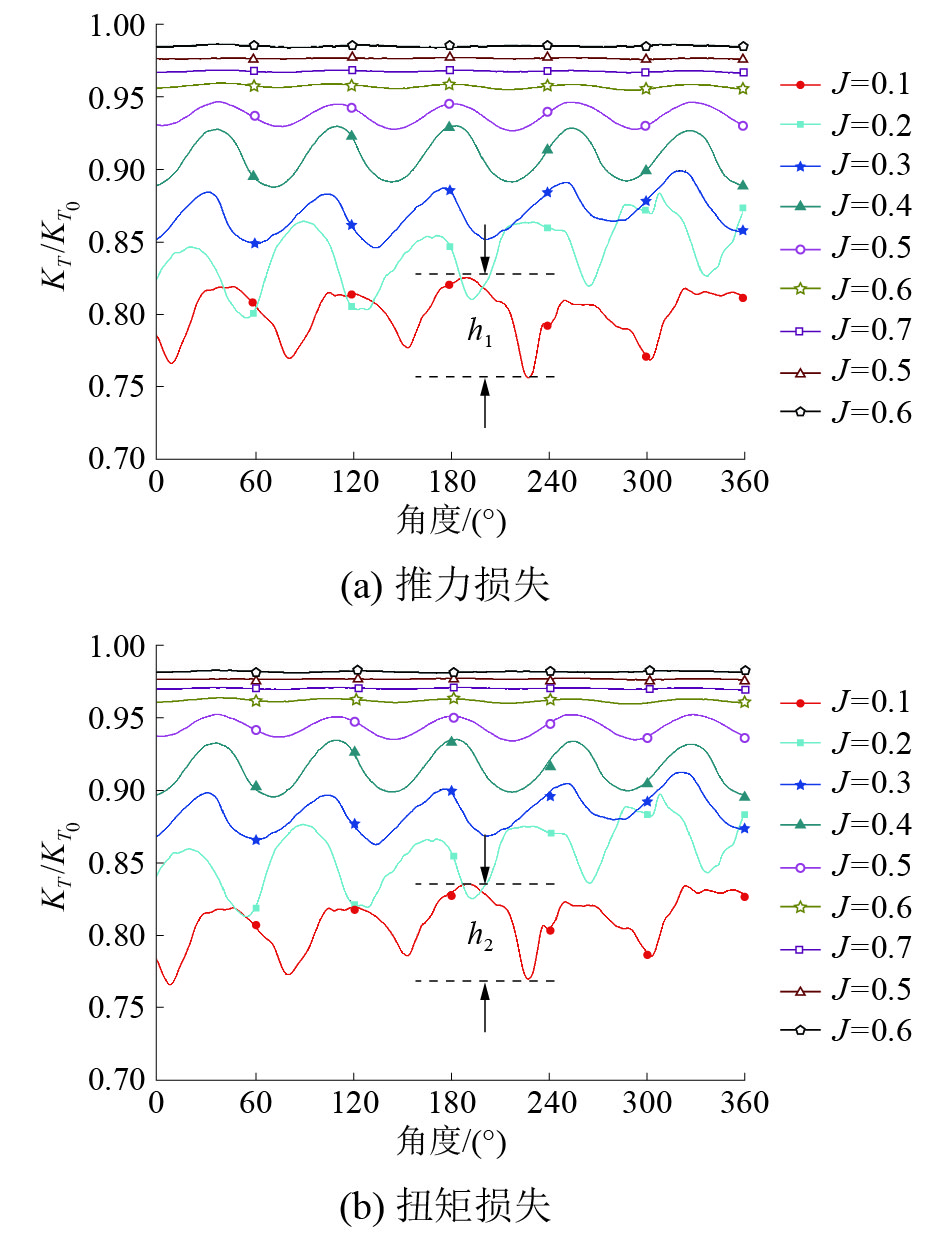
不同进速系数下,螺旋桨的推力及扭矩在一个旋转周期内随旋转角度的变化情况如图5所示。
|
Download:
|
| 图 5 螺旋桨推力及扭矩损失与旋转周期的关系(h/R=1.4) | |
可以发现,不同进速系数下的推力和转矩曲线会发生规则的波动,曲线的波动情况基本一致,并且在一个旋转周期中,波动曲线会经历5次循环。也就是说,波峰及波谷的出现仅仅与螺旋桨的旋转角度有关,与来流速度无关,当螺旋桨旋转23°、97°、173°、245°及319°时,推力和扭矩达到峰值;当螺旋桨旋转57°、125°、201°、276°及351°时,推力和扭矩会达到谷值。进速系数越小,此时自由液面对螺旋桨的影响会变大,推力和转矩的波动会变大,曲线也越加不规律,在图5(a)中,J=0.1时相邻的波峰与波谷的差值h1=0.069,推力的峰值及谷值与均值分别相差3.19%和5.56%;在图5(b)中,J=0.1时相邻的波峰与波谷的差值h2=0.07,转矩的峰值、谷值与均值分别相差3.25%和5.37%。由此,吸气现象会引起螺旋桨的推力及转矩损失并伴有强烈的冲击载荷,导致桨轴、齿轮的方位及螺旋桨发生损坏,对螺旋桨的强度会产生极大的考验;在高进速系数状态下,螺旋桨的推力损失和扭矩损失稳定后,会逐渐接近1,表示几乎没有推力及扭矩的损失。
当螺旋桨的推力和扭矩稳定后,不同浸没深度下的推力损失和扭矩损失的平均值与进速系数的关系如图6所示。可以看出,浸没深度对推力损失与浸没深度对扭矩损失影响的效果相似,当螺旋桨接近自由液面时,推力和扭矩损失的会更多;同时,随着进速系数的增大,推力损失和转矩损失逐渐趋向于1,自由液面对推力和转矩的影响会减小,与上述结论一致。浸没深度h/R=1.2、进速系数J=0.1时,自由液面对螺旋桨的推力及转矩的影响效果最大,分别可达到0.723和0.733。

|
Download:
|
| 图 6 螺旋桨推力损失及扭矩损失曲线 | |
当螺旋桨的推力和扭矩稳定后,h/R=1.4、J=0.1时,螺旋桨的推力损失及单桨叶的推力损失与旋转角度的关系如图7所示。可以看出,单个桨叶会经历更大的波动,最大可达单桨叶推力平均值的70.6%。

|
Download:
|
| 图 7 螺旋桨推力损失及扭矩损失曲线(h/R=1.4) | |
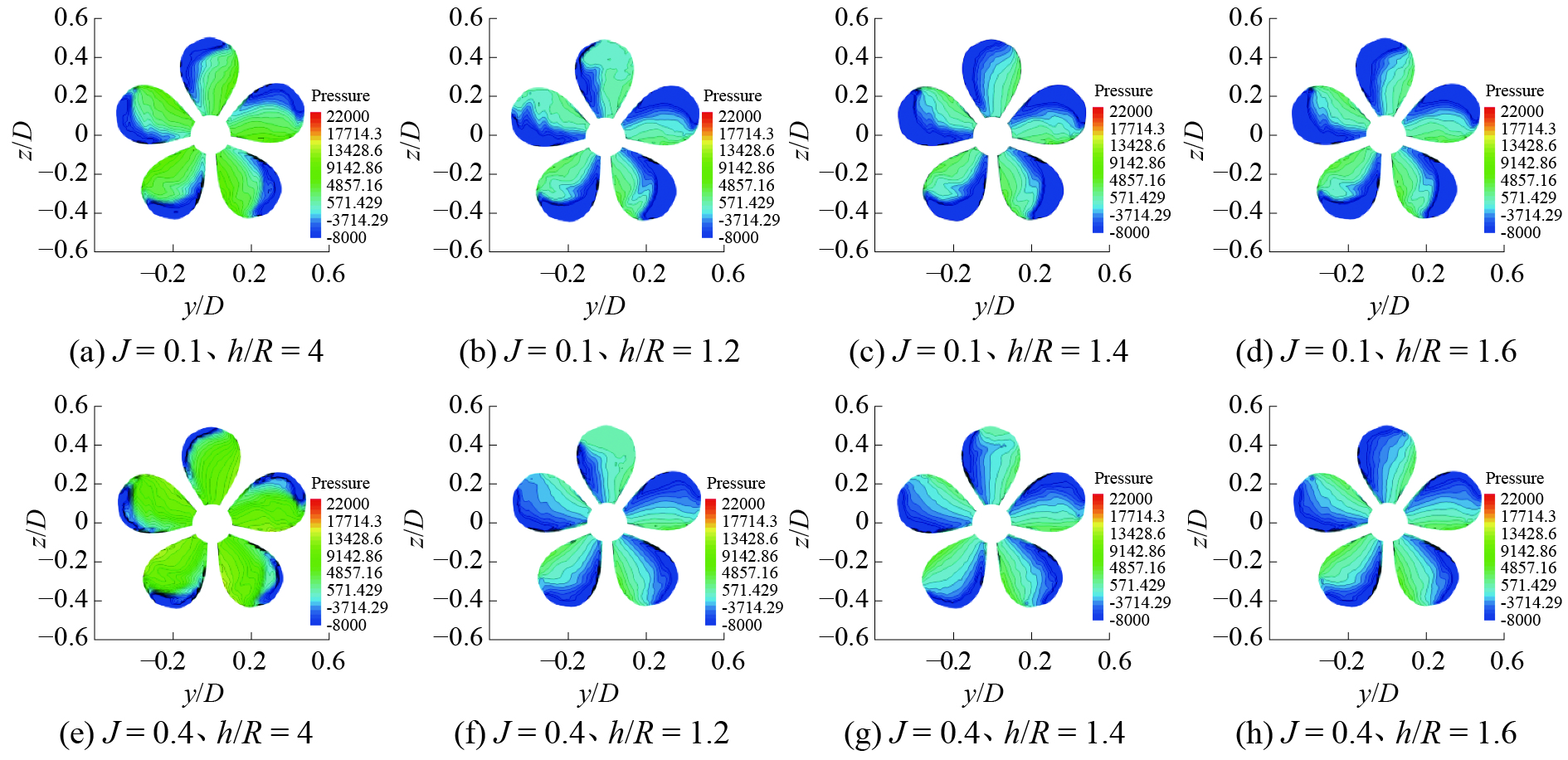
图8、9分别给出了低进速系数状态下的螺旋桨桨叶压力分布图,其中,Y轴和Z轴分别进行无量纲化。可以发现,压力面的压力明显大于吸力面的压力,这是螺旋桨的推力产生的原因。当进速系数J较小时,叶背和叶面的压力差也较大,会产生较大的推力;随着进速系数的增大,叶背和叶面的压力差会减小,螺旋桨的推力也会随着进速系数J的增大相应减小。

|
Download:
|
| 图 8 压力面压力分布 | |
|
Download:
|
| 图 9 吸力面压力分布 | |
螺旋桨在近自由液面工作时,由于与自由液面的相互作用,吸力面和压力面的压力同敞水状态下的相比呈现明显的减小,尤其对于吸力面,吸气导致部分吸力面覆盖空气(如图10),压力减小的更大,因而会导致螺旋桨发生推力损失;同时桨叶的压力分布呈现的不对称性,导致整个螺旋桨的受力分布具有较大的不对称性,螺旋桨除了会产生推力外,也会产生水平侧向力(y方向)和垂向力(z方向),接下来将对水平侧向力和垂向力进行分析。

|
Download:
|
| 图 10 瞬时流场(0.01≤γair≤0.5) | |
螺旋桨在近自由液面工作时,由于螺旋桨−自由液面的相互作用,螺旋桨的受力情况变得十分复杂,此时螺旋桨剧烈的振动,并产生很强的水平侧向力及垂向力,螺旋桨在不同浸没深度的水平侧向力和垂向力与进速系数的关系如图11所示。
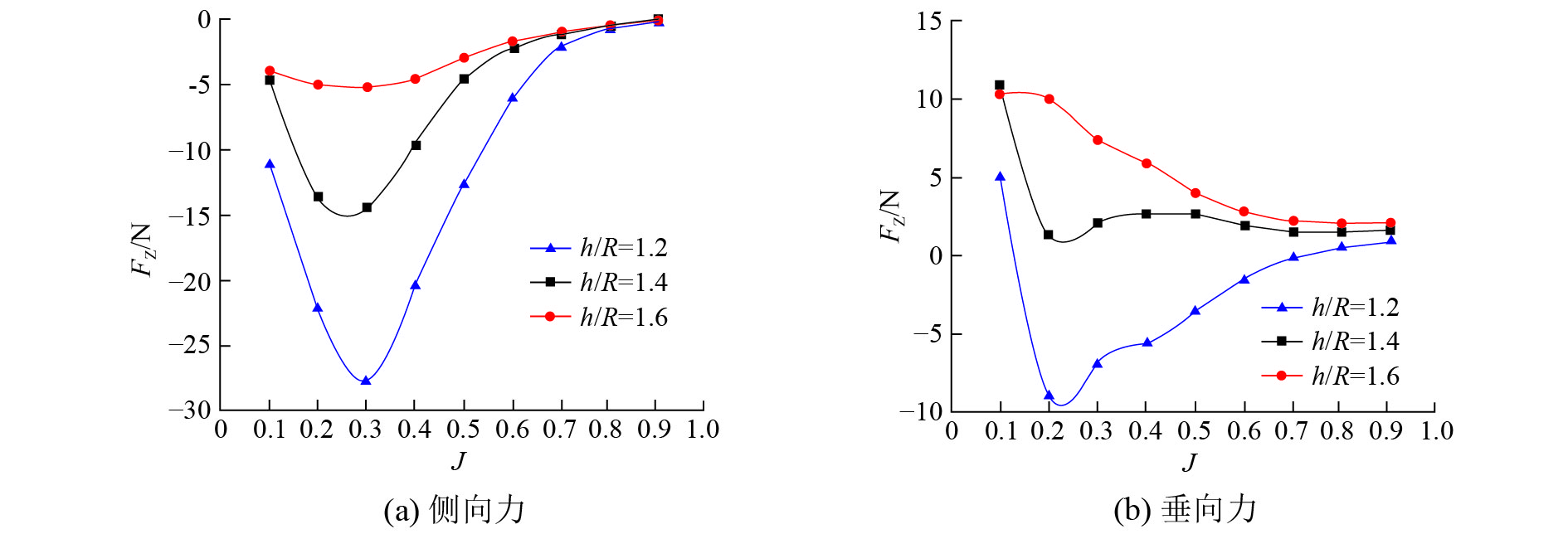
可以发现,螺旋桨产生的水平侧向力与浸没深度呈反比关系,并在进速系数J=0.3时达到峰值,h/R=1.2、1.4、1.6时的最大水平侧向力分别为27.643、14.415和5.191 N;J=0.2、h/R=1.2时,螺旋桨产生的向下的垂向力达到峰值,为8.981 N,h/R=1.4及h/R=1.6产生向上的侧向力,最大分别可达10.797和10.300 N;同时,J=0.9时,不同沉深的水平侧向力和垂向力接近于0,表明此时自由液面对螺旋桨只产生推力。不同浸没深度螺旋桨的水平侧向力及垂向力如表2~4所示。
|
Download:
|
| 图 11 水平侧向力和侧向力与进速系数关系图(光滑) | |
|
|
表 2 侧向力(h/R=1.2) |
|
|
表 3 侧向力(h/R=1.4) |
|
|
表 4 侧向力(h/R=1.6) |
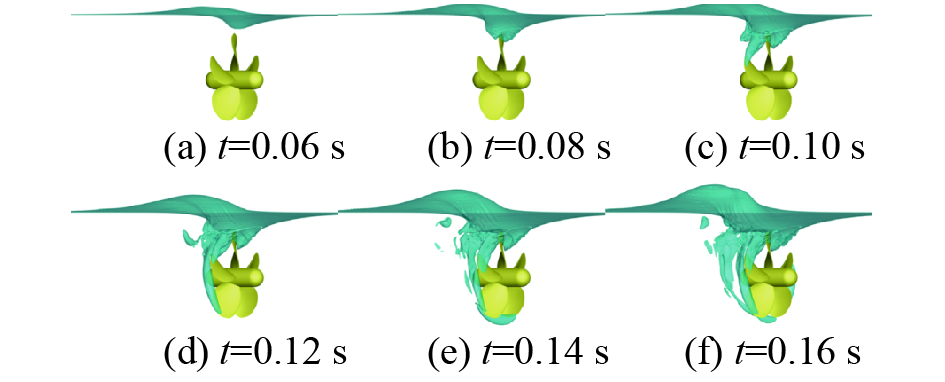
h/R=1.4、J=0.1时,瞬时流场随螺旋桨旋转的变化如图11所示。图12可以显示自由液面的变形过程及吸气的发生过程:包括吸气初始、部分吸气及全吸气状态。可以发现,此时引起吸气现象的主要因素是自由液面涡,由于螺旋桨−自由液面的相互作用,首先螺旋桨上方的自由液面附近形成较小、锥形的“涡”,“涡”继续向下延伸并与桨叶的吸力面接触,夹带的空气也会通过“涡”由自由液面吸入到水中,之后由于梢涡的作用,空气会沿着螺旋桨的旋转方向运动,并逐渐覆盖在螺旋桨的桨叶表面,其中一部分气体会溢出,在t=0.14 s和t=0.16 s时中可以清楚地看到水中残留的气体。
|
Download:
|
| 图 12 瞬时流场(h/R=1.4、J=0.1) | |
t=0.22 s时,空气体积分数在0 ~ 0.5的瞬时流场如图10所示,此时螺旋桨处于全吸气状态,螺旋桨的正上方直接与空气接触,并且螺旋桨的吸力面大部分会被残留在水中的空气所覆盖,螺旋桨工作的周围环境被气泡覆盖,对螺旋桨的水动力性能会产生严重影响。
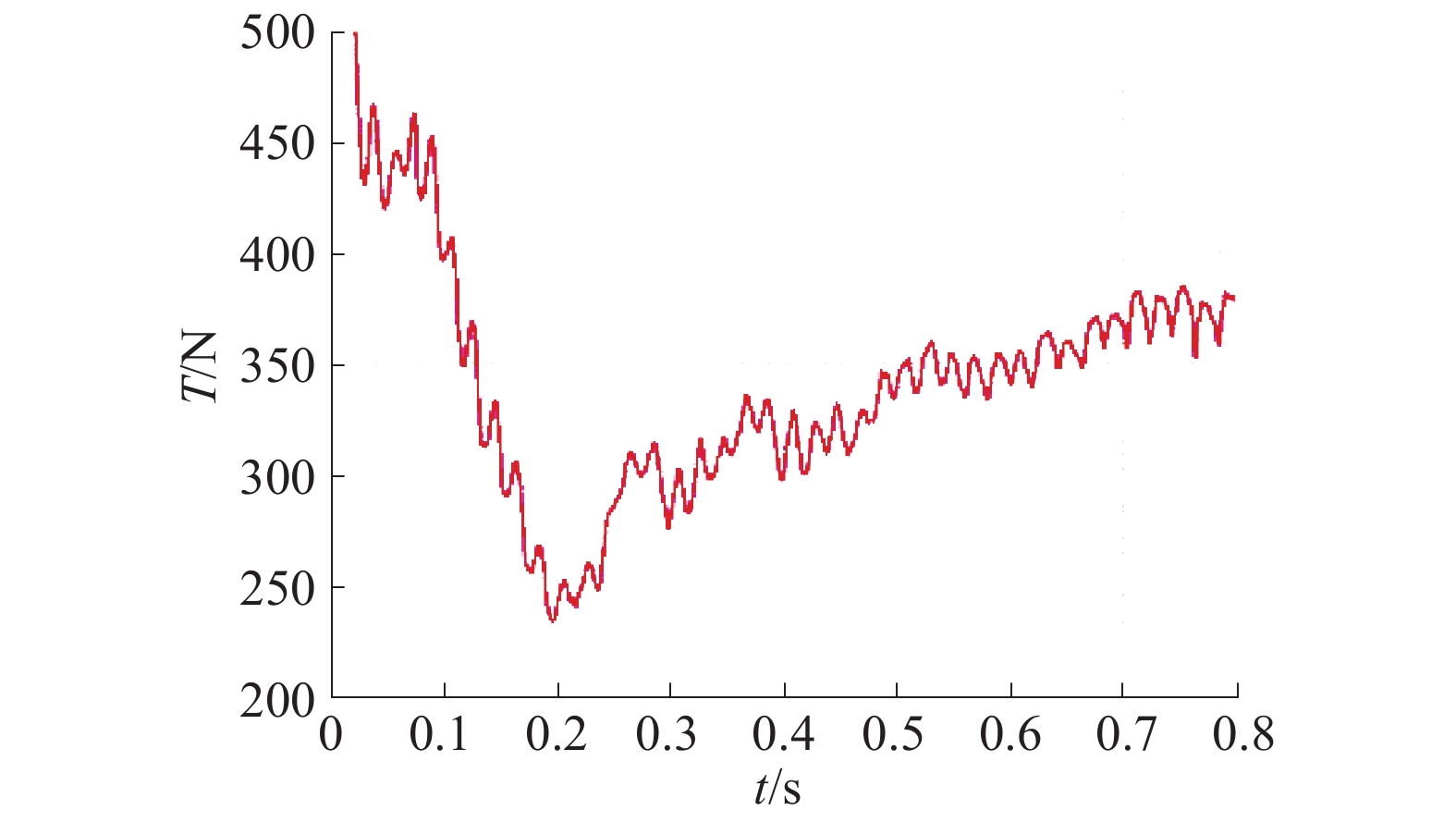
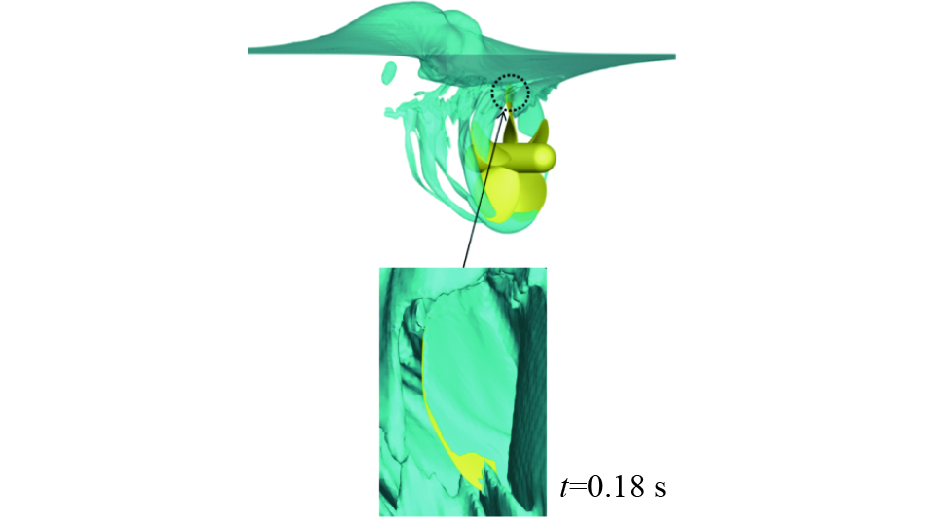
h/R=1.4、J=0.1时,螺旋桨的推力曲线如图13所示。最开始推力相对平稳没有可见的吸气现象。随后,吸气的发生使得空气穿透自由液面并覆盖在桨叶表面,尤其在吸力面,导致压力的突然增加,从而螺旋桨经历突然的推力损失,吸气现象会突然发生,推力及扭矩会有快速而剧烈的波动,螺旋桨会经历推力及扭矩的突然损失推力迅速减小。当t=0.18 s(如图14所示),螺旋桨处于全吸气状态,大部分桨叶被气泡覆盖,并且螺旋桨的桨叶会与空气相接触,叶片会做液面划割运动,桨叶会经历交替的入水、出水,桨叶的随边也会受到很大的冲击压力,导致更严重的推力损失和转矩损失,此时,推力曲线达到最低点,螺旋桨产生的最小推力为233.299 N,与推力稳定后的均值相比推力损失为0.501。此外,一个桨叶在一个旋转周期所受推力大小变化很大,会引起强烈的冲击载荷,导致桨轴、齿轮的方位及螺旋桨发生损坏这样就会对桨叶造成疲劳破坏。
|
Download:
|
| 图 13 螺旋桨的推力曲线(h/R=1.4、J=0.1) | |
|
Download:
|
| 图 14 自由液面变化(h/R=1.4、J=0.1) | |
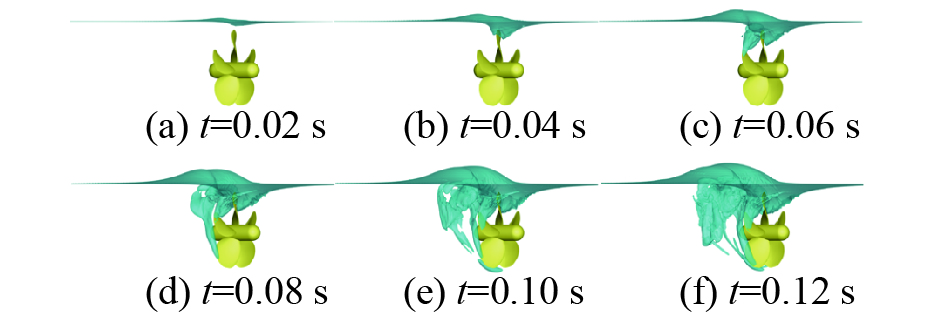
h/R=1.2、J=0.1时的瞬时流场随螺旋桨旋转的变化如图15所示,吸气过程与图12相似,对于小浸没深度来说,自由液面涡的形成时间较短;h/R=1.2时,梢涡在吸气中会发挥更为重要的作用,吸气现象发生的时间更短、对自由液面的扰动更为强烈。
|
Download:
|
| 图 15 瞬时流场(h/R=1.2,J=0.1) | |
本文对在不同进速系数和浸没深度下的五叶螺旋桨4381在近自由液面时的运动进行数值模拟,详细分析了螺旋桨与自由液面的相互作用关系,并通过对不同时刻螺旋桨的受力情况及吸气现象的分析,研究了吸气的发生过程。并且通过VOF方法较好地捕捉了自由液面的变形情况,以及气腔、浪花及波浪的出现。可以发现:
1)进速系数和浸没深度是造成螺旋桨吸气的主要原因,自由液面涡和梢涡是影响吸气现象的主要因素,吸气的初始阶段中,自由液面涡使得空气向下吸入;之后,叶梢与空气相接触,此时梢涡在吸气中发挥着重要作用。
2)螺旋桨在近自由液面工作时,会造成螺旋桨的推力损失和转矩损失,进速系数和浸没深度越小,推力损失和转矩损失的变化波动越剧烈,稳定后的平均值也越小;同时,桨叶压力的不对称分布会使螺旋桨产生水平侧向力和垂向力;螺旋桨的运动会使自由液面发生变形,变形情况会随着进速系数、浸没深度和时间的变化而变化,进而对螺旋桨的受力情况等产生影响;螺旋桨的浸没深度越小,吸气现象发生的时间越短、自由液面的变形情况越复杂,此时,梢涡对吸气的作用增大。
3)当螺旋桨足够接近自由液面时,桨叶会经历交替的入水、出水,叶片会做液面划割运动,桨叶的随边也会受到很大的冲击压力,导致更严重的推力损失和转矩损失,并对螺旋桨的性能和强度提出了更高的要求。
| [1] |
KOZLOWSKA A M, STEEN S, KOUSHAN K. Classification of different type of propeller ventilation and ventilation inception mechanism[J]. Anthropology news, 2014, 47(9): 56-57. ( 0) 0)
|
| [2] |
DAVID S, SEFIANE K, TADRIST L. Experimental investigation of the effect of the ambient gas on evaporating sessile drops[J]. Defect and diffusion Foru, 2009: 461-468. ( 0) 0)
|
| [3] |
FALTINSEN O M, MINSAAS K J, LIAPIS N, et al. Prediction of resistance and propulsion of a ship in a seaway[C]//Proceedings of 13th Symposium on Naval Hydrodynamics. Tokyo, Japan, 1981: 505-529.
( 0) 0)
|
| [4] |
MINSAAS K J, FALTINSEN O M, PERSSON B.. On the importance of added resistance, propeller immersion and propeller ventilation for large ships in a seaway[C]//Proceedings of International Symposium on Practical Design of Ships and other Floating Structures. Tokyo, Japan, 1983.
( 0) 0)
|
| [5] |
MINSAAS K J, THON H J, KAUCZYNSKI W, et al. Estimation of required capacity for operation of offshore vessels under severe weather conditions[C]//Proceedings of International Symposium on Practical Design of Ships and Other Floating Structures. Trondheim, Norway, 1987.
( 0) 0)
|
| [6] |
W Lianzhou, G Chunyu, W Lei, et al. Numerical analysis of propeller during heave motion near a free surface[J]. Marine technology society journal, 2017, 51(1): 40-51. DOI:10.4031/MTSJ.51.1.5 ( 0) 0)
|
| [7] |
GUO C Y, ZHAO D G, SUN Y. Numerical simulation and experimental research on hydrodynamic performance of propeller with varying shaft depths[J]. China ocean eng, 28(2): 271-282. DOI:10.1007/s13344-014-0022-7 ( 0) 0)
|
| [8] |
H Shiba. Air-drawing of marine propellers[R]. Transportation Technical Research Institute, Tokyo : Unyu Gijutsu Kenkyujo, 1953.
( 0) 0)
|
| [9] |
PENG H, QIU W, NI S. Effect of turbulence models on RANS computation of propeller vortex flow[J]. Ocean engineering, 2013, 72(4): 304-317. ( 0) 0)
|
| [10] |
HIRT C W, NICHOLS B D. Volume of fluid(VOF)method for the dynamics of free boundary[J]. Compute phys, 1981, 39: 201-225. DOI:10.1016/0021-9991(81)90145-5 ( 0) 0)
|
| [11] |
SHIH T H, LIOU W W, SHABBIR A, et al. A new k-ω eddy-viscosity model for high Reynolds number turbulent flows-model development and validation
[J]. Computers fluids, 1995, 24(3): 227-238. DOI:10.1016/0045-7930(94)00032-T ( 0) 0)
|
| [12] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 ( 0) 0)
|
| [13] |
ZHU Z. Numerical study on characteristic correlation between cavitating flow and skew of ship propellers[J]. Ocean engineering, 2015, 99: 63-71. ( 0) 0)
|
| [14] |
WANG L Z, GUO C Y, SU Y M, et al. A numerical study on the correlation between the evolution of propeller trailing vortex wake and skew of propellers[J]. International journal of naval architecture and ocean engineering, 2018, 10(2): 212-224. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


