由于水下成像环境的特殊性，噪声干扰，以及机器人其他子系统对光学系统的影响，使得水下图像的质量往往较差，具有对比度低、效果差、细节模糊、灰白效应等特点。直接在这样的图像上进行管道检测将会影响到检测结果，因此需要先对采集到的水下图像进行预处理。本文对水下管道图像进行预处理的主要目的是消除图像中的噪声干扰，增强管道的边缘信息，削弱图像中的无关信息，并且最大限度地简化图像数据，从而改进后续管道检测的可靠性。

1 水下图像的特点

由于水体结构的特殊性，水对光的吸收和散射作用，导致水下成像的效果要远远差于空气中的成像效果^[1]。总结水下成像的特点，主要表现为以下几点：

1) 灰白效应。对于彩色图来说，因为水分子对光的吸收具有选择性，光谱中的红紫色光衰减速度大于蓝绿色光的衰减速度，随着成像深度的增加，衰减速度快的红紫色光将逐渐从图像中消失，图像明显呈蓝绿色，导致图像色彩丢失或者失真。

2) 对比度低。由于水下光源不足，水分子以及水中微粒对光的散射作用，使得水下图像往往具有亮度不均、细节模糊、对比度差、图像质量退化等特点，加大了从图像中提取有用的目标物信息的难度。

3) 清晰度差别较大。因为水对光的吸收严重，为了提高成像的距离，水下成像时往往会加上辅助光源，但这样做一方面加大了水对光的散射作用；另一方面也会带来聚光效应，即成像的亮度会以辅助光源的最强点为中心，沿径向逐渐减弱，导致背景的灰度分布不均^[1]。

为了从水下图像中获取目标的信息，应该针对水下图像的特点，从图像去噪和图像增强两个方面设计出有效的算法，强化目标的特征，弱化背景信息，为后续的目标检测奠定基础。

2 图像降采样

考虑到对于一幅水下管道图像，除了管道以外，其他一些小的几何结构、边缘、微小的细节信息等并不是我们感兴趣的。因此，在滤波阶段对水下管道图像进行适当的模糊，平滑掉图像背景中一些细小的直线边缘，可以减少对后续直线检测过程的干扰^[2]。高斯滤波具有平滑图像的效果，所以本文选用高斯滤波来进行水下管道图像的滤波处理。

2.1 高斯降采样

高斯降采样的步骤为：首先将原图像与高斯核函数进行卷积运算，然后再进行下采样^[3]。卷积运算的表达形式为^[4]

$u(x,t) = {u_0}(x)*G(x,t) \;\;\; x \in {R^n}, \;\;\; t \in (0,\infty )$

式中高斯核函数

$G\left( {x,t} \right) = {(2\pi t)^{ - N/2}}\exp \left( { - {{\left| x \right|}^2}/2t} \right)$

式中 $N$ 是维度。进行卷积运算之后，图像中像素点的灰度值用邻域内像素点的加权值来代替，并且权值的大小是随着该点与中心点的距离单调递减的^[5]，参数 $t$ 的大小决定邻域的大小， $t$ 越大，图像的平滑效果就越好。同时，二维的高斯核函数具有旋转对称性,即高斯滤波对图像的平滑程度在各个方向上是一致的。高斯平滑滤波能有效去除图像中的高斯噪声，具有平滑图像的效果。

对于一幅大小为704×576的水下管道图像，采用高斯平滑滤波之后，对图像进行隔行隔列降采样，可获得大小为352×288的图像。这样每处理一次，得到的新的图像宽与高是原来图像的1/2。对水下管道图像进行2次高斯降采样处理，得到宽高为原图像的1/2大小的新图像，后续处理都是在缩小尺度之后的图像上进行处理，大大缩小了算法的计算量，加快了处理速度。图1显示了采用高斯降采样的方法对水下管道图像进行处理的结果。

从图1的处理结果可以看出，经过高斯降采样，图像中的噪声得到了有效地去除，但是管道的边缘也在滤波过程中被模糊了，这是我们不希望得到的结果。考虑到高斯平滑滤波过程中对各个方向的平滑程度都是一样的，不会偏向边缘一方，因此存在模糊边缘的缺陷。为了解决这一问题，这里引入图像尺度空间的方法，并结合非线性尺度空间能在模糊图像时保护边缘的优点，对高斯降采样进行了改进。

2.2 图像的尺度空间 2.2.1 线性尺度空间

尺度空间的思想就是来源于热传导方程，最早提出于1962年，但是并没有得到重视。直到非线性扩散方程、形态学等方法在计算机视觉领域得到了的广泛应用，图像尺度空间的方法才逐渐发展起来^[6]。

对于一幅灰度值分布不均的图片，就好比区域 $\varOmega $ 内各点的温度不同，随着时间的推移，相邻点之间进行热量传递，最终的结果是各点的温度相同。同理，图像中一点的灰度值如果比周围点的高，则降低其灰度值，反之，则提高其灰度值，实质上就是图像平滑的过程^[7]。图像的线性扩散方程为

$\left\{ {\begin{aligned}& {\frac{{\partial I}}{{\partial t}} = {\rm{div}}(\nabla I) = \Delta I(x,y)} \\ & {I(x,y,0) = {I_0}(x,y)} \end{aligned}} \right.$

高斯滤波的核心思想是将图像与高斯核函数进行卷积运算，即 $u\left( {x,t} \right) = {u_0}\left( x \right)*G\left( {x,t} \right)$ ，其中高斯核函数 $G\left( {x,t} \right) = {(2\pi t)^{ - N/2}}\exp ( - |x{|^2}/2t)$ ，可以证明u(x, t)就是线性扩散方程的解。

线性尺度空间存在以下缺点：光滑图像时，图像中所有点的灰度值在各方向上的扩散是相同的，这就会导致图像平滑的同时，边缘也会被模糊了。为了克服这一缺点，Perona和Malik对线性尺度空间进行了改进，提出了各向异性的扩散方程模型。

2.2.2 非线性尺度空间

在线性尺度空间中，各个点处的传导系数是一样的，导致图像去噪的过程中边缘也被平滑了。为了保护边缘信息，则希望在图像中存在边缘的地方，扩散系数可以自动地降低，这样可以保护边缘不受到影响。Perona和Malik在对线性尺度空间进行改进的基础上，提出了图像的非线性尺度空间模型，也称为各向异性扩散模型，表达式如下：

$\left\{ {\begin{aligned} & {\frac{{\partial I}}{{\partial t}} = {\rm{div}}[g(\left| {\nabla {I_t}} \right|)\nabla {I_t}]} \\ & {I(x,y,0) = {I_0}(x,y)} \end{aligned}} \right.$

式中：div表示散度；I_t为 $t$ 时刻的图像； $g(|\nabla {I_t}|)$ 为扩散函数，表示该点出的扩散强度，它是关于梯度幅值 $|\nabla {I_t}|$ 的光滑单调递减函数，常用的2种表达形式为

$g(\left| {\nabla {I_t}} \right|) = \frac{1}{{1 + {{(\displaystyle\frac{{\left| {\nabla {I_t}} \right|}}{k})}^2}}}$

和

$g(\left| {\nabla {I_t}} \right|) = {{\rm e}^{ - {{(\frac{{\left| {\nabla {u_t}} \right|}}{k})}^2}}}$

P-M模型的基本思想是：当 $|\nabla {I_t}|$ 较大时，表明当前像素点处存在边缘，则扩散函数值较小，平滑程度较低；反之， $|\nabla {I_t}|$ 越小的区域平滑程度越大。这样，随着时间的推进(即迭代次数的增多)，图像会越来越平滑，一些小尺度的几何结构会消失，只保留一些大尺度的边缘信息。

2.3 改进的图像降采样方法

根据上文的分析，本文利用非线性尺度空间的思路，构造了一种新的图像降采样方法。

水下图像是二维离散的数字化图像，因此采用有限差分法对式中的梯度和散度运算进行离散，可以获得P-M模型的四邻域的数值表达形式

$\begin{aligned}{I^{n + 1}}(x,y) = & {I^n}(x,y) + \Delta t\{ {\rm{g(}}\left| {\nabla _N^n(x,y)} \right|{\rm{)}}\nabla _N^n(x,y) + \\& g(\left| {\nabla _S^n(x,y)} \right|)\nabla _S^n(x,y) + g(\left| {\nabla _E^n(x,y)} \right|)\nabla _E^n(x,y) + \\& g(\left| {\nabla _W^n(x,y)} \right|)\nabla _W^n(x,y)\} \end{aligned}$

式中 ${I^n}(x,y)$ 表示第 $n$ 次迭代之后的图像，下标N、S、E、W分别为north、south、east、west的缩写，梯度差分表达式如下：

$\left\{ {\begin{aligned}& {\nabla _{\rm{N}}^n(x,y) = {I^n}(x,y - 1) - {I^n}(x,y)} \\ & {\nabla _{\rm{S}}^n(x,y) = {I^n}(x,y + 1) - {I^n}(x,y)} \\ & {\nabla _{\rm{E}}^n(x,y) = {I^n}(x - 1,y) - {I^n}(x,y)} \\ & {\nabla _{\rm{W}}^n(x,y) = {I^n}(x + 1,y) - {I^n}(x,y)} \end{aligned}} \right.$

如果迭代次数太多，虽然可以平滑背景，减少其对线段检测的干扰，但是算法所耗费的时间太长，不符合系统对于算法的实时性要求。同时，在P-M模型中，当梯度值很大时，扩散函数 $g(|\nabla {I_t}|)$ 的值趋近于0，但是始终不为0，也就是说P-M非线性模型对于边缘仍然存在模糊作用，因此迭代次数不宜过多。另一方面，在保留图像主体信息(即管道)的基础上对图像的尺寸进行缩小可以减少图像的数据量，提高后续图像处理算法的速度。

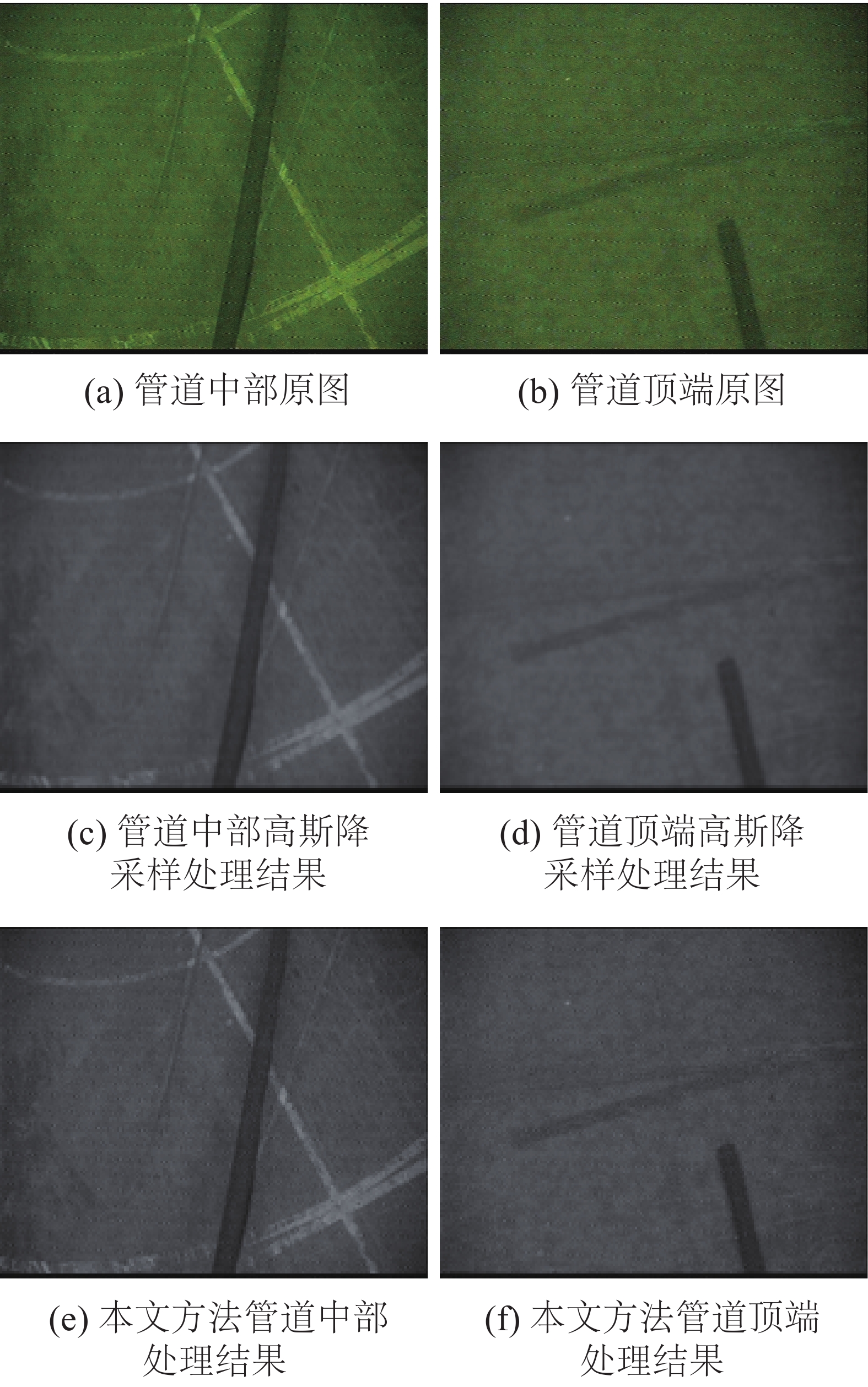
综合以上分析，本文将非线性尺度空间和图像降采样结合起来，在每次迭代时对图像进行隔行隔列降采样，即只需要隔行隔列地计算迭代之后的图像，这样可以使迭代的过程的计算量减少一半。本文对水下管道图像进行2次迭代，获得大小为原图尺寸1/4的图像。图2显示了分别用高斯降采样和本文方法对水下管道图像进行降采样的结果(为了更清楚地显示降采样之后的图像，这里将降采样后的图片显示为与原图同样的大小)。

由图2可以看出，本文的方法能有效去除水下管道图像中的噪声。与高斯降采样方法相比，本文算法能够较好地保留管道的边缘信息。

3 图像增强

水下图像除了有噪声干扰之外，还存在管道与背景的对比度低、灰白效应等缺点。因此需要进行图像增强处理，以保证后续直线检测算法的顺利进行。图像增强的目的是选择性地突出图像中的目标物区域，弱化干扰和背景区域，提高图像的可读性。图像增强算法可分为两大类：空间域的图像增强算法和频域的图像增强算法^[8]。空间域的算法大多数是基于像素点灰度值的映射变换，比较直观简便，传统的算法有直方图均衡化、灰度的线性(非线性)变换等。而频域的方法则比较复杂且计算量大，本文将不作论述。1965年模糊理论诞生，之后Pal和King首次将模糊理论与图像处理结合起来，提出了图像的模糊增强算法，且增强效果比传统的增强算法的效果要好^[9]。本节详细分析了Pal和King提出的传统的模糊增强算法，结合水下管道图像的特点，对传统的模糊增强算法作出改进，并进行了试验验证和对比分析^[10]。

3.1 传统的模糊增强算法

在Pal和King提出的经典模糊增强算法中，将一幅大小为 $M \times N$ 的图像 $ X$ 表示为一个模糊矩阵：

$ X = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{\mu _{11}}}}{{{x_{11}}}}}&{\displaystyle\frac{{{\mu _{12}}}}{{{x_{12}}}}}& \cdots &{\displaystyle\frac{{{\mu _{1N}}}}{{{x_{1N}}}}} \\[8pt] {\displaystyle\frac{{{\mu _{21}}}}{{{x_{21}}}}}&{\displaystyle\frac{{{\mu _{22}}}}{{{x_{22}}}}}& \cdots &{\displaystyle\frac{{{\mu _{2N}}}}{{{x_{2N}}}}} \\[5pt] \vdots & \cdots & \cdots & \vdots \\[5pt] {\displaystyle\frac{{{\mu _{M1}}}}{{{x_{M1}}}}}&{\displaystyle\frac{{{\mu _{M2}}}}{{{x_{M2}}}}}& \cdots &{\displaystyle\frac{{{\mu _{MN}}}}{{{x_{MN}}}}} \end{array}} \right]$

式中的元素μ_ij/x_ij表示坐标在(i, j)处的像素点灰度值x_ij相对于某个特定灰度值x_k的隶属度μ_ij(取值范围为0～1)，经典的隶属度函数的表达形式为

${\mu _{ij}} = T({x_{ij}}) = {[1 + \frac{{(L - 1) - {x_{ij}}}}{{{F_d}}}]^{ - {F_e}}}$

式中：F_e通常取2， $L = 256$ ，F_d的值由渡越点X_c的值来确定，渡越点的意义是当x_ij=x_c时，隶属度的值为0.5。根据x_c可以获得：

${F_d} = \frac{{(L - 1) - {X_c}}}{{{2^{\frac{1}{{{F_e}}}}} - 1}}$

将图像转换到模糊域后，对隶属度值进行如下非线性变换：

${u_{ij}}^\prime = I({\mu _{ij}}) = \left\{ {\begin{array}{*{20}{c}}{2{{({\mu _{ij}})}^2}\;\;\;\;\;\;\;\;\;\;\;\;0 \leqslant {\mu _{ij}} \leqslant 0.5}\\{1 - 2{{(1 - {\mu _{ij}})}^2}\;\;\;\;\;0.5 < {\mu _{ij}} \leqslant 1}\end{array}} \right.$

然后对变换后的隶属度值 ${u_{ij}}^\prime $ 进行逆运算，可获得变换后的灰度值：

${x_{ij}}^\prime = {T^{ - 1}}({\mu _{ij}}^\prime )$

分析可知，经典模糊增强算法的思路是：将图像通过隶属度函数变换到模糊域下，在模糊域进行非线性变换，最后逆变换到空间域中^[11]。实现的效果是在空间域内，以渡越点为界，对左右的灰度值进行拉伸，小于x_c的灰度值减小，大于x_c的灰度值增大，最终达到了提高对比度(目标与背景之间)的目的^[12]。

但是这种方法将逆变换之后小于0的 ${x_{ij}}^\prime $ 值硬性地设为0，这样会损失原图中低灰度的信息，且算法需要经过在空间域和模糊域之间进行2次变换，计算量较大。本文在经典模糊增强算法的基础上，作出一些改进，设计了一种根据灰度直方图的信息确定渡越点值的增强算法^[13]。

3.2 改进的模糊增强算法

模糊增强算法实现的效果是对灰度值进行非线性的拉伸，拉伸的效果可用图3中的曲线近似地描述。

如果我们直接对像素的灰度值做类似的非线性变换，也可以达到拉伸灰度值、提高图像对比度的效果，还可以避免求模糊集和逆运算的步骤，节省大量的时间。为此，本文对模糊增强算法做出了如下改动：

${x_{ij}}^\prime = \left\{ {\begin{array}{*{20}{c}}{x_{ij}^2/{x_c}}\\{L - {{(x - L)}^2}/(L - {x_c})}\end{array}\;\;\;\;\;} \right.\begin{array}{*{20}{c}}{0 \leqslant {x_{ij}} < {x_c}}\\{{x_c} \leqslant {x_{ij}} \leqslant L}\end{array}$

(1)

式中：x_c为渡越点， $L = 255$ ，式(1)中不存在灰度级的损失。而关于渡越点x_c的值的选取，本文采用一种简单的基于直方图统计的方法。首先统计图像中灰度值为x(0~255)的像素点的个数n_x，然后找出拥有最多像素点个数的灰度值x_max。我们认为水下管道图像中背景是占大部分的，管道只占一小部分，x_max可以大概地反映出图像背景的灰度范围。因此，为了提高背景和目标物(管道)之间的对比度，们取x_c=x_max±f，本文中f的值取为10。

为了加快算法速度，先求出所有灰度值(0～255)经式(1)的映射结果，并保存到一个索引表中。对于每个像素点，增强后的灰度值 ${x_{ij}}^\prime $ 可以根据原始灰度值x_ij直接到索引表中去查找，这样避免了重复运算的耗时，大大提高算法的速度。

4 图像增强结果及对比分析

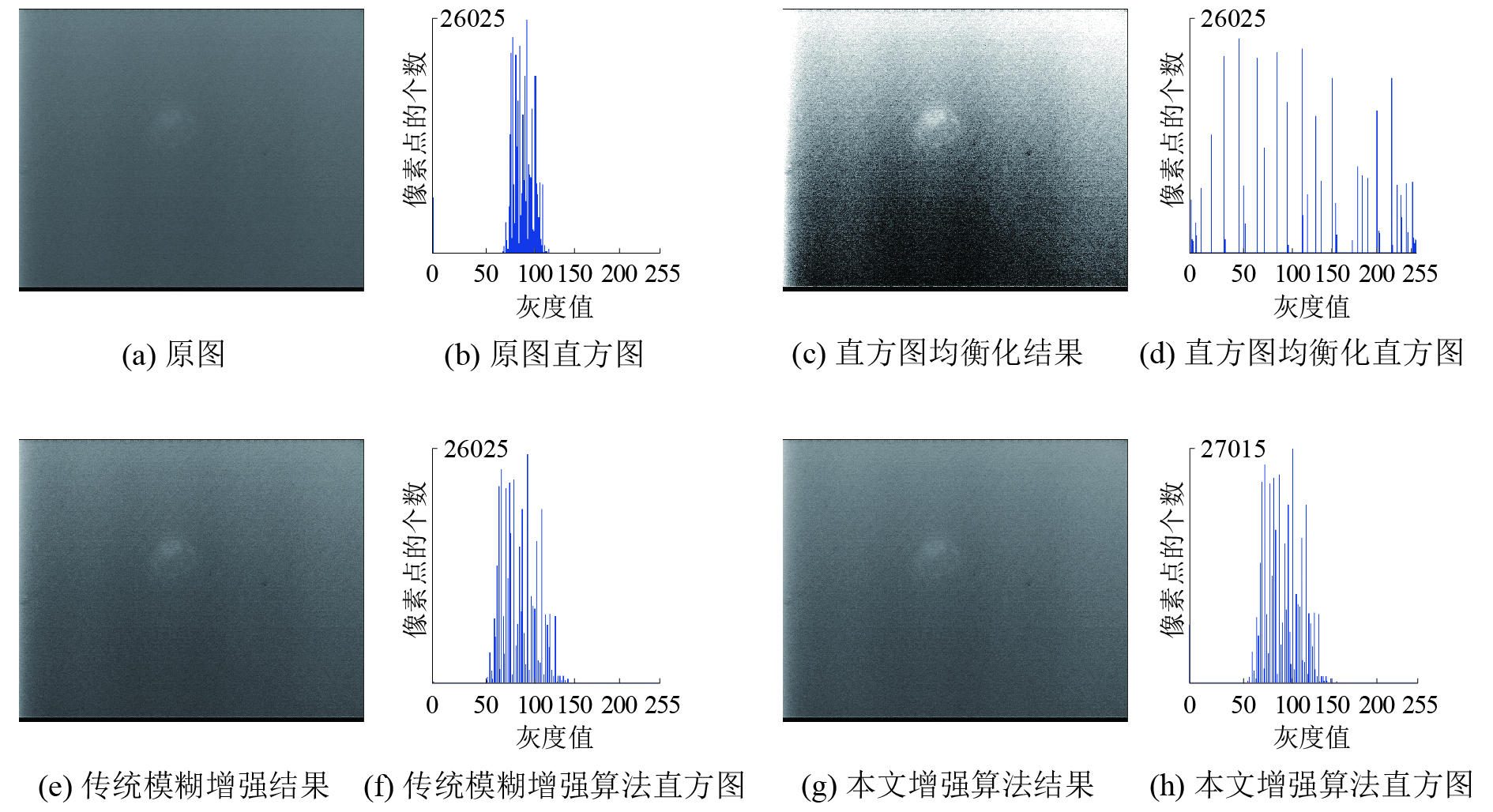
为了验证本文提出的改进增强算法的有效性和快速性，进行了一些对比实验，图4、5分别显示了对水母、水下管道图像分别采用直方图均衡化、传统模糊增强算法、本文增强算法进行处理的结果。

由处理结果可以看出，原图灰度分布的范围较窄。经过直方图均衡化之后，虽然图像的对比度得到改善，但是是它对处理的数据不加选择，处理后的图像增加了背景噪声的对比度并且降低有用信号的对比度，导致变换后图像的灰度级减少，某些细节消失，因此可以看到处理之后图像中噪声更加严重。而对于传统模糊算法，由于其不适用于水下昏暗环境下的图像处理，因此不仅没有达到增强效果，反而增大了图像的灰白效应。而本文改进算法则可以较好地提高背景和水下管道之间的对比度，图像的质量得到了提高，且算法具有较好的适应性。表1给出了对水母、水下管道图像分别采用3种不同增强算法进行处理所需要的时间。

根据处理时间的统计结果可以看出，本文改进的算法较传统的模糊增强算法在速度上有很大提升。综合以上分析，本文改进的增强算法不仅能大大提高处理的速度，还能取得优于传统的模糊增强算法的增强效果。

5 结论

本文以水母和水下管道图像为研究对象，针对水下图像对比度低、效果差、细节模糊、灰白效应等特点，提出一种新的图像降采样方法并改进了模糊增强算法，提高了背景与目标的对比度，实现了强化目标的特征，弱化背景信息的目的。

1) 针对水下图像的特点，为了避免去噪过程中对边缘的平滑作用，引入了图像尺度空间的理论，采用非线性尺度空间的P-M模型，并结合高斯降采样，构造出一种新的图像降采样方法。该方法能在保留图像边缘信息的基础上，实现去噪和尺度缩放功能。

2) 针对水下图像对比度差的特点，本文对传统的模糊增强算法进行了改进，实验验证表明改进的增强算法在提高背景和水下管道之间的对比度方面比传统的模糊增强算法更适合水下管道图像的增强处理。

3) 本文算法为同类图像处理提供了一种高效可行的思路，该算法的自适应能力有待提高，使其能自动分析输入水下图像的数据，针对不同场景及光照条件进行自适应调整，来满足复杂情况需求。