多通道滤波器组理论在雷达、图像、语音信号处理等领域得到了广泛地应用^[1-4]。该技术的使用有效地降低了数据传输速率要求、数据存储空间、数据处理复杂度等。同时在无线电系统中，滤波器组实时在线重构进一步提高了信道划分、切换的灵活性。在实际应用中，为了使滤波器组系统的输入输出信号保持一致性，避免产生相位、幅度、混叠失真，滤波器组应做到完全重构。滤波器组分为均匀滤波器组^[5~7]和非均匀滤波器组。对于均匀滤波器组的设计，文献[5]采用余弦调制的方式来设计均匀滤波器组；文献[6]采用指数调制的方式来设计均匀滤波器组；文献[7]采用另一种设计思路，将重构条件表示为一系列线性方程组，通过迭代解方程组的最优解进而得到各通道滤波器系数。均匀滤波器组对输入信号频带进行均匀划分，而非均匀滤波器组可以根据实际需要将输入信号分割为不同频带宽度的子信号，具有更好的灵活性。对于非均匀滤波器组的设计，文献[8-9]研究了线性相位DFT调制非均匀滤波器组；文献[10]提出了余弦调制非均匀滤波器组。文献[11]采用树型结构结合迭代优化算法^[12~14]，对信号低频分量再分解，实现非均匀滤波器组。以上文献都是通过设计一个原型滤波器，然后再通过滤波器之间的关系设计其他滤波器。本文以一种直接设计的思想，从频域推导了一般性结构滤波器组的输出与输入的关系，根据输入与输出的关系，引申出重构条件，并将其表示为矩阵方程的形式，然后根据给定的滤波器组前端分析模块中各通道的频带分布特性，结合迭代优化思想求解矩阵方程的最优解，进而得出综合模块各通道滤波系数，设计出频带任意划分的均匀或非均匀滤波器组。

1 滤波器组重构条件推导

如图1是滤波器组的一般性结构。

当各通道抽取插值速率 $\left[ {{n_1},{n_2}, \cdots ,{n_{M - 1}}} \right]$ 相同时，该滤波器组称为均匀滤波器组，当 $\left[ {{n_1},{n_2}, \cdots ,{n_{M - 1}}} \right]$ 不全部相等时，该滤波器组称为非均匀滤波器组。此时输出的重构信号 $y\left( n \right)$ 在 $z$ 频域可以表示为

$\begin{aligned}Y\left( z \right) = & \sum\limits_{m = 0}^{M - 1} {\frac{1}{{{n_m}}}{F_k}\left( z \right)\sum\limits_{l = 0}^{{n_m} - 1} {X\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right){H_m}\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right)} } = \\& \sum\limits_{m = 0}^{M - 1} {\frac{1}{{{n_m}}}{F_m}\left( z \right)X\left( z \right){H_m}\left( z \right)} + \\& \sum\limits_{m = 0}^{M - 1} {\frac{1}{{{n_m}}}{F_m}\left( z \right)\sum\limits_{l = 1}^{{n_m} - 1} {X\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right){H_m}\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right)} } = \\& X\left( z \right){T_0}\left( z \right) + \sum\limits_{l = 1}^{{n_m} - 1} {X\left( {z{e^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right){T_l}\left( z \right)} \end{aligned}$

式中：

${T_0}\left( z \right) = \sum\limits_{m = 0}^{M - 1} {\frac{1}{{{n_m}}}{F_k}\left( z \right)} \sum\limits_{l = 0}^{{n_m} - 1} {X\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right){H_m}\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right)} $

(1)

${T_l}\left( z \right) = \sum\limits_{m = 0}^{M - 1} {\frac{1}{{{n_m}}}{F_m}\left( z \right){H_m}\left( {z{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{\pi }}l}}{{{n_m}}}}}} \right)} \;\;\; l = 1,2, \cdots ,M$

(2)

${T_0}\left( z \right)$ 称为整个滤波系统的失真函数，体现了整个滤波系统的幅频相位特性， ${T_l}\left( z \right)$ 称为整个系统的混叠失真函数，对应的混叠信号是 $X\left( {z{{\rm{e}}^{{{ - {\rm{j}}2\pi l} / {{n_m}}}}}} \right)$ 。

当 ${T_0}\left( z \right)$ 是一个纯延迟，即 ${T_0}\left( z \right) = {z^{ - \varDelta }}$ 且 ${T_l}\left( z \right){\rm{ = }}0$ 时，整个系统可实现准确重构，Δ表示时延长度。结合式(1)、(2)，将重构条件表示为矩阵方程的形式，即

${{Ax}} = {{b}}$

(3)

式中： ${{x}}$ 是一个大小为 $MN \times 1$ 的列向量，涵盖了综合模块中 $M$ 个长度为 $N$ 的滤波器系数，即 ${{x}} = {\left[ {{{f}}_1^{\rm{T}},{{f}}_2^{\rm{T}}, \cdots ,{{f}}_M^{\rm{T}}} \right]^{\rm{T}}}$ ； ${{b}}$ 是一个列向量，除了前 $N + \varDelta $ 个元素为1，其他元素均为零。具体表示为

${{{A}}_{L\left( {2N - 1} \right) \times MN}} = \left[\!\!\!\!\! {\begin{array}{*{20}{c}}{{\beta _{1,0}}\Im \left( {{{{h}}_1}} \right)} \!\! & \!\! {{\beta _{2,0}}\Im \left( {{{{h}}_2}} \right)} \!\! & \!\! \cdots & {{\beta _{M,0}}\Im \left( {{{{h}}_M}} \right)}\\{{\beta _{1,1}}\Im \left( {{{{h}}_1} \otimes {{{\varLambda }}_1}} \right)} \!\! & \!\! {{\beta _{2,1}}\Im \left( {{{{h}}_2} \otimes {{{\varLambda }}_1}} \right)} \!\! & \!\! \cdots & {{\beta _{M,1}}\Im \left( {{{{h}}_M} \otimes {{{\varLambda }}_1}} \right)}\\{{\beta _{1,2}}\Im \left( {{{{h}}_1} \otimes {{{\varLambda }}_2}} \right)} \!\! & \!\! {{\beta _{2,2}}\Im \left( {{{{h}}_2} \otimes {{{\varLambda }}_2}} \right)} \!\! & \!\! \cdots & \!\! {{\beta _{M,2}}\Im \left( {{{{h}}_M} \otimes {{{\varLambda }}_2}} \right)}\\ \vdots \!\! & \!\! \cdots \!\! & \!\! \cdots \!\! & \!\! \vdots \\{{\beta _{1,L - 1}}\Im \left( {{{{h}}_1} \otimes {{{\varLambda }}_{L - 1}}} \right)} \!\! & \!\! {{\beta _{2,L - 1}}\Im \left( {{{{h}}_2} \otimes {{{\varLambda }}_{L - 1}}} \right)} \!\! & \!\! \cdots \!\! & \!\! {{\beta _{M,L - 1}}\Im \left( {{{{h}}_M} \otimes {{{\varLambda }}_{L - 1}}} \right)}\end{array}} \!\!\!\!\! \right]$

式中：L是抽取速率 $\left[ {{n_1},{n_2}, \cdots ,{n_{M - 1}}} \right]$ 的最小公倍，定义 ${\alpha _{m,l}}$ 为

${\alpha _{m,l}} = \left\{ {\begin{aligned}& {1,} \quad \quad {{{\rm e}^{{{{\rm j}2\pi * l} / L}}} \in \left\{ {{{\rm e}^{{\rm j}2\pi \left( 1 \right)/{n_m}}},{{\rm e}^{{\rm j}2\pi \left( 2 \right)/{n_m}}}, \cdots ,{{\rm e}^{{\rm j}2\pi \left( {{n_m} - 1} \right)/{n_m}}}} \right\}}\\& {0,} \quad \quad {{\text{其他}}}\end{aligned}} \right.$

β_{m, l}定义为

${\beta _{m,l}} = \left\{ {\begin{array}{*{20}{l}} {{1 / {{n_m},}}}&{l = 0} \\ {{{{\alpha _{m,l}}} / {{n_m},}}}&{l \ne 0} \end{array}} \right.$

(4)

运算符 $\Im$ 定义为

$\Im \left( {{{\left[ {{a_1},{a_2}, \cdots ,{a_N}} \right]}^{\rm{T}}}} \right) = \left[ {\begin{array}{*{20}{c}} {{a_1}}&0&0& \cdots &0 \\ {{a_2}}&{{a_1}}&0& \cdots &0 \\ {{a_3}}&{{a_2}}&{{a_1}}& \cdots &0 \\ \vdots & \cdots & \cdots & \cdots & \vdots \\ {{a_N}}&{{a_{N - 1}}}&{{a_{N - 2}}}& \cdots &{{a_1}} \\ 0&{{a_N}}&{{a_{N - 1}}}& \cdots &{{a_2}} \\ 0&0&{{a_N}}& \cdots &{{a_3}} \\ 0&0&0& \cdots & \vdots \\ 0&0&0& \cdots &{{a_N}} \end{array}} \right]$

${{{h}}_m}\left( {m = 0,2, \cdots ,M - 1} \right)$ 是分析模块中第 $m$ 个通道的滤波器系数，即 ${{{h}}_m} = {\left( {{h_{m,0}},{h_{m,1}}, \cdots ,{h_{m,N - 1}}} \right)^{\rm{T}}}$ 。运算符 $ \otimes $ 表示2个矩阵的对应元素相乘。运算符 ${{{\varLambda }}_i}$ 定义为

${{{\varLambda }}_i} = {\left[ {{{\rm e}^{{{{\rm j}2\pi i \cdot \left( 0 \right)} / L}}} \;\; {{\rm e}^{{{{\rm j}2\pi i \cdot \left( 1 \right)} / L}}} \;\; {{\rm e}^{{{{\rm j}2\pi i \cdot \left( 2 \right)} / L}}} \;\; \cdots \;\; {{\rm e}^{{{{\rm j}2\pi i \cdot \left( {N - 1} \right)} / L}}}} \right]^{\rm{T}}}$

式中 $i = 1, 2\cdots ,L - 1$ 。

此时，定义总的误差函数Q，Q由重构误差Q_PR和幅频误差Q_PR构成，即

$Q = {Q_{{\rm{PR}}}} + {Q_{\rm{MRE}}} = \left\| {{{Ax}} - {{b}}} \right\|_2^2 + \sum\limits_{m = 1}^M {{Q_{{\rm{MRE}},m}}} $

(5)

式中

${Q_{{\rm{MRE}},m}} = \sum\limits_{i = 1}^\rho {\left\| {\left| {{H_m}\left( {{{\rm e}^{{\rm j}w}}} \right)} \right| - {r_m}\left( {{w_i}} \right)} \right\|} _2^2$

(6)

式中： ${\left\| {}* \right\|_2}$ 表示向量2范数， $\rho $ 表示在滤波器通带和阻带内的频率采样点个数， ${r_m}\left( {{w_i}} \right)$ 表示通带、阻带内的理想幅频响应，即

${r_m}\left( {{w_i}} \right) = \left\{ {\begin{array}{*{20}{l}}{1,} & {{w_i}{\text{是}}{H_m}\left( {{{\rm e}^{\rm j}{^w}}} \right){\text{通带内的频率点}}}\\{0,} & {{\text{其他}}}\end{array}} \right.$

从式(4)中可以看出，该方法对于各通道抽取插值速率没有特定的限制，因此可以设计不同形式的滤波器组，提高了滤波器组设计的灵活性。

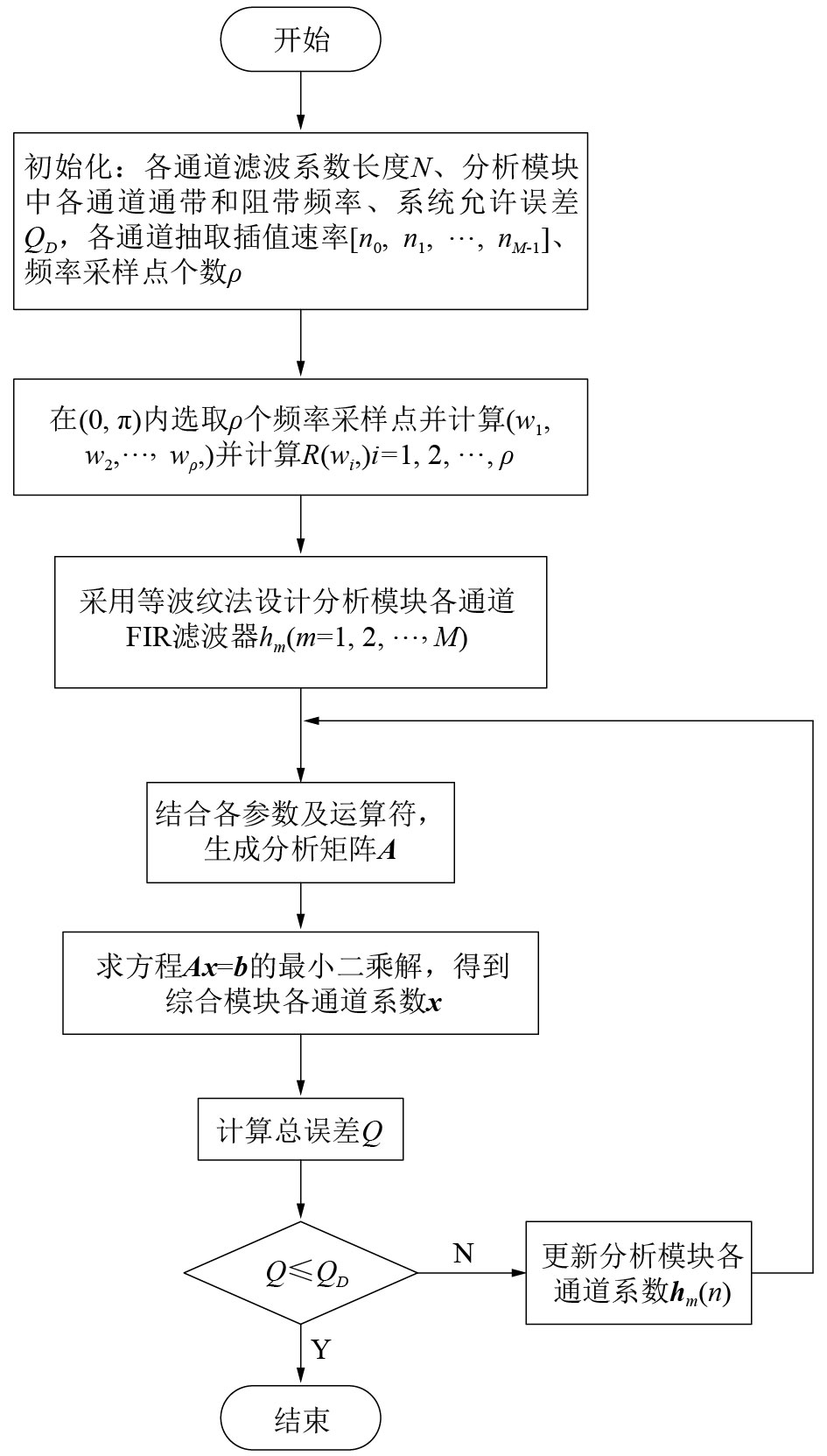
2 滤波器组设计步骤

将误差函数Q设为优化目标函数，将分析模块中各通道滤波系数设为优化参数，通过给定的分析模块各通道频带特性，同时设计分析滤波系数，然后通过求解矩阵方程式(3)的最小二乘解来得到综合模块各通道的滤波器系数。计算误差函数Q，如果误差函数大于给定的误差值，则迭代优化分析模块中各通道滤波系数 ${{{h}}_m} = {\left( {{h_{m,0}},{h_{m,1}}, \cdots ,{h_{m,N - 1}}} \right)^{\rm{T}}}$ ，直到优化目标函数小于给定的误差值Q_D。采用直接法设计滤波器组的具体步骤如下，其流程如图2所示。

1) 初始化各通道滤波器系数长度 $N$ 、分析模块各通道原始FIR滤波器频率特性、需要满足的误差值 ${Q_D}$ 、频率采样点个数 $\rho $ 、各通道抽取插值速率 $\left[ {{n_1},{n_2}, \cdots ,{n_{M - 1}}} \right]$ ，并求出其最小公倍数L；

2) 采用等波纹逼近法设计系统前端分析模块中各通道原始FIR滤波器系数 ${{ h}_m}\left( n \right)\left( {m = 1,2, \cdots ,M} \right)$ ，并结合其他定义参数、运算符生分析矩阵A；

3) 通过求解方程 ${{Ax}} = {{b}}$ 的最小二乘解，得到综合模块中各通道滤波器系数 ${{x}}$ ；

4) 通过式(5)计算误差目标函数Q；

5) 如果求解的误差 $Q$ 小于给定的误差 ${Q_D}$ ，终止该算法，否则通过迭代更新分析模块中的滤波器系数，并返回步骤2)，直到误差 $Q \leqslant {Q_D}$ 。

3 性能仿真

该设计方法可以设计均匀滤波器组，也可以设计非均匀滤波器组。首先采用该设计方法设计一个各通道抽取插值速率为[4, 4, 4, 4]的均匀滤波器组，每个通道滤波器系数长度为54，分析模块中各通道频率特性分布情况如表1所示。

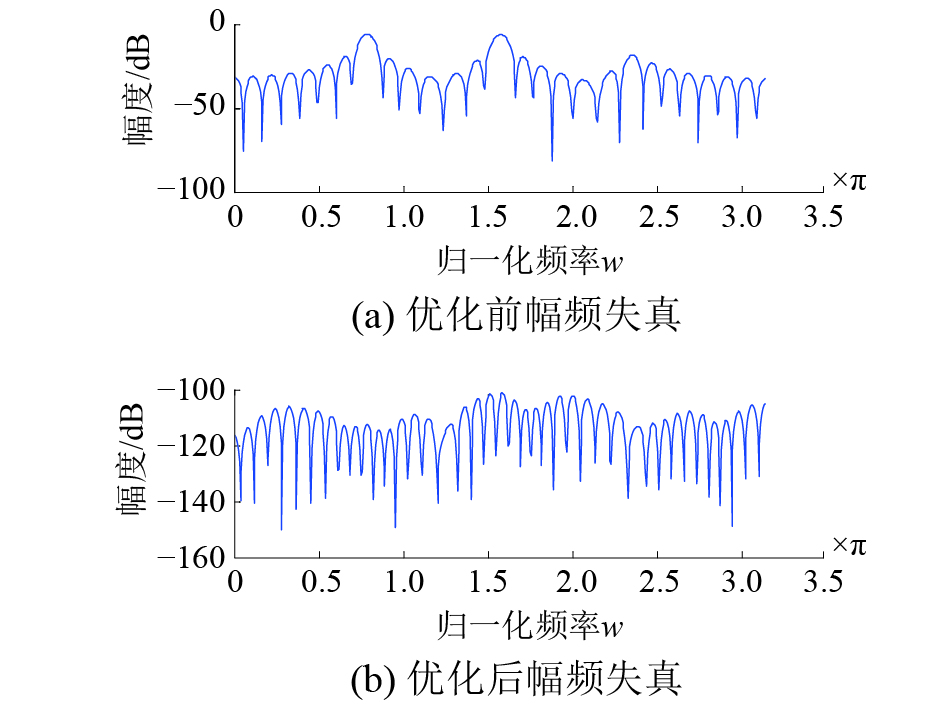
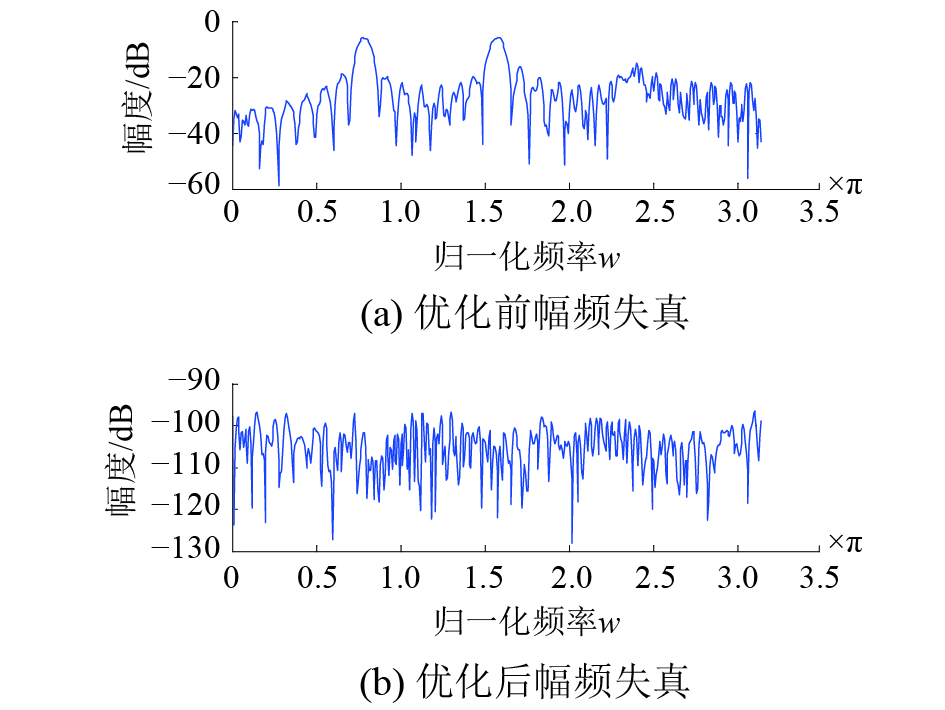
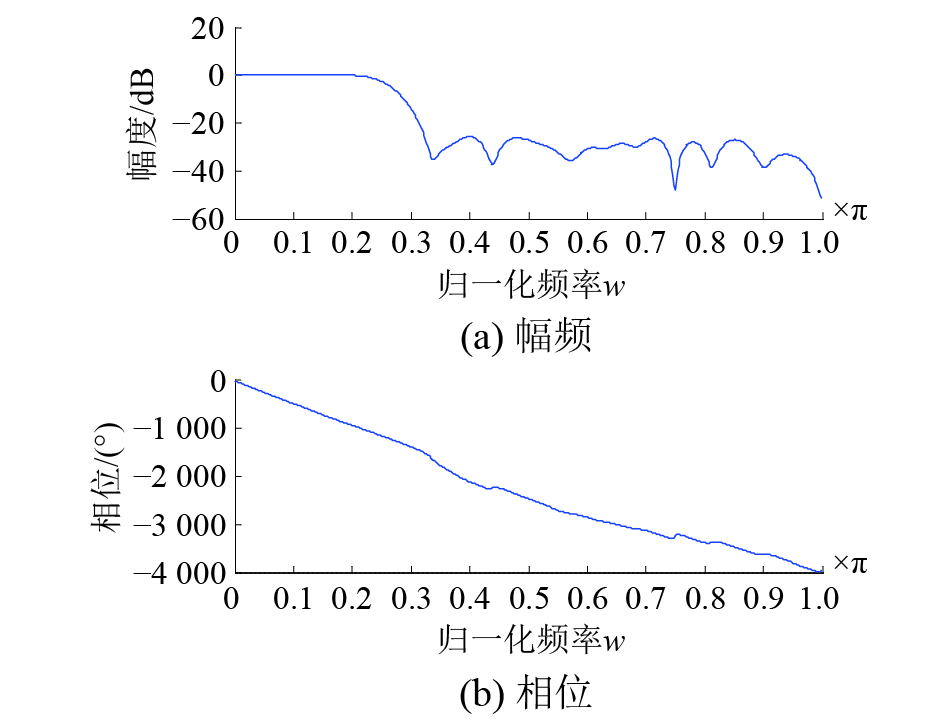
具体的仿真结果如图3~6。在图3中，给出了优化前后整个系统的幅频失真对比情况，图4给出了优化前后整个系统的混叠失真对比情况。可以看出，经过优化，幅频和混叠失真得到了很好的改善。图5所示的是采用该算法设计出的均匀临界采样分析、综合滤波器组。优化之后分析模块中各通道的滤波器系数是满足线性相位特性的，这里给出分析模块中第一通道滤波器系数的幅频相位特性，如图6所示。

另一个例子中，采用该算法设计一个通道个数为4，各通道抽取插值速率分别为[2, 4, 8, 8]的非均匀滤波器组。每个通道滤波器系数长度为64，分析模块中各通道频率特性分布情况如表2所示。

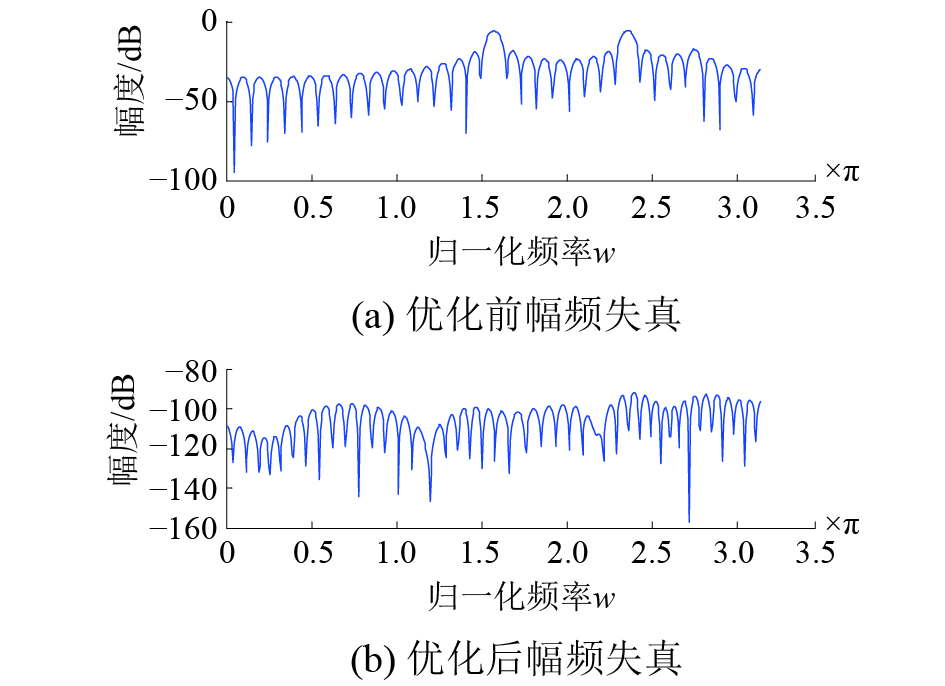
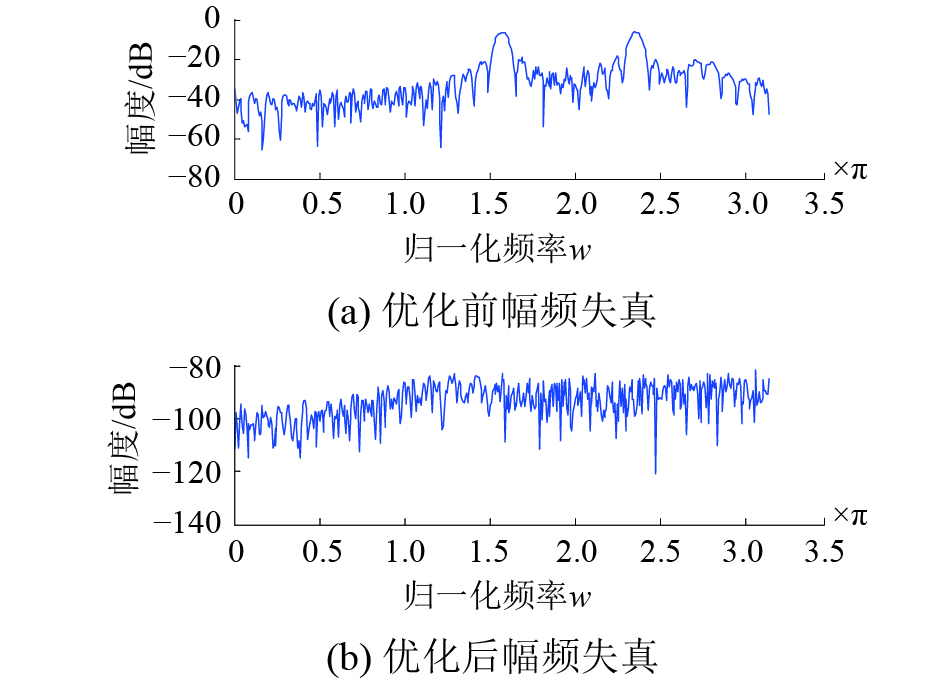
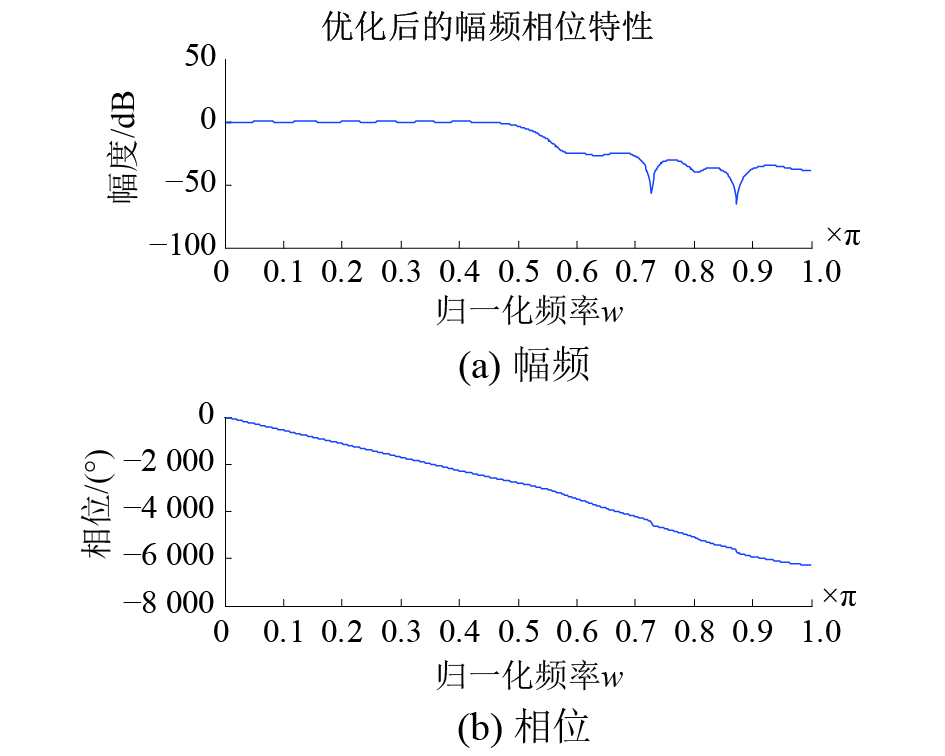
具体仿真如图7~10。图7、8分别给出了整个滤波系统在优化前后的幅频、混叠失真对比情况。图9所示的是采用该算法最终设计出的非均匀滤波器组。优化之后分析模块中各通道的滤波器系数是满足线性相位特性的，这里给出分析模块中第一通道滤波器系数的幅频相位特性，如图10所示。

4 结论

本文采用直接法设计滤波器组，推导了图1所示的一般性结构滤波器组的重构条件，并将重构条件以矩阵方程的形式表示。采用迭代优化的思想求解矩阵方程的最优解，进而设计出滤波器组。从仿真分析可知：1)该设计方法可以同时设计均匀和非均匀的滤波器组，可以对频带进行不同的划分，与现有设计方法相比，具有很高的灵活性；2)采用该方法设计的滤波器组，整个滤波系统分析模块中的滤波系数具有线性相位特性，避免了相位失真。