无源互调(passive intermodulation,PIM)是在卫星、雷达等通信系统中常见的一类干扰信号,当复数个载波信号通过无源器件时,由于器件固有的部分弱非线性特质,其输出信号将包含各载波混频的产物,并恶化接收系统的通信质量。随着通信系统的可利用频谱越来越窄,功率容量日渐增大,PIM效应也显著增强,使得其成为了限制系统发展的主要瓶颈之一[1-3]。引发PIM的根源种类繁多,大致可归类为两种:接触非线性和材料非线性[4]。接触非线性是指具有非线性电流和电压特性的电接触,比如金属焊接和裂缝、金属-氧化物-金属连接等[5];材料非线性是指具有固有非线性电特性的材料,如铁磁体、等离子体、热敏电阻等。从多物理场的角度来说,器件由于温度变化而出现的众多非线性效应也是产生PIM的潜在因素。文献[6]从电热耦合效应的角度研究了阻性器件的PIM问题,文献[7]提出了基于热电子发射效应的波导结非线性无源互调模型。总的来说,关于热效应致PIM的研究相对较少。这主要是因为大部分通信系统的工作频率都很高,同时材料对于热的响应往往要慢于电响应[4],使得整个多物理场的耦合过程极为复杂,加大了研究难度。在工程实践中,热效应广泛存在,目前已观察到许多PIM随温度变化而变化的现象。如果系统设计合理,各接触部件连接良好,热效应导致的PIM将取代其他类型的PIM成为系统主要的干扰源[8],因而急需对相关热致PIM机理进行更加深入的研究。
当系统中存在2个频率间隔较小的输入信号时,介质材料的周期性吸热放热将使器件发生热致振动,并在系统中引入PIM。本文在提出这种新机理的基础上,用多物理场仿真软件对相关推导场景进行仿真验证,最后根据理论设计并完成了波导传输线实验,证实了此类PIM的存在。
1 热致振动引起的无源互调拍现象[9](或差拍现象)是振动合成过程中的一种特有现象,它在光学、声学、电磁学领域都有重要的应用。在微波频段,当2个频率相近的微波信号在有耗介质中传输时,由拍现象理论可知,其总电场幅度会随2个信号的包络变化,其变化周期与2个信号的差频相关。假设2个信号分别为
| $\left\{ \begin{aligned}& {u_1}\left( t \right) = {V_1}\cos \left( {{\omega _1}t{\rm{ + }}{\theta _{\rm{1}}}} \right)\\& {u_{\rm{2}}}\left( t \right) = {V_{\rm{2}}}\cos \left( {{\omega _{\rm{2}}}t{\rm{ + }}{\theta _{\rm{2}}}} \right)\end{aligned} \right.$ |
式中:V1、V2分别是2个信号的振幅,ω1、ω2为角频率,θ1、θ2为初始相位。
那么总电场为
| $\begin{aligned}u = & {u_1}\left( t \right) + {u_{\rm{2}}}\left( t \right) = {V_1}\cos \left( {{\omega _1}t{\rm{ + }}{\theta _{\rm{1}}}} \right) + {V_{\rm{2}}}\cos \left( {{\omega _{\rm{2}}}t{\rm{ + }}{\theta _{\rm{2}}}} \right) = \\& \sqrt {V_1^2 + V_2^2 + 2{V_1}{V_{\rm{2}}}\cos \left[ {\left( {{\omega _1} - {\omega _{\rm{2}}}} \right)t + {\theta _{\rm{1}}} - {\theta _{\rm{2}}}} \right]} \times \\& \sin \left( {\frac{{{\omega _1} + {\omega _{\rm{2}}}}}{2}t + \frac{{{\theta _{\rm{1}}} + {\theta _{\rm{2}}}}}{2} + \varphi } \right)\end{aligned}$ | (1) |
式中
由式(1)可知,合成电场的幅度变化具有周期性,其周期等于差频的倒数,同样的,介质中由电损耗带来的热功率的变化规律也如此。
热功率的变化将使介质温度发生波动,热功率和温度之间的函数关系可以表示为
| $T({ r},t) = f({P_{{\rm{Loss}}}},{\omega _{{\rm{IM}}}}t)$ |
式中:
| $T = {T_0} + at + b\sin \left( {{\omega _{\rm IM}}t} \right)$ | (2) |
式中:T0是介质初始温度;at是温度线性项;b是温度的周期振幅量,与输入信号和材料特性相关。当达到热平衡后,温度的线性项变为常数。
对于绝大多数材料而言,温度的波动将引发热胀冷缩,如果温度场的梯度急剧变化,甚至会引发热致振动[10]。例如周期性飞过日照区和阴影区的在轨卫星,很容易因温度变化产生热致振动。根据热力学相关理论[11],器件温度波动的振幅越大,即温差越大,热膨胀(收缩)的幅度也就越大。对于微波传输线而言,热致振动将在微观层面改变器件的尺寸,导致器件特征阻抗发生变化。因此其特征阻抗Z0(ωIM)可以表示为
| ${Z_0}({\omega _{{\rm{IM}}}}) = {Z_0} \cdot g({P_{{\rm{Loss}}}},\alpha ,{\omega _{{\rm{IM}}}}t)$ |
式中:α是材料热膨胀系数,Z0是传输线初始特征阻抗。
特征阻抗的变化将进一步改变线上的电压和电流,并在输入阻抗Zin(ωIM)中引入周期性变化:
| ${Z_{{\rm{in}}}}\left( {{\omega _{{\rm{IM}}}}} \right) = {Z_0}({\omega _{{\rm{IM}}}})\frac{{{Z_L} + {Z_0}({\omega _{{\rm{IM}}}})\tan (\beta l)}}{{{Z_0}({\omega _{{\rm{IM}}}}) + {Z_L}\tan (\beta l)}}$ |
式中:β是相位常数,l是输入端到负载的距离,ZL是负载阻抗。最终,微带线上非线性的电压和电流将导致无源互调的产生。
2 仿真建模分析下面利用多物理场仿真软件COMSOL进行波导仿真,以BJ-22型波导为原型建模,传输微波频率分别为f1=2.4 GHz和f2=2.5 GHz,仿真计算波导窄边壁上中心点A处在双频微波输入下的温度和电场变化,模型二维简化图如图1所示。

|
Download:
|
| 图 1 模型二维简化 | |
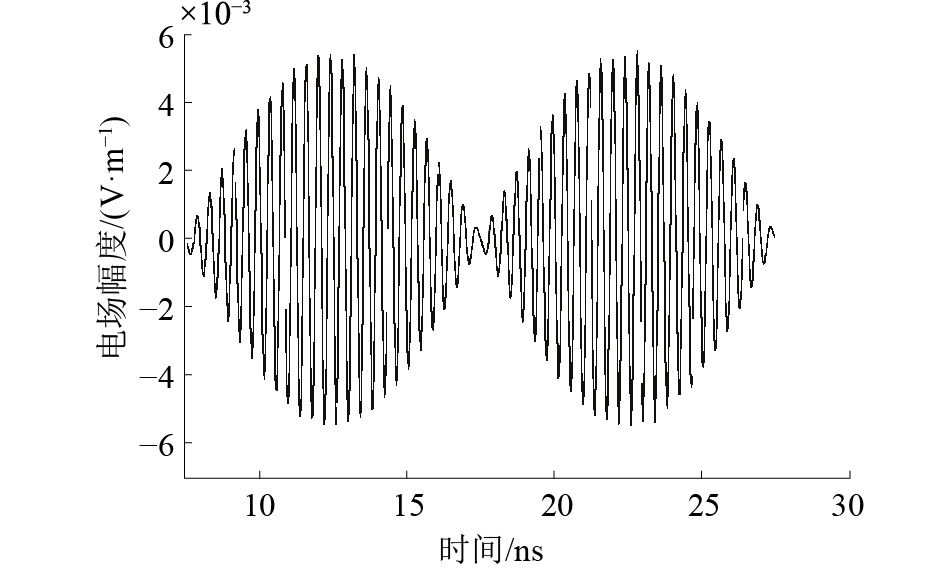
A点的电场变化如图2所示,电场的包络随2个信号差频变化;A点温度变化如图3所示,温度变化以差频(100 MHz)的倒数(10 ns)为周期波动上升,与式(2)符合良好。由此可以看出,在双频微波输入下,波导因损耗导致的温升包含一个周期波动项,从而使波导壁产生热致振动。
|
Download:
|
| 图 2 A点电场变化 | |

|
Download:
|
| 图 3 A点温度变化 | |
波导壁的膨胀和收缩将导致波导宽边尺寸a发生改变,进而在传输线特征阻抗Zw中引入非线性,并有如下关系:
| $\frac{{\Delta {Z_w}}}{{{Z_w}}} = - \frac{{{\lambda ^2}}}{{4{a^2} - {\lambda ^2}}}\frac{{\Delta a}}{a}$ |
式中:λ是工作波长,ΔZw是特征阻抗变化量,Δa是宽边热振动幅度,与温度振幅量b、热膨胀系数α等有关。ΔZw与Δa成正比关系,说明热振动越剧烈,波导阻抗非线性越强,PIM功率也就越大。为了模拟波导壁的非线性振动,我们设置模型中宽边尺寸a为变量,并让其包含一个以差频为角频率的波动项,调整输入功率并适当放大a中的非线性系数,继续仿真A点的电场变化。
A点电场变化如图4所示。

|
Download:
|
| 图 4 引入非线性后的A点电场变化 | |
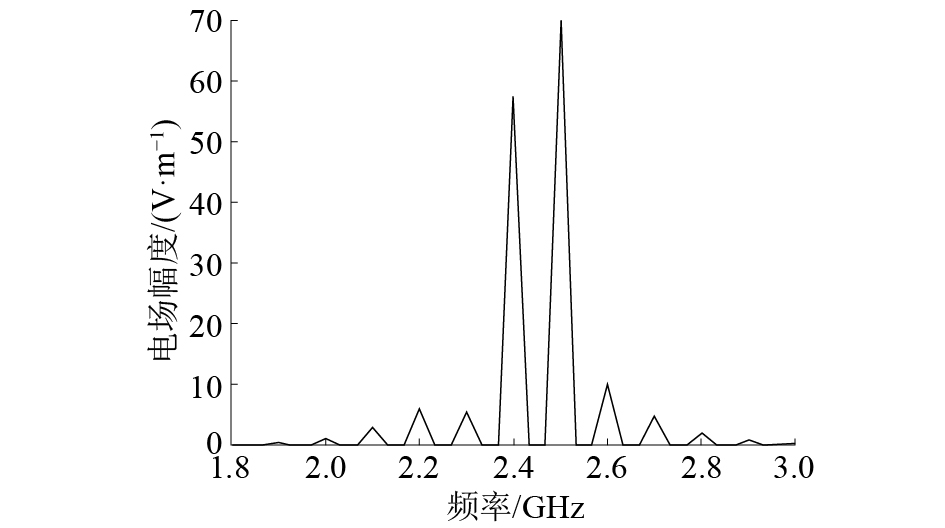
可见电场包络仍随差频周期变化,将电场做快速傅里叶变换(fast Fourier transformation,FFT)后得到频域结果如图5所示。在频谱上除了基频分量,也出现了3阶、5阶等互调频率分量,说明特性阻抗的非线性变化会引入PIM。
|
Download:
|
| 图 5 A点电场FFT变换频域结果 | |
在射频和微波频段,电流由于趋肤效应主要集中在导电材料表面,材料损耗产生的热量将引发温度变化,同时趋肤层的微小热源会热胀冷缩,迫使整个部件作强迫振动。在相同的输入功率下,对于不同窄边壁厚的BJ-22型波导来说,损耗产生的热能是相等的,根据相关矩形厚板振动计算模型分析[12],波导壁越厚,热致振动效应越弱,相应产生的PIM功率也更小。
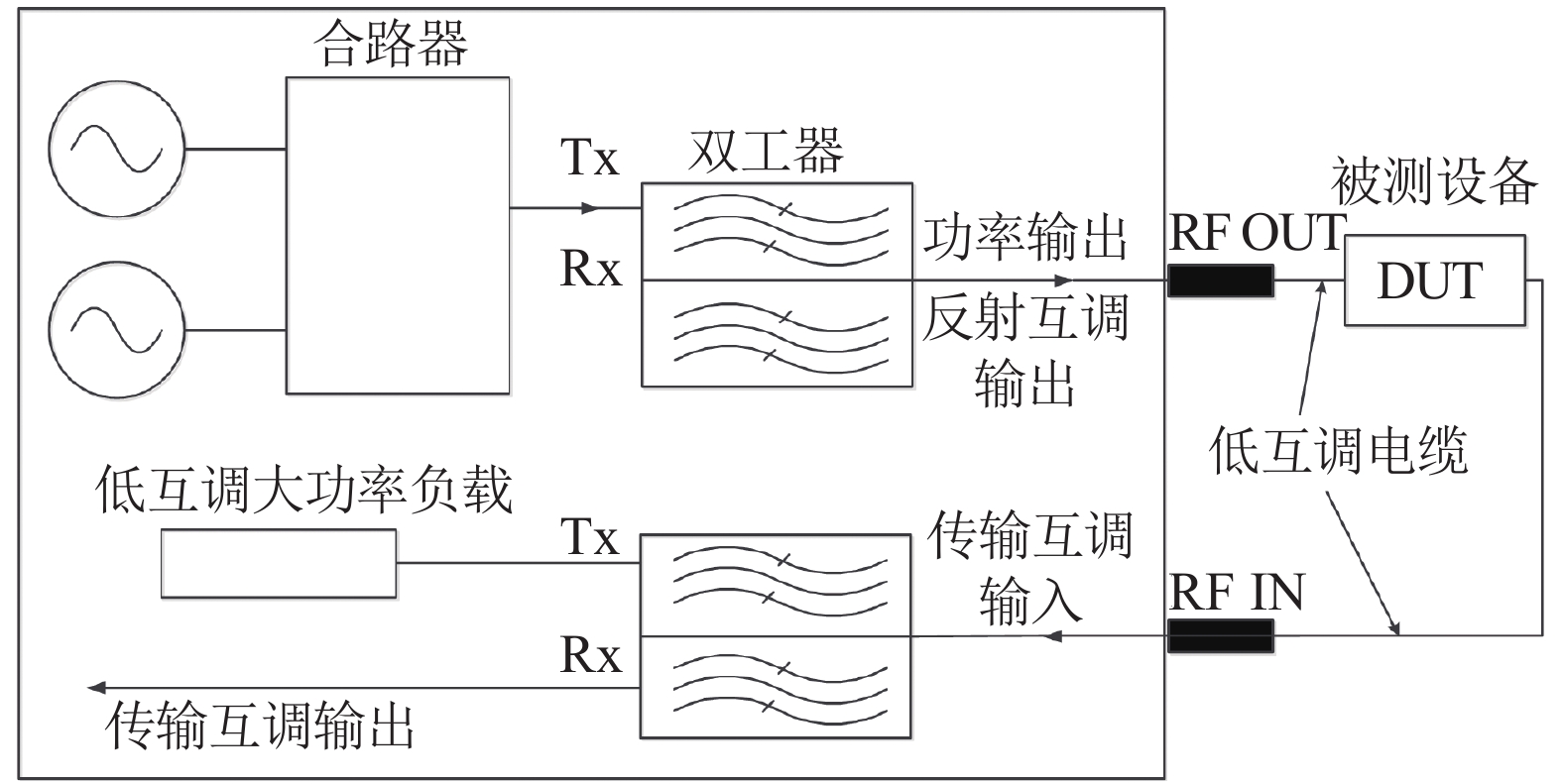
因此实验中的待测BJ-22型波导仅壁厚不一致,通过测量不同器件的PIM相对强弱就可验证热振动致PIM效应。具体实验系统如图6所示。
|
Download:
|
| 图 6 PIM测试系统 | |
所用波导材质为不锈钢,波导和法兰使用一体式加工,中间未焊接,避免因焊接而在接触面引入其他形式的PIM,同时在波导和波同转换两器件接触面加入聚酰亚胺薄膜,削弱该处的接触PIM。图7为实际测量所用波导和波导同轴转换。窄边壁厚分别为0.5、1和2 mm,宽边厚度皆为2 mm。输入微波频率分别为2 161 MHz和2 174 MHz,测试的9阶PIM频率为2 109 MHz。实验中每一路微波输入功率同时从47 dBm变化到53 dBm,每隔1 dBm测量一次波导PIM功率,并在同轴直连的情况下对系统噪声功率进行测量。

|
Download:
|
| 图 7 实际测量所用波导和波导同轴转换 | |
实验测量结果如图8所示,当输入功率不大于49 dBm的时候,3个波导的互调功率缓慢提升,但互相之间差异并不明显,同时波导PIM功率和系统噪声功率相差在1.8 dB以内,说明此时波导热振动不明显,相应PIM较弱。

|
Download:
|
| 图 8 9阶传输PIM功率测量结果 | |
当输入功率大于49 dBm的时候,3个波导的PIM功率开始随输入功率的增大而显著提升,功率上升曲线斜率不小于2.13,波导PIM功率比系统噪声功率至少大2 dB,说明此时测量到的功率信号是由波导自身互调产生的。
在波导的PIM功率曲线的后半段,存在很明显趋势,即相同输入功率下,0.5 m不锈钢波导PIM最强,1 mm不锈钢波导PIM次之,2 mm不锈钢波导PIM最弱。结合前面的分析,充分说明了热振动PIM是存在的,其非线性来源于不锈钢波导壁的热致振动,且壁越薄,热振动越强,相应的PIM功率越大。
5 结论本文提出了一种基于热致振动产生无源互调的新机理,初步分析了此无源互调与温度波动的关系,然后利用多物理场仿真软件对相关物理过程进行仿真探究,最后利用波导传输线在S波段进行了实验验证,结果表明:
1) 该PIM效应在大功率条件下表现显著。当实验系统的输入微波功率较低时,3种窄边厚度不同的波导互调功率无显著差异,说明此时热致振动PIM不占主导地位。而当微波功率提高时,在其他参数相同的条件下,随着波导发热量的增加,热致振动变强,开始与其他类型的PIM区分开。
2) 该PIM效应确实存在,其强弱和热振动振幅有正相关关系。理论上波导壁越薄,越容易产生振动,进而传输线阻抗非线性增强,其PIM功率就越大,随后的波导实验的中也观察到了此类现象,这也定性验证了该PIM机理的正确性。
本文仅对比分析了不同条件下此类PIM的强弱关系,缺乏相应的定量分析。今后研究的方向可以从理论角度给出更多的定量结果,结合实验验证,并提出相应的PIM抑制手段。
| [1] |
LIU P L. Passive intermodulation interference in communication systems[J]. Electronics & communication engineering journal, 1990, 2(3): 109-118. ( 0) 0)
|
| [2] |
SHASTRY S V K, HARIHARAN V K, WARA T, et al. Passive intermodulation in microwave space systems[J]. IETE technical review, 2001, 18(6): 455-474. DOI:10.1080/02564602.2001.11416996 ( 0) 0)
|
| [3] |
张世全, 傅德民, 葛德彪. 无源互调干扰对通信系统抗噪性能的影响[J]. 电波科学学报, 2002, 17(2): 138-142. ( 0) 0)
|
| [4] |
叶鸣, 贺永宁, 孙勤奋, 等. 大功率条件下的无源互调干扰问题综述[J]. 空间电子技术, 2013, 10(1): 75-83. ( 0) 0)
|
| [5] |
江伟健, 赵洪, 李家林, 等. 波导法兰盘连接结MIM结构的研究[C]//2013年全国微波毫米波会议论文集. 重庆, 中国, 2013.
( 0) 0)
|
| [6] |
SHITVOV A, SCHUCHINSKY A G, STEER M B, et al. Characterisation of nonlinear distortion and intermodulation in passive devices and antennas[C]//Proceedings of the 8th European Conference on Antennas and Propagation. Hague, Netherlands, 2014: 1454-1458.
( 0) 0)
|
| [7] |
叶鸣, 贺永宁, 孙勤奋, 等. 基于热电子发射非线性的波导结无源互调机理研究[J]. 空间电子技术, 2012, 9(3): 55-57, 70. ( 0) 0)
|
| [8] |
王斌. 微波频段无源互调干扰研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
( 0) 0)
|
| [9] |
贺小龙, 张立民, 邱飞力, 等. 内燃动车组辅助机组拍振现象分析[J]. 噪声与振动控制, 2016, 36(1): 83-87, 105. ( 0) 0)
|
| [10] |
SHEN Zhenxing, HU Gengkai. Thermally induced vibrations of solar panel and their coupling with satellite[J]. International journal of applied mechanics, 2013, 5(3): 1350031. DOI:10.1142/S1758825113500312 ( 0) 0)
|
| [11] |
李林, 李映辉, 袁继禹. 基于有限元方法的空气预热器转子热位移分析[J]. 重庆理工大学学报, 2016, 30(10): 49-54. ( 0) 0)
|
| [12] |
张羽飞, 杜敬涛, 杨铁军, 等. 任意边界条件三维弹性矩形厚板结构振动分析[J]. 哈尔滨工程大学学报, 2015, 36(11): 1448-1453, 1531. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


