软件无线电概念自20世纪90年代提出以来,便在电子信息、移动通信及计算机等领域引起了广泛关注,并推动了电子领域的快速发展。基于软件无线电技术的雷达发射机,以数字信号处理为核心,以FPGA、DSP等各种微电子数字芯片为硬件基础。不同于传统的雷达发射机,软件无线电雷达发射机基于某种架构协议,这样软件、硬件部分有一种通用的“语言”,使雷达波形和处理算法软件化、可编程、可升级,达到了可重构目的,从而提高了雷达的功能和性能,应用前景十分广泛[1]。
在雷达发射机系统中常常要产生大瞬时带宽的雷达信号,而FPGA、DSP等数字信号处理芯片的处理速度无法满足要求,这时可以通过多通道信道化技术解决这个问题。要产生带宽较宽的雷达信号,可以先分别在低频带上产生子带信号,再通过子带信号的合成得到所要发射的雷达信号。另外,我们通过信道化技术可以只用一部发射机同时发射多个信号,这样一部发射机能实现多部发射机的功能,大大降低了发射机的成本和体积,而发射机的频谱资源也得到了充分利用。因此,我们也可以通过信道化将雷达信号与通信信号占用不同的带宽发射出去,实现雷达与通信平台、资源共享,为雷达通信一体化设计提供了可行途径[2]。本文最后通过MATLAB仿真实验验证了信道化发射机解决上述问题的可行性。
1 多通道信道化雷达发射机结构设计 1.1 信道化发射机基本数学模型实际应用中雷达发射机只能发射实信号,而复信号输出多在理论分析中应用。以实信号输出为例,我们假设有待发射的I个基带信号
| ${\omega _i} = \frac{{2{\rm{\pi }}}}{I}\left( {i + \frac{1}{4}} \right)\left( {i = 0,1, \cdots ,I - 1} \right)$ | (1) |
最后把处理输出后的I路移频信号相加,最后取实部即得发射信号
|
Download:
|
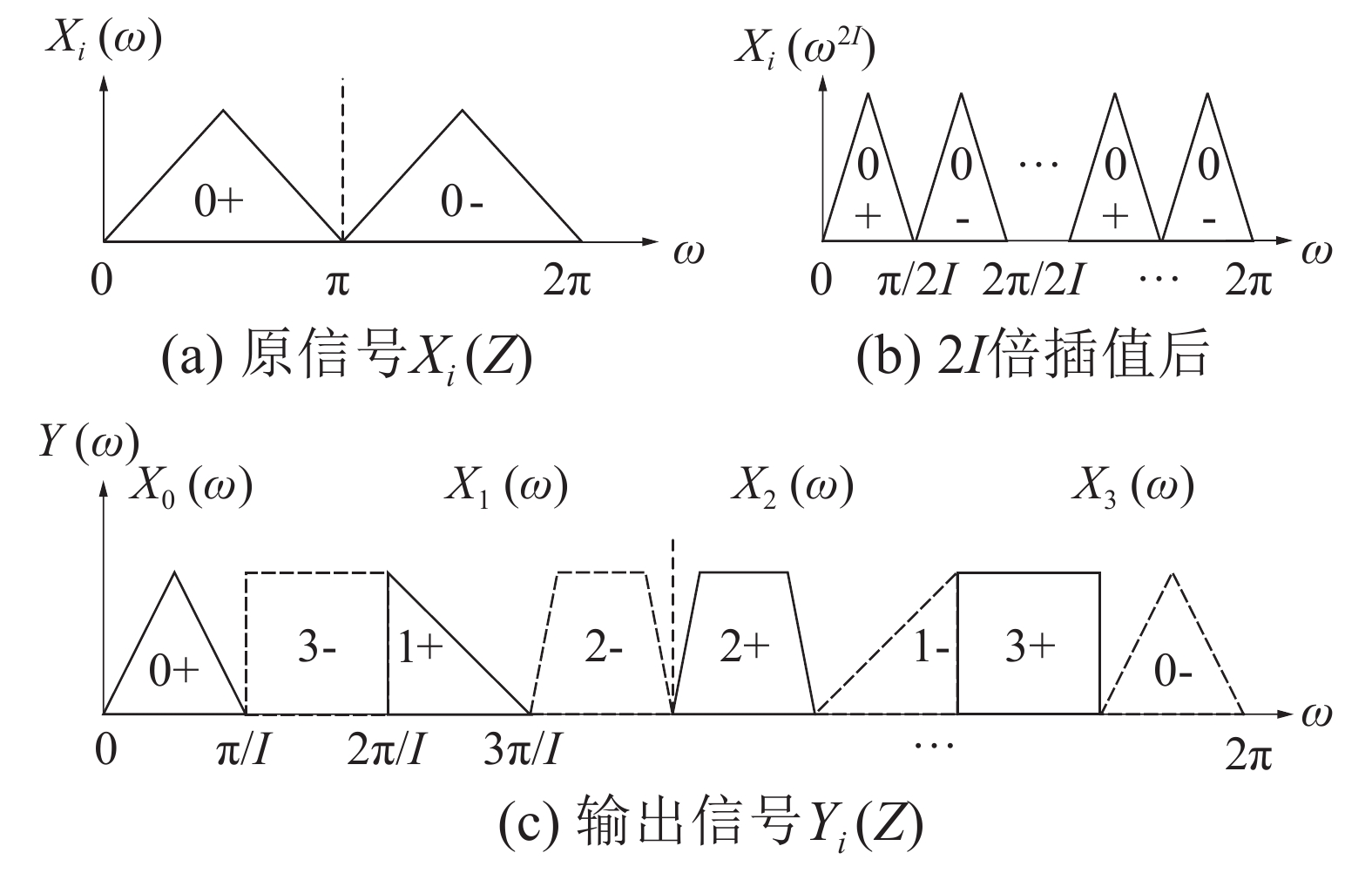
| 图 1 实信号输出发射机频谱搬移过程(I=4) | |
为了避免信号经信道化后发生混叠失真,我们必须给每个信道留一段带宽存放输出取实部后产生的实频带所对应的共轭对称分量。如图1(c)所示,图中虚线频带便是存放实频带所对应的共轭对称分量。若输入信号采样频率为

|
Download:
|
| 图 2 实信号输出信道化发射机结构(直接移频法) | |
图2中是实信号输出信道化发射机的基本模型,体现了发射机信道化的思想,但是结构复杂,计算效率不高、实时处理能力弱。因此,我们推导一种高效的多相滤波信道化发射机结构模型。
由图2可得:
| $\begin{aligned}& y\left( n \right) = \mathop \sum \limits_{i = 0}^{I - 1} {y_i}\left( n \right) = \mathop \sum \limits_{i = 0}^{I - 1} \left[ {{{x'}_i}\left( n \right) * h\left( n \right)} \right]{{\rm{e}}^{{\rm{j}}{\omega _i}n}} = \\& \quad \quad \quad \mathop \sum \limits_{i = 0}^{I - 1} \left[ {\mathop \sum \limits_{k = - \infty }^{ + \infty } {{x'}_i}\left( k \right)h\left( {n - k} \right)} \right]{{\rm{e}}^{{\rm{j}}{\omega _i}n}}\end{aligned}$ | (2) |
式中
| ${x'_i}\left( k \right) = \left\{ {\begin{array}{*{20}{l}}{{x_i}\left( {\displaystyle\frac{k}{{2I}}} \right),\left( {k = 0, \pm 2I, \pm 4I, \cdots } \right)}\\{0,\;\;\;\;\;\;\;\;\;\;\;{\text{其他}}}\end{array}} \right.$ |
令
| $n = rI + l\;\;\;\;\;\left( {r = \left( { - \infty , + \infty } \right),l = 0,1,2, \cdots ,I - 1} \right)$ |
则
| $\left\{ \begin{array}{l}y\left( {rI + l} \right) = {y_l}\left( r \right)\\h\left( {rI + l} \right) = {h_l}\left( r \right)\end{array} \right.$ | (4) |
将式(3)代入式(2)得:
| $\begin{aligned}& {y_l}\left( r \right) = y(rI + l) = \mathop \sum \limits_{i = 0}^{I - 1} \left[ {\mathop \sum \limits_{k = - \infty }^{ + \infty } {x_i}\left( k \right)h\left( {rI + l - 2kI} \right)} \right]{{\rm{e}}^{{\rm{j}}{\omega _i}\left( {rI + l} \right)}} = \\& \;\;\;\;\;\;\;\;\;\;\;\mathop \sum \limits_{k = - \infty }^{ + \infty } \left[ {\mathop \sum \limits_{i = 0}^{I - 1} {x_i}\left( k \right){h_l}\left( {r - 2k} \right)} \right]{{\rm{e}}^{{\rm{j}}{\omega _i}rI}} \cdot {{\rm{e}}^{{\rm{j}}{\omega _i}l}}\end{aligned}$ | (5) |
将式(1)代入式(4)得:
| ${y_l}\left( r \right) = \mathop \sum \limits_{k = - \infty }^{ + \infty } \left[ {\mathop \sum \limits_{i = 0}^{I - 1} {x_i}\left( k \right) \cdot {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{\pi }}}}{I}il}}} \right]{{\rm{e}}^{{\rm{j}}r\frac{{\rm{\pi }}}{2}}} \cdot {{\rm{e}}^{{\rm{j}}\frac{{\rm{\pi }}}{{2I}}l}} \cdot {{\rm{e}}^{{\rm{j}}2{\rm{\pi }}ir}} \cdot {h_l}\left( {r - 2k} \right)$ |
式中:
| $\left[ {\mathop \sum \limits_{i = 0}^{I - 1} {x_i}\left( k \right) \cdot {{\rm{e}}^{{\rm{j}}\frac{{{\rm{2\pi }}}}{I}il}}} \right] = {\rm{IDFT}}\left[ {{x_i}\left( k \right)} \right]$ |
定义:
| ${g_l}\left( k \right) = {\rm{IDFT}}\left[ {{x_i}\left( k \right)} \right]$ |
则:
| ${y_l}\left( r \right) = \mathop \sum \limits_{k = - \infty }^{ + \infty } \left[ {{g_l}\left( k \right)\cdot{{\rm{e}}^{{\rm{j}}\frac{{\rm{\pi }}}{{2I}}l}}} \right]{{\rm{e}}^{{\rm{j}}r\frac{{\rm{\pi }}}{2}}} \cdot {h_l}\left( {r - k} \right)$ |
令:
| ${g_l}^\prime \left( k \right) = \left[ {{g_l}\left( k \right)\cdot{{\rm{e}}^{{\rm{j}}\frac{{\rm{\pi }}}{{2I}}l}}} \right]$ |
设
| ${g_l}^{\prime \prime }\left( k \right) = \left\{ {\begin{array}{*{20}{l}}{{g_l}^\prime \left( {\displaystyle\frac{k}{2}} \right),\;\;\;\;\left( {k = 0, \pm 2, \pm 4, \cdots } \right)}\\{0,\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{其他}}}\end{array}} \right.$ |
| $\begin{split}& {y_l}\left( r \right) = \sum\limits_{k = - \infty }^{ + \infty } {{g_l}^\prime } \left( k \right) \cdot {h_l}\left( {r - 2k} \right)] \cdot {{\rm{e}}^{{\rm{j}}r\frac{\pi }{2}}} = \\& [\sum\limits_{k = - \infty }^{ + \infty } {{g_l}^{\prime \prime }} \left( k \right) \cdot {h_l}\left( {r - k} \right)] \cdot {{\rm{e}}^{{\rm{j}}r\frac{\pi }{2}}} = [{g_l}^{\prime \prime }\left( r \right) \cdot {h_l}\left( r \right)] \cdot {{\rm{e}}^{{\rm{j}}r\frac{\pi }{2}}}\end{split}$ |
最后可得:
| $y\left( n \right) = {y_l}\left( {\frac{{n - l}}{I}} \right)$ |
式中的
由以上推导得,实信号的多相结构信道化发射机模型如图3所示。

|
Download:
|
| 图 3 实信号输出的多相结构信道化发射机模型 | |
在抽样速率转换时存在许多不必要的零乘运算,而我们推导的多相结构则可以避免这些无意义的运算,大大提高了运算速率。另外,其中的离散傅里叶变换(inverse discrete Fourier transform, IDFT)运算由于存在快速算法,所以计算量将进一步减少,实时处理能力进一步加强。文中我们以算法中的乘法数量作为复杂度的衡量指标[5],当2种模型运算输出一个数据时,需要的乘法数量为:
1) 直接移频法信道化发射机:
2) 多相滤波结构信道化发射机:
由以上分析可知,随着信道数I的增大,多相结构的信道化发射机计算量将明显小于直接移频法的信道化发射机。
2 基于SDR的雷达发射机实现框架 2.1 硬件实现框架SCA作为软件无线电的一种标准规范,通过把应用与底层软硬件分开的分层设计,保证了软件无线电硬件设备的通用性和系统的开放性及移植性。将高速处理和并行运算可重构芯片FPGA融入系统中,是雷达发射机实现的关键[6-7]。另外,软件无线电系统采样模块化结构,软硬件的可移植性及互操作性强,可实现多模式切换,实现了软件的可重构性,是未来发展的趋势。基于SCA架构的雷达发射机系统兼具硬件的性能和软件的灵活性,可以快速地适应时变的环境和波形切换或参数设置要求[8-9],其框架如图4所示。

|
Download:
|
| 图 4 基于SDR可重构多通道雷达发射机实现框架 | |
对于多相结构的信道化发射机的硬件实现,综合考虑软件无线电的解决方案,根据功耗、成本、处理速度等各方面考虑,采用FPGA设计信道化发射机相比于其他器件优势明显。根据图3中的多相结构信道化发射机实现结构可得,FPGA中的实现框图具体如图5所示。多相结构信道化发射机FPGA实现主要分为IDFT设计、并行滤波器设计、复数乘法设计、内插及延时相加等4部分[10]。

|
Download:
|
| 图 5 多相结构信道化发射机FPGA实现 | |
图中IDFT实现可采用其高效算法快速傅里叶反变换(inverse fast Fourier transform, IFFT)来实现,在Xilinx ISE中的FPGA中可以调用FFT/IFFT的IP Core完成此设计,我们可以根据需要设置FFT通路数、点数、工作时钟和实现结构。而多相结构FIR滤波器设计可以将MATLAB中计算好的原型滤波器系数保存成coe文件,在通过调用FPGA中的MAC FIR IP Core加载coe文件即可。由于复数乘法存在实部和虚部,复数乘法为
| $(a + b{\rm{j}}) \cdot (c + d{\rm{j}}) = (a \cdot c - b \cdot d) + (c \cdot b + a \cdot d){\rm{j}}$ |
在FPGA中可以调用4个DSP48来完成[11]。对于内插及延时相加实现是将I个信道并行滤波处理的结果并/串转换组合成一路串行数据输出,硬件实现时可以用并/串转换模块代替实现。
3 多通道信道化雷达发射机仿真 3.1 信道化发射机同时发送多个信号仿真常规雷达发射机无法实现同时刻发射多个信号,若要同时发射多个信号就需要几部发射机联合工作,组成发射机机组阵列来达到目的,这样将带来成本提高、系统复杂和可靠性低等问题。而我们通过信道化技术可以解决上述问题,将频带资源“分段化利用”,不同信号占用不同频带,同时,基带处理器实时处理速率要求也不高。因此,在雷达通信一体化平台设计时,我们就可以将雷达信号和通信信号通过信道化技术一同发射出去;而且雷达信号和通信信号使用的电磁波频率不同,雷达的工作频率一般比无线通信要高,所以两者在频谱占用上基本不存在重叠问题[12]。
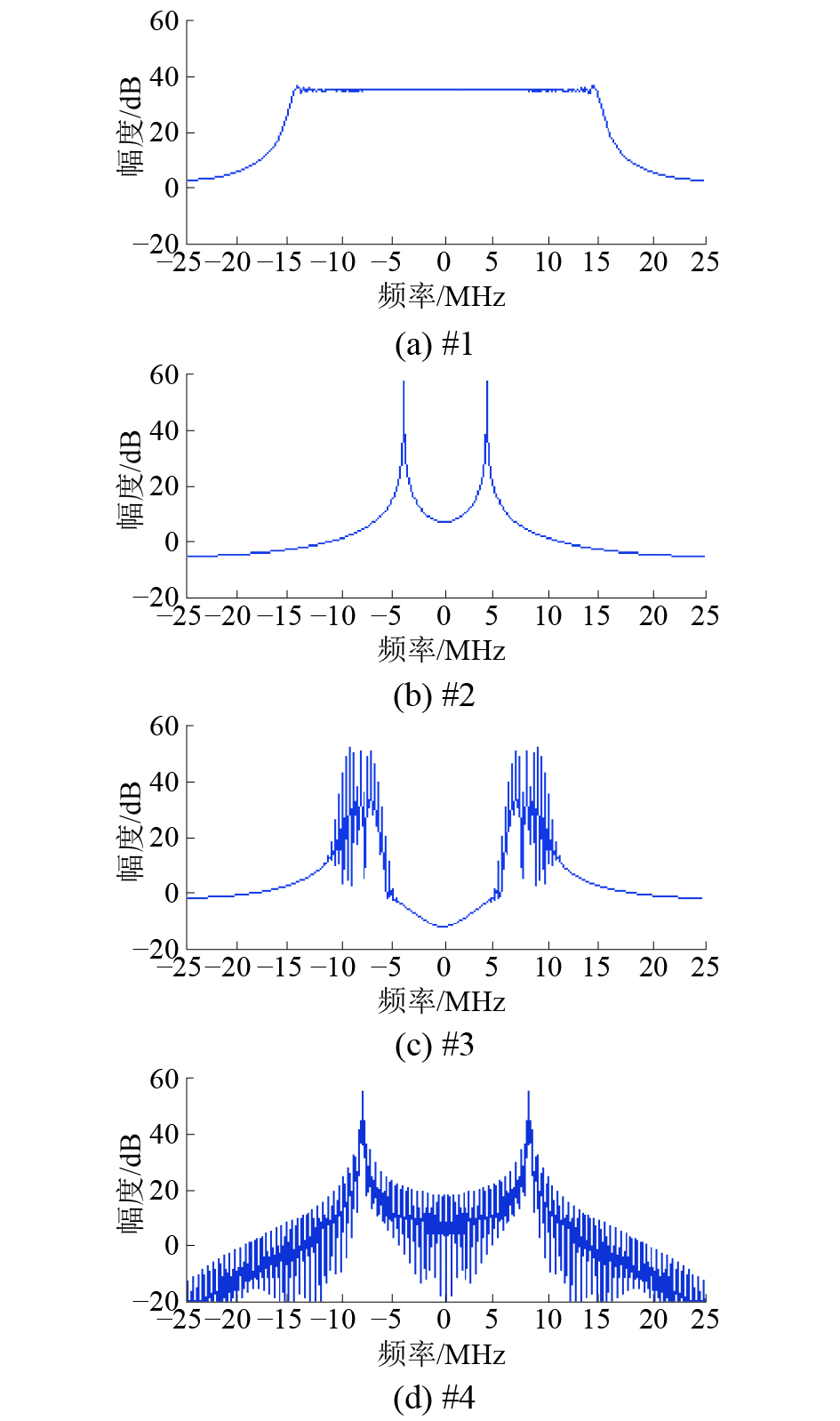
依据图3我们进行了相关计算机仿真,取4路信道,4路信道同时输入发射信号,4路信号采样率都为50 MHz,采样总时长为
|
Download:
|
| 图 6 4路信道输入的发射信号频谱 | |
|
|
表 1 4路信道输入的发射信号仿真参数 |
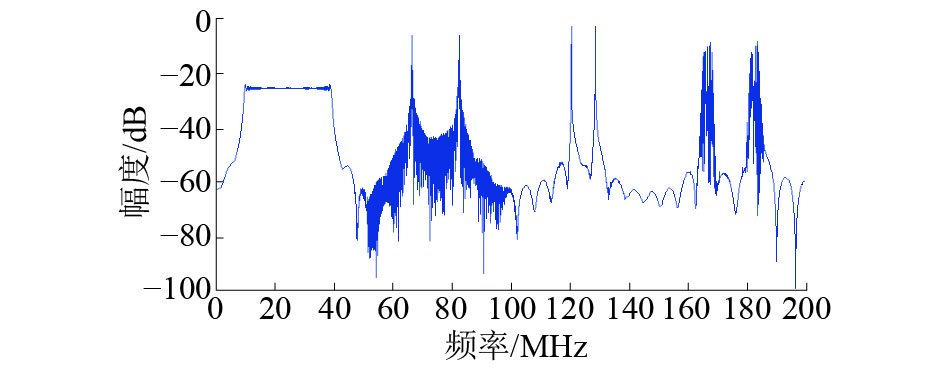
采样频率都为50 MHz,所以最后输出
|
Download:
|
| 图 7 4路信道信道化仿真结果频谱 | |
在大瞬时带宽的雷达发射机系统中,我们经常需要发射一个瞬时带宽很大的雷达信号,而且大带宽的雷达信号一般具有探测精度高、抗干扰能力强,雷达隐蔽性强等优点,适用于穿墙、探底和密集多径场所的高速无线通信等方面[13]。但是往往由于硬件的处理速率不匹配问题而无法产生。为了解决硬件问题,我们可以采用信道化技术合成所需的大带宽雷达信号。在FPGA设计时,可以用其中的直接数字式频率合成器(direct digital synthesizer, DDS)合成个子带信号,通过信道化技术最后输出信号采样率可为FPGA工作频率的数倍,若直接用DDS产生,则存在精度问题和带宽限制问题。
依据图3,我们用MATALAB仿真一个带宽25~175 MHz的线性调频信号。由于需要合成宽带线性调频信号,而实信号
|
|
表 2 4路信道输入的发射信号仿真参数 |
经过信道化结构合成信号的频谱图如图8所示,其中合成的信号带宽大致在25~175 MHz。由图可知在2个信道的交接处会出现断裂现象,这是因为原型滤波器的通带与阻带之间有过渡带,无法实现理想的滤波效果,所以出现这种现象。另外,由于不同信道发射的信号的能量不一样,导致信道化之后的频谱强度不同,会出现频谱幅度不能对齐问题,故需要调整各信道输入信号幅度。

|
Download:
|
| 图 8 4路信道信道化合成线性调频信号仿真 | |
本文主要研究一种基于SDR的可重构多通道雷达发射机。从以上研究可得到如下结论:
1) 本文提出基于SCA架构的SDR通用平台,通过信道化技术实现同时发射多种参数可重构雷达信号功能,具备软硬件可移植、雷达波形和处理算法软件化和系统可升级等优点。
2) 基于多相结构的信道化发射机结构简单、运算效率高、实时处理能力强,解决了硬件速率不匹配的问题,可以广泛应用于大瞬时带宽雷达发射机系统中。
3) 最后仿真结果验证了该多通道雷达发射机系统在同时发射多个信号及发射大宽带信号方面的应用,是该系统模型解决实际问题的理论依据。
4) 该发射机模型如果发射信号的带宽大于设计信道带宽,则存在跨信道问题,该如何解决是下一步研究重点。
| [1] |
汤俊, 吴洪, 魏鲲鹏.. " 软件化雷达”技术研究[J]. 雷达学报, 2015, 4(4): 481-489. ( 0) 0)
|
| [2] |
XU Shaojian, CHEN Bing, ZHANG Ping. Radar-communication integration based on DSSS techniques[C]//Proceedings of the 8th International Conference on Signal Processing. Beijing, China, 2006: 16−20.
( 0) 0)
|
| [3] |
楼才义, 徐建良, 杨小牛. 软件无线电原理与应用[M]. 2版. 北京: 电子工业出版社, 2014: 129−139.
( 0) 0)
|
| [4] |
胡广书. 现代信号处理教程[M]. 2版. 北京: 清华大学出版社, 2015: 131−140.
( 0) 0)
|
| [5] |
邓志民. 多信道软件无线电发射机实现技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2006: 46−51.
( 0) 0)
|
| [6] |
LIU Qing, CAO Kai, LAI Yingyong. FPGA software architecture for software defined radio[J]. Procedia engineering, 2012, 29: 2133-2139. DOI:10.1016/j.proeng.2012.01.275 ( 0) 0)
|
| [7] |
WU Juhong, YANG Dong, CHEN Zengping. Design and application of multi-stage reconfigurable signal processing flow on FPGA[J]. Computers and electrical engineering, 2015, 42: 1-11. DOI:10.1016/j.compeleceng.2014.12.001 ( 0) 0)
|
| [8] |
谭翔. 基于SCA架构的SoPC设计与实现[D]. 长沙: 国防科学技术大学, 2011: 1−8.
( 0) 0)
|
| [9] |
范建华, 王晓波, 李云洲. 基于软件通信体系结构的软件定义无线电系统[J]. 清华大学学报: 自然科学版, 2011, 52(8): 1031-1037. ( 0) 0)
|
| [10] |
许磊, 苏涛. 信道化发射机的FPGA实现[J]. 火控雷达技术, 2010, 39(4): 36-41. ( 0) 0)
|
| [11] |
西瑞克斯(北京)通信设备有限公司. 无线通信中的MATLAB和FPGA实现[M]. 北京: 人民邮电出版社, 2009: 54−78.
( 0) 0)
|
| [12] |
潘玮. LPI雷达信号波形设计与分析[D]. 郑州: 解放军信息工程大学, 2012: 1−15.
( 0) 0)
|
| [13] |
张诚. 宽带复杂雷达信号合成技术研究[D]. 西安: 西安电子科技大学, 2014: 49−51.
( 0) 0)
|
| [14] |
朱华, 黄辉宁, 李永庆, 等. 随机信号分析[M]. 北京: 北京理工大学出版社, 1990: 186−187.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


