在工业和航空航天等领域,亮度测温法、比色测温法、全幅射测温法、电荷耦合元件(charge-coupled device,CCD)测温法以及多光谱辐射测温法等通常是被采用的测温方法,但是测量的往往不是物体表面的真实温度,而是通过物体表面材料的发射率转换成的温度。实验证明,材料发射率不仅与测量目标有关,还与测量环境有关,也就是说辐射测温的适用性受到表面辐射特性和环境因素影响,这使得准确获取物体发射率变得十分困难[1]。在光学辐射测温过程中,发射率的准确性和环境反射是影响温度测量准确性的因素。虽然辐射测温法与热电偶法相比有很多优点,但是在测量温度过程中,周围环境的辐射干扰也成为准确测量温度的主要障碍,特别是对炉和燃烧室的温度测量。在这种情况下,高温计测量的辐射量不仅包括物体表面辐射,还包含很强的环境反射。在测量过程中如果忽视环境因素,其测量结果会偏离真实值。这样相比较之下,利用算法来去除环境反射和未知发射率的影响是一种更加有效的获得真实温度的方法[2]。
多波长辐射测温法是对每一个温度使用多个波长进行测量。在不同的波长下,物体会产生不同的辐射亮度,通过对这些亮度信息数据进行处理,就可以得到物体表面的温度和材料的发射率。这种方法对所测量的物体没有限制,特别适合测量高温物体表面温度。因此,多波长辐射测温可以对高温系统设备的状态进行监测,从而来保障设备的平稳运行[3]。
在多波长测温发展方面,M. Battuello和F. Girard[3]使用多波长高温计测量带有热障涂层的玻璃表面温度和燃烧室气体的温度。ZHENG Jin-Kun等[4]结合使用传统CCD相机、点高温测量计和多光谱成像技术来测量阴极管的温度,通过使用高温计的3个测温点来测量钨阴极温度。XIN Cheng-Yun的研究小组[5]研制了多波段光纤辐射计,对光谱为5~20 μm的灰体进行了温度测量。J. Manara, M等[6]研发了一种彩色CCD相机并提出了三色测温算法来测量粒子表面温度和火焰温度,这种三色测温算法充分支持热电偶测温。在90年代,由哈尔滨工业大学戴景民教授以及他的团队与罗马大学著名的教授G Ruffino合作研制出了35波长高温辐射测温计,成功测得了物体的真实温度,且哈尔滨工业大学等在高温下低发射率材料辐射领域有很高的研究水平。哈尔滨工程大学在国内率先实现涡轮红外温度测量成套装置,且在探头、传感器设计上有较深入的研究[7]。
1 多波长辐射测温原理通常多波长测温以物体的表面温度和辐射强度之间的关系为基础,然而在实际应用中必须涉及到实际物体的发射率。通常实际物体的发射率表现得很复杂,如果用简单的模型描述则会带来很大的计算误差,而用复杂的模型描述不但会增加计算的难度,而且它对光路系统的要求也会变得苛刻[8]。因此考虑到发射率和环境反射的影响,定义物体表面发出辐射强度分布为
| ${I_{{\lambda _i}}} = \varepsilon \left( {{\lambda _i},T} \right){I_b}\left( {{\lambda _i},T} \right)$ | (1) |
式中:T是物体表面温度,
| ${I_b} = {C_1}{\lambda ^{ - 5}}{\left( {{{\rm e}^{{C_2}/\lambda T}} - 1} \right)^{ - 1}}$ |
式中:
物体表面的发射率在窄的波长区域
| ${\varepsilon _i}\left( \lambda \right) = {a_{i,0}} + {a_{i,1}}\lambda , \; \lambda \in \left( {{\lambda _{i,\min }},{\lambda _{i,\max }}} \right) $ | (3) |
式中
每个光谱区域是一个波长范围,其发射率近似为线性的。多波长高温计测量值给出
| $F = {\sum\limits_{i = 1,j = 1}^N {\sum\limits_{{\lambda _j} \in \left( {{\lambda _{i,\min }},{\lambda _{i,\max }}} \right)}^M {\left[ {\left( {{I_{{\lambda _j}, {\rm meas}}} - {\varepsilon _i}\left( {{\lambda _j}} \right){I_{{\lambda _j},b}}} \right)/{I_{{\lambda _j}, {\rm meas}}}} \right]^2} } }$ |
式中
然而,在高温环境中含有其他辐射源,当辐射高温计测量高温表面辐射时,会包括物体表面辐射和周围环境的反射:
| ${I_{\lambda , {\rm eff}}} = \varepsilon {I_{\lambda ,b}} + \rho {I_{\rm envir}}$ | (5) |
式中
在高温物体表面和环境之间的多次反射就会被简化为式(3)中的一个单次反射。从式(3)可知:如果忽略环境因素的影响,由于
| $\begin{split}F = & \sum\limits_{i = 1,j = 1}^N {\sum\limits_{{\lambda _j} \in \left( {{\lambda _{i,\min }},{\lambda _{i,\max }}} \right)}^M {\left[ {\left( {{I_{{\lambda _j}, {\rm eff}. {\rm meas}}} - {\varepsilon _i}\left( {{\lambda _j}} \right){I_{{\lambda _j},b}} - } \right.} \right.} } \\& {\left. {\left. {\left( {1 - {\varepsilon _i}\left( {{\lambda _j}} \right)} \right){I_{\rm envir}}} \right)/{I_{{\lambda _j}, {\rm eff}. {\rm meas}}}} \right]^2}\end{split}$ | (6) |
温度和发射率(T, a1, 0, a1, 1, …, aN, 0, aN, 1)的求解过程由式(4)最小值决定。因此通过式(4),多波长测温系统就可以对带有环境反射和未知发射率的物体表面进行温度测量。
2 改进自适应遗传算法原理 2.1 最小二乘法通常使用最小二乘法来计算误差函数,根据最小二乘法的特性,使所有的真实数值与估计数值的误差平方和最小。如果通过最小二乘法所拟合的曲线能使该误差平方和最小,得到的曲线就是最小二乘法拟合曲线。
2.1.1 算法概述设
| $\varphi \left( x \right) = {c_1}{\varphi _1}\left( x \right) + {c_2}{\varphi _2}\left( x \right) + \cdots + {c_m}{\varphi _m}\left( x \right)\;\;\left( {m < n} \right)$ |
式中:
| $\begin{split}R = & \sum\limits_{i = 1}^n {{{\left( {\varphi \left( {{x_i}} \right) - {y_i}} \right)}^2}} = \\& {\sum\limits_{i = 1}^n {{{\left( {{c_1}{\varphi _1}\left( {{x_i}} \right) + {c_2}{\varphi _2}\left( {{x_i}} \right) + \cdots + {c_m}{\varphi _m}\left( {{x_i}} \right) - {y_i}} \right)}^2}} } \end{split}$ |
达到最小,这就是曲线拟合最小二乘法。要使R达到最小,就要求出
方程个数
| $\left\{ \begin{array}{l}{a_{11}}{c_1} + {a_{12}}{c_2} + \cdots + {a_{1m}}{c_m} = {y_1}\\\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( {n > m} \right)\\{a_{n1}}{c_1} + {a_{n2}}{c_2} + \cdots + {a_{nm}}{c_m} = {y_n}\end{array} \right.$ | (9) |
式中:
| $\left\| {{ A { c} - { y}}} \right\|_2^2 = \sum\limits_{i = 1}^n {{{\left( {{a_{i1}}{c_1} + {a_{i2}}{c_2} + \cdots + {a_{im}}{c_m} - {y_i}} \right)}^2}} $ | (10) |
存在定理:超定方程组存在最小二乘解,且是方程组
| $\left\{ \begin{array}{l}{c_1}{\varphi _1}\left( {{x_1}} \right) + {c_2}{\varphi _2}\left( {{x_1}} \right) + \cdots + {c_m}{\varphi _m}\left( {{x_1}} \right) = {y_1}\\{c_1}{\varphi _1}\left( {{x_2}} \right) + {c_2}{\varphi _2}\left( {{x_2}} \right) + \cdots + {c_m}{\varphi _m}\left( {{x_2}} \right) = {y_2}\\ \quad \quad \quad \quad \quad \quad \cdots \cdots \\{c_1}{\varphi _1}\left( {{x_n}} \right) + {c_2}{\varphi _2}\left( {{x_n}} \right) + \cdots + {c_m}{\varphi _m}\left( {{x_n}} \right) = {y_n}\end{array} \right.$ |
写成简明方程组为
| $\varphi \left( {{x_i}} \right) = {y_i},\;\;i = 1\;,\;2\;, \cdots ,\;n.$ |
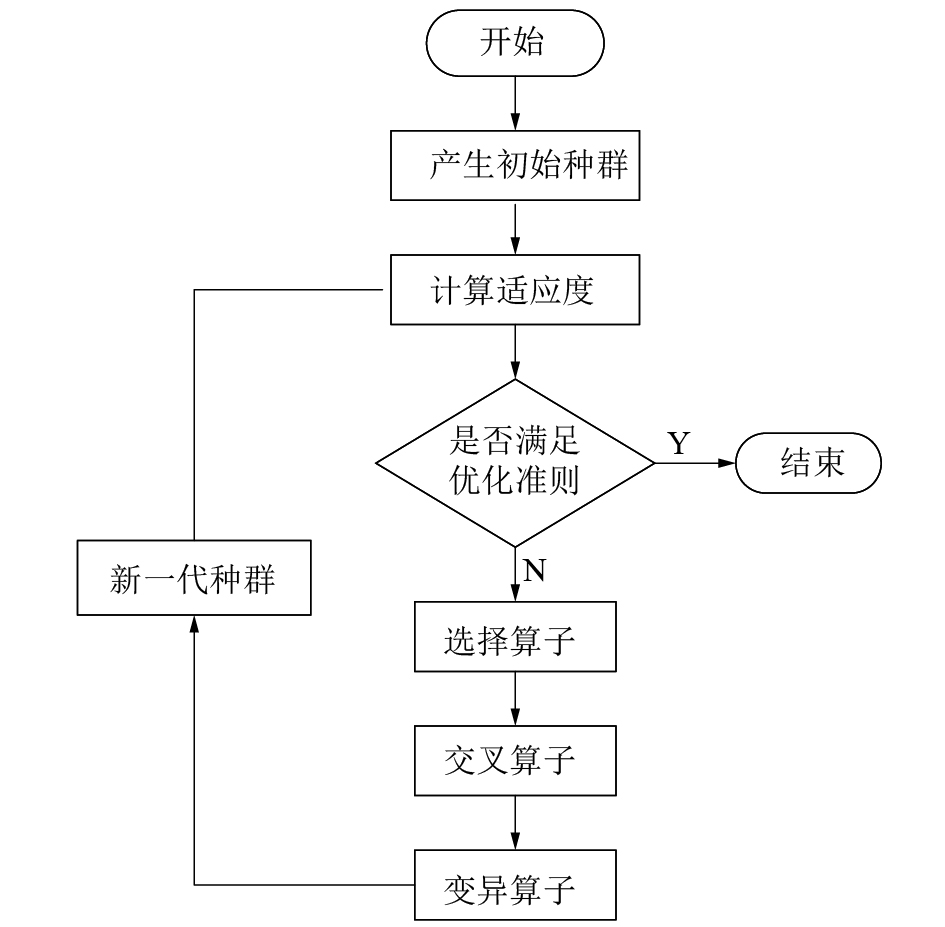
遗传算法(genetic algorithm, GA)是在1975年由美国密执根大学Holland教授首先提出的,Holland教授设计了遗传算法并且对其进行了原理说明。通过统计中的决策理论详细地分析了该算法中的搜索方法,为遗传算法的不断发展提供了理论支持以及坚实的基础。遗传算法的原理实际上是不断进行迭代计算,初始数据随机产生,计算过程模拟进化和遗传过程,在每一次迭代过程中都会产生一组新的解,对于这些解的分析都是通过适应度函数给予评价,遗传算法在计算过程中不断重复,直到满足设定的要求,满足优化准则。图1给出了遗传算法的工作原理流程[9]。
|
Download:
|
| 图 1 GA算法的运算流程 | |
遗传算法由于参数固定,无法满足实际中参数动态和变化的要求,以至于求解的精度不高。从生物进化的角度来说,影响遗传算法性能和效率的根本原因是遗传算法模拟了自然进化过程中后代种群更加适应环境的变化,但却忽略了在种群当中,个体为了增加自身对环境的适应度,其发育及遗传行为也发生了相应的变化。因此,为了避免遗传算法的不足,专家和学者们在遗传算法的基础上提出了自适应遗传算法(adaptive genetic algorithms, AGA)[10]。
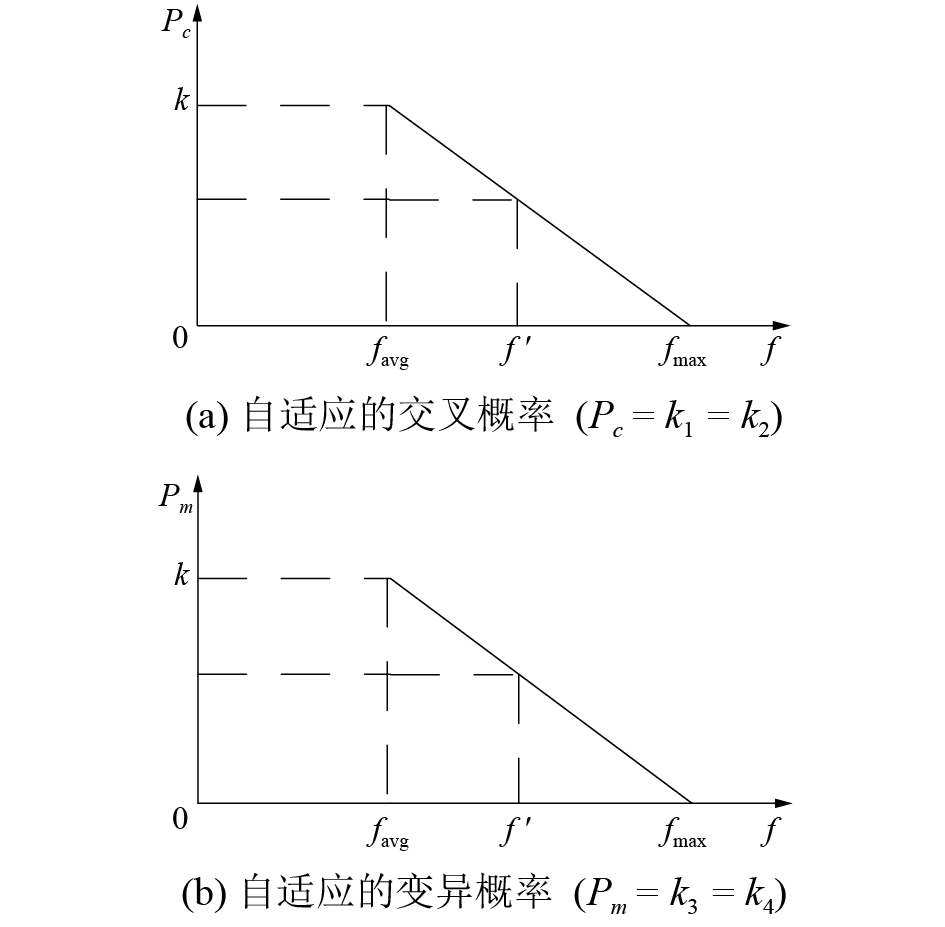
传统的自适应遗传算法于1994年被Srinivas等[11]提出。这种算法的特点是交叉概率
| ${P_c} = \left\{ \begin{aligned}& \frac{{{k_1}\left( {{f_{\max }} - {f'}} \right)}}{{{f_{\max }} - {f_{\rm avg}}}}, \;\;\;{f'} \geqslant {f_{\rm avg}}\\& {k_2}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f'} < {f_{\rm avg}}\end{aligned} \right.$ | (7) |
| ${P_m} = \left\{ \begin{aligned}& \frac{{{k_3}\left( {{f_{\max }} - {f'}} \right)}}{{{f_{\max }} - {f_{\rm avg}}}},\;\;{f'} \geqslant {f_{\rm avg}}\\& {k_4},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f'} < {f_{\rm avg}}\end{aligned} \right.$ | (8) |
式中:
由式(7)、(8)可知:交叉概率
|
Download:
|
| 图 2 AGA算法的交叉概率和变异概率 | |
由图2可知,当适应度低于平均适应度时,可以得出该个体的质量差,需要使用相对来说较大的交叉率和变异率;如果适应度高于平均适应度,可以得出该个体质量好、性能优,则可以取相适应的交叉率和变异率。从图中可以得出,如果适应度越接近最大适应度时,交叉率和变异率的取值就越小;如果适应度等于最大适应度值时,交叉率和变异率的值为零。但是通常这种方法会出现问题,对于遗传算法进化后期比较适合;对于遗传算法进化前期有较大的问题,主要原因是前期进化过程中优秀个体的状态几乎不会发生改变,因此不一定会得到准确的最优解,可能获得的是局部最优解。
传统的自适应遗传算法指出:算法的交叉概率以及变异概率是可以自适应变化的,其变化范围在平均适应度和最大适应度之间,变化的依据是个体的适应度。适应度值与交叉概率和变异概率成反比例关系,适应度值接近于零则可以得到最大的交叉概率和变异概率[12]。这种算法的缺点是:解的求解不一定能跳出局部的范围,尤其是在进化的初期,当演化代数和交叉变异操作不是很彻底时,算法很有可能将局部最优解默认为整个范围内的最优解[13]。
2.4 改进自适应遗传算法通常在传统的遗传算法和现有的遗传算法中,其中的各个参数是已知确定的并且其值不变。为了使遗传算法的性能达到最优,就需要选择合适的参数,如何优化参数就是需要解决的一个重要问题。在自适应遗传算法中,需要对交叉概率和变异概率进行改进,因此本文提出了一种新的自适应遗传算法。
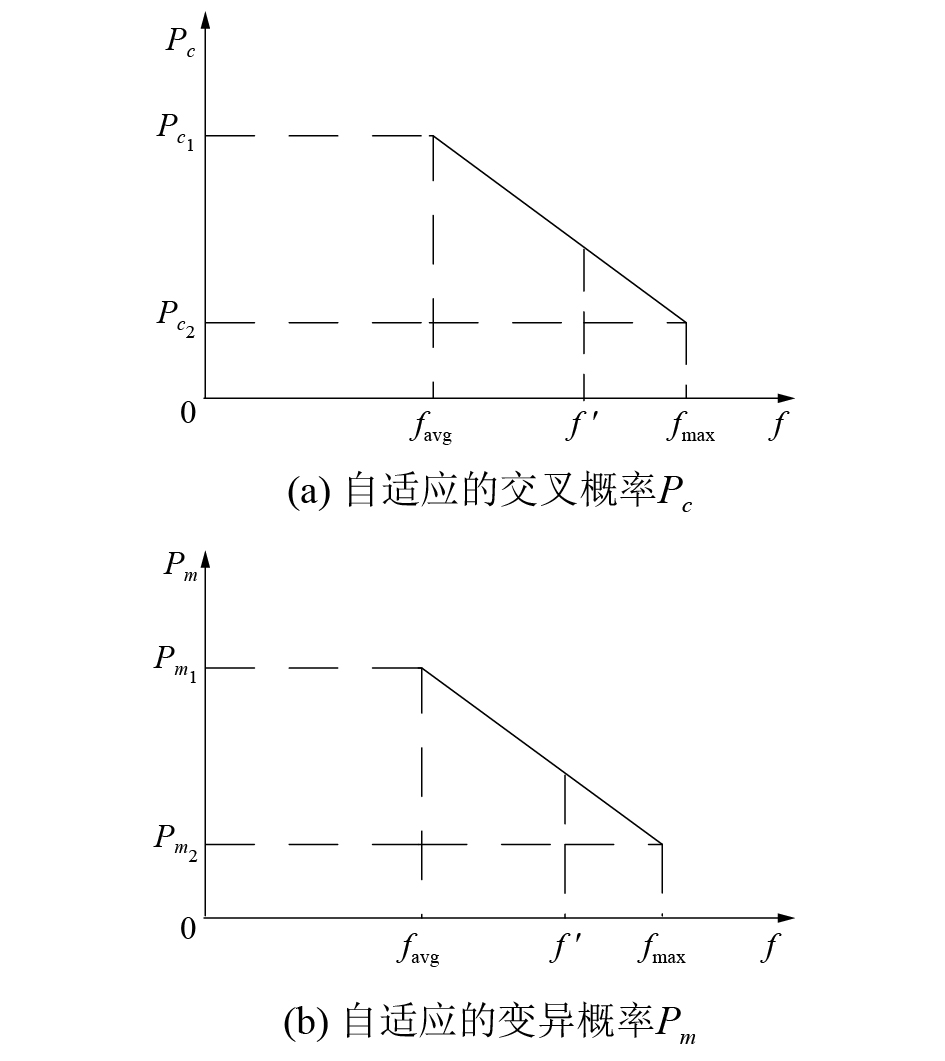
改进的自适应遗传算法(improved adaptive genetic algorithms, IAGA)是在Srinivas等提出的自适应遗传算法的基础上提出的。其交叉概率
| ${P_c} = \left\{ \begin{aligned}& {P_{c_{_1}}} - \frac{{\left( {{P_{{c_{_1}}}} - {P_{{c_{_2}}}}} \right)\left( {{f'} - {f_{\rm avg}}} \right)}}{{{f_{\max }} - {f_{\rm avg}}}},\;\;\;\;\;{f'} \geqslant {f_{\rm avg}}\\& {P_{{c_{_1}}}},\quad \quad \;\;\;\; \quad \quad \quad \quad \quad \quad \quad {f'} < {f_{\rm avg}}\end{aligned} \right.$ | (14) |
| ${P_m} = \left\{ \begin{aligned}& {P_{{m_{_1}}}} - \frac{{\left( {{P_{{m_{_1}}}} - {P_{{m_{_2}}}}} \right)\left( {{f_{\max }} - f} \right)}}{{{f_{\max }} - {f_{\rm avg}}}},\;\;\;f \geqslant {f_{\rm avg}}\\& {P_{{m_{_1}}\;}},\quad \quad \;\; \quad \quad \quad \quad \quad \quad \quad f < {f_{\rm avg}}\end{aligned} \right.$ | (15) |
式中:
由式(9)和(10)可知:改进的自适应遗传算法也可以自适应调整算法的交叉概率和变异概率,与传统的自适应遗传算法比具有相似的变化规律,其调整范围在平均适应度和最大适应度之间,其调整过程依赖于个体的适应度[14]。IAGA算法的交叉概率
|
Download:
|
| 图 3 IAGA算法的交叉概率和变异概率 | |
改进的自适应遗传算法采用了精英保留策略从而保证了每一代的优良个体不被破坏,我们通过用适应度来比较解的好坏。如果当前种群最优个体比下一代种群的最优个体好时,就会将当前种群中的最优个体保留下来,放到下一代中,随机的替代下一代种群中相应数量的个体或替代下一代种群中相应数量的最差个体,从而保证种群的大小一样。精英保留策略保证了当前的最优个体不被遗传操作(交叉、变异等)破坏[15]。改进的自适应遗传算法也存在一定的缺点,容易出现演化停滞不前的现象。当种群中平均适应度值与个体的适应度值大致相等,且平均适应度值接近当代种群中的最大适应度值时,这些个体的模式相当且占据了大部分的种群,此时如果其交叉概率和变异概率也产生了较大的差异,就会使大部分个体的交叉概率和变异概率变得很低,这样就会导致一种恶化现象的产生,即演化停滞不前。这种算法不容易淘汰掉局部的最优个体,从而导致了算法的全局搜索能力不强[16]。
3 仿真过程假设待测物体为热电偶,其温度变化为500~1 000 ℃。当前待测物体的温度为700 ℃,测量过程中选取四路波长为1 000~1 100、1 260~1 450、1 550~1 750、1 850~2 000 nm,所以
本节利用自适应遗传算法来求解被测物体的真温,即用自适应遗传算法求解当误差函数
|
|
表 1 AGA参数设置 |
|
|
表 2 AGA搜索空间 |
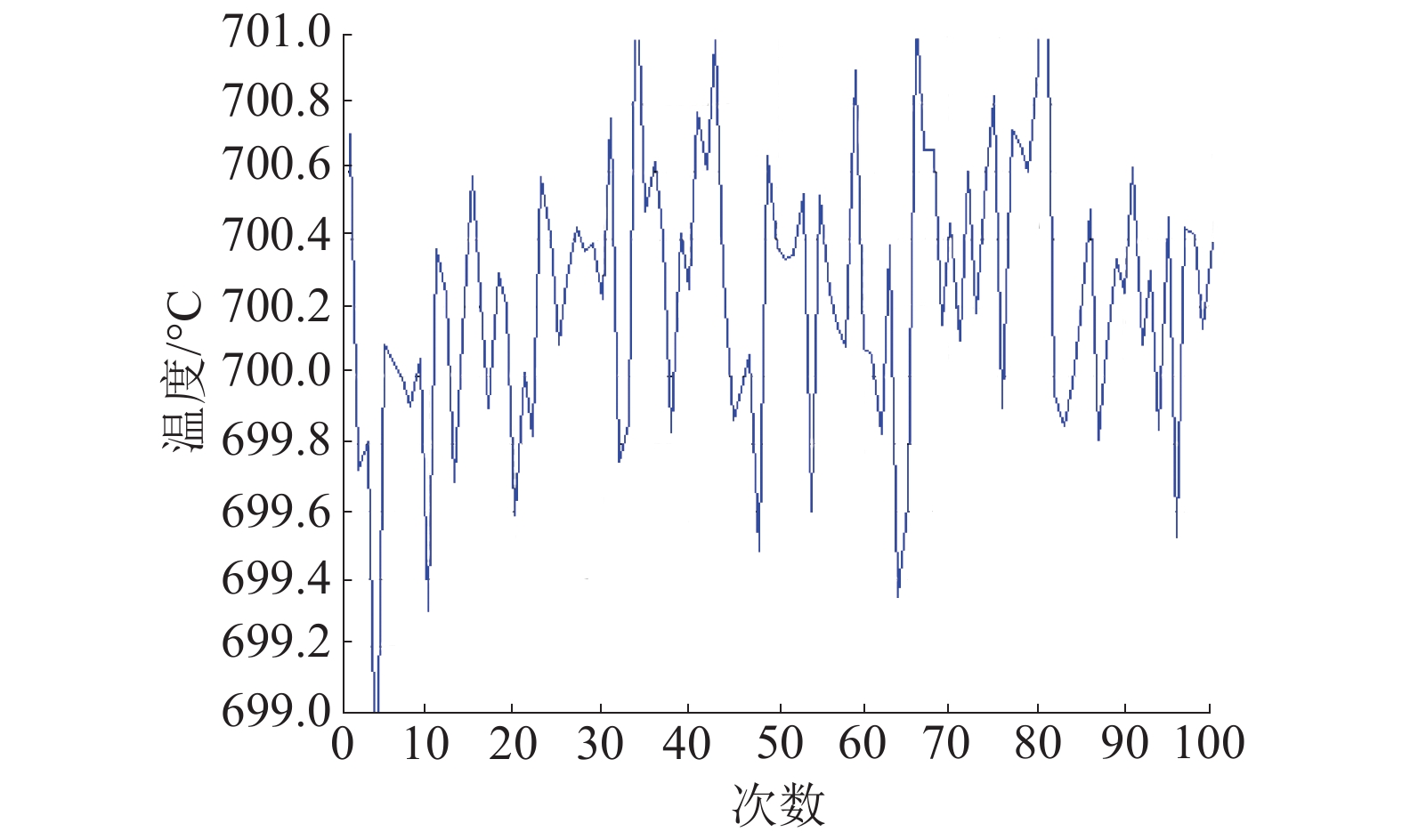
实验过程中利用自适应遗传算法求解温度时,其每次运行的结果都不同,都具有随机性,但是结果都相差很小,所以应该多次计算,从而获得温度的平均值。图4为统计自适应遗传算法计算100次的温度数据,图5为自适应遗传算法计算误差百分比。
|
Download:
|
| 图 4 AGA计算温度(100次结果) | |
|
Download:
|
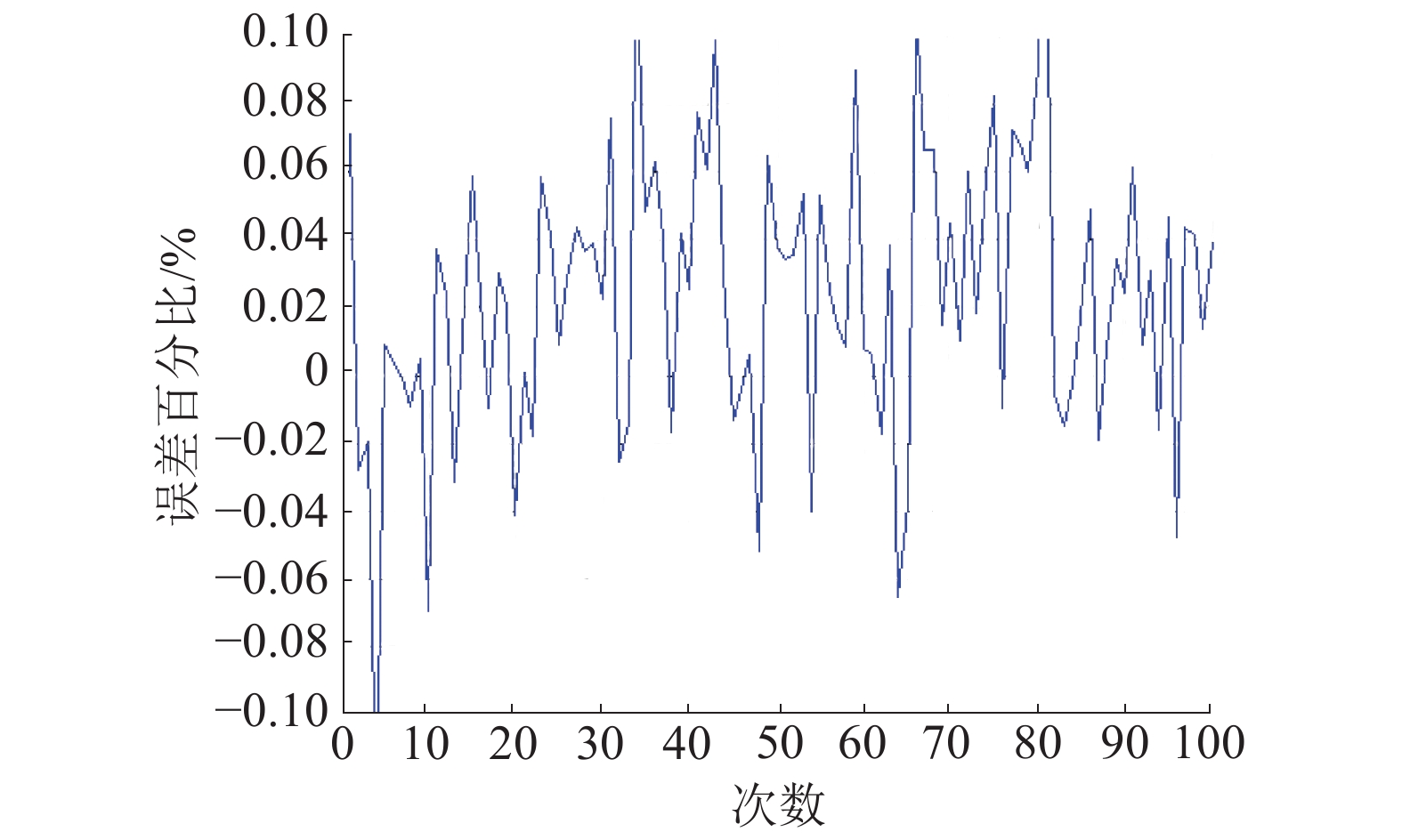
| 图 5 AGA计算误差百分比(100次结果) | |
由图4、5可知,自适应遗传算法计算100次后输出的温度误差范围为-1.27~1.50 ℃,若将100次数据进行平均,则平均温度为700.24 ℃,测温误差为0.24 ℃,误差百分比为0.03%。
3.2 改进的自适应遗传算法仿真结果本节主要是利用改进的自适应遗传算法进行多光谱测温,从而获得被测目标的真温和发射率,即用改进的自适应遗传算法求最优解。
|
|
表 3 IAGA参数设置 |
|
|
表 4 IAGA搜索空间 |
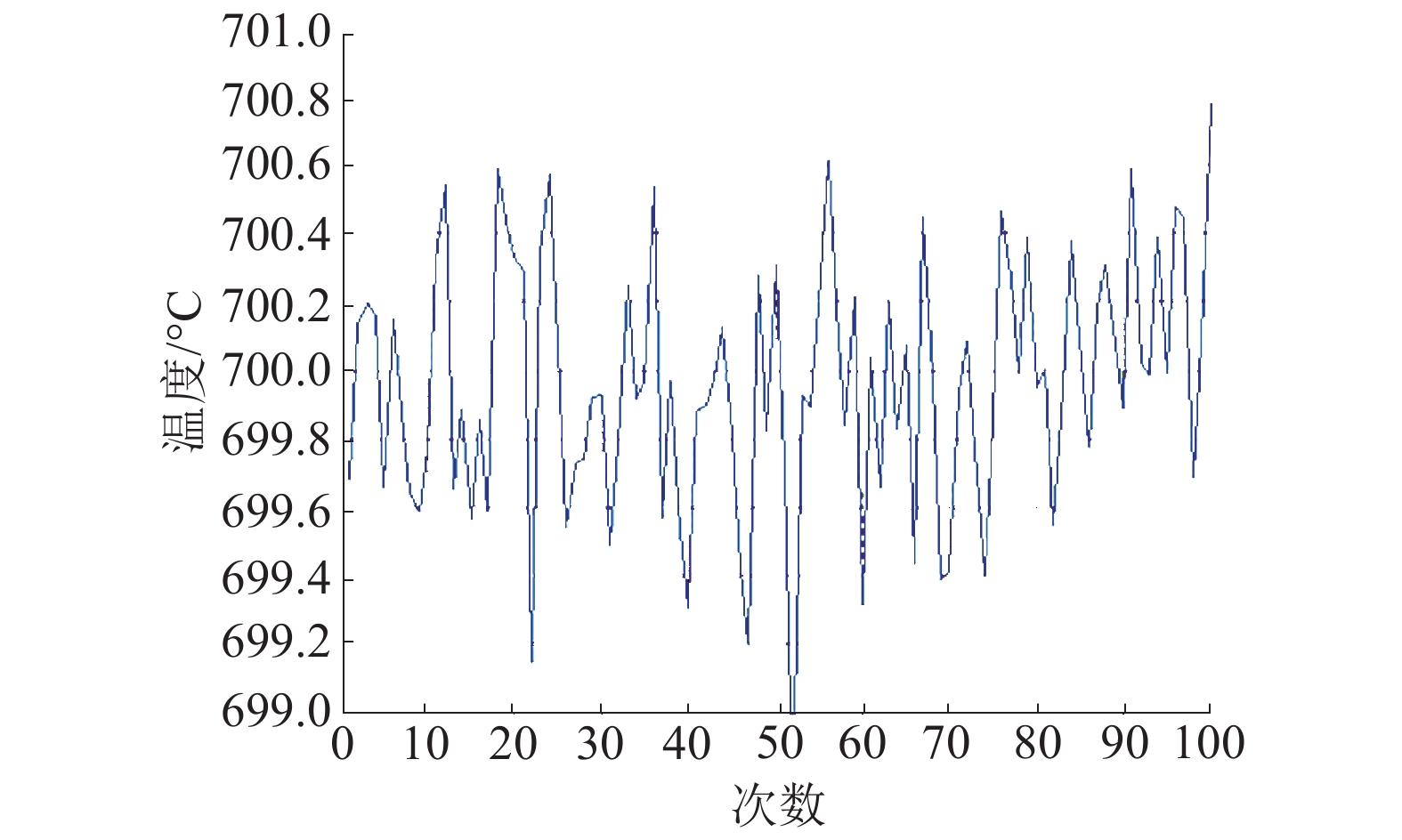
同理,图6为统计改进自适应遗传算法计算100次的温度数据,图7为改进自适应遗传算法计算误差百分比。
|
Download:
|
| 图 6 IAGA计算温度(100次结果) | |

|
Download:
|
| 图 7 IAGA计算误差百分比(100次结果) | |
由图6、7可知,改进的自适应遗传算法计算100次后输出的温度误差为−1.15~0.78 ℃,若将100次数据进行平均,则平均温度为699.95 ℃,测温误差为0.05 ℃,误差百分比为0.007%。
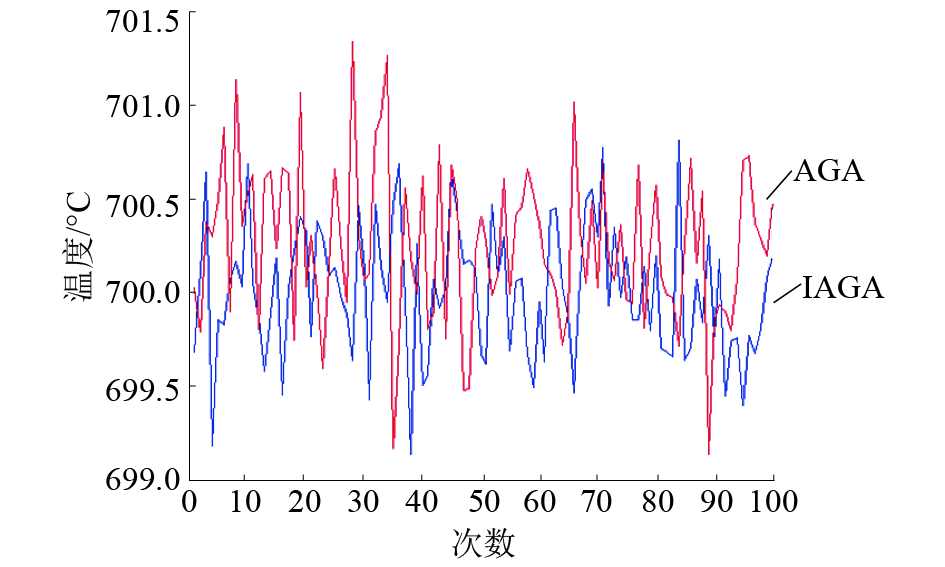
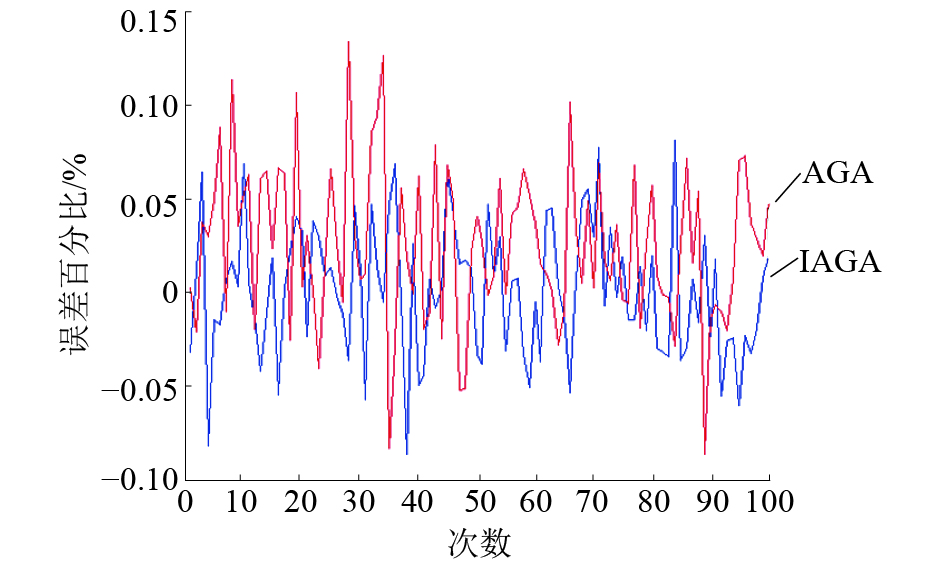
3.3 结果分析自适应遗传算法和改进的自适应遗传算法计算温度和误差百分比的100次结果如图8、9所示。通过图8、9和表5可以看出改进的自适应遗传算法相比于自适应遗传算法具有更高的精度和稳定性。
|
Download:
|
| 图 8 计算温度(100次结果)对比 | |
|
Download:
|
| 图 9 计算误差百分比(100次结果)对比 | |
|
|
表 5 AGA和IAGA对比结果 |
本文利用最小二乘法和改进的自适应遗传算法对四路波长区域对应的辐射数据进行处理,去除环境反射和未知发射率对真实温度的影响。通过划分光谱区域,利用最小二乘法列出误差函数模型,同时比较自适应遗传算法和改进的自适应遗传算法的精确程度,可以得到以下结论。
1) 根据表5实验对比结果来看,采用改进的自适应遗传算法计算的温度更接近于真实温度,误差百分比更低。说明改进的自适应遗传算法具有更好的计算精度。
2) 以热电偶信号为研究对象,通过对实验数据处理及计算结果的分析,进一步验证文中提出的多波长误差函数模型和改进的自适应遗传算法对多波长辐射测温的适用性。
3) 本文研究成果可望应用于工业和航空航天等领域的温度测量。实现一种更加有效的获得真实温度的方法,对高温系统设备的状态进行监测,从而来保障设备的平稳运行。
| [1] |
杨亚斐, 王飞伟, 陈立平, 等. 辐射测温原理及其有效性验证研究[J]. 科技传播, 2016(19): 274-275. ( 0) 0)
|
| [2] |
张文琦. 环境辐射对工业辐射测温影响的研究[D]. 杭州: 中国计量学院, 2015.
( 0) 0)
|
| [3] |
BATTUELLO M, GIRARD F. Characterisation and laboratory investigation of a new ultraviolet multi-wavelength measuring system for high-temperature applications[J]. Measurement, 2016, 87: 126-137. DOI:10.1016/j.measurement.2016.03.024 ( 0) 0)
|
| [4] |
郑锦坤, 白永林, 王博,等. 炸药爆轰瞬时温度的实时测量[J]. 光谱学与光谱分析, 2011, 31(11): 3060-3063. DOI:10.3964/j.issn.1000-0593(2011)11-3060-04 ( 0) 0)
|
| [5] |
辛成运, 程晓舫, 张忠政. 基于光谱响应定标的辐射测温方法[J]. 光谱学与光谱分析, 2012, 32(10): 2735-2738. ( 0) 0)
|
| [6] |
MANARA J, ZIPF M, STARK T, et al. Long wavelength infrared radiation thermometry for non-contact temperature measurements in gas turbines[J]. Infrared physics & technology, 2017, 80: 120-130. ( 0) 0)
|
| [7] |
高山. 燃气轮机叶片温度监测系统设计与实现[D]. 哈尔滨: 哈尔滨工程大学, 2012: 1-10, 20-30.
( 0) 0)
|
| [8] |
肖易寒, 李明逵, 陈立伟. 基于改进NSGA-Ⅱ算法的多光谱测温数据处理[J]. 应用科技, 2017, 44(1): 33-39. ( 0) 0)
|
| [9] |
唐韬. 辐射测温法及其在落管测温中的应用研究[D]. 西安: 西北工业大学, 2005.
( 0) 0)
|
| [10] |
玄光男, 程润伟. 遗传算法与工程优化[M]. 于歆杰, 周根贵, 译. 北京: 清华大学出版社, 2003.
( 0) 0)
|
| [11] |
王亚子. 小生境与并行遗传算法研究[D]. 郑州: 中国人民解放军信息工程大学, 2006.
( 0) 0)
|
| [12] |
王卫荣, 金鹏, 黄康. 免疫遗传算法及其在多目标优化设计中的应用[J]. 机械工程与自动化, 2006(6): 10-12. ( 0) 0)
|
| [13] |
毛丽霞. 基于改进的自适应遗传算法在多目标项目管理中的应用研究[D]. 南昌: 江西理工大学, 2016.
( 0) 0)
|
| [14] |
潘潁. 自适应遗传算法在分布式数据库查询优化中的应用[J]. 内蒙古师范大学学报: 自然科学汉文版, 2016, 45(1): 94-97. ( 0) 0)
|
| [15] |
曲志坚, 张先伟, 曹雁锋, 等. 基于自适应机制的遗传算法研究[J]. 计算机应用研究, 2015, 32(11): 3222-3225, 3229. ( 0) 0)
|
| [16] |
程敏, 宋宇博, 孙刚, 等. 改进的自适应遗传算法及其性能研究[J]. 计算机与数字工程, 2014, 42(3): 355-358, 368. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


