滚筒洗衣机的隔振系统[1]包括弹簧、阻尼和配重,属于多自由度振动系统,决定了整个设备的稳定性、噪声和使用寿命。在连续激励频率下,实验方法很难对隔振系统振动响应[2-3]进行研究。传统的CAE方法基于多刚体动力学理论[4-5],由于钣金件在工作过程中表现出明显的柔性,若不考虑箱体的变形,往往会导致动力学分析结果存在较大误差。为了提高动力学分析结果的可靠性,减小振动响应的幅值,本文提出一种基于虚拟样机的刚柔耦合技术[6]。在充分考虑钣金件变形的前提下,利用ANSYS和ADAMS提升隔振系统的动态响应,并通过LMS进行验证。在灵敏度计算[7]的基础上,应用优化设计理论,得出最佳优化参数(弹簧刚度和阻尼系数)。新的CAE分析与优化方法为运动学和力学研究提供了一定的技术支持,对滚筒洗衣机的设计和开发具有重要意义。
1 耦合分析模型的建立 1.1 隔振系统动力学模型设隔振系统的外部组件总质量为M,弹簧刚度为k,阻尼系数为c,激振质量为m,偏心距为e,激振频率为ω,则该隔振系统的质心在刚性动力学条件下的振幅为:
| $ \begin{array}{l} B = \frac{{me{\omega ^2}}}{k} \cdot \frac{1}{{\sqrt {{{\left( {1 - {\lambda ^2}} \right)}^2} + {{\left( {2\zeta \lambda } \right)}^2}} }} = \\ \;\;\;\;\;\;\;\;\frac{{me}}{M} \cdot \frac{{{\lambda ^2}}}{{\sqrt {{{\left( {1 - {\lambda ^2}} \right)}^2} + {{\left( {2\zeta \lambda } \right)}^2}} }} \end{array} $ | (1) |
式中:λ为系统激振频率与固有频率的比值;参数ζ的计算表达式为
| $ \zeta = \frac{c}{{2M{\omega _n}}} $ | (2) |
影响多自由度隔振系统振动响应特性的关键参数包括弹簧刚度、阻尼系数与配重质量等。但是,当悬挂载体为柔性元件时,外部的变形量对于振幅和激振力的影响不可忽略,只有采用刚柔耦合分析方法才能求解出更加精确的振动响应。
1.2 柔性箱体的定义对于刚柔耦合模型的建立,其关键与核心内容为柔性元件的生成,即柔性箱体的定义,也就是模态中性文件(modal neutral file, MNF)的建立,本文基于ANSYS和ADAMS实现。柔性箱体模型包括质量属性和模态特性[8-9],在动力学分析中能够体现出变形量。在滚筒洗衣机模型中,柔性箱体的定义在有限元分析软件ANSYS中进行,其参数设置如表 1所示,包括两种单元类型:MASS21和SHELL63单元。MASS21类型单元的作用是建立刚性和柔性单元的连接,即通过无穷小的质量单元模拟中继传输节点之间的作用力。SHELL63类型单元具有钣金刚度特性和大变形能力,可承受面内弯曲,用于模拟柔性箱体元件。由于滚筒洗衣机的箱体与弹簧、阻尼器之间的连接点有4个,因此具有4个MASS21单元,由关键点网格划分得到。柔性箱体的结构较为复杂,采用自由网格划分,最终得出网格划分结果如图 1所示。
|
|
表 1 柔性箱体的参数设置 |

|
Download:
|
| 图 1 柔性箱体的网格划分 | |
在软件ANSYS中完成柔性箱体的自由模态分析后,将MNF文件导出。同时,基于软件Mech/Pro将整个隔振系统的三维模型由Pro/E导入ADAMS,得出参数化的刚性动力学仿真模型[10],如图 2所示。通过元件替换的方式,将MNF文件替换掉刚性箱体,得出滚筒洗衣机隔振系统的刚柔耦合模型。为了保证所替换元件的重心一致,需要对坐标系进行对齐处理。

|
Download:
|
| 图 2 刚性隔振系统模型 | |
在模态分析中,系统的动力学方程可以转化为特征值问题:
| $ \left| {\mathit{\boldsymbol{K - }}{\omega ^2}\mathit{\boldsymbol{M}}} \right| = 0 $ | (3) |
式中:M为系统的质量矩阵;K是总的刚度矩阵;ω是自然频率。一般来说,基于有限元法的模态分析中,计算误差将随着模态阶数的增加而增加。因此,仅激活ANSYS计算的前6阶有效固有频率(排除趋于0的固有频率)作为动力学分析的参考,如表 2所示。
|
|
表 2 柔性箱体的前6阶固有频率 |
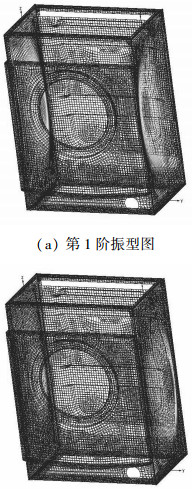
箱体在第1阶和第2阶固有频率下的振型图如图 3所示,可以看出,最大变形位置均在的两侧壁。
|
Download:
|
| 图 3 柔性箱体的典型振型 | |
时域特征主要用于系统动态特性,而非动态响应[11]。为此,文中基于ADAMS/Vibration平台提出隔振系统的频域(频谱)分析[12]。根据洗衣机行业测试要求,将偏心块的质量和偏心距分别在仿真模型中定义为0.3 kg和235 mm。
频谱分析的关键为输入/输出通道的确立。针对滚筒洗衣机隔振系统的结构特点,将激振频率f作为输入通道(0~20 Hz),水平方向位移My、竖直方向位移Mz、弹簧力Fs、阻尼力Fc作为输出通道,可完整地表达出整个刚柔耦合模型的动力学特性。
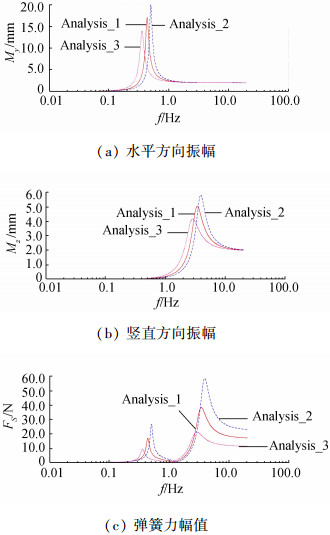
2.2 频谱分析弹簧刚度和阻尼系数是决定隔振系统振动特性的关键参数,其初始值(Analysis_1)分别为7.5 N/mm、0.15 N/(mm·s-1)。为了研究这2种参数对于频谱响应的影响,分别在初始值的+50%(Analysis_2)和-50%(Analysis_3)条件下进行仿真分析,最终得出不同弹簧刚度条件下的频谱曲线如图 3所示,不同阻尼系数条件下的频率曲线如图 4所示。
|
Download:
|
| 图 4 不同弹簧刚度条件下的频谱响应 | |
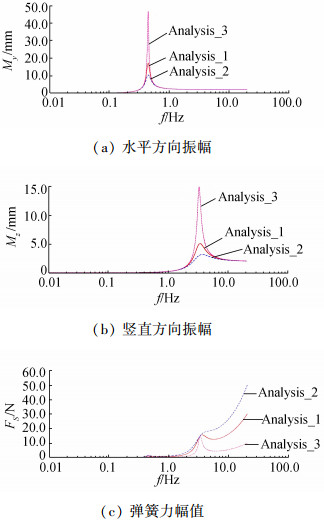
图 4、5中可以看出:随弹簧刚度的增加,隔振系统的共振频率、位移幅值和弹簧力峰值均增大,即在允许承载能力的条件下,弹簧刚度增大时,振动将得到放大;共振点位移幅值随阻尼系数的增加而减小,与阻尼力变化一致,由此可见,如果系统的阻尼系数太小,则不会产生阻尼效应,若阻尼系数过大,整机在地面上的稳定性会降低。
|
Download:
|
| 图 5 不同阻尼系数条件下的频谱响应 | |
为了验证耦合模型的可行性和计算精度,文中基于LMS设备[13]对隔振系统启动阶段的振动位移响应进行实验研究。振动测试的实验安装方案如图 6所示,需要分别在配重顶部安装水平、竖直方向的加速度传感器,从而可通过滤波、积分等方法得出被测点的瞬态位移变化曲线。

|
Download:
|
| 图 6 实验验证方案 | |
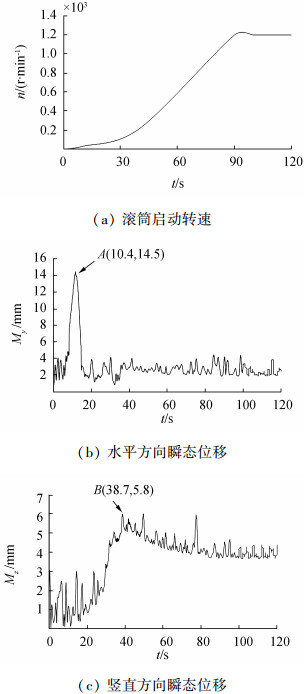
在测试之前,最初的参数定义与设置如下:弹簧刚度为7.5 N/mm,阻尼系数为0.15 N/(mm·s-1),偏心块质量固定在圆筒内壁,大小为0.3 kg。根据电机控制程序和传动比,对内筒转速进行测量和滤波处理,最终得出内筒的启动特性(0~1 200 r/min)如图 7(a)所示。被测点在水平和竖直方向的瞬态位移变化曲线分别如图 7(b)和图 7(c)所示。可以看出:水平方向的最大位移为14.5 mm,表现为图 7(b)中的A点,根据图 6(a)可知,此时对应的转速与图 4(a)中Analysis_1的计算结果一致;竖直方向的最大位移为5.8 mm,表现为图 7(c)中的B点,与图 4(b)中Analysis_1的计算结果一致。由此可见,数值模拟结果具有良好的可行性和较高的计算精度。
|
Download:
|
| 图 7 实验测试结果 | |
灵敏度表现为自变量的梯度变化,反映了性能参数与结构参数之间的潜在关系,利用灵敏度作为评价因子可以明显提高优化效率,在动力模型优化和修改中起着重要作用。从本质上讲,灵敏度是目标函数与优化变量之间的导数。
在优化研究中,灵敏度计算为设计变量的合理取值提供依据,其结果可在ADAMS/insight环境下获得。为了保证灵敏度的全面性,将灵敏度计算的研究水平设定为2个设计变量(弹簧刚度、阻尼系数,浮动范围均为±50%)和4个目标变量(水平方向位移OB_1、竖直方向位移OB_2、弹簧力OB_3、阻尼力OB_4),得出灵敏度计算结果分别如图 8、9所示。

|
Download:
|
| 图 8 弹簧刚度对目标变量的灵敏度 | |
|
Download:
|
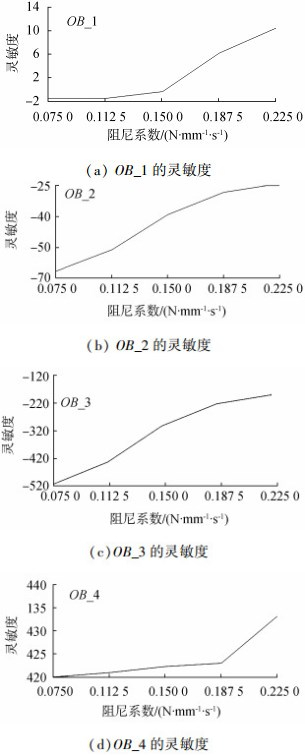
| 图 9 阻尼系数对目标变量的灵敏度 | |
图 8可以看出:弹簧刚度和阻尼系数对于目标变量的影响均较为显著;在弹簧刚度为5.625~9.375 N/mm时,OB_1的灵敏度由负变为正,表明水平方向存在位移的极小值;当弹簧刚度的数值为11.25 N/mm时,OB_2的灵敏度几乎趋于零,表明竖直方向存在位移极小值;弹簧力受弹簧刚度影响较大,阻尼力受弹簧刚度影响较小。
图 9可以看出:阻尼系数对位移的影响更为显著,当阻尼系数的取值在0.112 5~0.15 N/(m·s-1)之间时,水平方向存在最小位移;阻尼系数对弹簧力和阻尼力均有较大的影响,而且作用效果相反。
3.2 优化结果分析在ADAMS/insight环境下,可基于DOE(design of experiment)方法对目标变量进行极值搜索。在多目标变量条件下(同时小于初始值),满足极小值的唯一解是无法得到的,极值搜索得到的是一系列最优解集,也称为pareto解[14-15]。根据灵敏度分析结果设定样本数据的分布,通过软件多次连续迭代计算,得出弹簧刚度和阻尼系数的9种最佳配比,如表 3所示。
|
|
表 3 优化结果 |
多自由度隔振系统具有不确定性,解析法难以求解运动方程,但采用虚拟样机技术可有效地解决这一问题。本文以滚筒洗衣机为研究对象,通过刚柔耦合模型实现了多自由度隔振系统动力学特性的分析有优化,主要得出以下结论:
1) 柔性箱体的最大变形位于两侧壁,可提升侧板钣金刚度的方法提升系统的整体刚度;
2) 采用LMS设备对隔振系统启动阶段的振动位移响应进行实验研究,可有效地验证该耦合模型的可行性和计算精度;
3) 在ADAMS/insight环境下,通过优化计算,可得出设计变量的最佳配比,有效地提升系统的减振效果。
| [1] |
孙玉华, 董大伟, 闫兵, 等. 双层隔振系统有限元建模方法探讨[J]. 机械设计与制造, 2013(1): 244-247. DOI:10.3969/j.issn.1001-3997.2013.01.080 ( 0) 0)
|
| [2] |
曹宏瑞, 李亚敏, 何正嘉, 等. 高速滚动轴承-转子系统时变轴承刚度及振动响应分析[J]. 机械工程学报, 2014, 50(15): 73-81. ( 0) 0)
|
| [3] |
马龙祥, 刘维宁, 李克飞. 移动荷载作用下浮置板轨道振动响应的频域快速数值算法[J]. 铁道学报, 2014, 36(2): 86-94. DOI:10.3969/j.issn.1001-8360.2014.02.014 ( 0) 0)
|
| [4] |
贾凯凯, 梅江平, 刘松涛, 等. 4自由度并联机构刚体动力学模型[J]. 机械工程学报, 2016, 52(13): 10-16. ( 0) 0)
|
| [5] |
赵振峰, 郭顺宏, 张付军, 等. 对置活塞折叠曲柄内燃机刚体动力学特性分析[J]. 内燃机工程, 2015, 36(6): 91-97. ( 0) 0)
|
| [6] |
李欣冉, 陈无畏, 陈晓新. 基于刚柔耦合模型的悬架NVH性能研究[J]. 中国机械工程, 2014, 25(7): 978-983. DOI:10.3969/j.issn.1004-132X.2014.07.023 ( 0) 0)
|
| [7] |
杨冬, 周勤勇, 刘玉田. 基于灵敏度分析的限流方案优化决策方法[J]. 电力自动化设备, 2015, 35(5): 111-118. ( 0) 0)
|
| [8] |
刘宇飞, 辛克贵, 樊健生, 等. 环境激励下结构模态参数识别方法综述[J]. 工程力学, 2014, 31(4): 46-53. ( 0) 0)
|
| [9] |
李发宗, 童水光, 王相兵. 基于模态分析的液压挖掘机工作装置动态优化设计[J]. 农业机械学报, 2014, 45(4): 28-36. ( 0) 0)
|
| [10] |
成伟华. 多刚体动力学仿真技术在汽车设计中的应用[J]. 时代农机, 2016, 43(4): 45-46, 52. DOI:10.3969/j.issn.1007-8320.2016.04.028 ( 0) 0)
|
| [11] |
唐治, 陈慧岩. 自动变速器液压系统动态响应特性试验研究[J]. 液压与气动, 2015(8): 44-46, 72. DOI:10.11832/j.issn.1000-4858.2015.08.009 ( 0) 0)
|
| [12] |
梁西昌, 万熠, 朱振杰, 等. 频谱分析法在振动时效系统中的实验研究[J]. 实验技术与管理, 2015, 32(2): 65-68. DOI:10.3969/j.issn.1002-4956.2015.02.017 ( 0) 0)
|
| [13] |
CARNAHAN J J, RICHARDS C M. A modification to filtered-X LMS control for airfoil vibration and flutter suppression[J]. Journal of vibration and control, 2008, 14(6): 831-848. DOI:10.1177/1077546307084240 ( 0) 0)
|
| [14] |
邢宇飞, 王成恩, 柳强. 基于Pareto解集蚁群算法的拆卸序列规划[J]. 机械工程学报, 2012, 48(9): 186-192. ( 0) 0)
|
| [15] |
DELL'OLMO P, GENTILI M, SCOZZARI A. On finding dissimilar Pareto-optimal paths[J]. European journal of operational research, 2015, 162(1): 70-82. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


