2. 四川大学 计算机学院, 四川 成都 610065
2. College of Computer Science, Sichuan University, Chengdu 610065, China
随着信息化的发展、实名制的大范围应用,身份证的快速识别技术受到越来越多的关注。传统的身份证识别方法主要有2种:一种是通过芯片扫描设备读取身份证内嵌芯片信息,该方法需要专用的芯片识别装置,成本较高,且便携性不足;另一种方法是手动登记,效率低下且容易出错。近几年来,模式识别理论以及图像处理技术的发展为利用光学图像实现证件识别奠定了理论基础,具备拍照功能的智能手机广泛使用为证件识别提供了硬件平台。基于光学摄像头图像处理及模式识别理论的光学字符识别(optical character recognition,OCR)在社会生活的各个行业得到了广泛的使用,如车牌识别、扫码支付等。OCR在文字识别方面具有高速、高效、低成本的优势。
人工神经网络是对动物神经网络的简单模仿,依靠系统的复杂程度,通过调整内部大量节点之间的相互连接关系,从而达到处理信息的目的,被广泛应用于语音分析、图像识别、数字水印、计算机视觉等很多领域,取得了许多突出的成果[1-2]。本文利用深度学习来实现身份证问题图片识别。
1 字符定位与切割在实际应用中,我们可以通过设定拍摄窗口的方式获得身份证的整个版面信息,如图 1(a)是自然拍摄得到的一个身份证图片。为了减少数据的处理量和提取身份证号码区域,将拍摄得到的RGB图片做灰度化处理。Ostu是一种常用的二值化方法,通过统计整个图像的直方图特性来实现全局阈值的自动选取,图像像素能够根据阈值被分成背景和目标2部分。

|
Download:
|
| 图 1 二值化 | |
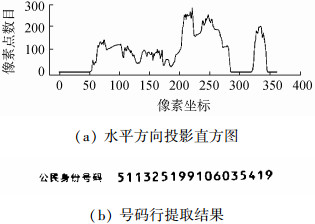
图 1(a)是自然拍摄得到的身份证照片,对其进行ostu运算后得到二值化图像如图 1(b)所示。观察身份证可知号码行与其他信息部分之间有明显的间隔,可以通过对图 1(b)进行投影统计法来提取身份证号码行内容。遍历二值化图片,将其黑色像素点往水平方向投影,统计每一行黑色像素点数目如图 2(a)所示。
|
Download:
|
| 图 2 行切割 | |
观察图 2(a)可知,最右侧的波柱对应着身份证号码行,可以通过设置阈值来实现对号码行的切割,最终切割效果如图 2(b)所示。
同理,将提取到的身份证号码行进行垂直方向的投影,统计每一列黑色像素点的数目,选取合适阈值即可获得每个数字的字符图片。一般而言,投影得到的数字图片高度是一致的,但是宽度并不一致。为了规范神经网络的输入,我们需要对其进行大小归一化。数字图片的宽高比例大概为3:4,所以本文统一将图片归一化为宽15 pix,高20 pix(即15×20)大小。
图片大小归一化的常用方法有双线性插值法、最近邻法、面积插值法等。本文使用线性插值法来归一化图片大小,双线性插值法工作如下:设原图高宽为heightX×widthY,原图像素坐标用(x, y)表示,要变换为高宽heightI×widthJ的目标图,目标图像素坐标用(i, j)表示,变换公式为
| $ y = \frac{{{\rm{width}}Y}}{{{\rm{width}}J}} \times j, x = \frac{{{\rm{height}}\mathit{X}}}{{{\rm{height}}I}} \times i $ | (1) |
对于目标图中的(i, j)点,通过式(1)可以找到在原图中对应的一个点(x, y),取点(x, y)十字方向上的4个点(x-1, y)、(x+1, y)、(x, y-1)和(x, y+1)的像素值来确定目标图中的(i, j)点的像素值。
| $ \begin{array}{l} {\rm{gray}}\left( {i, j} \right) = {\rm{gray}}\left( {x - 1, y} \right) \times {s_1} + {\rm{gray}}\left( {x + 1, y} \right) \times \\ \;\;\;\;\;{s_2} + {\rm{gray}}\left( {x, y - 1} \right) \times {s_3} + {\rm{gray}}\left( {x, y + 1} \right) \times {s_4} \end{array} $ | (2) |
式中si(i=1, 2, 3, 4)表示对应点的对角点与点(x, y)确定的正方形的面积。图像归一化效果如图 3所示。
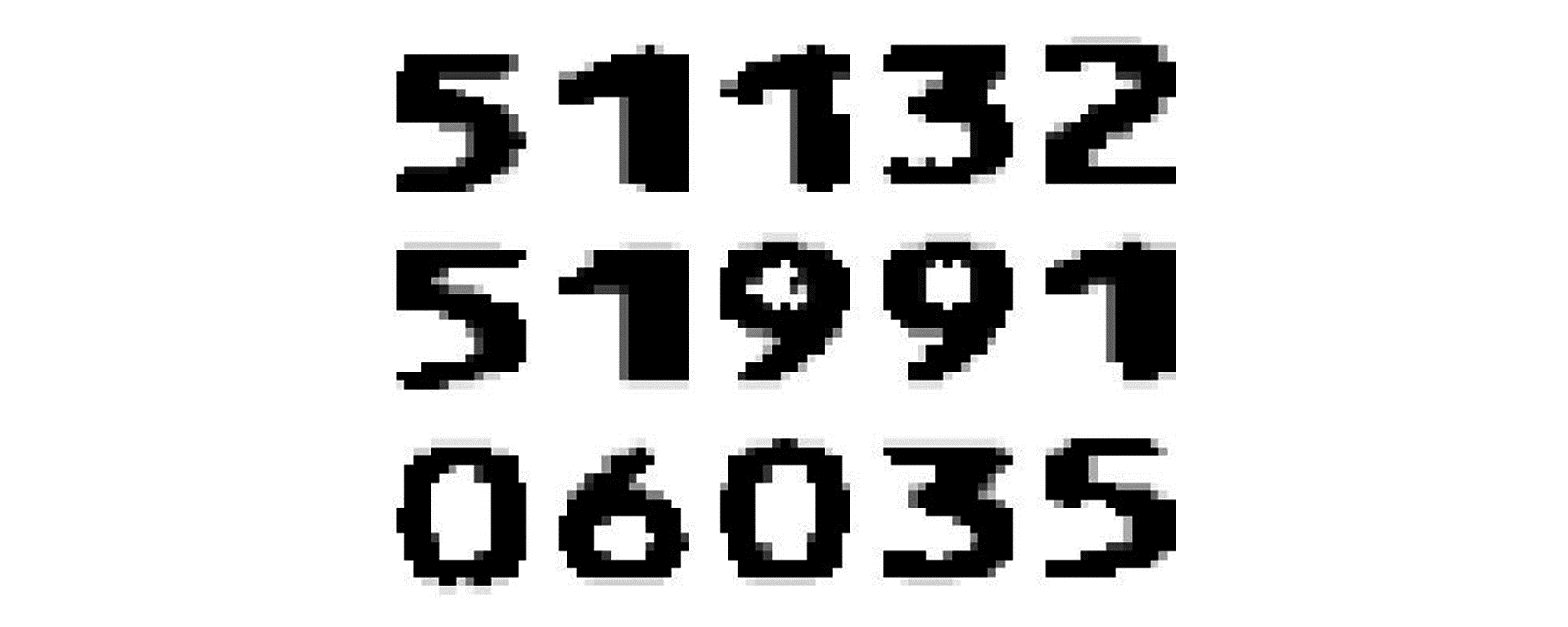
|
Download:
|
| 图 3 字符切割部分结果 | |
深度学习是机器学习的一个分支,它除了可以学习特征和任务之间的关联之外,还能自动从简单特征中提取更复杂的特征。多层神经网络可以解决异或运算。文献[3]已经证明神经网络可以无限逼近任何连续函数。
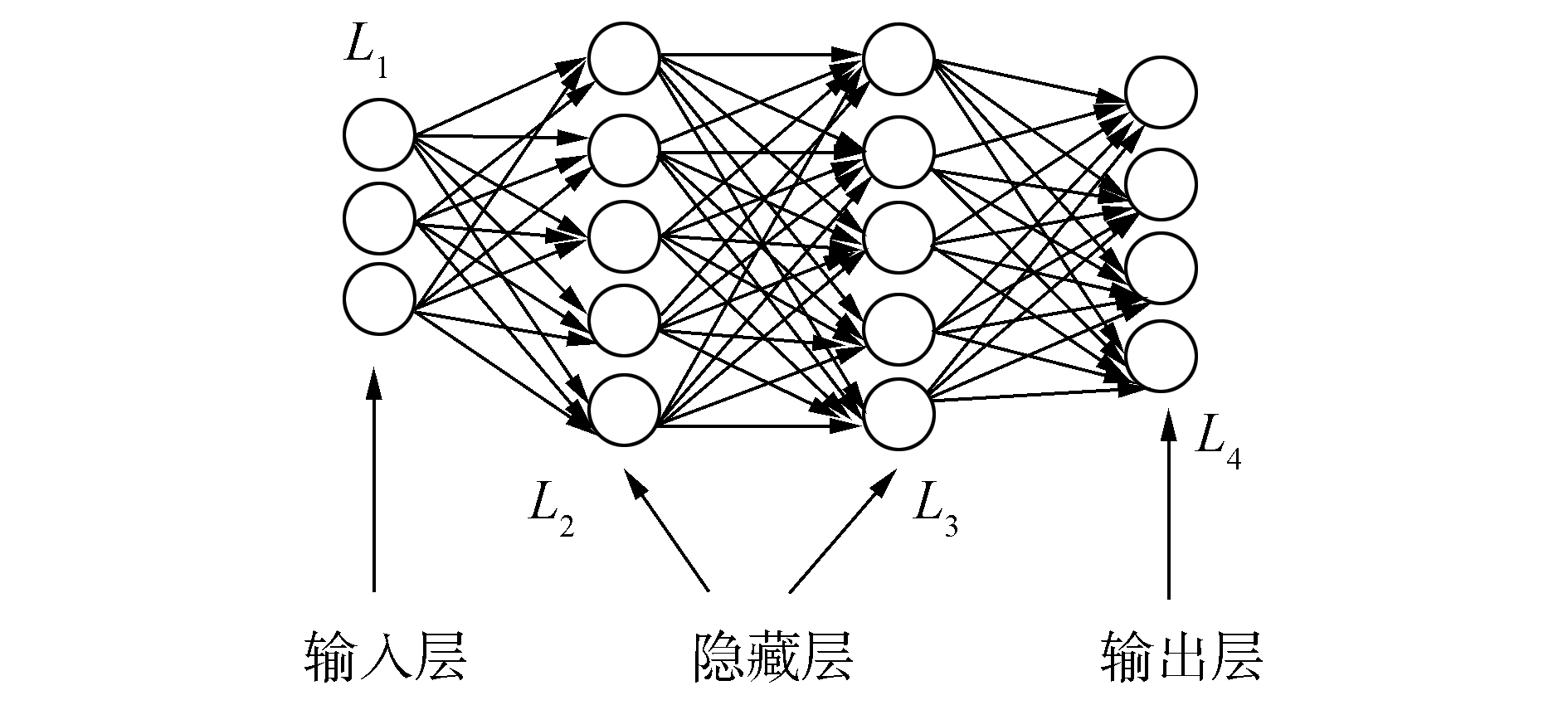
2.1 网络优化策略搭建神经网络一般采用分层结构,输入层作为第一层神经网络,该层的每一个输入神经元对应特征向量中每一个特征的取值,同层节点彼此独立没有任何连接,按照传递方向每层节点只与后一层节点连接直至到输出层。传递是有方向性进行的,传递路径不可逆。在输入层和输出层之间的神经网络叫做隐藏层。网络中所有的神经元具有完全相同的结构。
|
Download:
|
| 图 4 神经网络示意 | |
图片识别问题的本质是图像分类[4-5],分类问题属于监督学习模型,本文涉及的算法也是基于数据驱动型的,在有监督的机器学习中,训练集的选取对网络的性能有着至关重要的影响。神经网络的所有参数都是通过训练集的数据训练得到的,训练集的好坏直接影响了神经网络的性能[6-7]。
本文通过自然拍摄687张身份证图片(包含0~9个数字和英文字符X), 并对其做如第1章的切割处理,得到的像素宽高为15 pix×20 pix的二值化图片共12 366张,将其中8 280张图片作为训练集,其余4 086张图片作为测试机,训练集和测试集图片相互独立、没有重叠。
2.2 网络优化策略结合BP算法和梯度下降法来优化网络中参数的取值。参数调优是使用神经网络时最为关键的步骤之一,优化策略的优劣直接影响了网络最终的识别性能。梯度下降法能将单个参数更新迭代到局部最优值,反向传播算法给出了一个高效的方式能在所有参数上使用梯度下降算法[8]。
用θ表示神经网络中的参数,J(θ)表示在参数为θ时网络模型在训练集上损失函数,则优化过程就是寻找一个参数θ,使得J(θ)最小。
2.2.1 学习率的设置学习率用来控制每次参数更新的幅度,参数更新公式为
| $ {\theta _{n + 1}} = {\theta _n} - \eta \frac{\partial }{{\partial {\theta _n}}}J\left( {{\theta _n}} \right) $ | (3) |
式中η表示学习率。学习率是训练神经网络最重要的超参数,如果η过大,则有可能导致参数在极优值的两侧来回震荡移动,更有甚者会不收敛;如果η过小,虽然保证网络收敛,但牺牲了优化速度。因此η的选取不能过大也不能过小,本文使用指数衰减法来设置学习率:
| $ \eta = {\eta _0}{\alpha ^{k/s}} $ | (4) |
式中:η是每一轮优化时所使用的学习率;η0为事先根据经验设置的初始学习率;α是衰减系数;k为全局训练轮数;s是衰减速度(代表了完整的使用一遍训练数据所需要的迭代轮数)。使用指数衰减法设置学习率,每完整地使过一遍训练数据,学习率就减少一次。通过这种方法,既可以加快训练初期的训练速度,同时在训练后期又不会出现损失函数在极小值周围震荡往返的情况。
2.2.2 过拟合处理神经网络的训练并不是为了追求在训练集上有很好的表现,而是为了在测试未知样例时能有最好的表现。在训练时网络常会发生过拟合现象,通俗来讲就是网络“记住”了训练集中每一个随机噪声而忽略了根据趋势进行合理排除的能力[9-10]。
常用正则化(regularization)来解决网络过拟合问题。正则化的思想是每一个网络参数(权重和偏置)都能对预测产生一点影响,而不是其中几个网络参数起决定作用。具体操作就是在优化时不是直接对J(θ)进行优化,而是对J(θ)+λR(w)进行优化。λ为参数惩罚系数,R(w)表示对网络参数的抑制惩罚。θ为神经网络参数集合(所有权重w和偏置b)。常用的惩罚函数R(w)有2种方式:L1正则化和L2正则化,在本文中使用L2正则化,计算公式为
| $ R\left( w \right) = \left\| w \right\|_2^2 = \sum\limits_i {\left| {w_i^2} \right|} $ | (5) |
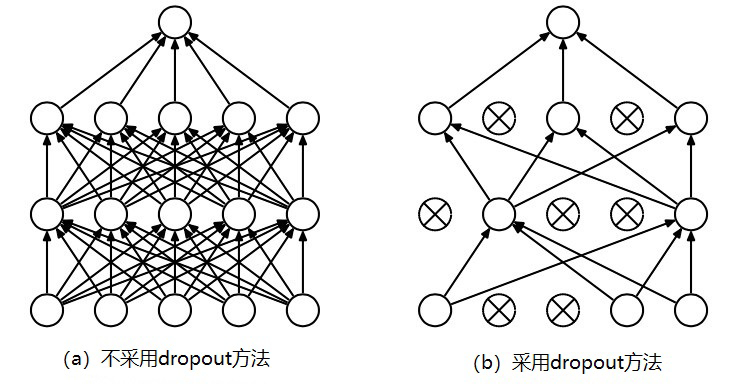
另一种减少过拟合的方式是dropout方法,dropout是一个同正则化完全不同的技术,与L2正则化不同,dropout并不会修改损失函数而是修改神经网络本身。图 5为使用dropout与否的网络训练层间参数传递效果。
|
Download:
|
| 图 5 Dropout示意 | |
通常对于同一批量训练样例,用不同神经元组合训练之后求输出的平均值可以减少过拟合,dropout利用这个原理在训练过程中对网络中的神经元按照一定的概率将其暂时从网络中丢弃,这样就相当于在不同的神经网络上进行训练,减少了层与层之间神经元的依赖性从而使得神经网络更加健壮。
2.2.3 损失函数设计神经网络应用于分类时一般不直接输出结果为哪类,而是输出一个一维数组向量,向量的长度为类别个数。判断每一个样例分类网络就输出一个数组,数组中的每一个元素对应一个类别的得分。如果某个样本属于A类,那么此时网络的输出数组对应于A的元素应该为1,数组其余元素均为0。但是这样的输出在意义上很难直观理解,可以用softmax来优化分类。
神经网络输出为y1, y2, ..., yn,经过softmax函数映射后最终的网络输出为
| $ {{y'}_i} = {\rm{softmax}}{\left( y \right)_i}\frac{{{e^{yi}}}}{{\sum\nolimits_{j = 1}^n {{e^{yi}}} }} $ | (6) |
经过式(6)运算后,神经网络的输出数组变成了一个概率分布。能直观地看到一个样例为各个类别的概率是多大。
采用交叉熵(cross entropy)评判输出向量和期望向量之间的接近程度[11],交叉熵刻画了2个概率分布的距离。给定2个概率分布p和q,通过q来表示p的交叉熵为
| $ H\left( {p, q} \right) = - \sum\limits_x {p\left( x \right)\log q\left( x \right)} $ | (7) |
式(7)的意义是通过概率分布q来表达概率分布p的困难程度。因为希望得到正确的结果,所以选取交叉熵作为神经网络的损失函数时,用p表示样例正确的分类标注,用q表示网络输出的预测值。交叉熵表示p、q越接近(即预测得越准确)。结合式(6)、(7),可以得到神经网络的损失函数为
| $ H\left( {p, {{y'}_i}} \right) = - \sum\limits_x {p\left( x \right)\log {{y'}_i}} $ | (8) |
通过式(8)可以判断预测答案和真实答案之间的距离越小越好。
3 识别实验结果比对为了验证本文算法识别性能,共设计3个实验进行验证。
3.1 基于模版的方法kNN根据我们切割算法及归一化处理可知。切割所得到的字符在15×20大小区域中位置相对固定,可使用模版匹配法来结合kNN算法来进行识别。
kNN算法也叫最近邻法,算法的思想是,每个字符类各取n个有代表性的不同相态字符作为标准模版。待识别图片要进行识别时,将图片与模版里的每一张图片逐个像素点做灰度差值计算,求出2张图片的像素差值绝对之和。在所有模版选取出前k张(本文选取k=5)与待识别图片像素差值绝对值之和最小的图片,统计这k张图片属于哪一个字符类最多的即判断图片为该类,若图片所属类别样例数一样,则选排序在前的类别作为判断类别。如5张图片分别为(1,6,2,3,6),则判断图片为6;若为(2,7,4,X,1),则判断图片为2。表 1为kNN模板匹配法识别结果表。
|
|
表 1 测试集kNN模版匹配法识别结果 |
kNN模版匹配法识别的正确性很大程度上依赖于标准模版的规模。标准模版规模越大,识别正确率越高,但是因为每一次识别时图片都要与模版库里面所有的图片做比较,模版库规模越大,识别所需时间越长。
3.2 全连接网络待识别图片大小为15×20=300个像素点,因此输入层神经元为300个,输出为11类,所以输出层为11个神经元。
搭建一个3层全连接神经网络(输入层+掩藏层+输出层),采用2.2节的优化策略,隐藏层数目与正确率的关系如表 2所示。
|
|
表 2 3层全连接神经网络 |
搭建一个4层全连接神经网络,输入层和2个隐藏层神经元数目相同,每层都为300个,输出层神经元为11个,测试的正确率为99.40%。搭建一个5层的全连接神经网络(每层隐藏层神经元数目与输入层一致),测试集上测试正确率为99.38%,由此可判断多层全连接神经网络与3层全连接神经网络识别性能相当。
3.3 卷积神经网络卷积神经网络是一种深度前馈人工神经网络[12-14]。卷积神经网络特有的卷积层能实现和上一层输入的局部连接,并通过权值共享的方式大大地减少网络的参数量。卷积神经网络架构一般如下:
输入层→(卷积层+→池化层?)+→全连接层+ “卷积层+”表示一层或多层卷积层;“池化层?”表示有或者没有池化层。在经过多轮卷积层和池化层之后,卷积神经网络在输出前一般会经过1~2个全连接层。
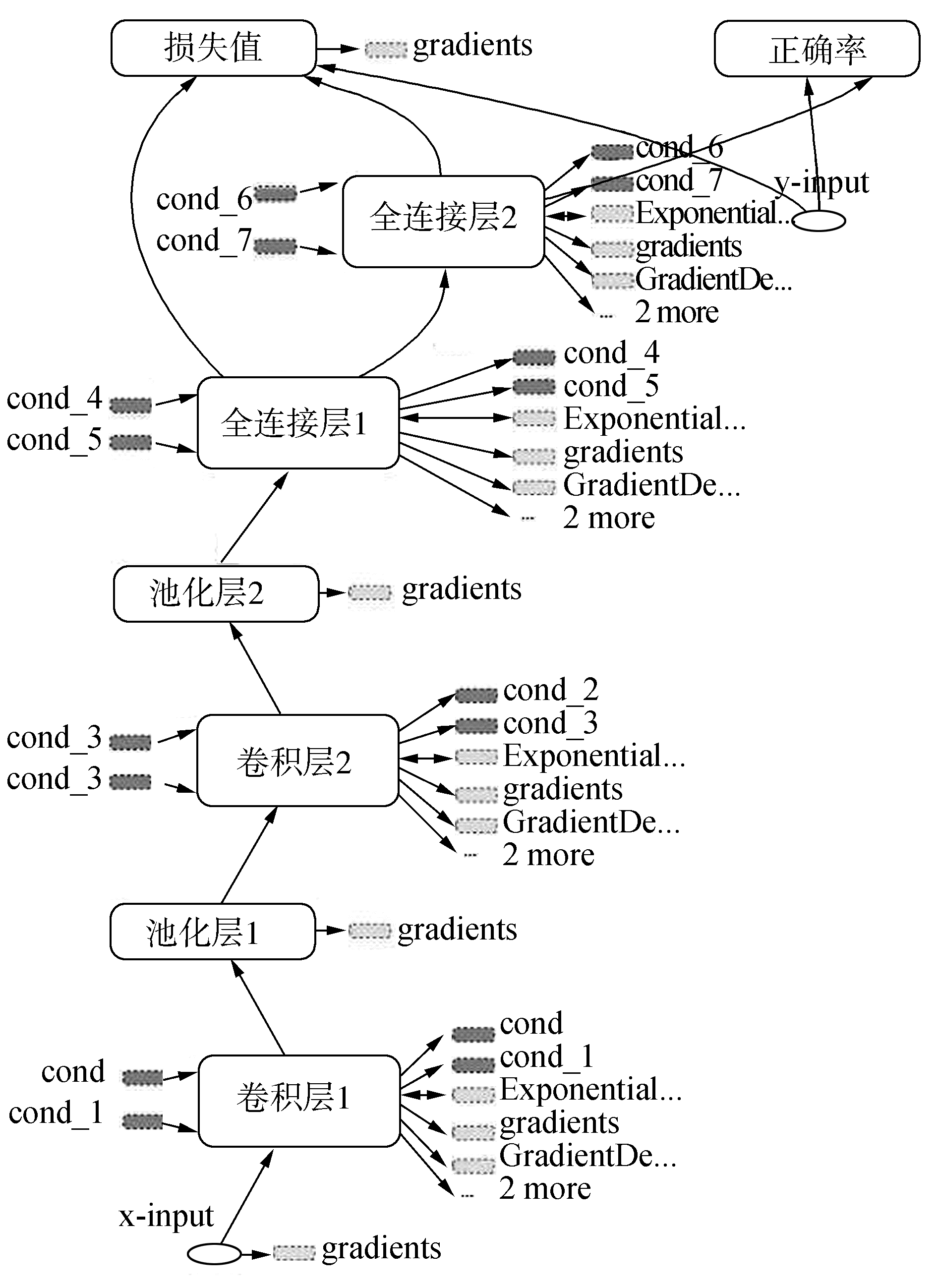
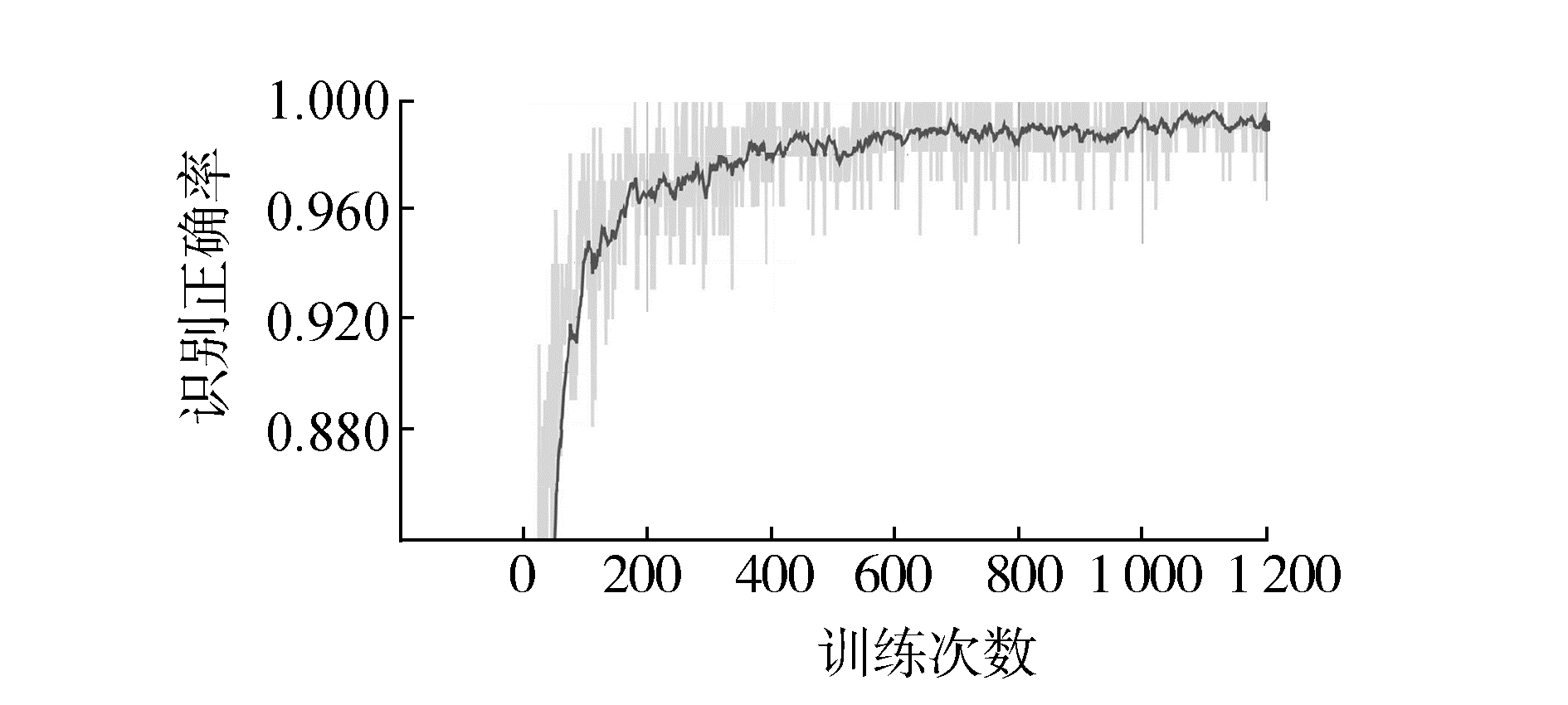
实验所用为7层卷积网络(图 6所示,不含输入层),使用了2个卷积层+池化层组合。第1层卷积层接收的输入层大小为15×20×1的原始文字灰度图片像素,第1个卷积层过滤器的尺寸为5×5,深度为32,使用全0填充,步长为1。第2层池化层,采用最大池化降采样,选择尺寸为2×2的过滤器,使用全0填充且移动步长为2。第3层卷积层,选取边长为5,深度为64的过滤器,移动的步长为1,使用全0填充。第4层池化层结构和第2层池化层结构一致。使用2.1节优化策略训练如图 7。
|
Download:
|
| 图 6 卷积神经网络结构 | |
|
Download:
|
| 图 7 CNN训练过程 | |
经过1 200轮迭代训练,CNN网络在测试集上的识别正确率能达到99.96%。
实验看到BP全连接神经网络和卷积神经网络的识别正确率相近,为了进一步比较2种网络的识别性能,对他们分别初始化训练5次,比较2个网络在5次训练中测试集上的识别正确率如表 3。
|
|
表 3 全连接网络和CNN识别比较 |
不使用优化策略,CNN连续进行5次的识别平均正确率为98.926%;采用优化算法后的网络识别性能提升了0.7%,健壮性更强。由图 6可以看出随着训练次数的增加,网络的模型识别率也在稳步提高,没发生强过拟合现象。
在识别用时上,识别4 086张图片各模型用时如表 4所示。
|
|
表 4 模型识别用时比较 |
图 8是识别时错误识别的样本,左图实际为5,但网络识别为3;右图实际为6,被识别为0。观察图片可以发现,误判很大的原因在于拍摄时曝光不适导致提取字符时噪声过多,致使网络识别错误。

|
Download:
|
| 图 8 部分误识别样例 | |
本文构建了一种基于卷积神经网络的身份证号码分类器。
1) 利用神经网络自动学习的特性避免了传统模式分类算法的复杂特征提取过程;
2) 综合比较了kNN模版匹配法和神经网络识别算法,实验证明使用神经网络识别在识别正确率和识别速度上均优于模板匹配法;
3) 本算法综合采用3种优化神经网络训练的方式来训练网络,识别正确率比不采用优化算法训练提升了0.7%。
下一步的研究方向是要考虑克服拍摄时光照不均匀情况下字符提取和识别问题,并实现身份证汉字部分的高准确率识别。
| [1] |
刘建伟, 刘媛, 罗雄麟. 深度学习研究进展[J]. 计算机应用研究, 2014, 31(7): 1921-1930, 1942. DOI:10.3969/j.issn.1001-3695.2014.07.001 ( 0) 0)
|
| [2] |
郭丽丽, 丁世飞. 深度学习研究进展[J]. 计算机科学, 2015, 42(5): 28-33. ( 0) 0)
|
| [3] |
CYBENKO G. Approximation by superpositions of a sigmoidal function[J]. Approximation theory and its applications, 1993, 9(3): 17-28. ( 0) 0)
|
| [4] |
金连文, 钟卓耀, 杨钊, 等. 深度学习在手写汉字识别中的应用综述[J]. 自动化学报, 2016, 42(8): 1125-1141. ( 0) 0)
|
| [5] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 1026-1034.
( 0) 0)
|
| [6] |
卢宏涛, 张秦川. 深度卷积神经网络在计算机视觉中的应用研究综述[J]. 数据采集与处理, 2016, 31(1): 1-17. ( 0) 0)
|
| [7] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada, 2012: 1097-1105. http://cn.bing.com/academic/profile?id=1dc5d01904d2c274eaec2181a93aa339&encoded=0&v=paper_preview&mkt=zh-cn
( 0) 0)
|
| [8] |
LÉCUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 ( 0) 0)
|
| [9] |
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille, France, 2015: 448-456. http://cn.bing.com/academic/profile?id=fa5b2b149c477985680e5e9cd09f6916&encoded=0&v=paper_preview&mkt=zh-cn
( 0) 0)
|
| [10] |
HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[J]. arXiv:1207.0580, 2012. ( 0) 0)
|
| [11] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 ( 0) 0)
|
| [12] |
胡正平, 陈俊岭, 王蒙, 等. 卷积神经网络分类模型在模式识别中的新进展[J]. 燕山大学学报, 2015, 39(4): 283-291. ( 0) 0)
|
| [13] |
赵志宏, 杨绍普, 马增强. 基于卷积神经网络LeNet-5的车牌字符识别研究[J]. 系统仿真学报, 2010, 22(3): 638-641. ( 0) 0)
|
| [14] |
李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述[J]. 计算机应用, 2016, 36(9): 2508-2515, 2565. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


