2. 林同棪国际工程咨询(中国)有限公司, 重庆 400000
2. T. Y. Lin International Engineering Consulting(China) Co., Ltd., Chongqing 400000, China
地震在短时间内会引起能量巨大的强烈震动, 产生极大的动力效应, 加速钢锚箱的疲劳损伤甚至影响斜拉桥的正常使用性能, 钢锚箱被混凝土包围, 难以检测, 无法准确评估钢锚箱的安全性能[1-3]。众多学者对梁端钢锚箱的疲劳的研究成果较多, 而对索塔端钢锚箱疲劳的研究成果较少。本文以某斜拉桥为工程背景, 分别建立了该桥的整体和细部有限元模型, 选用El-Centro地震波, 分析研究了索塔端钢锚箱的疲劳损伤及震后剩余寿命。
1 疲劳理论结构在发生疲劳破坏时, 应力相对于结构的强度极限非常小, 但在持续的反复荷载作用下, 内部持续发生损伤并不停积累, 最终致使结构毁坏[4]。
本文采用基于S-N曲线的名义应力法[5-7], 按照Palmgren-Miner线性累计原则对结构的疲劳损伤分析评估, 将材料的疲劳损伤按照线性叠加原则分析, 并给出“线性积伤率”公式[6-9], 基本公式如式(1)所示:
| $ D = \sum {D_i} = \sum \frac{{{n_i}}}{{{N_i}}} = \frac{{{n_1}}}{{{N_1}}} + \frac{{{n_2}}}{{{N_2}}} + \frac{{{n_3}}}{{{N_3}}} + ... + \frac{{{n_i}}}{{{N_i}}} $ | (1) |
式中:ni为荷载作用次数, Ni为结构在应力幅Δσi作用下导致疲劳破坏时的应力循环次数, Di为结构在应力幅Δσi作用下的损伤度, D为结构整体损伤程度。
若D≥1, 说明结构已经疲劳破坏; 反之, 说明结构尚未疲劳破坏。将结构受到的各Δσi用一个等效应力幅Δσ0代替, 可表示为
| $ \Delta {\sigma _0} = {\left[{\frac{{\sum {{n_i}} {{(\Delta {\sigma _i})}^m}}}{{\sum {{n_i}} }}} \right]^{\frac{1}{m}}} $ |
对于公路桥梁, 能够引起循环交变应力的因素主要是汽车荷载, 本文将地震作用引起的疲劳损伤折算成同等损伤程度的标准疲劳车当量数。目前我国桥涵通用规范中并无标准疲劳车辆的有关规定, 本文采用的是英国BS5400规范[9-15]。按照泄水法得到构件所经历应力历程的应力幅。
依据Miner理论, 按照线性叠加原理将桥梁在不同载荷车辆作用下产生的疲劳损伤等效为一定值的标准疲劳车荷载, 公式为
| $ {W_e} = {\left[{\sum {{f_i}} W_i^m} \right]^{\frac{1}{m}}} $ |
式中:fi为第i种导致结构疲劳损伤的交通量占总量的百分比, Wi为第i种导致结构疲劳损伤的车辆载重量。
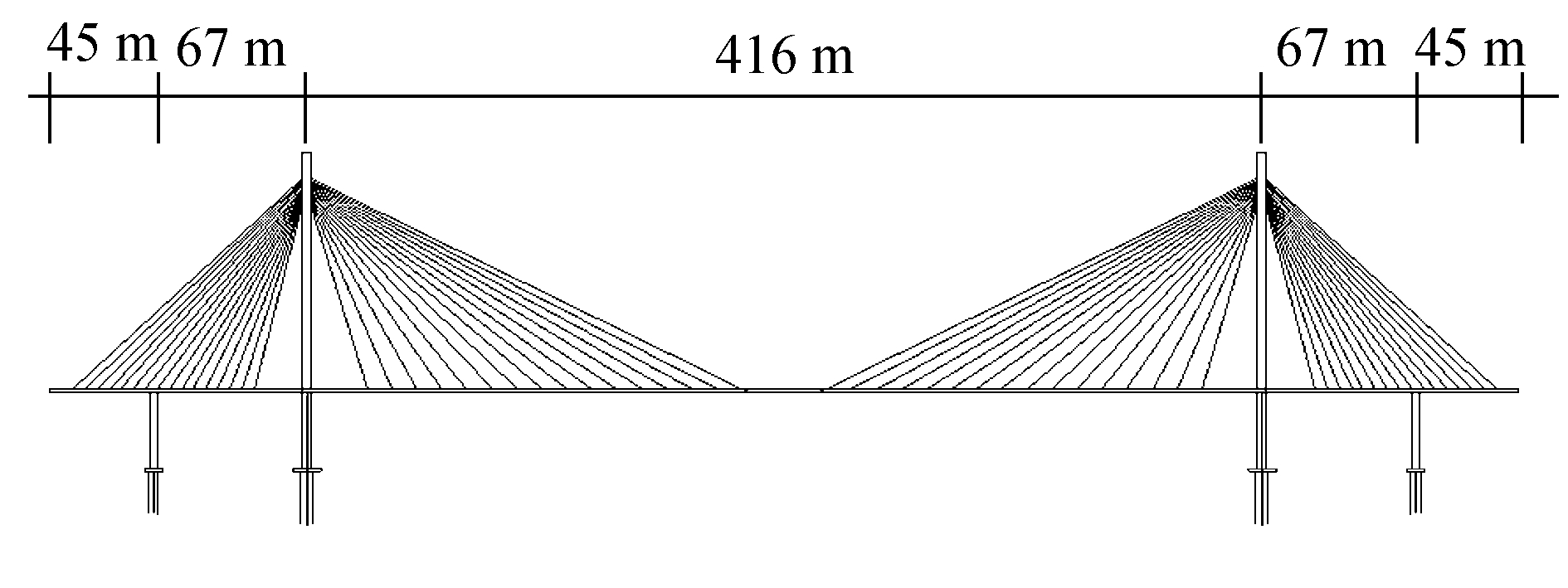
2 依托工程简介本文以双塔双索面钢-砼混合箱梁斜拉桥为工程背景, 跨径为(45+67) m+416 m+(67+45) m, 桥面宽40 m。斜拉索共128根, 锚固在主梁两侧。索塔采用A字型, 索塔钢锚箱采用整体式, 外包混凝土。该桥立面布置如图 1所示。
|
Download:
|
| 图 1 斜拉桥立面布置 | |
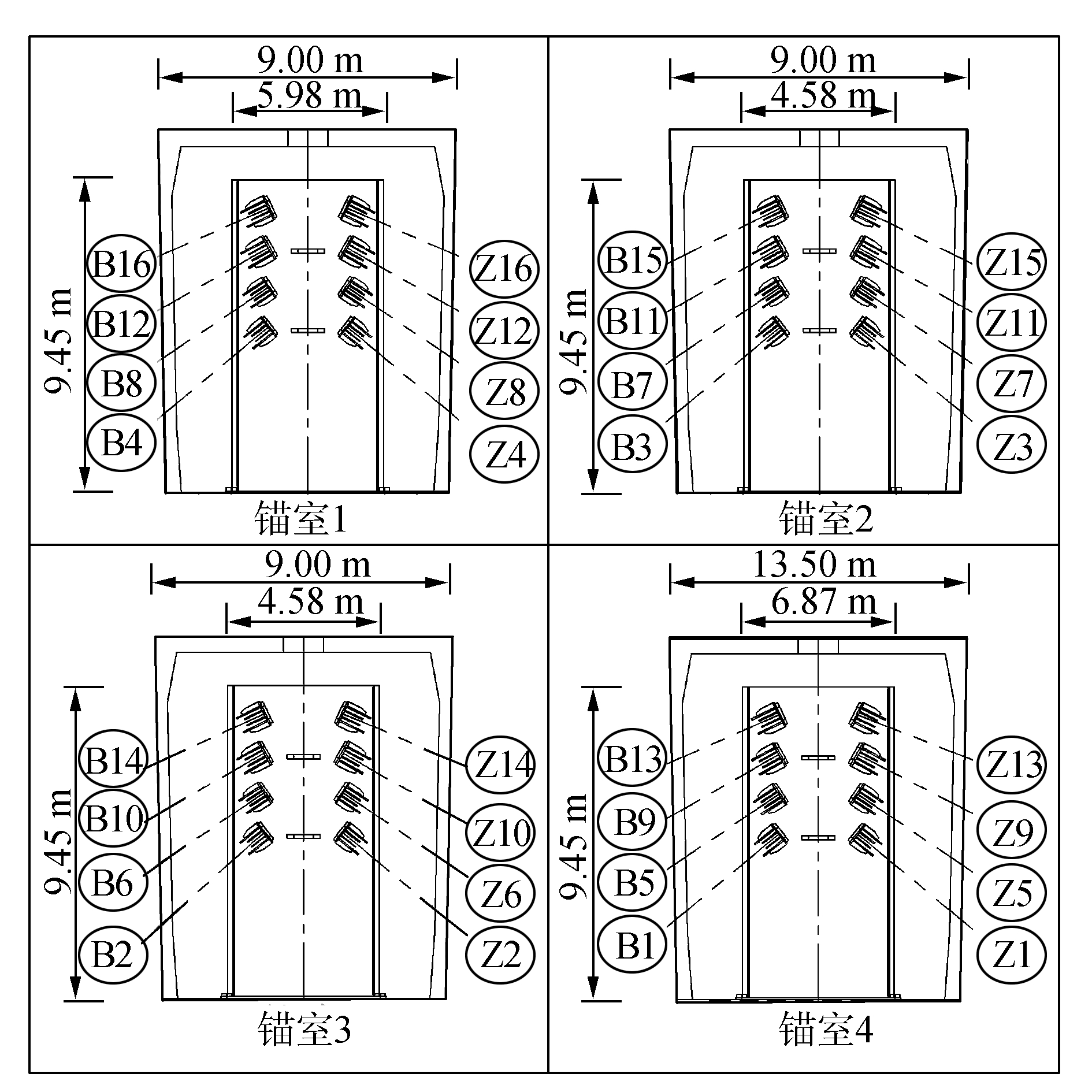
钢锚箱高度9.45 m, 长5.98 m, 宽6.08 m, 共8个锚室。锚室中各板件间焊接, 节段间和腹板间用高强螺栓连接。腹板厚度40 mm, 沿横桥向由内向外编号为F1、F2、F3、F4和F5。钢锚箱结构如图 2~3所示。

|
Download:
|
| 图 2 钢锚箱立面图 | |
|
Download:
|
| 图 3 钢锚箱各锚室立面图 | |
利用Midas/civil建立全桥整体模型, 梁端拉索锚固用刚臂连接模拟, 桥塔处主梁采用的半飘浮体系, 用仅受压弹性连接模拟, 塔底采用固结, 拉索用仅受拉桁架模拟, 如图 4。

|
Download:
|
| 图 4 全桥有限元模型 | |
利用Midas/FEA模拟索塔钢锚箱的细部结构, 该钢锚箱为对称结构, 为了提升计算效率, 取1/2钢锚箱采用板单元建立有限元模型, 并且对锚下肋板等应力集中区域, 细分其单元网格; 对于钢锚箱腹板等应力较小区域, 网格划分较为粗糙, 如图 5。

|
Download:
|
| 图 5 索塔钢锚箱几何模型与有限元模型 | |
构件疲劳破坏一般发生在应力集中区域, 要确定钢锚箱的疲劳破坏点, 应该先找到应力集中点位置。在全桥有限元模型中计算该桥成桥阶段索力, 代入钢锚箱局部模型中计算钢锚箱主应力, 如图 6所示。

|
Download:
|
| 图 6 钢锚箱主应力云图 | |
分析图 6的计算结果, 最终将8个应力集中点确定为疲劳损伤关注点, 对其进行编号, 详见表 3。
|
|
表 3 地震作用下各关注点疲劳损伤程度 |
根据钢锚箱疲劳关注点的构造特征, 参照英国BS5400规范, 将该模型的关注点分为D级和F级, 概率因素d取值为2.0, 各参数取值如表 1。英国BS5400规范提供的S-N设计曲线方程:
| $ \left\{ \begin{array}{l} {\rm{lg}}N = {\rm{lg}}{K_2} + d{\rm{lg}}\Delta-m{\rm{lg}}{\sigma _r}\;(N \le {10^7}, \;{\sigma _r} \ge {\sigma _0})\\ {\rm{lg}}N = {\rm{lg}}{K_2} + d{\rm{lg}}\Delta + 2{\rm{lg}}{\sigma _0}-\left( {m + 2} \right){\rm{lg}}{\sigma _r}(N > {10^7}, \;{\sigma _r} < {\sigma _0}) \end{array} \right. $ | (2) |
|
|
表 1 结构构造分类细节参数表 |
式中:N为按常幅应力加载所预期的致伤次数, K2为统计分析的均值线斜率的倒数, Δ为logN的标准差的反对数的倒数, m为logσr-logN均值线斜率的倒数。
4.3 标准疲劳车作用下钢锚箱关注点的疲劳分析在全桥有限元模型中计算出标准疲劳车加载时的索力-时程曲线, 再根据钢锚箱局部模型计算出各疲劳关注点的应力和等效应力幅值, 根据4.2节计算钢锚箱各疲劳关注点的对数疲劳寿命, 如表 2。
|
|
表 2 标准疲劳车作用下钢锚箱各疲劳关注点的疲劳寿命 |
从表 2可知, 在标准疲劳车作用下, 各疲劳关注点的疲劳寿命均大于7.0, 说明索塔端钢锚箱各疲劳关注点在标准疲劳荷载作用下具有足够的疲劳强度。
4.4 地震作用下索塔钢锚箱疲劳损伤分析地震波不同, 分析结果也会存在一定差异。考虑到钢锚箱的安全性严重影响斜拉桥的安全使用性能, 按最不利原则, 应选取加速度峰值较大、持续时长较长的地震波。通过对迄今记载的强度较大的地震对比分析, 选取El-Centro地震波。
由全桥有限元模型得到的索力时程, 加载到索塔钢锚箱局部有限元模型中, 获得El-Centro地震波作用下各关注点的应力时程, 由于篇幅限制, 仅以关注点A和关注点B为例进行说明, 如图 7。

|
Download:
|
| 图 7 El-Centro地震波作用下的关注点应力时程 | |
根据雨流统计法, 通过MATLAB软件统计分析疲劳关注点的应力时程得到, 关注点应力幅主要为小于10 MPa的低值应力幅, 即减缓了结构发生疲劳破坏的速度。
根据有限元模型分析获得的关注点的应力频谱及式(2)计算出各关注点的疲劳损伤。按照等效原则, 将El-Centro地震作用下各关注点的疲劳损伤折算成同等损伤程度的标准疲劳车数量, 如表 3所示。
从表 3可知, 在一次持续50 s的地震作用下。各疲劳关注点的疲劳损伤均较小, 损伤最严重的是关注点A, 损伤度为9.57×10-6。疲劳关注点的损伤度越大, 折算的等效损伤标准疲劳车数量越小; 损伤度越小, 折算的损伤标准疲劳车数量越大。关注点E和F的折算的标准疲劳车数量远大于其他关注点, 这是因为这2点在标准疲劳车通过一次时的损伤很小, 但地震作用对其造成的疲劳损伤很大, 故同等损伤下折算的标准疲劳车数量较大。
4.5 不同加速度水平地震作用下钢锚箱疲劳损伤分析桥梁运营期间, 可能遇到的地震烈度是未知的, 地震烈度不同, 所引起的疲劳损伤也有所不同。因此, 本文在El-Centro波基础上, 按照0.4、0.5、0.6、0.7、0.8 g共5个加速度水平, 分别计算各疲劳关注点的疲劳损伤度, 分析地震加速度水平对各关注点疲劳损伤的影响。
通过计算不同加速度峰值下各关注点的应力响应可知:随加速度水平的增大, 疲劳关注点的应力循环逐渐从低幅应力向高幅应力发展, 并且高幅应力循环逐渐占据主导地位, 低幅应力循环逐渐消失。
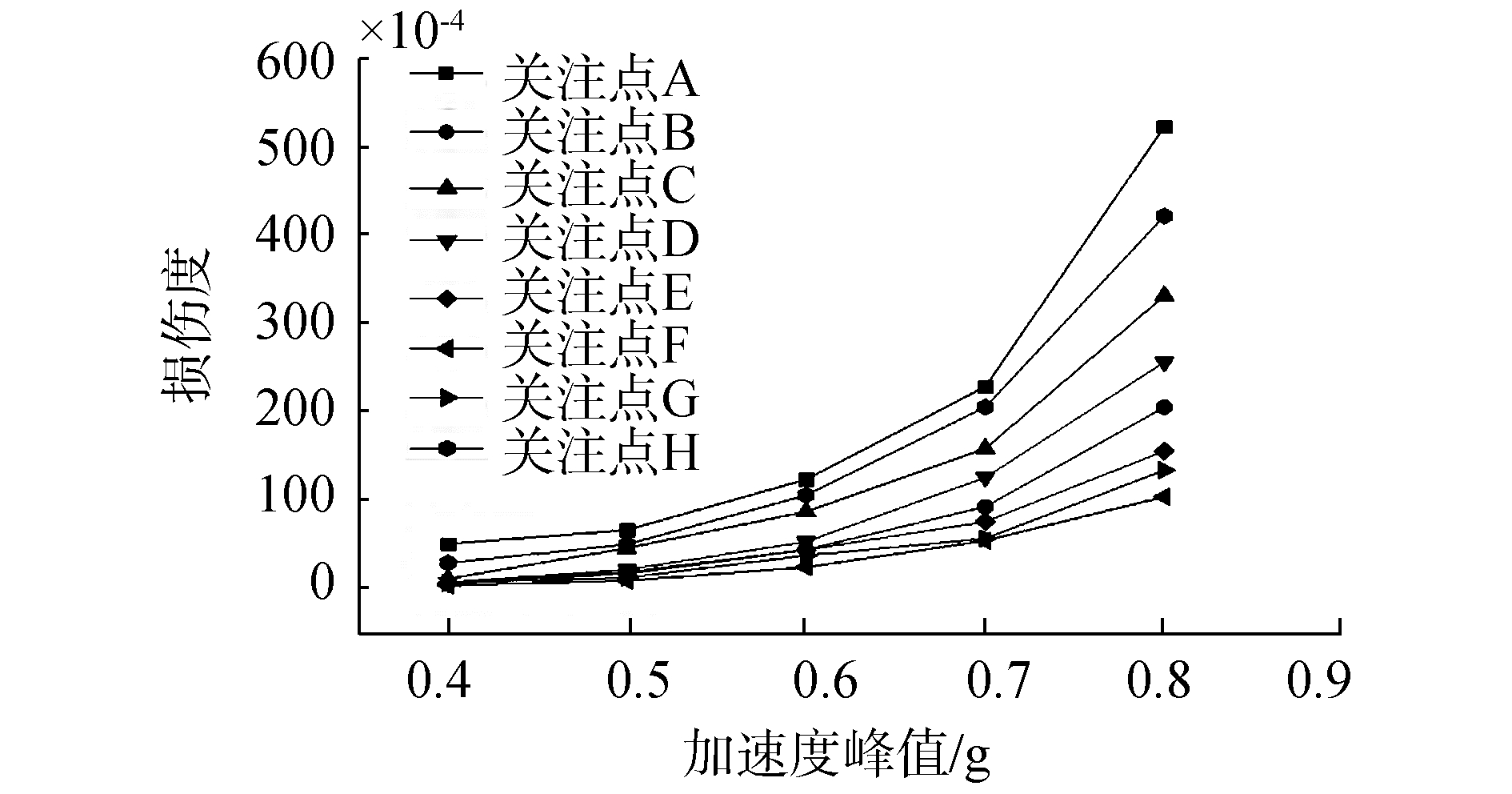
由各加速度峰值水平地震作用下各关注点的应力频谱带入式(2), 得到各加速度峰值水平的地震作用下各注点疲劳损伤并绘制成图, 如图 8, 各关注点同等损伤下折算的标准疲劳车数量如表 4。
|
Download:
|
| 图 8 各关注点疲劳损伤随地震加速度水平变化的趋势图 | |
|
|
表 4 不同加速度峰值水平地震作用下各关注点等效损伤标准疲劳车数量统计表 |
由图 8和表 4中可以看出, 各疲劳关注点的疲劳损伤随加速度峰值水平增加呈非线性趋势变化, 并且各关注点间的损伤度差值逐渐变大, 但各关注点疲劳损伤度排列顺序并不随地震加速度水平的变化而改变。关注点的对数疲劳寿命越大或在地震作用下的疲劳损伤越大, 折算的同等损伤下标准疲劳车辆数就越大。
5 结论本文通过建立了某斜拉桥三维仿真模型, 模拟了该桥及索塔钢锚箱的地震响应, 确定了钢锚箱疲劳关注点位置, 分析了各关注点在El-Centro地震波作用下的疲劳损伤及其随地震加速度峰值水平变化而变化的规律, 得到以下结论:
1) 在El-Centro地震波作用下, 斜拉索索力变化范围很大, 疲劳关注点主要以低值应力循环为主, 有利于减缓材料的疲劳破坏;
2) 在一次持续时间为50 s的El-Centro地震波作用下, 钢锚箱的各疲劳关注点的损伤度整体偏小, 损伤度最大为关注点A, 即B14S索锚块肋板与腹板F3相接处;
3) 地震加速度越大, 疲劳关注点的损伤增长速率越大, 而且损伤最大的均为关注点A, 因此, 关注点A决定钢锚箱的疲劳损伤。
综上所述, 桥梁运营期间若发生地震, 可按照等效原则, 将地震作用下钢锚箱的疲劳损伤换算成同等损伤程度的标准疲劳车数量, 评估震后钢锚箱可持续的剩余通行量, 考虑交通量增长速度, 有助于对桥梁的运营管理, 养护及维修加固。
| [1] |
范立础. 桥梁抗震[M]. 上海: 同济大学出版社, 1996.
( 0) 0)
|
| [2] |
郑史雄, 奚绍中, 杨建忠. 大跨度刚构桥的地震反应分析[J]. 西南交通大学学报, 1997, 32(6): 14-20. ( 0) 0)
|
| [3] |
李默涵. 地震作用下钢管混凝土桩损伤性能研究[D]. 西安: 西安工业大学, 2015.
( 0) 0)
|
| [4] |
周绪红, 吕忠达, 狄谨, 等. 钢箱梁斜拉桥索梁锚固区极限承载力分析[J]. 长安大学学报:自然科学版, 2007, 27(3): 47-51, 56. ( 0) 0)
|
| [5] |
包立新, 卫星, 李俊, 等. 钢箱梁斜拉桥索梁锚固区的抗疲劳性能试验研究[J]. 工程力学, 2007, 24(8): 127-132. DOI:10.3969/j.issn.1000-4750.2007.08.023 ( 0) 0)
|
| [6] |
英国标准学会. BS 5400, 钢桥、混凝土桥及结合桥[S]. 成都: 西南交通大学出版社, 1987: 150-170.
( 0) 0)
|
| [7] |
吴腊梅. 大吨位索力斜拉桥索塔锚固区钢锚箱段力学特性分析[D]. 重庆: 重庆交通大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2567875
( 0) 0)
|
| [8] |
李辉. 斜拉索锚固体系受力性能研究[D]. 天津: 天津大学, 2012.
( 0) 0)
|
| [9] |
高庆峰. 黑瞎子岛乌苏大桥索梁锚固结构静力、疲劳性能研究[D]. 成都: 西南交通大学, 2013. http://industry.wanfangdata.com.cn/dl/Detail/Cstad?id=Cstad_1500130048&type=Free
( 0) 0)
|
| [10] |
徐威. 斜拉桥索塔锚固区节段足尺模型试验及有限元分析[D]. 成都: 西南交通大学, 2007. http://www.cnki.com.cn/Article/CJFDTotal-JCJG201210013.htm
( 0) 0)
|
| [11] |
韦华, 李小刚, 蒋鹰冲, 等. 黄墩大桥索塔锚固区传力途径和受力分析[J]. 城市道桥与防洪, 2009(12): 59-64. DOI:10.3969/j.issn.1009-7716.2009.12.014 ( 0) 0)
|
| [12] |
单炜, 李玉顺, 于玲, 等. 异形截面斜拉桥索塔锚固区节段足尺模型试验研究[J]. 中国公路学报, 2005, 18(3): 60-65. DOI:10.3321/j.issn:1001-7372.2005.03.012 ( 0) 0)
|
| [13] |
苗闫闫, 郝志刚, 任晓崧, 等. 车辆荷载因素对公路钢桥疲劳可靠度的影响[C]//第17届全国结构工程学术会议论文集. 武汉, 中国, 2008: 499-504.
( 0) 0)
|
| [14] |
邵雨虹. 大跨径桥梁疲劳设计车辆荷载谱研究[D]. 西安: 长安大学, 2012.
( 0) 0)
|
| [15] |
任伟平. 焊接钢桥结构细节疲劳行为分析及寿命评估[D]. 成都: 西南交通大学, 2008. https://www.wenkuxiazai.com/doc/6f48c813f18583d049645984.html
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


