大规模MIMO（massive MIMO）技术是新一代增强型MIMO技术，由于它能够极大地提高系统的频谱效率、能量效率和鲁棒性，吸引了很多学者的关注。Massive MIMO技术是最有潜力的第五代通信网络（5G）的关键技术之一^[1-2]。为了设计和评估Massive MIMO系统，建立能够有效展现Massive MIMO信道特征的信道模型至关重要。在一个Massive MIMO系统中，通常在基站端使用可单独控制的数十甚至数百个天线，MIMO信道沿大规模天线阵列轴呈现非平稳特性^[3-4]，即在Massive MIMO系统中任意一个散射簇都不能影响到大规模天线阵列中所有天线，天线阵列轴的每一天线阵元都拥有自己的一组影响其信号传播的散射簇。

Kronecker信道模型是最为广泛使用的信道模型之一，由于该模型复杂度较低且实现简单，常用于研究具有空间相关性的MIMO系统容量和性能仿真分析^[5-6]。为了更好地描述3D信道传播特性，近来有学者提出了一种3D MIMO Kronecker信道模型用于任意结构天线阵列的3D MIMO信道容量和天线间相关性的分析研究^[7]，但该Kronecker模型缺乏对Massive MIMO信道非平稳特性的描述，适用于Massive MIMO系统的3D Kronecker模型还需要进一步研究。

本文提出了一种3D Massive MIMO Kronecker信道模型，采用生灭过程建模散射簇沿阵列轴的非平稳演变^[8-9]，在所提的Kronecker信道模型对信道相关矩阵计算中引入幸存概率矩阵来体现生灭过程的影响，最后通过仿真验证了所提模型不仅可以表征天线相关性，而且可以描述散射簇在大规模天线阵列轴上的演变。

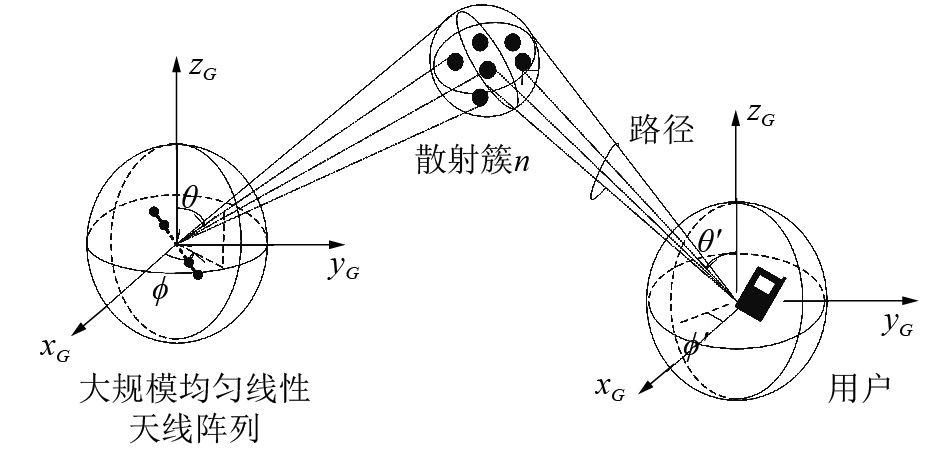
1 3D MIMO Kronecker信道建模 1.1 3D MIMO信道模型

3D MIMO信道模型中散射传输路径可以抽象为散射簇，由方位角、俯仰角和散射簇功率表示，如图1所示。

在图1中，信号以一定的角度从基站发出，经过多个3D散射簇反射后以不同的路径到达用户终端。角度 $\phi $ 和 $\theta $ 分别表示信号经散射簇的水平离开角和仰角离开角， $\phi '$ 和 $\theta '$ 分别代表信号的水平到达角和俯仰到达角。变量 $n$ 代表第 $n$ 个散射簇， $m$ 表示散射簇 $n$ 内的第 $m$ 条散射路径。基站的第 $s$ 根天线和用户的第 $u$ 根天线之间历经散射簇 $n$ 的信道系数为^[10]

$\begin{array}{l}{h_{u,s,n}}(t) = \sqrt {{{{P_n}} / M}} {\sum\limits_{m = 1}^M {\left[ {\begin{array}{*{20}{c}}{{F_{{\rm{RX}},u,\theta '}}\left( {\theta ',\phi '} \right)}\\{{F_{{\rm{RX}},u,\phi '}}\left( {\theta ',\phi '} \right)}\end{array}} \right]} ^{\rm{T}}} \times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}{\exp \left( {j\varPhi _{n,m}^{\theta \theta }} \right)} & {\sqrt {{\kappa ^{ - 1}}} \exp \left( {{\rm{j}}\varPhi _{n,m}^{\theta \phi }} \right)}\\{\sqrt {{\kappa ^{ - 1}}} \exp \left( {j\varPhi _{n,m}^{\phi \theta }} \right)} & {\exp \left( {{\rm{j}}\varPhi _{n,m}^{\phi \phi }} \right)}\end{array}} \right] \times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}{{F_{{\rm{TX}},s,\theta }}\left( {\theta ,\phi } \right)}\\{{F_{{\rm{TX}},s,\phi }}\left( {\theta ,\phi } \right)}\end{array}} \right] \times \exp \left( {{\rm{j}}2{\rm{{\text {π}} }}\lambda _0^{ - 1}\left( {{{{{\Omega}} '}_{n,m}} \cdot {{{d}}_{{\rm{RX}},u}}} \right)} \right) \times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( {{\rm{j2{\text {π}} }}\lambda _0^{ - 1}\left( {{{{\Omega }}_{n,m}} \cdot {{{d}}_{{\rm{TX}},s}}} \right)} \right) \times \exp \left( {{\rm{j2{\text {π}} }}{v_{n,m}}t} \right)\end{array}$

(1)

式中： ${F_{{\rm{RX}},u,\theta '}}$ 、 ${F_{{\rm{RX}},u,\phi '}}$ 分别代表接收天线 $u$ 在方位角和俯仰角方向的场图， ${F_{{\rm{TX}},s,\theta }}$ 、 ${F_{{\rm{TX}},s,\phi }}$ 分别代表发送天线 $s$ 在方位角和俯仰角方向的场图， $\kappa $ 代表天线交叉极化比， ${{{d}}_{{\rm{RX}},u}}$ 是移动用户端天线阵元 $u$ 的位置矢量， ${{{d}}_{{\rm{TX}},s}}$ 是基站端天线阵元 $s$ 的位置矢量， ${\lambda _{\rm{0}}}$ 是载波波长， ${{{\varOmega}} '_{n,m}} = (\sin \theta '\cos \phi ',\sin \theta '\sin \phi ',\cos \theta ')$ 是接收端坐标单位向量， ${P_n}$ 是散射簇 $n$ 对应路径的功率， ${{{\varOmega }}_{n,m}} = $ $ (\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )$ 是发送端的球形坐标单位向量， ${\varPhi ^{AB}}$ 是4种不同极化组合 $AB = \left\{ {\theta \theta ,\theta \phi ,\phi \theta ,\phi \phi } \right\}$ 的随机初始相位，设 ${v_{n,m}}$ 为散射路径分量的多普勒频率。

在包含 $N$ 条路径的信道中，基站的第 $s$ 根天线与用户的第 $u$ 根天线的信道系数时域表达式为所有路径的信道系数和：

${h_{u,s}}(t){\rm{ = }}\sum\limits_{n = 1}^N {{h_{u,s,n}}(t)} $

(2)

1.2 3D MIMO Kronecker模型分析

Kronecker模型假设发送端相关矩阵和接收端相关矩阵是可分离的，最终通过获得的信道相关矩阵来计算信道系数矩阵。下面以式(2)为基础给出3D MIMO Kronecker信道模型。一个MIMO系统由 $S$ 根发射天线和 $U$ 根接收天线组成，信道矩阵H为

${{H}}{\rm{ = }}{\left[ {{h_{u,s}}} \right]_{U \times S}}$

式中： $u = 1,2, \cdots ,U$ ， $s = 1,2, \cdots ,S$ 。

3D MIMO Kronecker信道模型中，信道相关矩阵 ${{{R}}_H}$ 表示为发送端相关矩阵 ${{{R}}_{{\rm{TX}}}}$ 和接收端相关矩阵 ${{{R}}_{{\rm{RX}}}}$ 的Kronecker积，即

${{{R}}_H} = {{{R}}_{{\rm{TX}}}} \otimes {{{R}}_{{\rm{RX}}}}$

式中 ${{{R}}_{{\rm{TX}}}} = {\rm{E}}\left\{ {{{{H}}^{\rm{H}}}{{H}}} \right\}$ 和 ${{{R}}_{{\rm{RX}}}} = {\rm{E}}\left\{ {{{H}}{{{H}}^{\rm{H}}}} \right\}$ 。则 ${{{R}}_{{\rm{TX}}}}$ 计算如下：

${{{R}}_{{\rm{TX}}}} = {\rm{E}}\left\{ {\left[ {\begin{array}{*{20}{c}} {\sum\limits_{u = 1}^U {h_{{u_1}}^ * {h_{{u_1}}}} }&{...}&{\sum\limits_{u = 1}^U {h_{{u_1}}^ * {h_{{u_s}}}} } \\ \vdots &{...}& \vdots \\ {\sum\limits_{u = 1}^U {h_{{u_s}}^ * {h_{{u_1}}}} }&{...}&{\sum\limits_{u = 1}^U {h_{{u_s}}^ * {h_{{u_s}}}} } \end{array}} \right]} \right\}$

取 ${{ R}_{{\rm{TX}}}}$ 矩阵中任意一个元素 ${R_{{\rm{TX}}}}\left( {k,l} \right)$ ，其中 $k,l \leqslant U$ ，可得：

${R_{{\rm{TX}}}}(k,l) = {\rm{E}}\left\{ {\sum\limits_{u = 1}^U {h_{{u_k}}^ * {h_{{u_l}}}} } \right\}$

(3)

结合式(1)可以求得 ${{{R}}_{{\rm{TX}}}}$ 中所有元素。这里对 ${{{R}}_{{\rm{RX}}}}$ 求解过程与上面类似，其矩阵元素 ${R_{{\rm{RX}}}}(k,l)$ 中k、 $l \leqslant S$ ，可得

${R_{{\rm{RX}}}}(k,l) = {\rm{E}}\left\{ {\sum\limits_{s = 1}^S {h_{{k_s}}^ * {h_{{l_s}}}} } \right\}$

则3D MIMO Kronecker模型的信道矩阵表达式为

${{H}}{\rm{ = }}{{R}}_{{\rm{RX}}}^{1/2}{{GR}}_{{\rm{TX}}}^{1/2}$

(4)

式中 ${{G}}$ 是均值为0、方差为1的高斯随机变量组成的复高斯矩阵。

2 3D Massive MIMO信道建模

3D MIMO Kronecker模型虽然可以很好地描述传统MIMO信道的三维传播场景，但缺少对Massive MIMO信道非平稳特性的描述，本文提出的3D Massive MIMO Kronecker模型中采用散射簇在阵列轴上生灭过程演变来建模Massive MIMO信道的非平稳特性。

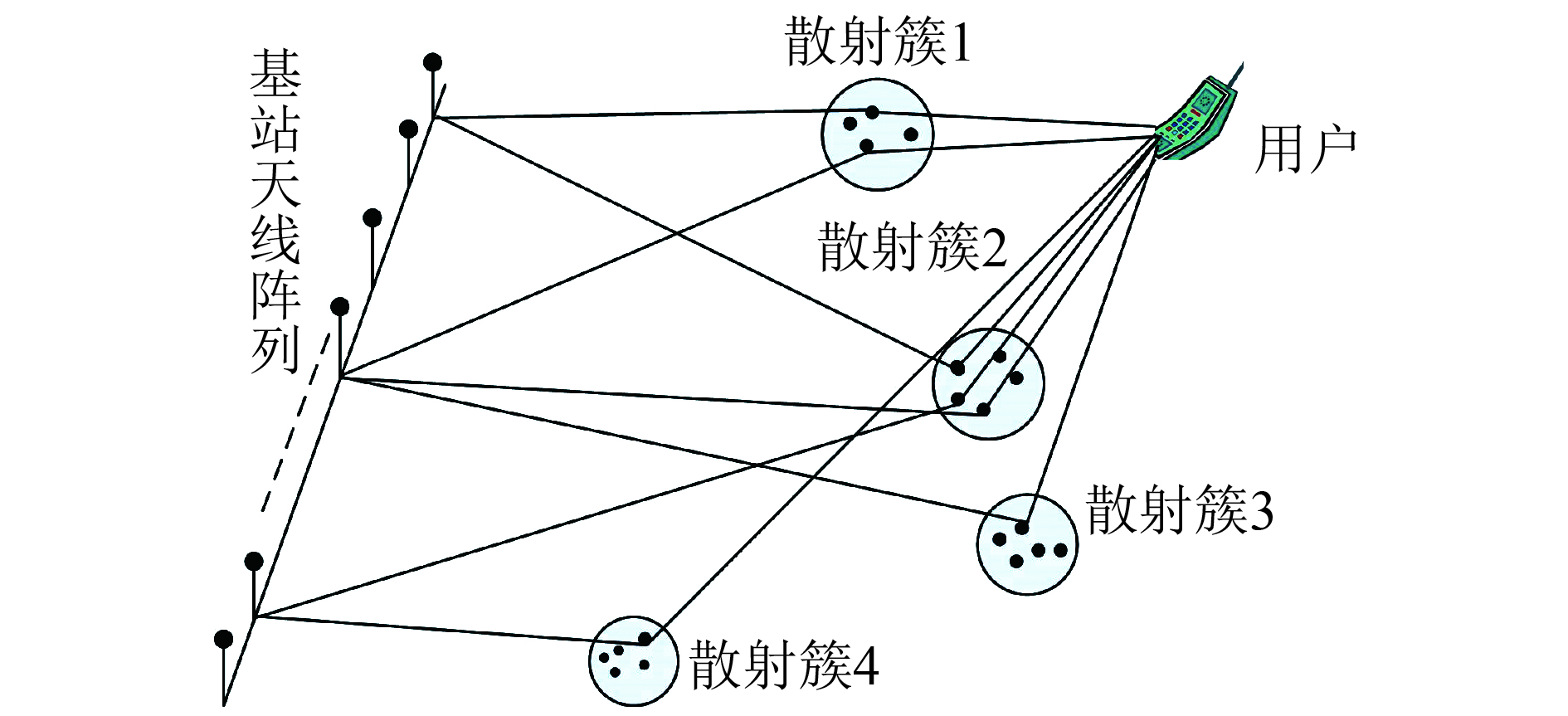
2.1 信道的非平稳特性

通过信道测量发现^[11]，在Massive MIMO系统中任意一个散射簇都不能影响到天线阵列中的所有阵元，散射簇沿着天线阵列轴方向呈现出现或消失现象。由于Massive MIMO系统中不同天线阵元拥有不同的、能够影响其信号传播的散射簇集，因此MIMO信道沿阵列轴展现非平稳特性。图2中以4个散射簇为例描述了散射簇沿阵列轴的变化。这意味着传统MIMO中所有天线阵元拥有同一组散射簇的假设不再适用于Massive MIMO信道。

2.2 生灭过程

生灭过程是文献[12]中提出的一种用以建模信道关于时间轴的非平稳演变的方法。对于Massive MIMO系统，可以利用生灭过程来建模散射簇在阵列轴的非平稳演变。散射簇沿阵列轴的生灭过程包括两部分：首先是散射簇在阵列轴演变过程中的幸存；其次是散射簇演变过程中新散射簇的产生。

散射簇从大规模阵列轴上第 $k$ 条天线到第 $k + 1$ 条天线演变过程中幸存的概率 ${P_{{\rm{TX}}}}$ 可以建模为天线间隔 ${d_T}$ 的指数函数^[13]：

${P_{{\rm{TX}}}} = {{\rm{e}}^{ - \beta {d_T}}}$

式中 $\, \beta \geqslant 0$ ，是描述一个散射簇在阵列轴消失快慢的参数。 ${P_{{\rm{TX}}}}$ 的值随着 ${d_T}$ 增加而减小，这意味着如果2个天线阵元距离越远，共同的散射簇就越少。

此外，阵列轴上散射簇的演变是无记忆的。即从第 $k$ 条天线到第 $l$ 条天线演变过程中散射簇的概率(记为 ${P_{{\rm{TX}}}}(k,l) = {P_{{\rm{TX}}}}\{ k \to l\} $ )等于从第 $k$ 条天线经中间第 $s$ 条天线到第 $l$ 条天线演变过程中散射簇的幸存概率，表示为

$\begin{array}{l}{P_{{\rm{TX}}}}(k,l) = {P_{{\rm{TX}}}}\left\{ {k \to s} \right\}{P_{{\rm{TX}}}}\left\{ {s \to l} \right\} = \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - \beta {d_T}(s{\rm{ - }}k)}}{{\rm{e}}^{ - \beta {d_T}(l - s)}} = {{\rm{e}}^{ - \beta {d_T}\left( {l - k} \right)}}\end{array}$

2.3 3D Massive MIMO Kronecker模型

所提的3D Massive MIMO Kronecker模型和传统3D MIMO Kronecker模型不同点在于，传统模型中所有天线阵元都观察到场景中的所有散射簇，所以传统模型的空间相关函数减小完全由天线之间的空间差异确定。而所提模型空间相关函数的计算不仅与天线间的空间距离相关，而且与天线阵元对应的散射簇集合差异有关。当天线阵列较大时，后者在Massive MIMO信道中更为显著。

散射簇沿阵列轴的演变过程中，从第 $k$ 条天线到第 $l$ 条天线散射簇只有 ${P_{{\rm{TX}}}}(k,l)$ 概率可能幸存并被第 $l$ 条天线观测到。结合天线相关性计算式(3)，所提模型中第 $k$ 条天线和第 $l$ 条天线之间的相关性 ${R'_{{\rm{TX}}}}(k,l)$ 表示为

${R}_{{\rm{TX}}}{^{\rm{'}}}\left( {k,l} \right) = {P_{{\rm{TX}}}}(k,l){R_{{\rm{TX}}}}\left( {k,l} \right)$

也就是说，3D Massive MIMO Kronecker模型中天线相关性等于传统3D MIMO Kronecker模型的天线相关性乘以幸存概率因子。同时，虽然可能有新的散射簇根据生灭过程产生，但这些新产生的散射簇与幸存的散射簇不相关。因此，新生成的散射体对天线相关性没有贡献。

下面考虑散射簇沿天线阵列轴的演变幸存概率。令 ${{{P}}_{{\rm{TX}}}} = {[{P_{{\rm{TX}}}}(k,l)]_{S \times S}},\;\;(k,l = 1,2, \cdots ,S)$ 表示发射端的幸存概率矩阵，由于Massive MIMO系统是在发射端部署大规模天线阵列，而接收端仅有少数天线，因此我们只考虑发射端的散射簇的生灭过程。所提模型中发射端天线相关矩阵 ${R}_{{\rm{TX}}}{^{\rm{'}}}$ 可以表示为

${{ R}}_{{\rm{TX}}}{^{\rm{'}}}{\rm{ = }}{{{R}}_{{\rm{TX}}}} \circ {{{P}}_{{\rm{TX}}}}$

式中“ $ \circ$ ”表示Hadamard积，即两矩阵之间对应位置元素的乘积。

3 仿真分析

首先考察MIMO系统的信道容量，一个MIMO系统由 $S$ 条接收天线和 $U$ 条发送天线组成，则此MIMO系统信道容量可以表示为^[14]

$C = {\log _2}\det [{{{I}}_S} + \frac{\rho }{S}{{H}}{{{H}}^{\rm{H}}}]$

(5)

式中： $\rho $ 是信噪比， ${{{I}}_S}$ 是单位矩阵。将式(4)代入式(5)，则MIMO信道容量为

$C = {\log _2}\det [{{{I}}_S} + \frac{\rho }{S}{{R}}_{{\rm{RX}}}^{1/2}{{G}}{{{R}}_{{\rm{TX}}}}{{{G}}^{\rm{H}}}{{R}}_{{\rm{RX}}}^{{\rm{H}}/2}]$

本文中Massive MIMO系统收发天线阵列设为均匀线性天线阵列结构。下面利用蒙特卡罗实验分析3D Massive MIMO Kronecker模型。我们设置仿真条件如下： $S = 16$ ， $U = 2$ ，发射天线间隔 ${d_T}= $ ${\rm{0.5}}\lambda $ ，接收天线间隔 ${d_R} = 5\lambda $ ，发射功率 $P = 0.01 \;{\rm{W}}$ ，信噪比 ${\rho _0} = 20\; {\rm{dB}}$ ，发射天线位置俯仰角与方位角分别 ${\theta _{{\rm{TX}}}} = 0.25{\rm{{\text {π}} }}$ 和 ${\phi _{{\rm{TX}}}} = 0$ ，接收天线位置俯仰角与方位角分别为 ${\theta _{{\rm{RX}}}} = 0.25{\rm{{\text {π}} }}$ 和 ${\phi _{{\rm{TX}}}} = 0$ ，天线极化角度 $\alpha = 0.25{\text {π}} $ ，交叉极化比 $\kappa $ 的均值和方差分别为7和3。

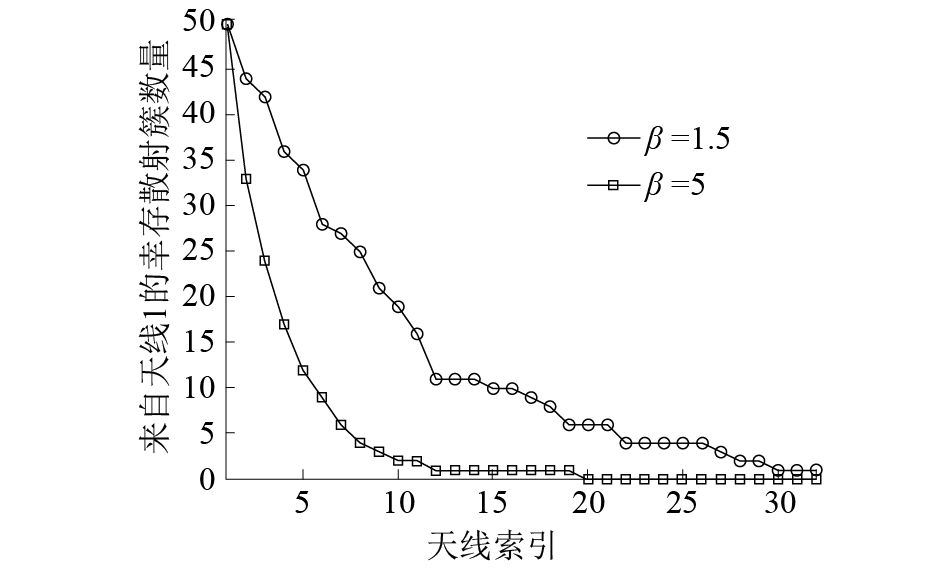
图3展示了散射簇沿着天线阵列轴的演变过程中，参考天线1中的初始散射簇经过生灭过程，幸存的散射簇逐渐减少。从图中可以看出，随着天线索引的增大，共同的散射簇数减少。另外，参数β控制散射簇的幸存概率，β的值可以调整以适应不同的散射环境。

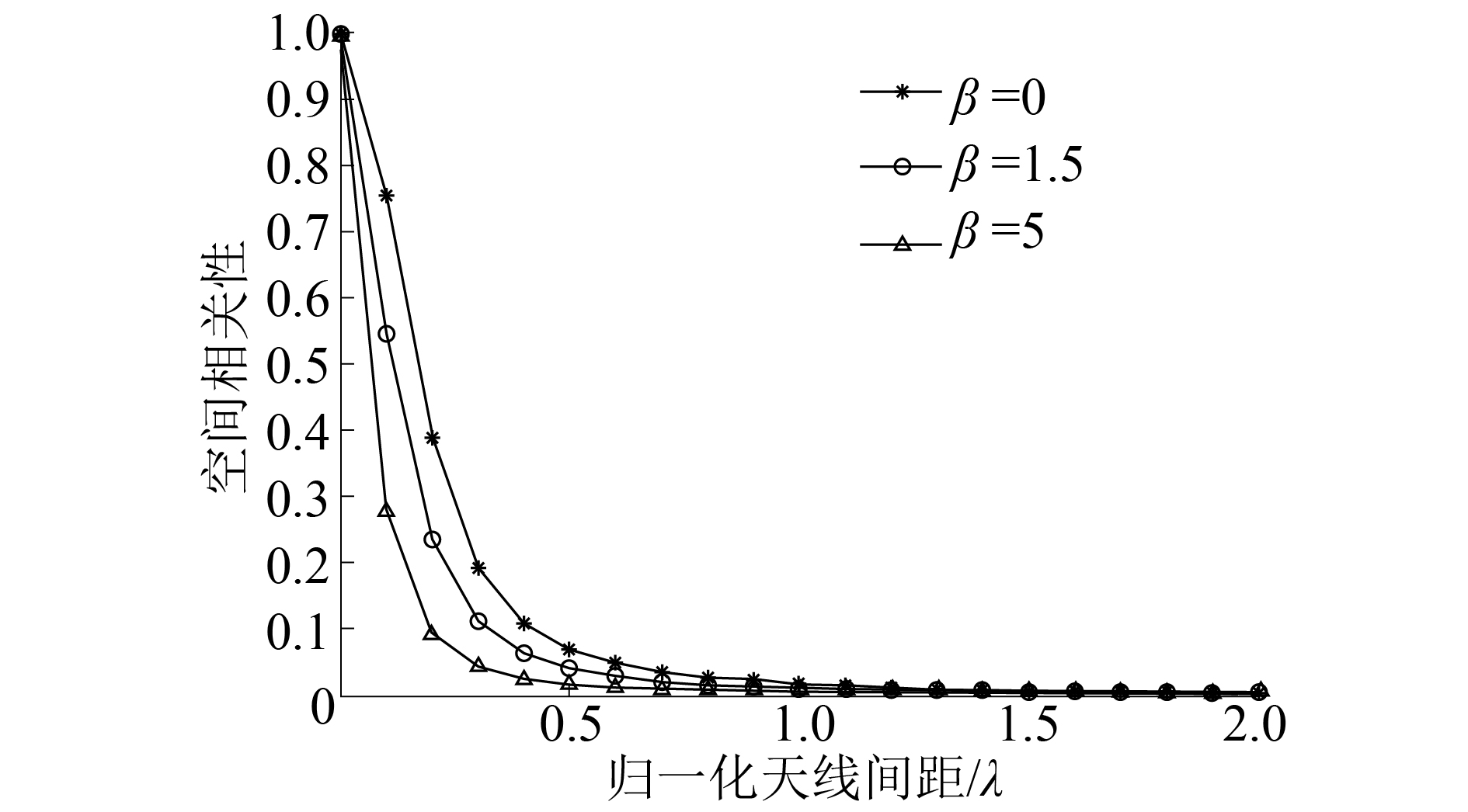
图4展示了3D Massive MIMO Kronecker信道模型不同 $\beta $ 值条件下的天线空间相关性随天线间隔的变化。可以看到，与图中 $\beta {\rm{ = }}0$ 时的传统模型天线空间相关性相比较，所提模型的空间相关性较低。这主要由于Massive MIMO阵列轴上不同天线阵元拥有各自的一组散射簇集，散射簇的非平稳演变降低了MIMO信道的相关性；而所提模型中将阵列轴上散射簇的演变以幸存概率的方式体现，很好地模拟了Massive MIMO信道模型的天线空间相关性。同时参数 $\beta $ 的取值越大将导致天线空间相关性下降更明显，说明不同天线对应的散射簇集差异越大，天线空间相关性越低。

图5给出了不同 $\beta $ 值条件下，3D Massive MIMO Kronecker模型的信道容量随信噪比的变化曲线。可以看出，对应不同的β值有不同的信道容量曲线。当β=0时，3D Massive MIMO Kronecker模型就是传统3D MIMO Kronecker模型，相同信噪比下其信道容量最小；当 $\beta {\rm{ = 50}}$ 时，相同信噪比下其信道容量最大；当 $\beta {\rm{ = 10}}$ 时，模型的信道容量介于以上两者之间。也就是说，随着 $\beta $ 值增加，信道容量得到明显提升，这说明利用散射簇生灭过程建模Massive MIMO信道的非平稳特性后，可以降低MIMO信道模型中的天线相关性并提高信道容量。

4 结论

本文提出一种3D Massive MIMO Kronecker信道模型。该模型以传统3D MIMO Kronecker信道模型的研究为基础，通过生灭过程建模散射簇在阵列轴上的演变，在3D MIMO Kronecker信道模型中对信道相关矩阵的计算考虑散射簇的幸存概率影响，为Massive MIMO系统理论分析和仿真提供了一种更加准确且简单实现的3D分析模型，扩展了Kronecker信道模型的应用。通过仿真实验对比，可以得到以下结论：

1）与传统3D MIMO Kronecker信道模型相比，所提模型更加准确地反映了Massive MIMO的信道特性；

2）所提3D Massive MIMO Kronecker信道模型中对信道相关矩阵的计算考虑了散射簇在阵列轴的演变，总的信道相关矩阵等于天线空间相关矩阵和幸存概率矩阵的Hadamard积；

3）通过计算机仿真实验可以看出，散射簇在天线阵列轴的非平稳演变可以进一步降低Massive MIMO信道的空间相关性。