作为阵列信号处理技术的重要研究方向之一,信号到达角(DOA)估计被广泛应用到雷达、声呐等领域。以MUSIC[1]和ESPRIT[2]为代表的传统空间谱估计算法,实现简单,且空间分辨率高,但要求高信噪比以及多快拍数。随着压缩感知理论的提出与发展,将压缩感知理论应用到阵列信号处理中成为DOA估计算法新的研究方向,学者们提出了大量性能优越的DOA估计算法。其中最为经典的是由D.Malioutov等人提出的
针对此问题,首先假设空间中存在一个均匀线阵用于接收空间窄带目标信号,对空间进行网格划分使得空间信号稀疏化,从而完成信号稀疏表示,并得出可通过求解
假设
| ${{y}}(t) = {{As}}(t) + {{n}}(t)$ |
式中:
空间信号是可稀疏的,通过特定的网格划分可将空间信号稀疏化。将空间均匀划分为
| ${{x}}(t) = {[{x_1}(t),{x_2}(t), \cdots ,{x_N}(t)]^{\rm{T}}}$ |
| ${{\varPhi}} {\rm{ = }}[{{a}}({\theta _1}),{{a}}({\theta _2}), \cdots ,{{a}}({\theta _N})]$ |
则稀疏表示模型下的DOA估计数学模型为
| ${{y}}(t) = {{\varPhi}} {{x}}(t) + {{n}}(t)$ | (1) |
通过求解如下
| $\left\{ {\begin{array}{*{20}{l}}{\hat { x} = \arg \min {{\left\| { x} \right\|}_1}}\\{{\rm s.t.}{{\left\| {{ y} - { {Ax}}} \right\|}_2}\sigma }\end{array}} \right.$ |
式中
稀疏贝叶斯理论适用于对实数数据的处理,而阵列接收数据是复数,为了将该理论应用到DOA估计中,需要将观测数据实数化以构建实数域的优化模型,因此式(1)需改写为
| $\left( {\begin{array}{*{20}{c}} {{\rm Re}({{y}})} \\ {\rm{Im}} ({{y}})\end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\rm Re}({{\varPhi}} )}&{ - \rm{Im} ({{\varPhi}} )} \\ {\rm{Im} ({{\varPhi}} )}&{R({{\varPhi}} )} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\rm Re}({{x}})} \\ {\rm{Im}} ({{x}}) \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\rm Re}({{n}})} \\ {\rm{Im}} ({{n}}) \end{array}} \right)$ |
式中
对于压缩感知下的DOA估计模型:
| ${{y}} = {{\varPhi}} {{x}} + {{n}}$ |
式中:
从而可以得到
| $\begin{gathered} p({{y}}\left| {{x}} \right.,{\sigma ^2}) = \prod\limits_{n = 1}^N {p({{{y}}_n}\left| {{{{\varPhi}} _n}} \right.{{x}},{\sigma ^2})} {\rm{ = }} \hfill \\\quad\quad\quad\quad\quad{\rm{ (2{\text π}}}{\sigma ^2}{{\rm{)}}^{ - \frac{N}{2}}}\exp {( - \frac{1}{{2{\sigma ^2}}}\left\| {{{y}} - {{\varPhi}} {{x}}} \right\|)^2} \hfill \\ \end{gathered} $ |
根据贝叶斯估计理论,需要对参数
| $p({{x}}\left| {{\alpha}} \right.) = \prod\limits_{i = 1}^N {N({x_i}\left| 0 \right.,{\alpha _i}^{ - 1})} $ |
式中
| $p({{\alpha}} ) = \prod\limits_{i = 1}^N {\varGamma ({\alpha _i}\left| a \right.,b)} $ |
| $p({\alpha _0}) = \varGamma ({\alpha _0}\left| c \right.,d)$ |
式中
| $\varGamma (\xi \left| {a,b} \right.) = \frac{{{b^a}}}{{\varGamma (a)}}{\xi ^{a - 1}}\exp ( - b\xi )$ |
根据贝叶斯理论,可以得到待估计参数的最大后验概率分布为
| $p({{x}},{{\alpha}} ,{\alpha _0}|{{y}}) = \frac{{p({{y}}|{{x}},{{\alpha}} ,{\alpha _0})p({{x}},{{\alpha}} ,{\alpha _0})}}{{p({{y}})}}$ |
| $p({{y}}) = \iiint {p({{y}}|{{x}},{{\alpha}} ,{\alpha _0})}p({{x}},{{\alpha}} ,{\alpha _0}){\rm{d}}{{x}}{\rm{d}}{{\alpha}} {\rm{d}}{\alpha _0}$ |
| $p({{x}},{{\alpha}} ,{\alpha _0}|{{y}}) = p({{x}}|{{y}},{{\alpha}} ,{\alpha _0})p({{\alpha}} ,{\alpha _0}|{{y}})$ |
然后再利用积分求解
设由未知待估计参数
| ${{\vartheta}} = \left\{ {{{{\vartheta}} _1},{{{\vartheta}} _2},{\vartheta _3}} \right\} = \left\{ {{{x}},{{\alpha}} ,{\alpha _0}} \right\}$ |
观测量
| $p({{y}}){\rm{ = }}\frac{{p({{y}},{{\vartheta}} )}}{{p({{x}},{{\vartheta}} |{{y}})}}$ | (2) |
依据变分理论,在式(2)中引入一个关于参数集
| $p({{y}}){\rm{ = }}{{\frac{{p({{y}},{{\vartheta}} )}}{{q({{\vartheta}} )}}} / {\frac{{p({{{{\vartheta}}}} |{{y}})}}{{q({{\vartheta}} )}}}}$ | (3) |
对式(3)两边取对数得
| $\ln (p({{y}})) = \ln \frac{{p({{y}},{{\vartheta}} )}}{{q({{\vartheta}} )}} - \ln \frac{{p({{\vartheta}} |{{y}})}}{{q({{\vartheta}} )}}$ | (4) |
设
| $\begin{gathered} \ln (p({{y}})) = \iiint {q({{\vartheta}} )\ln \frac{{p(y,{{\vartheta}} )}}{{q({{\vartheta}} )}}}{\rm{d}}{{{\vartheta}} _1}{\rm{d}}{{{\vartheta}} _2}{\rm{d}}{\vartheta _3} - \hfill \\ \quad\quad\quad\quad{\rm{ }}\iiint {q({{\vartheta}} )\ln \frac{{p({{\vartheta}} |{{y}})}}{{q({{\vartheta}} )}}}{\rm{d}}{{{\vartheta}} _1}{\rm{d}}{{{\vartheta}} _2}{\rm{d}}{\vartheta _3} \hfill \\ \end{gathered} $ | (5) |
式(5)简记为
| $\ln (p({{y}})){\rm{ = }}L(q({{\vartheta}} )) + {\rm{KL}}(q({{\vartheta}} )||p({{\vartheta}} |{{y}}))$ |
| $L(q({{\vartheta}} )){\rm{ = }}\iiint {q({{\vartheta}} )\ln \frac{{p({{y}},{{\vartheta}} )}}{{q({{\vartheta}} )}}}{\rm d}{{{\vartheta}} _1}{\rm d}{{{\vartheta}} _2}{\rm d}{\vartheta _3}$ |
| ${\rm{KL}}(q({{\vartheta}} )||p({{\vartheta}} |{{y}})){\rm{ = }} - \iiint {q({{\vartheta}} )\ln \frac{{p({{\vartheta}} |{{y}})}}{{q({{\vartheta}} )}}}{\rm{d}}{{{\vartheta}} _1}{\rm{d}}{{{\vartheta}} _2}{\rm{d}}{\vartheta _3}$ |
式中
根据均值域理论,关于
| $q({{\vartheta}} ) = q({{x}},{{\alpha}} ,{\alpha _0}){\rm{ = }}q({{x}})q({{\alpha}} )q({\alpha _0})$ |
各参数服从以下分布:
| $q({{x}}){\rm{ = }}N({{x}}|\overline {{u}} ,\overline {{\varSigma}} )$ |
| $q({{\alpha}} ){\rm{ = }}\sum\limits_{m = 1}^N {\varGamma ({\alpha _m}|{{\overline a }_m},{{\overline b }_m})} $ |
| $q({\alpha _0}){\rm{ = }}\varGamma ({\alpha _0}|\overline c ,\overline d )$ |
式中:
| $\overline {{u}} = {\alpha _0}\overline {{\varSigma}} {{{\varPhi}} ^{\rm{T}}}{{y}}$ | (6) |
| $\overline {{\varSigma}} {\rm{ = (diag}}({\alpha _m}) + {\alpha _0}{{{\varPhi}} ^{\rm{T}}}{{\varPhi}} {)^{ - 1}}$ | (7) |
| ${\overline a_m} = a + 1/2$ | (8) |
| ${\overline b_m} = b + \frac{{|\overline {{u}} {|^2} + {{\bar {{\varSigma}} }_{mm}}}}{2}$ | (9) |
| $\overline c = c + (N + 1)/2$ | (10) |
| $\overline d = d + \frac{{||{{y}} - {{\varPhi}} \overline {{\mu}} |{|^2} + {\rm{tr}}(\overline {{\varSigma}} {{{\varPhi}} ^{\rm{T}}}{{\varPhi}} )}}{2}$ | (11) |
| ${\alpha _m} = {\overline a_m}/{\overline b_m}$ |
| ${\alpha _0} = \overline c/\overline d$ |
式中:
对于变分贝叶斯学习方法,是通过监控下界[13]
| $\begin{gathered} L(q({{x}},{{\alpha}} ,{\alpha _0})) = \left\langle {\ln p({{y}}|{{x}},{\alpha _0})} \right\rangle + \left\langle {\ln p({{x}}|{{\alpha}} )} \right\rangle + \hfill \\ \quad\quad\quad\quad\quad\quad\;\,\left\langle {\ln p({{\alpha}} )} \right\rangle + \left\langle {\ln p({\alpha _0})} \right\rangle - \left\langle {\ln q({{x}})} \right\rangle - \hfill \\ \quad\quad\quad\quad\quad\quad\;\,\left\langle {\ln q({{\alpha}} )} \right\rangle - \left\langle {\ln q({\alpha _0})} \right\rangle \hfill \\ \end{gathered} $ |
在计算
| $\begin{gathered} L(q({{x}},{{\alpha}} ,{\alpha _0})){\rm{ = }}\frac{1}{2}\ln |\overline {{\varSigma}} | - {\overline a _m}\sum\limits_{m = 1}^M {\ln {{\overline b }_m}} + \hfill \\ \quad\quad\quad\quad\quad\;\;\;\;{\rm{ }}\frac{1}{2}\sum\limits_{m = 0}^{N - 1} {\ln {{\overline {{\varSigma}} }_{mm}}} - \overline c \ln \overline d + {L_{{\rm{const}}}} \hfill \\ \end{gathered} $ | (12) |
| $\begin{gathered} {L_{{\rm{const}}}} = - \frac{N}{2}\ln 2{\rm{{\text π}}} + \frac{{M + N}}{2} - \hfill \\ \quad\quad\;\;\;{\rm{ }}(M + N + 1)\ln \varGamma (a) + (M + N + 1)a\ln b + \hfill \\ \quad\quad\;\;\;{\rm{ }}(M + N)\ln \varGamma ({{\overline a}_m}) + \ln \varGamma (\overline c) \hfill \\ \end{gathered} $ |
式中
基于变分稀疏贝叶斯的DOA估计算法流程如下:
输入:观测向量
输出:重构信号
1)初始化
2)利用式(6)和(7)更新
3)利用式(8)~(11)更新
4)利用式(12)更新
5)如果:
为评估基于稀疏变分贝叶斯学习的DOA估计算法的性能,本文通过MATLAB仿真比较在单快拍条件下基于VSBL的DOA估计算法和基于SBL的DOA估计算法分别在不同信噪比、不同阵元数下的DOA估计误差及其成功率以及算法运行时间。
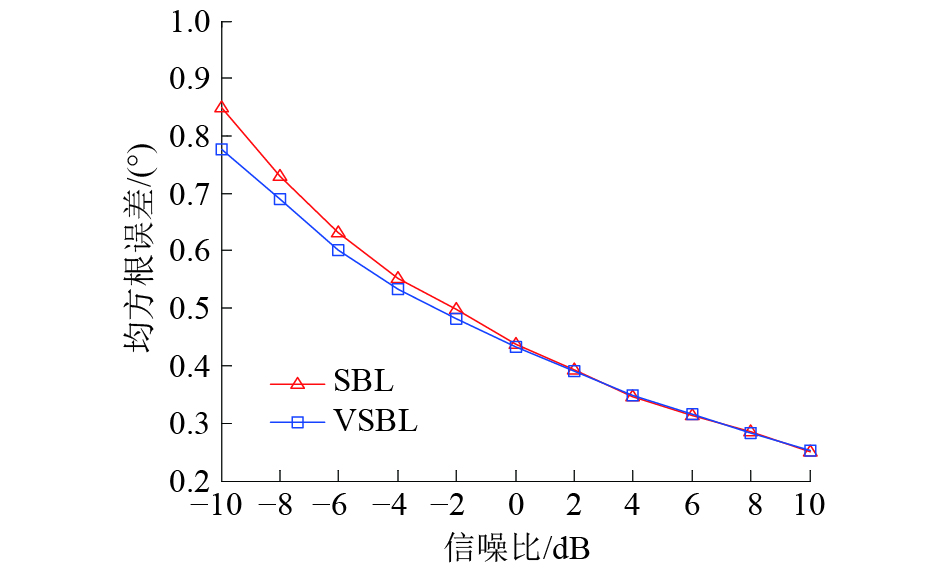
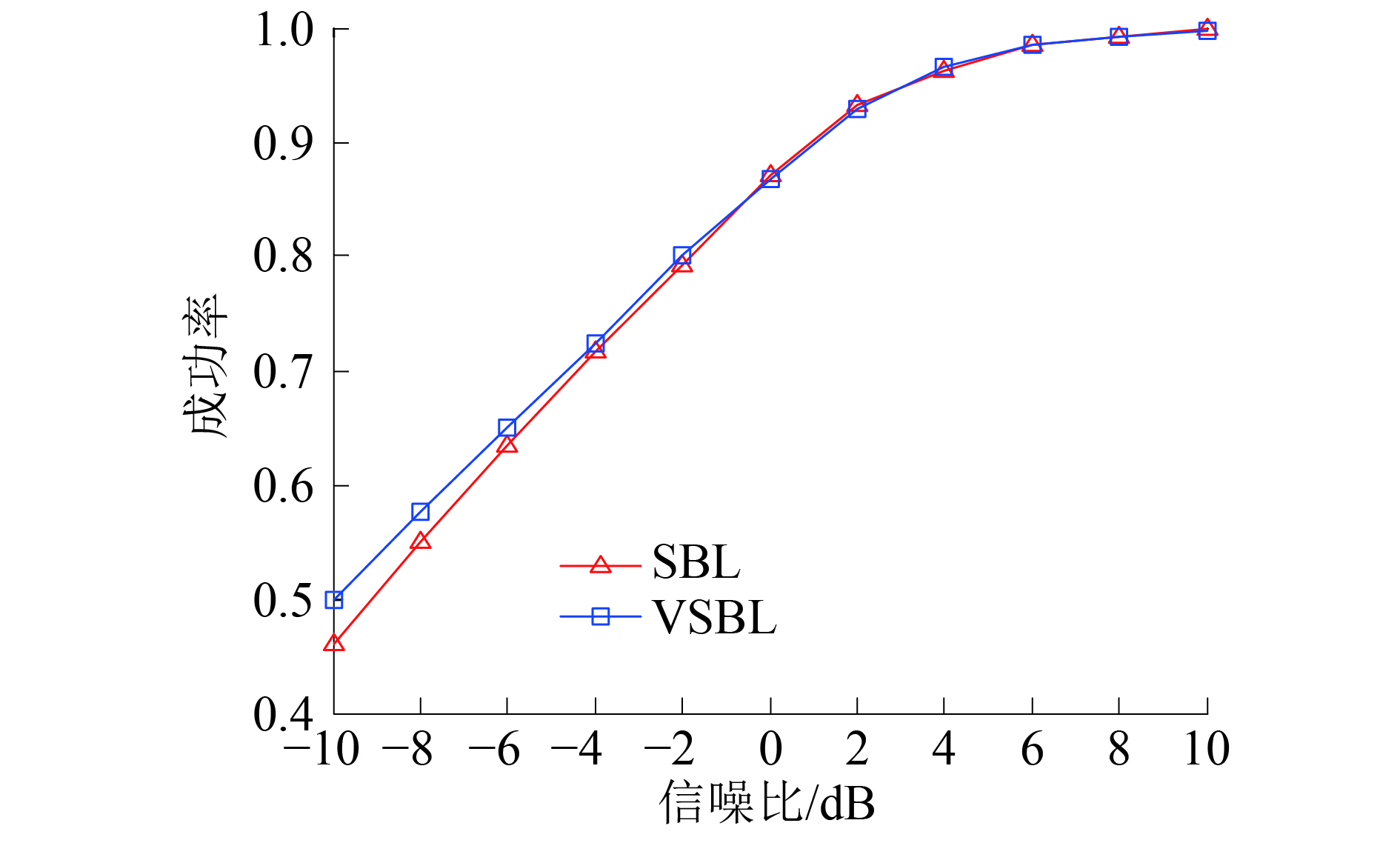
3.1 不同信噪比下的DOA估计结果比较假设空间中存在由20个阵元组成的均匀线阵,同时有2个信号分别以入射角10°和20°入射到该阵列中,信号的信噪比以2 dB为步进,从−10 dB到10 dB变化。用2种算法比较不同信噪比下的DOA估计结果,如果所估计出角度在误差允许范围内,则认为本次实验是成功的,每个条件下的实验进行500次,并统计各条件下的DOA估计误差及其成功率,如图1、2所示。由图1、2可以得出,随着信噪比的增加,基于VSBL的DOA估计算法和基于SBL的DOA估计算法的DOA估计精度和成功率会一直提高,而且在高信噪比下,2个算法的DOA估计精度以及成功率相差不大,但是在低信噪比下,基于VSBL的DOA估计算法的DOA估计精度以及成功率要高于基于SBL的DOA算法。
|
Download:
|
| 图 1 不同信噪比下的DOA估计误差 | |
|
Download:
|
| 图 2 不同信噪比下的DOA估计成功率 | |
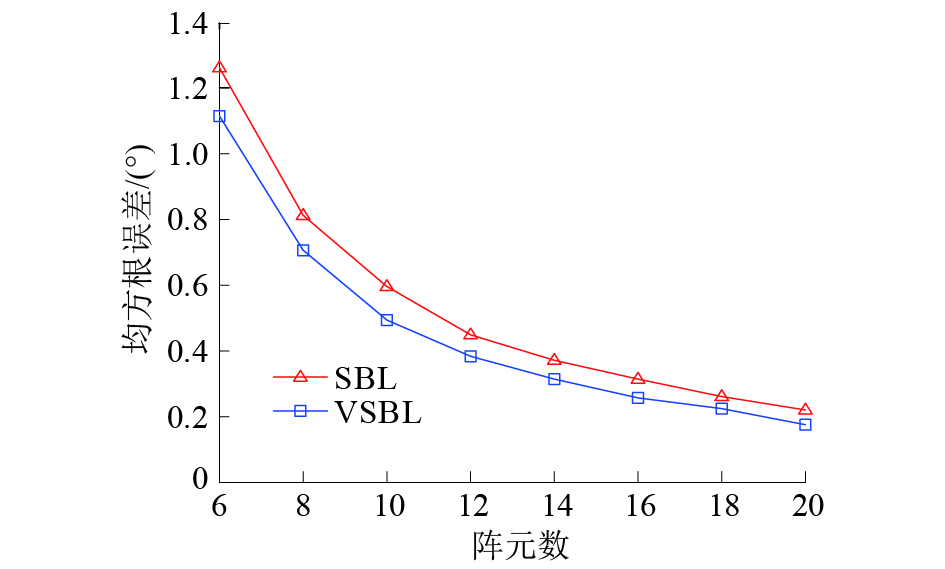
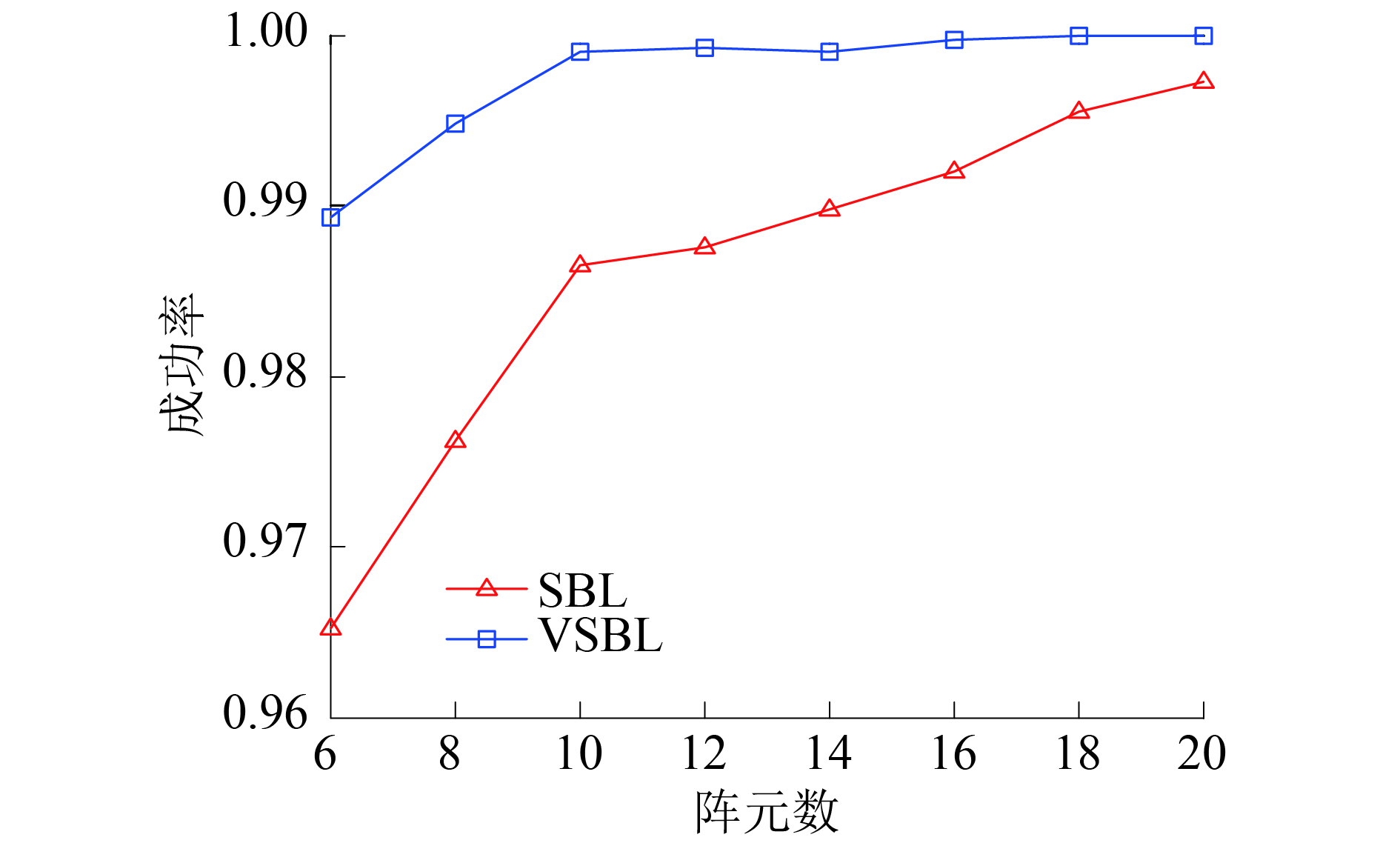
假设空间中存在一个均匀线阵,且同时有2个信号分别以入射角10°和20°入射到该阵列中,阵元数以2为步进从6阵元到20阵元变化,信噪比为15 dB,用2种算法比较不同阵元数下的DOA估计结果。如果所估计出角度在误差允许范围内,则认为本次实验是成功的,每个条件下的实验进行500次,并统计各条件下的DOA估计误差及其成功率,如图3、4所示。由图3、4可以得出,在不同的阵元数下,基于VSBL的DOA估计算法的DOA估计精度要明显高于基于SBL的DOA估计算法。而且基于VSBL的DOA估计算法在阵元数为10时就能以接近100%的重构概率估计出信号的DOA,而基于SBL的DOA估计算法在阵元数为20时才能以接近100%的重构概率估计出信号的DOA。
|
Download:
|
| 图 3 不同阵元数下的DOA估计误差 | |
|
Download:
|
| 图 4 不同阵元数下的DOA估计成功率 | |
仿真条件:阵元数为20,信噪比比为15 dB,蒙特卡罗仿真次数为500次。仿真所用CPU为:Intel(R) Core(TM) i5-4570,运行内存为4 GB,MATLAB版本为R2014。
基于BCS的DOA估计算法运行时间为212 s。而基于VBCS的DOA估计算法的运行时间为92 s。
由算法运行时间结果可知,基于VBCS的DOA估计算法的运行时间要小于基于BCS的DOA估计算法的运行时间。因此基于VBCS的DOA估计算法的收敛速度要快于基于BCS的DOA估计算法收敛速度。
4 结论本文提出了一种基于VSBL的DOA估计算法。首先建立了基于稀疏表示的DOA估计模型,并在此基础上建立了稀疏贝叶斯模型。然后通过变分贝叶斯学习算法的引入,简化了稀疏贝叶斯模型中最大后验概率的求解,并总结出该DOA估计算法的求解步骤。最后通过仿真比较了基于VSBL的DOA估计算法和基于SBL的DOA估计算法的性能,并得出以下结论:
1)本文算法在低信噪比下具有更高的DOA估计精度以及成功率,更有利于在复杂电磁环境下DOA估计的应用;
2)本文算法可通过更少的振元数高精度、高成功率估计出信号到达角,从而减轻硬件对大量数据存储、传输和处理的压力;
3)本文算法具有更低的算法复杂度,大幅度减少了算法的运行时间,更有利于DOA估计实时性要求的实现;
4)本文算法只适用于单快拍下的DOA估计问题,将该思想引用到多快拍下的DOA估计问题是下一步的研究方向。
| [1] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE transactions on antennas and propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 ( 0) 0)
|
| [2] |
ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE transactions on acoustics, speech, and signal processing, 2002, 37(7): 984-995. ( 0) 0)
|
| [3] |
李鹏飞, 张旻, 钟子发. 基于稀疏表示的宽带DOA估计[J]. 电子测量与仪器学报, 2011, 25(8): 716-721. ( 0) 0)
|
| [4] |
赵永红, 张林让, 刘楠, 等. 一种新的基于稀疏表示的宽带信号DOA估计方法[J]. 电子与信息学报, 2015, 37(12): 2935-2940. ( 0) 0)
|
| [5] |
燕学智, 温艳鑫, 刘国红, 等. 基于稀疏表示和近似范数约束的宽带信号DOA估计[J]. 航空学报, 2017, 38(6): 320705. ( 0) 0)
|
| [6] |
李鹏飞, 张旻, 钟子发. 基于空间角稀疏表示的二维DOA估计[J]. 电子与信息学报, 2011, 33(10): 2402-2406. ( 0) 0)
|
| [7] |
刘永花, 周围. 基于协方差矩阵稀疏表示的相干源DOA估计算法[J]. 电子世界, 2017(6): 118-120. DOI:10.3969/j.issn.1003-0522.2017.06.087 ( 0) 0)
|
| [8] |
庞慧, 陈俊丽. 基于稀疏贝叶斯的二维DOA估计算法研究[J]. 工业控制计算机, 2017, 30(10): 90-91, 94. DOI:10.3969/j.issn.1001-182X.2017.10.039 ( 0) 0)
|
| [9] |
YANG Jie, LIAO Guisheng, LI Jun. An efficient off-grid DOA estimation approach for nested array signal processing by using sparse Bayesian learning strategies[J]. Signal processing, 2016, 128: 110-122. DOI:10.1016/j.sigpro.2016.03.024 ( 0) 0)
|
| [10] |
SI Weijian, QU Xinggen, QU Zhiyu, et al. Off-grid DOA estimation via real-valued sparse bayesian method in compressed sensing[J]. Circuits, systems, and signal processing, 2016, 35(10): 3793-3809. DOI:10.1007/s00034-015-0221-3 ( 0) 0)
|
| [11] |
高阳, 陈俊丽, 杨广立. 基于酉变换和稀疏贝叶斯学习的离格DOA估计[J]. 通信学报, 2017, 38(6): 177-182. ( 0) 0)
|
| [12] |
孙磊, 王华力, 许广杰, 等. 基于稀疏贝叶斯学习的高效DOA估计方法[J]. 电子与信息学报, 2013, 35(5): 1196-1201. ( 0) 0)
|
| [13] |
BISHOP C M, TIPPING M. Variational relevance vector machines[C]//Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence. San Francisco, USA, 2000: 46−53.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


