多分类系统（multiple classifier system，MSC）通过对基分类器的选择与组合，能够获得比任何一个单一分类器更好的分类性能^[1]，近年来在高光谱图像中得到较为广泛的应用^[2]。构建多分类系统主要有3种结构：并行结构、串行结构和混合结构。目前高光谱图像分类中主要应用并行结构为主，即使用多个分类器进行并行训练，然后结合某种选择和权值策略进行结果的组合。组合策略主要有投票法^[3]、贝叶斯平均法^[4]、统计意见一致法^[5]、证据理论^[4]和模糊积分法^[6]。Du等^[7]对这些组合策略进行了全面的比较，发现其精度相当，但是投票的方式操作简单，而且不需要先验知识，因此得到广泛的应用。但是基于投票的分类器同样存在限制，即要求差异化的分类器和相似的分类性能作为前提保障，因此在实际的分类过程中，需要一定的经验进行分类器的挑选和参数训练。Wolpert^[8]提出的Stacking Learning是一种类串连形式多层集成系统，它使用交叉验证和K-Fold的方式进行后验概率特征重组，形成Meta数据进行二级训练，目前被应用于多个领域。Escalera等^[9]使用Stacked Sequential Learning结合音频和视屏中人物的面对面谈话，将对话中的笑声进行识别检测，实验结果表明该方法的表现要好于AdaBoost。Razmara和Sarkar^[10]将Stacking Learning的衍生算法应用到机器翻译系统中，在2个语种的翻译评估中表现要好于贝叶斯平均法构成的组合分类器。Stacking learning还在神经医学、药物学等领域起到重要作用，它帮助医生进行多医疗器械诊断结果的结合，如区分阿尔茨海默病和良性的认知障碍、简易精神状态检测等^[11]，实验显示，使用Stacking Learning的方式比传统k-NN方法提高了7%。但Stacking Learning鲜有在图像领域尝试，本文将Stacking Learning引入到高光谱图像的分类中，采用目前较为流行和新型的3种有监督算法支持向量机（support vector machine，SVM），旋转森林（RotationForest）^[12]和Extreme Gradient Boosting（XGBoost）^[13]当做基分类器构建Stacking过程，与传统并行集成学习进行比较，获得了更好的分类效果。

1 相关工作 1.1 旋转森林

旋转森林最早是由Rodriguez^[14]提出的，是一种基于随机森林（RandomForest, RF）的方法。它先将原始数据变换投影到新的特征空间，然后用来训练每个基础分类器（决策树），目的是为了每个基础分类器获得较高的准确率和多样性。其中特征变换方法包括主成分分析、最大噪声比变换、独立成分分析和局部Fisher判别分析等。

RotationForest过程描述如下：训练样本集 ${{X}} = {\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right]^{\rm{T}}}$ 包含了n个特征，用X代表 $N \times n$ 大小的训练集矩阵。使用 ${{Y}} = {\left[ {{y_1},{y_2}, \cdots ,{y_n}} \right]^{\rm{T}}}$ 代表数据的类别标签，其中类别包含 $\left\{ {1,2, \cdots ,c} \right\}$ ，c是类别总数。定义 ${\varGamma _1},{\varGamma _2}, \cdots ,{\varGamma _L}$ 为用于集成的分类器，F为特征集，训练基础分类器 ${\varGamma _i},i=1,2,\cdots,L$ 。其步骤如下。

1）将F分割成K个特征子集，每个特征子集包含了M=n/K个特征。

2） ${F_{i,j}}$ 表示第j个特征子集，其中 $ j=1,2, \cdots,K$ 。根据 ${F_{i,j}}$ 从X中找到对应的训练集 ${X_{i,j}}$ ，对每组 ${X_{i,j}}$ 按75%进行Bootstrap采样，将新的采样样本定义为 $X_{i,j}{^{'}}$ 。然后使用特征变换的方法将其转化为对应系数 ${{a}}_{_{i,j}}^{(1)}\;{{a}}_{_{i,j}}^{(2)},\cdots, {{a}}_{_{i,j}}^{({M_j})},{{{a}}'_{i,j}}$ 是一个 $M \times 1$ 的矩阵。

3）稀疏旋转矩阵 ${{{R}}_i}$ 由上述系数构成，表现形式如下：

${{{R}}_i} = \left[ {\begin{array}{*{20}{c}} {a_{i,1}^{(1)},{a^{(2)}_{i,1}},\cdots,a_{i,1}^{({M_1})}}&0& \cdots &0 \\ 0&{a_{i,2}^{(1)},{a^{(2)}_{i,2}},\cdots,a_{i,2}^{({M_2})}}& \cdots &0 \\ \vdots & \cdots & \cdots & \vdots \\ 0&0& \cdots &{a_{i,K}^{(1)},{a_{i}^{(2)}{,k}},\cdots,a_{i,K}^{({M_K})}} \end{array}} \right]$

矩阵 ${{{R}}_i}$ 的各列数据都是原始特征经过变换后的数据 ${{R}}_i^a$ ，然后训练集就会变成X ${ R}_i^a$ 的形式，之后再由基础分类器进行并行训练。

当给定一个测试样本 $\chi $ ，使用式（1）能够计算出每一类的置信度。

${\mu _k}(\chi ) = \frac{1}{L}\sum\limits_{i = 1}^L {{\gamma _{i,k}}(\chi { R}_i^a)} ,k = 1,2,\cdots,c$

(1)

式中： ${\gamma _{i,k}}(\chi { R}_i^a)$ 表示分类器 ${\varGamma _i}$ 给出的样本， $\chi $ 属于类别k的后验概率。最后一步， $\chi $ 会将后验概率最大的类当做判断的类别，旋转森林过程结束。

Xia等^[15]在高光谱图像的实验中表明，Rotation-Forest方法要优于传统的随机森林、AdaBoost、SVM等分类器，故在本次实验中作为基础分类器使用。

1.2 XGBoost方法

XGBoost和迭代决策树（gradient boosting decision tree，GBDT）同为Boosting方法，但XGBoost在大规模机器学习上有着无与伦比的优势。因此XGBoost在世界范围内的数据挖掘及机器学习竞赛中炙手可热。限于篇幅原因，XGBoost原理推导不再赘述，可参考文献[13]。这里给出相较于其他传统的提升决策树，XGBoost所具有的优势。

1）XGBoost在代价函数时进行二阶泰勒展开，同时用到了一阶和二阶导数，在损失函数的定义上更加精确。而GBDT则只使用了一阶导。

2）XGBoost在代价函数中加入了正则项，能够很好地控制模型的训练过程，防止训练出来的模型存在过拟合现象。其正则项中包含了树的叶子节点个数等。

3）XGBoost使用类似随机森林的方式采用列抽样，使之减少计算量的同时还能防止过拟合。

4）XGBoost是Boosting的方法，本身并不支持并行计算，但是它会对特征进行分块处理，形成多块Block并排序，能够在迭代过程中不断使用这个中间件寻找最佳的分裂点，极大地减少了计算时间。简单说就是在特征的粒度上进行了并行化处理而非算法本身。

总体来说，XGBoost是一种高度可扩展的树结构增强模型，能够很好地处理稀疏数据，在超大规模的数据训练中能够极大提升算法速度及压缩计算内存。由于XGBoost应用于图像的研究较少，本文在此对其实验算法进行研究。

2 Stacking Learning

Stacking是Stacked Generalization的简称^[8]，最先由Wolpert提出，实质上是一种串行结构的多层学习系统，Stacking Learning前期使用交叉验证的形式进行原始特征向二级特征进行转化，之后对转化后的二级新特征进行常规训练和分类过程。与其他传统的集成学习如Bagging、Boosting不一样，Stacking Learning使用不同的基分类器进行组合。由于不同分类器对数据的训练存在差异，因此将从不同的角度探索假设空间，从而产生一个不同的分类器池，当他们的预测结合在一起时，预期的结果模型比每个基分类器更加准确。为了更好地描述Stacking的多级处理过程，Stacking Learning引入了基分类器（Base-Classifier）和元分类器（Meta-Classifier）概念，其中基分类器使用原始特征进行训练，其输出结果作为二级新的特征；而元分类器将重新训练二级特征并形成最终的判决分类器。Stacking Learning结构框架主要分为Level-0和Level-1这2层，如图1所示。

在Level-0层首先对训练集 $S$ 使用类似J-Fold的方式将数据分成J个部分 ${S_1},S_2,\cdots,{S_j}$ 。对于第j次训练，先将 ${S_j}$ 这一部分数据保留出来，然后将 ${S^{( - j)}} = S - {S_j}$ 用来训练每一个基础分类器K_j，训练完成后，使用每个基础分类器对数据 ${S_j}$ 进行预测分类，产生该数据的所属各类别的后验概率。若训练数据存在N个类别，那么每个基础分类器将会产生N个由后验概率组成的新的特征维度p_kj，K个分类器将组成K×N个新维度，这些新增的特征维度将作为Level-1中的训练数据，称之为Meta-data。根据J-Fold的原理，算法结束时将会计算J次，直至训练集中的所有数据都被转换成由后验概率构成的新数据，Level-0阶段结束。由于使用到了交叉验证技术，故训练集并不会存在数据泄露问题。值得注意的是，在Level-0阶段，Meta data是由基分类器对原始训练集的预测判断，相较于原始的特征集，属于强特征，同时也达到了降维的作用。在Level-1阶段，可以使用任何分类器进行训练，最后获得一个Meta Classifier模型，基本的Stacking Learning过程结束。

当需要验证模型效果时，首先需要对验证集的数据进行同样的特征变换。原因在于Meta Classifier学习到的特征是由Base Classifier对原始训练集交叉验证的结果，Meta data数据特征空间已经发生变化，故测试集也要先经过K个分类器重新生成新的特征，然后再使用Meta Classifier进行预测。

3 实验与分析 3.1 实验数据及设置 3.1.1 实验数据

AVIRIS印第安纳数据集是Indian Pine实验区的高光谱图像数据。它是通过机载可见光/红外成像光谱仪器得到的。波段数目是224，空间分辨率是20 m，图像尺寸是 $145\;{\text{像素}} \times 145\;$ 像素，波长为0.4~2.5 μm。去除24个噪声波段和水汽吸收波段后，图像剩余波段数目为200个，共包含16种地物，共10 249个样本。

3.1.2 实验设置

实验数据使用Indian Pines的16类全地物进行实验，评价指标采用总体分类精度（overall accuracy，OA）、平均分类精度（average accuracy，AA）和Kappa系数。

对比算法包括SVM、XGBoost、RotationForest、RF、GBDT。根据文献[7]的研究表明不同组合策略构成的并行集成算法精度相当，故使用基于投票的并行集成算法进行比较实验。

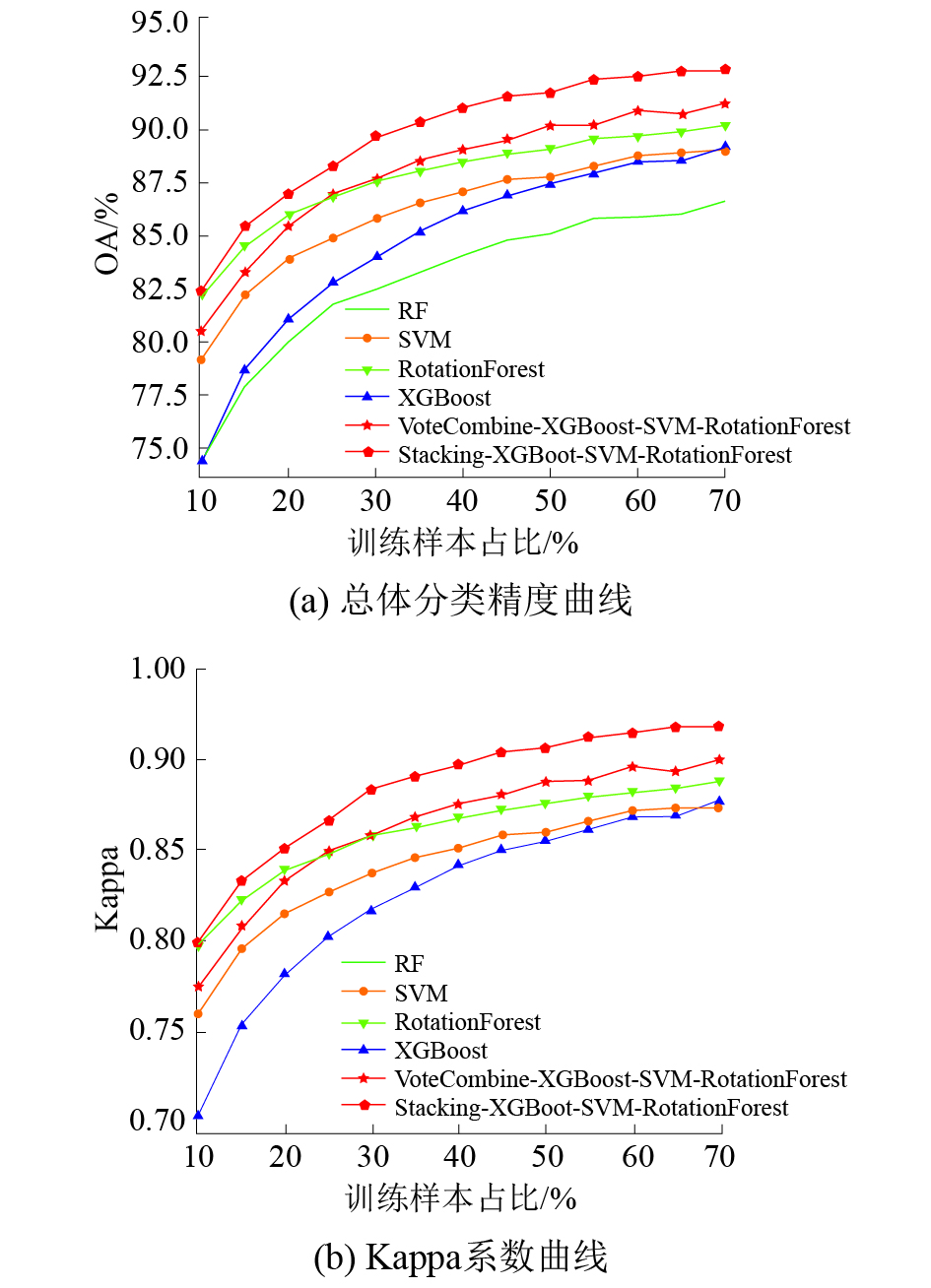
3.2 实验结果分析

实验结果如图2所示，其中VoteCombine-XGBoost-SVM-RotationForest表示使用投票机制的集成分类器曲线，其中3个分类器分别是XGBoost、SVM和RotationForest。当3个分类器判断不一致时，采用XGBoost当做主分类器。Stacking-XGBoost-SVM-RotationForest表示Stacking算法，其中3个level-0分类器即基础分类器分别是XGBoost、SVM和RotationForest，本次试验采用SVM为Meta分类器。

从图2中可以明显看出，XGBoost算法的表现效果要比RF要更出色。在训练集为10%时，两者保持相同的水准；当训练集开始上升，XGBoost和RF表现效果开始出现巨大差异；当训练集占比到达50%时，XGBoost已经领先RF的OA达到2.4%；在训练样本占比到70%时，OA差距扩大到2.65%。XGBoost算法虽然在训练样本较少的前期效果不及SVM和RotationForest，但是当训练样本占比超过50%，XGBoost和SVM几乎持平；在70%训练样本的情况下还稍领先于SVM，这足以显示XGBoost在高光谱图像分类中的适用性。而RotationForest在单一算法中始终保持着领先的优势，甚至在较低训练样本的情况下好于投票的MCS系统；在25%的训练样本情况下，RotationForest在OA上领先XGBoost、RF和SVM分别为3.85%、5.13%和1.87%，可见RoationForest优异的分类效果。从单一分类器的效果进行分析，在较少训练样本情况下，SVM和Rotation-Forest具有更强的泛化性能及更好的分类效果，随着训练样本的增多，XGBoost的分类效果提升最大，最后与SVM保持相近的分类效果。而RF在众多优异的分类器比较中，性能较差，所以在将RF分类加入MCS系统和Stacking系统会存在一些问题。

对投票的MCS和Stacking Learning进行比较，两者使用的分类器种类保持一致、参数保持一致，Stacking Learning从10%的训练样本起就领先于基于投票的MCS。在表1中70%训练样本时，Stacking Learning相较于MCS，OA增幅1.6%，AA增幅4.74%，Kappa增幅0.018 4。对于最优的传统的单一算法RotationForest，OA增幅2.67%，AA增幅4.97%，Kappa增幅0.030 8，Stacking Learning在各个训练样本阶段都表现出了优秀的稳定性。

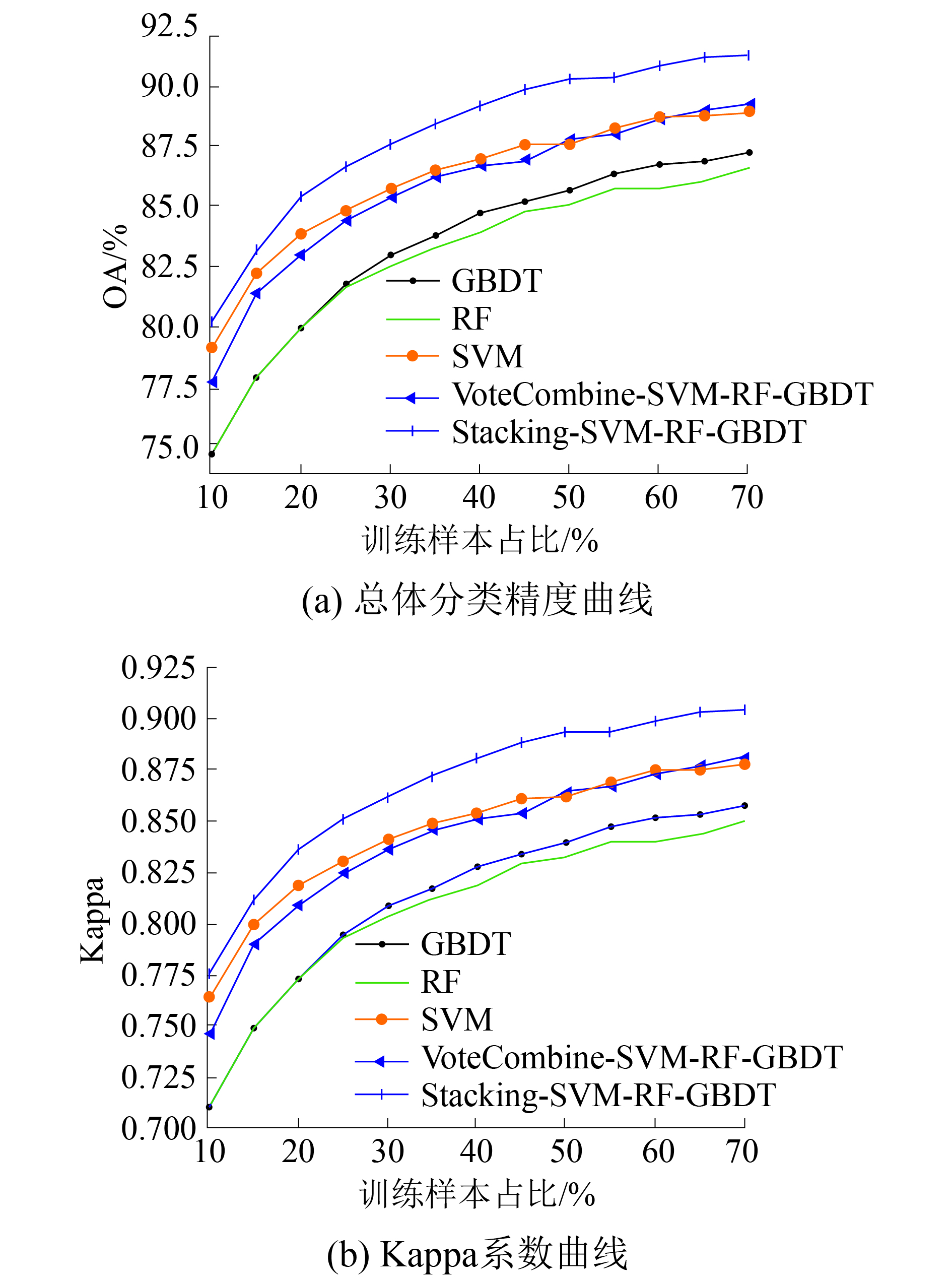
当使用的基础分类器分类效果参差不齐时，基于投票的MCS形成的判断决策会收到较大的影响，即集成效果可能弱于基础分类器。以OA为例，如图3所示，使用RF、GBDT和SVM组成分类器时，集成的效果并没有得到提升，甚至低于SVM，其原因可能在于2个较差效果的同质化分类器会严重影响到集成规则中的投票机制，解决方案是使用差异化模型或者分类决策更好的分类器，如图2中所示的分类器的组成形式。而使用Stacking Learning的方式进行集成，效果没有受限于分类器的种类和效果差异，依旧表现出色。分析原因可能在于Stacking Learning使用后验概率作为为Level-1的新特征，这些特征包含了判决时对样本各类的估计值，相较于单纯输出单个判决类别进行投票判决的MCS，更具有信息量，之后再使用强分类器对新的特征进行二次训练。整个过程可以认为是一种高效率的“降维”操作，即将原高光谱图像的数百个波段进行特征变换，得到由类后验概率构成的新特征。

4 结论

本文主要研究了新型分类器XGBoost对高光谱图像的适应性，并对Stacking Learning及MCS在各个样本情况下进行了对比实验。根据实验结果，得出以下结论：

1） XGBoost能够在高光谱图像中表现出较好的性能，相较于随机森林有更好的表现。对于小样本阶段，XGBoost无法发挥其最好的性能，弱于SVM；但当样本达到一定量级，XGBoost能获得与SVM相近的性能。

2） Stacking Learning一样适用于高光谱图像分类中，且具有较好的分类效果。相比较传统的基于投票的MCS，Stacking Learning并非十分依赖于基础分类器的结构与分类性能，而传统的MCS更适用于具有较强差异性且分类效果近似的分类器组合，对于同质化的分类器集成，MCS有时并不能提升分类效果，而Stacking Learning表现出了其独特的优势。

在日后的研究中可以将Stacking Learning的基础分类器进行并行计算，为更大程度地降低计算时间，可以考虑使用集群计算方式进行机器学习。