杆状一维构件在工业建筑中应用很广。在这些杆状构件的生产过程中,这类构件主要起承重作用,面临的压力较大,如果存在瑕疵很容易破损,酿成事故。检测过程不能对结构体造成损坏,因此对杆状构件进行无损检测就具有重要意义[1]。
时间反转法从光学中的相位共轭演变而来[2],能实现先到的信号后发,后到的信号先发。由于各信号能够同时同相到达目标位置,实现时间与空间上的聚焦,此项技术可以在不损坏被测物体的基础上实现无损检测。我国关于时反的研究取得了极具价值的研究成果。中科院声学研究所的汪承灏院士等[3]对各种介质下的时反进行了研究,证明其聚焦能力。汪承灏、魏炜等[4]对固体时反进行了科研,验证了时反抑噪能力与固体介质中的聚焦能力。邓菲等[5]率先进行了先进性的管道聚焦实验。
本文提出了基于小波包分析的时间反转聚焦算法的改进算法,在噪声的情况下,有效地分离出奇异点,实现损伤信号的聚焦和重构,并能提高监测系统的信噪比。
1 小波去噪含噪信号分解后[6],信号和噪声的小波系数的幅值将会不同。通过阈值的设定可以实现对噪声和信号的分离。小于阈值的系数去除,大于阈值的系数保留,所保留的即为去噪后小波系数。将保留下来的的有用信号的小波系数进行重构,即可获得去噪后的信号。
假设有如下观测信号:
| $f\left( t \right) = s\left( t \right) + n\left( t \right)$ |
式中:
现有一维信号
| ${w_f}\left( {j,k} \right) = {2^{\frac{j}{2}}}\sum\limits_{n = 0}^{N - 1} {f\left( n \right)} \psi \left( {{2^j}n - k} \right)$ |
在实际应用中,通过双尺度变换得到递归方程。
| $\begin{array}{*{20}{c}} {{s_f}\left( {j + 1,k} \right) = {s_f}\left( {j,k} \right) {\cdot} h\left( {j,k} \right)} \\ {{w_f}\left( {j + 1,k} \right) = {s_f}\left( {j,k} \right) {\cdot} g\left( {j,k} \right)} \end{array}$ |
式中:
| $\begin{gathered} {S_f}\left( {j - 1,k} \right) = {S_f}\left( {j,k} \right) {\cdot} {\overset{\frown} h} \left( {j,k} \right) + {w_f}\left( {j,k} \right){\cdot}{\overset{\frown} g} \left( {j,k} \right) \\ \end{gathered} $ |
当混有白噪声时:
| ${\omega _{j,k}} = {u_{j,k}} + {v_{j,k}}$ |
阈值的选择[7]:
| $T = \sigma \sqrt {2\ln n} /\exp (\left( {l - 1} \right)/2)$ |
阈值函数的选择:
| ${{\overset{\frown} \omega} _{j,k}} = \left\{ {\begin{array}{*{20}{c}} {{\omega _{j,k}} + T - \displaystyle\frac{{2T}}{{\exp \left( {\left| {\displaystyle\frac{{{\omega _{j,k}}}}{T}} \right| - 1} \right) + 1 + n}}},\;\;{{\omega _{j,k}} \leqslant - T} \\ {\displaystyle\frac{{2\operatorname{sgn} \left( {{\omega _{j,k}}} \right){{\left| {{\omega _{j,k}}} \right|}^{n + 1}}}}{{\left[ {\exp \left( {\left| {\displaystyle\frac{{{\omega _{j,k}}}}{T}} \right| - 1} \right) + 1 + n} \right]{T^n}}}},\;\;{\left| {{\omega _{j,k}}} \right| < T} \quad\quad\quad\\ {{\omega _{j,k}} - T + \displaystyle\frac{{2T}}{{\exp \left( {\left| {\displaystyle\frac{{{\omega _{j,k}}}}{T}} \right| - 1} \right) + 1 + n}}},\;\;{{\omega _{j,k}} \geqslant T} \end{array}} \right.$ |
小波阈值去噪的基本步骤如下:
1)利用小波变换分解含噪信号
2)用阈值处理小波系数
3)用小波逆变换对
对小波重构信号
按二进制细分频域中的
| $\left\{ {\begin{array}{*{20}{c}} \begin{gathered} M_j^0 = {V_j} \\ M_j^1 = {W_j} \\ \end{gathered} &({j \in {\bf Z}} )\end{array}} \right.$ |
则Hilbert空间的正交分解
| $\begin{array}{*{20}{c}} {M_{j + 1}^0 = M_j^0 \oplus M_j^1}&({j \in {\bf Z}}) \end{array}$ |
若
| $\left\{ {\begin{array}{*{20}{c}} {{m_{2n}}\left( t \right) = \sqrt 2 \displaystyle\sum\limits_{k \in Z} {h\left( k \right)} {m_n}\left( {2t - k} \right)} \\ {{m_{2n + 1}}\left( t \right) = \sqrt 2 \displaystyle\sum\limits_{k \in Z} {g\left( k \right)} {m_n}\left( {2t - k} \right)} \end{array}} \right.$ | (1) |
式中
| $\left\{ {\begin{array}{*{20}{c}} {{m_0}\left( t \right) = \displaystyle\sum\limits_{k \in Z} {{h_k}} {m_0}\left( {2t - k} \right)} \\ {{m_1}\left( t \right) = \sqrt 2 \displaystyle\sum\limits_{k \in Z} {{g_k}} {m_0}\left( {2t - k} \right)} \end{array}} \right.$ | (2) |
在多分辨率分析中
| $\left\{ {\begin{array}{*{20}{c}} {\varphi \left( t \right) = \displaystyle\sum\limits_{k \in Z} {{h_k}\varphi \left( {2t - k} \right),{{\left\{ {{h_k}} \right\}}_{k \in Z}}} \in {l^2}} \\ {\psi \left( t \right) = \displaystyle\sum\limits_{k \in Z} {{g_k}\varphi \left( {2t - k} \right),{{\left\{ {{g_k}} \right\}}_{k \in Z}}} \in {l^2}} \end{array}} \right.$ | (3) |
二者联立即可将
| $M_{j + 1}^n = M_j^n \oplus M_j^{2n + 1}(j \in {\bf Z},n \in {{\bf Z}_ + })$ |
小波包重构:
| $g_j^n\left( t \right) \in M_j^n,g_j^n\left( t \right) = \sum\limits_l {d_l^{j,n}} {m_n}\left( {{2^j}t - l} \right)。$ |
随机噪声设为
| $h\left( t \right) = \sum\limits_{i = 1}^\infty {{A_i}} \left( {t - {\tau _i}} \right)$ |
则根据声互易性原理[9],因为模型中激励元与接收元在同端,用信号处理技术模拟信号的接收(即被动时间反转技术)[10]。首波
| $y\left( t \right) = {r_c}s\left( t \right) \text{·} h\left( t \right) + n\left( t \right)$ | (4) |
将式(4)时反后再次发射,第2次接收的信号可表示为
| $y\left( t \right) = {r_c}s\left( t \right)\cdot h\left( t \right) \cdot h\left( t \right) + n\left( t \right)$ | (5) |
将式(5)时反后再次发射,第二次接收的信号可表示为
| $y\left( t \right) = {r_c}y\left( { - t} \right) \cdot h\left( t \right) \cdot h\left( t \right) + n\left( t \right)$ | (6) |
对式(6)作傅里叶变换得到
| $\begin{aligned} z\left( \omega \right) =& {r_c}{Y^ * }\left( \omega \right)H\left( \omega \right)H\left( \omega \right) + N\left( \omega \right) = \\ & r_c^2 \cdot X \cdot \left( \omega \right){\left| {H\left( \omega \right)} \right|^4} + r_c^2{N^ * }\left( \omega \right){\left| {H\left( \omega \right)} \right|^2} + N\left( \omega \right) \\ \end{aligned} $ | (7) |
式(7)可推导出
利用小波阈值去噪算法和小波包分解算法增强与时间反转算法相结合,增强了时间反转算法对桩基损伤的定位效果以及聚焦抑噪效果,具体的过程如下:
1)在symN小波基上对检测信号
2)小波重构,获得去噪信号
3)对去噪后的信号
4)桩基应力波检测信号数据和激励信号的函数表达都是已经确定的,分别为
| $H\left( \omega \right) = Y\left( \omega \right)/X\left( \omega \right)$ |
5)用宽度为
6)将每个截取信号
含噪信号经过小波包分解后,奇异点难以分辨;经过小波去噪后,使得奇异点容易分辨,有利于时间反转镜对损伤信号的聚焦,新的时反算法不但可以更好地识别损伤信号,而且使信号检测系统的信噪比有了进一步的提高。
5 实验与仿真单音频信号为幅值
| $s\left( t \right) = A \cdot \sin \left( {\omega t} \right)$ |
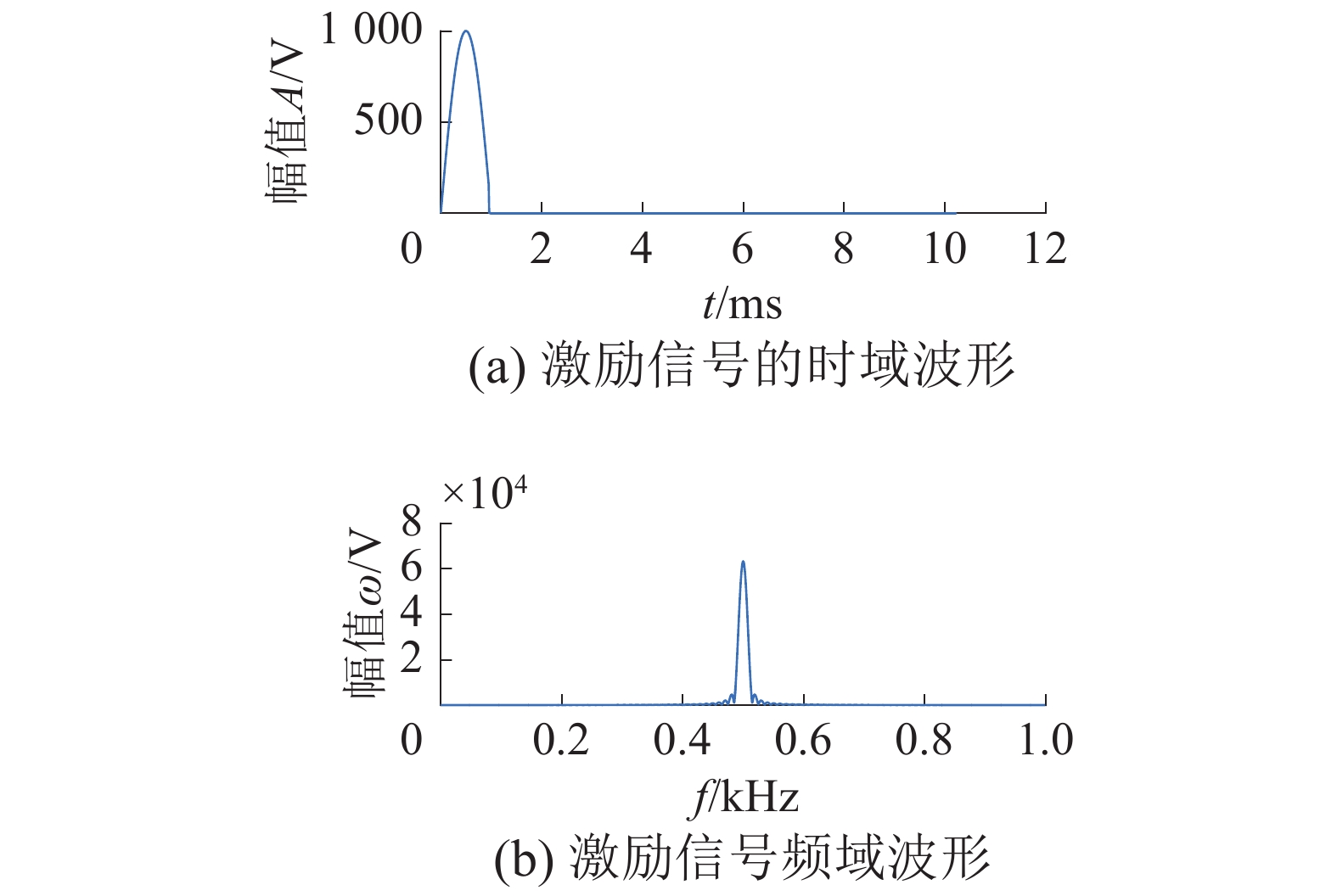
|
Download:
|
| 图 1 激励信号时域和频域波形 | |

|
Download:
|
| 图 2 桩基回波信号波形 | |
在图2中
对检测信号进行3层sym6小波包分解,得到如图3所示的子波,图中完整低信号区间为
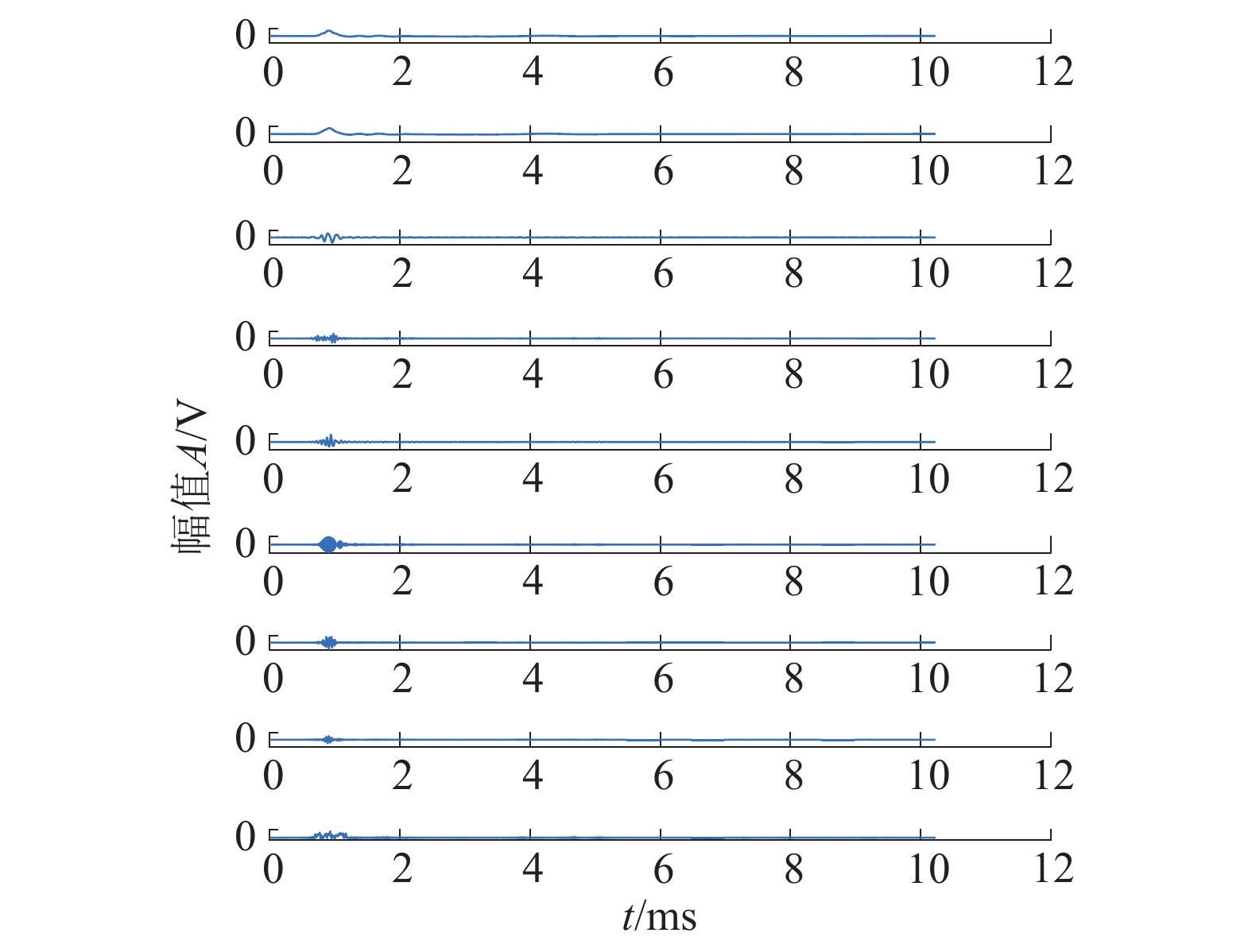
|
Download:
|
| 图 3 无噪回波信号小波包分解后的接收信号 | |
截取的损伤信号如图4所示。将yc1W~yc7W分别在时反窗内进行时间反转,为了更好地研究检测信号,利用时间反转算法进一步增强损伤回波信号。激励信号与首次回波信号已知,分别为
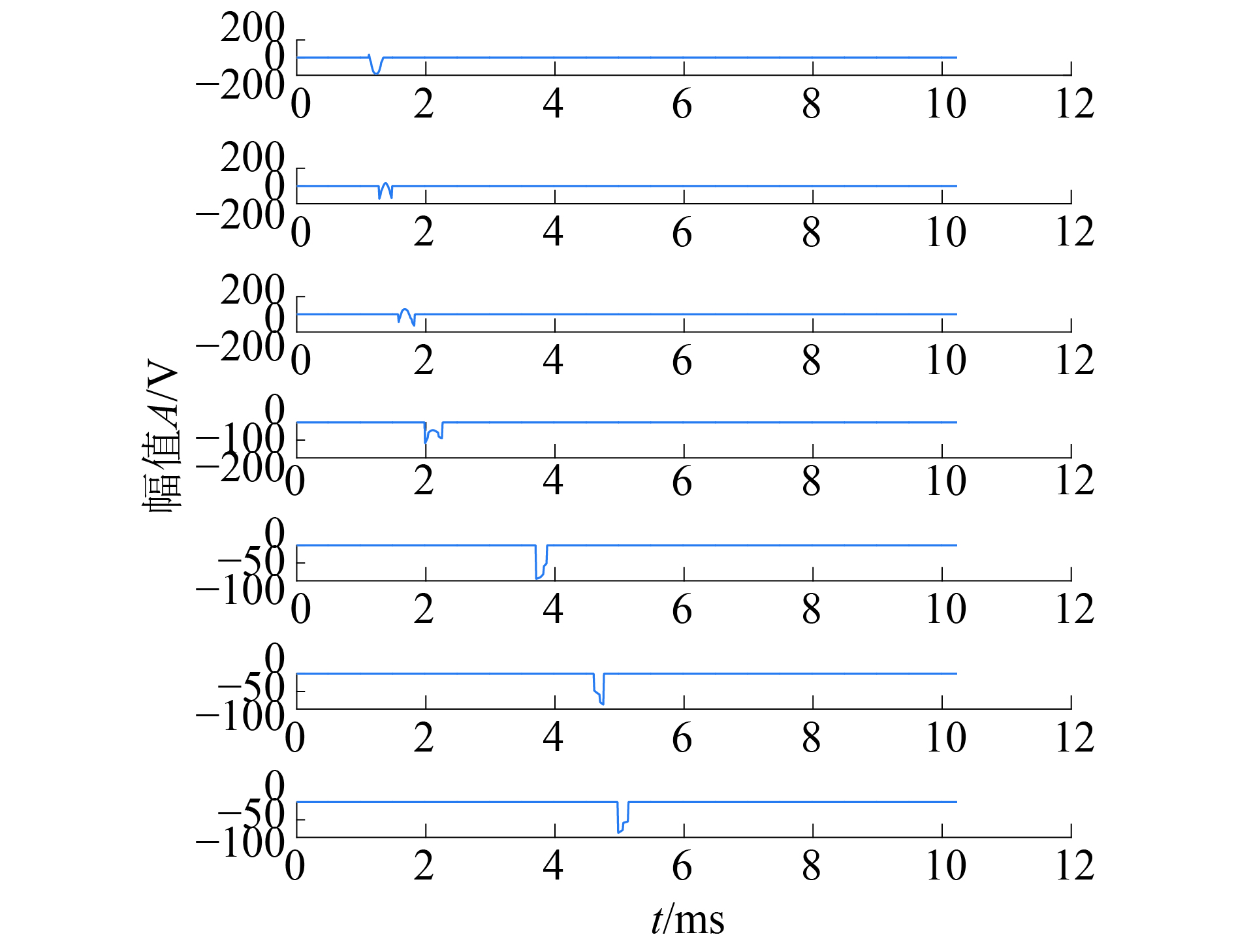
|
Download:
|
| 图 4 无噪回波信号截取的损伤信号 | |

|
Download:
|
| 图 5 无噪损伤信号聚焦信号 | |
|
|
表 1 无噪损伤信号聚焦增益 |
由表1可知,表中7处无噪损伤信号聚焦增益的平均值为18.496 6 dB。
当信号加入−0.67 dB高斯白噪声是时,首次回波信号为
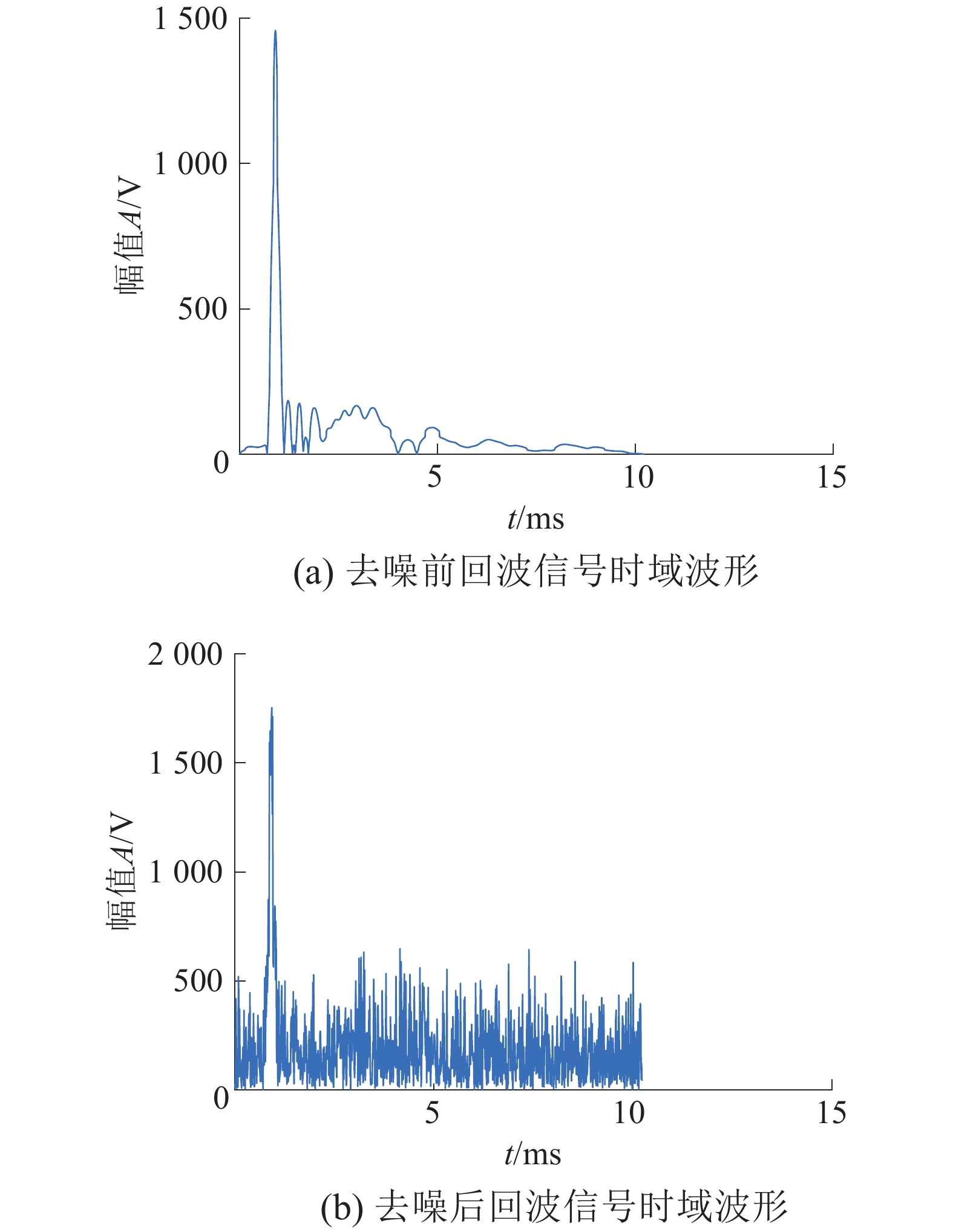
|
Download:
|
| 图 6 | |

|
Download:
|
| 图 6 加噪后回波信号 | |
对

|
Download:
|
| 图 7 小波分解后加噪回波信号 | |

|
Download:
|
| 图 8 截取的加噪信号 | |

|
Download:
|
| 图 9 小波去噪后小波分解回波信号 | |
从去噪后小波分解的回波信号中,可以更有效地分辨出奇异点,对奇异点进行截取,信道传递函数仍为

|
Download:
|
| 图 10 小波去噪后截取的回波信号 | |
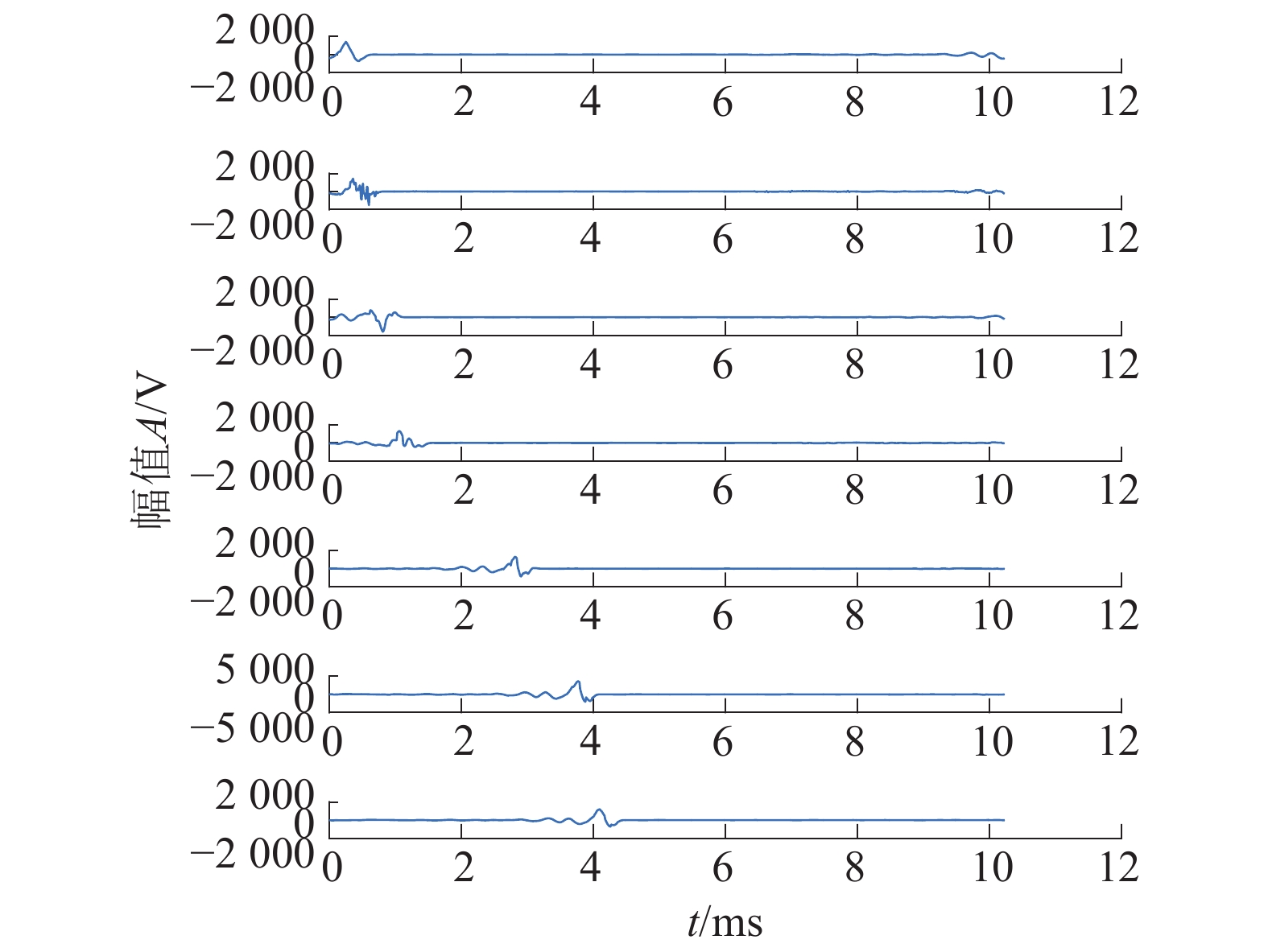
|
Download:
|
| 图 11 小波去噪后的损伤信号聚焦信号 | |
|
|
表 2 损伤点不同处理过程的信噪对比表 |
经计算,
从以上实验结果可以得出如下结论:
1)本文基于小波分析的时间反转改进算法,可以在含有噪声的情况下,识别出损伤点;
2)可以对损伤信号在损伤点处进行聚焦,并具有更强的抑制噪声能力,对损伤信号的信噪比平均提升了9.4 dB;
3)对每个损伤点都具有聚焦、抑制噪声和提高信噪比的能力,改进算法可以对一维构件实测中损伤的模式识别与定位以及信号的处理有一定的益处。
今后可以利用迭代算法进一步提升系统的信噪比以及聚焦增益。
| [1] |
高爽. 基于时间反转的杆状构件检测信号处理方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
( 0) 0)
|
| [2] |
范迪. 沉渣厚度超声检测信号处理技术研究及应用[D]. 青岛: 山东科技大学, 2010.
( 0) 0)
|
| [3] |
陆铭慧, 张碧星, 汪承灏. 各向异性单晶硅中声波时间反转自适应聚焦[C]//中国声学学会2003年青年学术会议[CYCA'03]论文集. 济南, 中国: 中国声学学会, 2003.
( 0) 0)
|
| [4] |
魏炜, 汪承灏. 有平界面存在时时间反转法的自聚焦性能[J]. 应用声学, 1999, 18(3): 1-5. DOI:10.3969/j.issn.1000-310X.1999.03.001 ( 0) 0)
|
| [5] |
邓菲, 吴斌, 何存富. 基于时间反转的管道导波缺陷参数辨识方法[J]. 机械工程学报, 2010, 46(8): 18-24. ( 0) 0)
|
| [6] |
徐洪, 陈正华, 周廷强, 等. 基于小波分解的岩石破坏次声信息特征研究[J]. 应用声学, 2016, 35(3): 231-238. ( 0) 0)
|
| [7] |
张磊, 杨媛, 李文涛, 等. 一种新的超声导波信号小波阈值去噪方法[J]. 西安理工大学学报, 2015, 31(3): 322-327. DOI:10.3969/j.issn.1006-4710.2015.03.013 ( 0) 0)
|
| [8] |
杨鑫蕊. 改进的小波阈值去噪算法研究[D]. 哈尔滨: 哈尔滨理工大学, 2014.
( 0) 0)
|
| [9] |
罗旌胜. 基于时间反转镜的聚焦方法及其应用研究[D]. 成都: 电子科技大学, 2013.
( 0) 0)
|
| [10] |
韩笑, 殷敬伟, 于歌, 等. 时变信道下的被动时间反转水声通信技术研究[C]//2016全国声学学术会议论文集. 武汉, 中国: 中国声学学会, 2016.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


