随着石油等化石能源的日益枯竭和环境污染问题的日益突出，风力发电等分布式电源和可入网电动汽车等主动负荷接入电网的比例不断提高。分布式电源具有的可靠、经济、灵活、环保等特点，有利于缓解能源紧缺和环境污染问题。然而，分布式电源地理位置分散，单机容量较小且具有显著的随机性、波动性和不确定性，直接接入电网会对电网的安全稳定产生极大的冲击^[1-3]。可入网电动汽车接入电网会产生新一轮负荷增长，加剧电网负荷峰谷差，增加了电网运行控制的难度。

虚拟电厂（VPP）^[4-5]的提出为分布式电源和主动负荷等接入电网提供了新思路。VPP在不改变电网现有拓扑结构的前提下，控制协调中心基于发电预测、负荷预测，通过先进的协调控制技术、智能计量技术和信息通信技术聚合分布式电源、可入网电动汽车、储能系统等不同类型的元件，通过上层的软件算法实现多分布式能源的协调优化运行，从而促进资源合理优化配置及利用。

目前就VPP的优化竞标问题，国内外学者已经做了许多开创性的研究工作。文献[5-6]以能量市场和旋转备用市场为背景，研究了VPP计及网络安全的竞标模型。文献[7]研究了一种基于双层模糊机会约束规划的VPP优化调度模型，优化模型中考虑到分布式新能源发电和负荷的不确定性。文献[8]研究了一种基于分时电价的VPP经济调度模型，分析了不同类型分布式电源出力系数和预测误差对其经济性的影响。文献[9]对VPP的一种具体实现形式即能效电厂进行综述。文献[10]在混合电力市场背景下研究了VPP竞标模型，模型中采用鲁棒优化法处理分布式电源出力的不确定性。

VPP参与市场竞标时，市场电价直接影响VPP的竞标行为，同时市场电价具有显著的不确定性，因此计及市场电价不确定性的VPP竞标问题值得深入研究^[11]。基于上述分析，本文采用鲁棒优化法处理市场电价的不确定性，同时基于EEMD-RVM实现市场电价的区间预测。算例分析证明提出的VPP竞标模型的有效性和实用性。

1 基于EEMD-RVM的区间预测

当前，传统预测方法多为点预测，其预测结果一般有不同程度的误差，难以满足电力系统安全稳定运行的实际需求。概率性区间预测方法可以将由不确定性因素引起的预测结果变动进行量化，在某一置信水平下使得实际观测值将落在由区间上、下界确定的预测区间（prediction intervals，PIs）内，向决策者提供更多的信息用于电力系统规划。本文基于EEMD-RVM模型实现不确定性参数的区间预测^[12]。

经验模态分解（empirical mode decomposition，EMD）是一种高效的信号分解方法，通过EMD可以将任意信号中不同尺度的波形或趋势逐级分解出来，得出一个剩余分量（residual，RES）和一系列的特征模态函数分量（intrinsic mode function，IMF）。集合经验模态分解在EMD的基础上加入高斯白噪声，同时进行多次EMD分解，最终将多次分解得出的IMF总体平均定义为最终的IMF，可有效避免EMD分解过程中由于IMF的不连续性而导致的混叠现象。

对于给定的训练样本 $\left\{ {{{{x}}_n},{{{t}}_n}} \right\}_{n = 1}^N$ ，其中 ${{x}}$ 为N维输入向量，t为标量输出，N为样本数量，RVM回归模型可定义为

${t_i} = y({x_i},{{w}}) + {\varepsilon _i}$

式中： ${{w}}{\rm{ = }}{({w_0},{w_1},...,{w_N})^{\rm{T}}}$ 为权值向量；样本噪声 ${\varepsilon _i}$ 服从 $N(0,{\sigma ^2})$ 的高斯分布，则RVM模型可表示为

${t_i} = \sum\limits_{i = 1}^N {{w_i}K} ({{x}},{x_i}) + {w_0} + \varepsilon $

式中： $K({{x}},{x_i})$ 为核函数， ${{x}}$ 为相关向量， $\varepsilon $ 为服从 $N(0,{\sigma ^2})$ 的独立样本误差。

通过最大似然方法可以得到超参数 ${{{\alpha }}_{{\rm{MP}}}}$ 和噪声方差 $\sigma _{{\rm{MP}}}^2$ 。RVM模型可以同时得出输入向量对应的预测均值和方差，分别为

$\left\{ \begin{array}{l}{y_*} = {t_*} = {{{\mu }}^{\rm{T}}}{{\varphi}} \left( {{x_*}} \right)\\\sigma _*^2 = \sigma _{{\rm{MP}}}^2 + {{\varphi}} {\left( {{x_*}} \right)^{\rm{T}}}{{\varSigma }}{{\varphi}} \left( {{x_*}} \right)\end{array} \right.$

式中： ${{\mu }}$ 为权值后验均值向量， ${{\varSigma }}$ 为后验协方差矩阵， ${{\varphi }}\left( {{x_i}} \right) = {\left( {1,K({x_1},{x_i}),K({x_2},{x_i}), \cdots ,K({x_N},{x_i})} \right)^{\rm{T}}}$ 。

因此，RVM模型能反映预测数据的不确定性，得到一定置信范围内的区间预测。在给定的置信度下，预测结果的置信区间可以表示为

$\left[ {{L_{\rm{b}}},{U_{\rm{b}}}} \right] = \left[ {{y_*} - {z_{{\alpha / 2}}}\sigma _*^{},{y_*} + {z_{{\alpha / 2}}}\sigma _*^{}} \right]$

式中： ${L_{\rm{b}}}{\text{、}}{U_{\rm{b}}}$ 为预测值的下（上）界， ${z_{{\alpha / 2}}}$ 为正态分布的双侧 $\alpha $ 分位数。

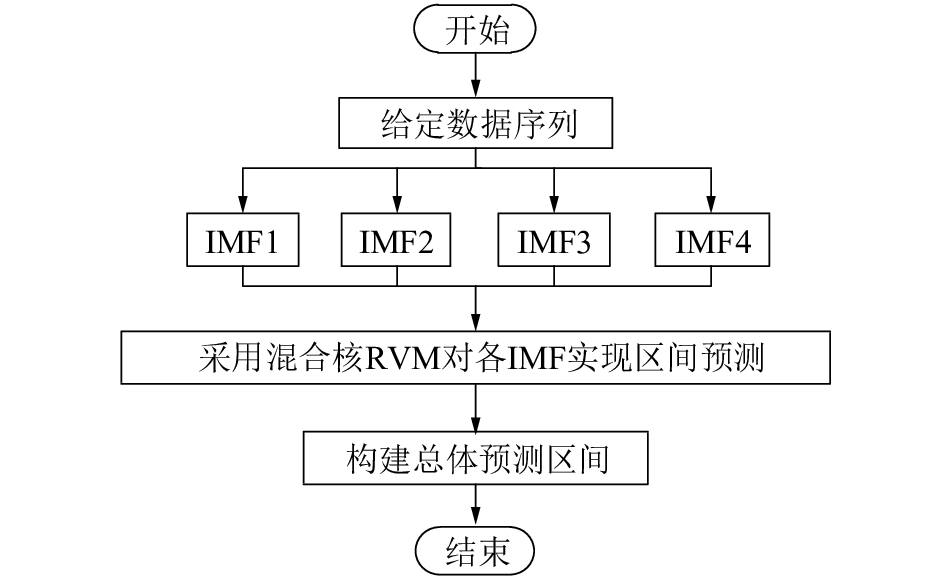
基于EEMD-RVM模型，首先采用EEMD方法将数据序列分解成多个IMF分量及RES分量，其次采用组合核RVM模型进行区间预测，具体实现步骤如图1所示。

2 VPP的竞标模型 2.1 目标函数

电网企业应尽量接受分布式电源出力，提高吸纳可再生能源发电的能力。本文考虑由小型风电场、燃气轮机、储能电池等构成VPP，VPP在最大限度接受风力发电的基础上，优化燃气轮机、储能电池的运行并参与日前市场竞标，实现竞标周期内系统经济效益最大。

$\max F = \sum\limits_{t = 1}^T {\left( {P_t^D\lambda _t^D - \sum\limits_{k \in {\rm{GSP}}} {{\alpha _k}\left\{ {{\lambda _t}} \right\}{P_{k,t}} - {C_t}} } \right)} $

(1)

${C_t} = \displaystyle\sum\limits_{i = 1}^{{N_i}} {\left( {{K_{i,t}}{k_i} + {p_i} + \sum\limits_{j = 1}^{{n_j}} {q_i^jg_{i,t}^j} } \right)}$

(2)

${P_{i,t}} = \displaystyle\sum\limits_{j = 1}^{{n_j}} {q_i^jg_{i,t}^j} $

(3)

式中：T为竞标周期；F为经济效益函数； ${P_t^D}$ 为t时刻内部负荷需求量； ${\lambda _t^D}$ 为t时刻负荷电价； ${\left\{ {{\lambda _t}} \right\}}$ 为t时刻市场电价；α_k为外部电网价格系数； ${{P_{k,t}}}$ 为竞标量（ ${{P_{k,t}}}$ 为正表示VPP从外部电网购电， ${{P_{k,t}}}$ 为负表示VPP向外部电网售电）；C_t为t时刻的成本；N_i为可分配发电机组数，0-1变量 ${{K_{t,i}}}$ 为t时刻机组i动作（启动或关闭）变量，为1时表示动作，为0时表示不动作；k_i为机组i的动作成本；将机组的二次成本函数分段线性化，n_j为分段数，p_i为固定成本， ${q_i^j}$ 为第j段的斜率， ${g_{i,t}^j}$ 为第j段的发电量， ${P_{i,t}}$ 为机组i的发电量。

2.2 约束条件

1）可控燃气轮机机组约束

$P_i^{\min }{v_{i,t}} \leqslant {P_{i,t}} \leqslant P_i^{\max }{v_{i,t}}$

(4)

$- r_i^{{\rm{down}}}\Delta t \leqslant {P_{i,t}} - {P_{i,t - 1}} \leqslant r_i^{{\rm{up}}}\Delta t$

(5)

${K_{i,t}} = \left| {{v_{i,t}} - {v_{i,t - 1}}} \right|$

(6)

${y_{i,t}} - {z_{i,t}} = {v_{i,t}} - {v_{i,t - 1}}$

(7)

${y_{i,t}} + {z_{i,t}} \leqslant 1$

(8)

${v_{i,t}} - {v_{i,t - 1}} \leqslant {v_{i,t + T{U_{i,w}}}}$

(9)

$T{U_{i,w}} = \left\{ \begin{array}{l}w,\;\;w \leqslant {\rm{MU}}{{\rm{T}}_i}\\0,\;\;\;w > {\rm{MU}}{{\rm{T}}_i}\end{array} \right.$

(10)

${v_{i,t - 1}} - {v_{i,t}} + {v_{i,t + T{D_{i,w}}}} \leqslant 1$

(11)

$T{D_{i,w}} = \left\{ \begin{array}{l}w,\;\;w \leqslant {\rm{MD}}{{\rm{T}}_i}\\0,\;\;\;w > {\rm{MD}}{{\rm{T}}_i}\end{array} \right.$

(12)

式中： $P_i^{\max }\left( {P_i^{\min }} \right)$ 为可控机组i输出功率的上（下）限， $r_i^{{\rm{up}}}\left( {r_i^{{\rm{down}}}} \right)$ 为可控机组i向上（下）爬坡速率，0-1变量 ${v_{i,t}}$ 为可控机组i状态变量，0-1变量 ${y_{i,t}}\left( {{z_{i,t}}} \right)$ 为可控机组i启（停）变量， ${\rm{MU}}{{\rm{T}}_i}\left( {{\rm{MD}}{{\rm{T}}_i}} \right)$ 为可控机组i最小启（停）时间，Δt为时段长度。

约束式（4）~（12）表示可控机组的出力、爬坡、启停及正常运行时的逻辑约束。

2）不可控风电机组约束

$P_t^{\rm{W}} \leqslant \left\{ {P_t^{{\rm{AW}}}} \right\}\\$

(13)

$P_t^{\rm{W}} \geqslant 0$

(14)

式中： $\left\{ {P_t^{{\rm{AW}}}} \right\}$ 为不可控风电机组输出功率的预测值。

3）输电线容量约束

${P_{k,t}} \!\!\! \geqslant \!\! - \min \left\{ {\max \left\{ {0,\left( {{P^{{\rm{D}},\max }} - \displaystyle\sum\limits_{i \in {\rm{DG}}} {P_i^{{\rm{DG}},\min }} - {{\left\{ {P_t^{{\rm{AW}}}} \right\}}^{\min }}} \right)} \right\},P_k^{{\rm{S}}\max }} \right\}$

(15)

${P_{k,t}}\!\!\! \leqslant \!\! \min \left\{ {\max \left\{ {0,\left( {\displaystyle\sum\limits_{i \in {\rm{DG}}} {P_i^{{\rm{DG}},\min }} \!\!+\!\! {{\left\{ {P_t^{{\rm{AW}}}} \right\}}^{\max }} \!\!+\!\! {e^{ \!\!-\!\! {\rm{ST}}}} - {P^{{\rm{D}},\min }}} \right)} \right\},P_k^{{\rm{S}}\max }} \right\}$

(16)

式中 $P_k^{{\rm{S}}\max }$ 为输电线最大容量限制。

4）功率平衡约束

$\sum\limits_i {{P_{i,t}}} + P_t^{\rm{W}} + \sum\limits_{k \in {\rm{GSP}}} {{P_{k,t}} + } P_t^{\rm{d}} = P_t^{\rm{D}} + P_t^{\rm{c}}$

(17)

2.3 计及不确定性的VPP竞标模型

上述竞标模型并未计及市场电价的不确定性，近年来，鲁棒优化已逐渐成为一种解决含不确定性变量问题的优化方法。鲁棒优化的核心思想是通过不确定集合描述不确定性变量，优化方案能够保证对于不确定集合内任意元素是可行的^[13-14]。采用鲁棒优化法处理市场电价的不确定性，计及不确定性的VPP竞标模型即

$\left\{ \begin{aligned}& \min G = \displaystyle\sum\limits_{t = 1}^T {\left[ {{C_t} + \displaystyle\frac{1}{2}\left( {{{\bar \lambda }_t} + {{\underline \lambda }_t}} \right)\sum\limits_{k \in {\rm{GSP}}} {{\alpha _k}{P_{k,t}} - P_t^{\rm{D}}\lambda _{_t}^{\rm{D}}} } \right]}+\\& \quad \quad \quad \varGamma v + \displaystyle\sum\limits_{t = 1}^T {{\eta _t}} \\& {\rm s}.{\rm t}.\;\;{\text{式}}\left( {2} \right)\sim \left( {17} \right)\\& \quad \quad \!\!\! v + {\eta _t} \geqslant \displaystyle\frac{1}{2}\left( {{{\bar \lambda }_t} + {{\underline \lambda }_t}} \right){y_t}\\& \quad\quad\!\!\! - {y_t} \leqslant \displaystyle\sum\limits_{k \in {\rm{GSP}}} {{\alpha _k}{P_{k,t}}} \leqslant {y_t}\\ & \quad\quad \!\! v,{\eta _t},{y_t} \geqslant 0\end{aligned} \right.$

式中：Γ为鲁棒系数； ${\overline \lambda _t}{\text{、}}\;{\underline \lambda _t}$ 为市场电价的上下限；v、η_t、y_t为对等转化中引入的辅助决策变量，无具体物理意义。

通过将鲁棒优化模型中不确定性变量的区间预测结果划分为不同的子区间，利用文献[15]建立的迭代算法可以得出VPP在竞标周期内各不同时段的最优竞标曲线。与现有VPP竞标模型单时段对应单一的功率值不同，本文得出的最优竞标曲线为价格—功率曲线，根据竞标曲线，VPP可以依据市场电价的变化修正竞标功率以实现竞标周期内的经济效益最大化^[16]。

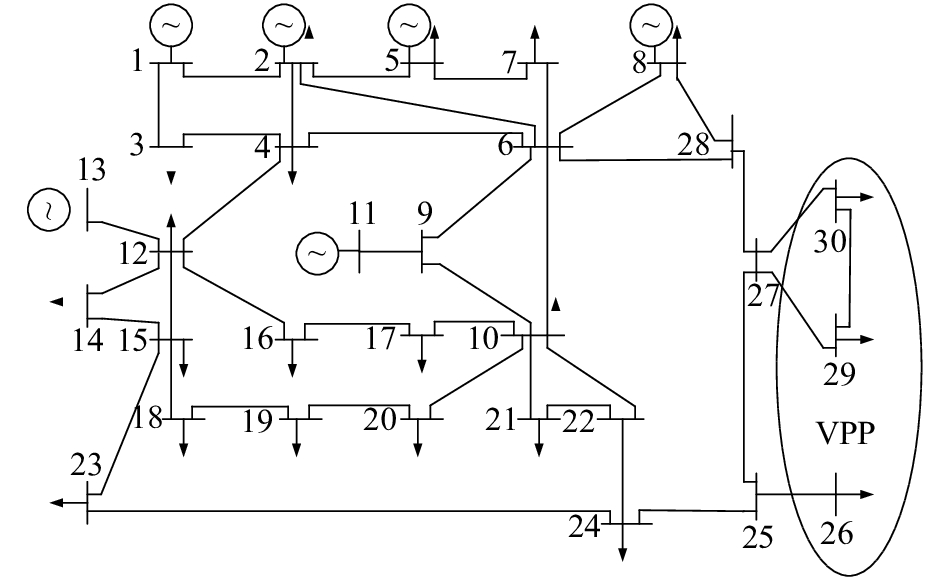
3 算例分析

为了验证本文提出的VPP竞标模型，算例选取IEEE30节点系统进行适当改进：节点26处接入2台燃气轮机，节点29处接入2台燃气轮机和1座风电场，节点30处接入一台储能电池，节点26/29/30共同组成一个VPP系统，如图2所示。

VPP竞标周期为1天，分为24个时段。VPP可通过节点26/29/30从外部电网购（售）电，假设各节点购（售）电价格为日前市场电价预测值的α_k倍，α_k取值为{0.95,1.0,1.05}。

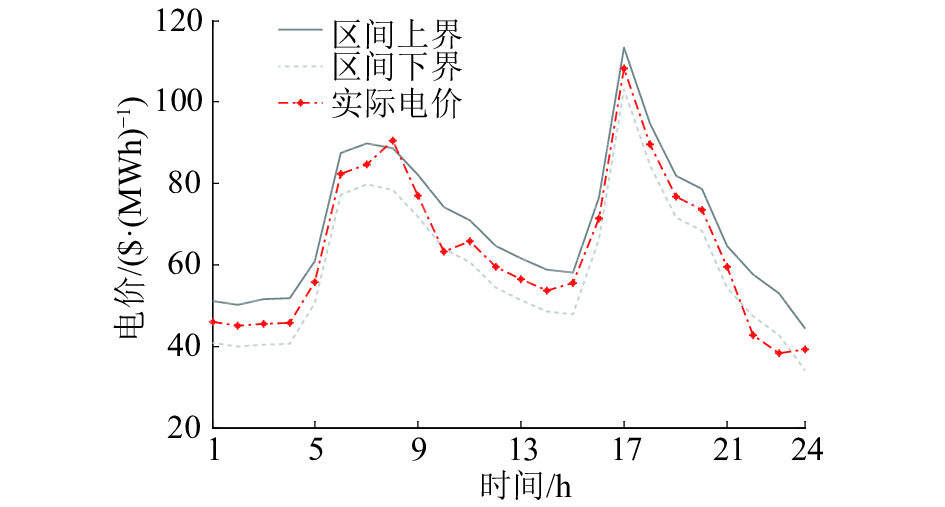
采用EEMD-RVM区间预测模型，基于欧洲电能交易中心EEX历史数据对风电出力和市场电价进行区间预测，区间预测结果及实际数据如图3所示。

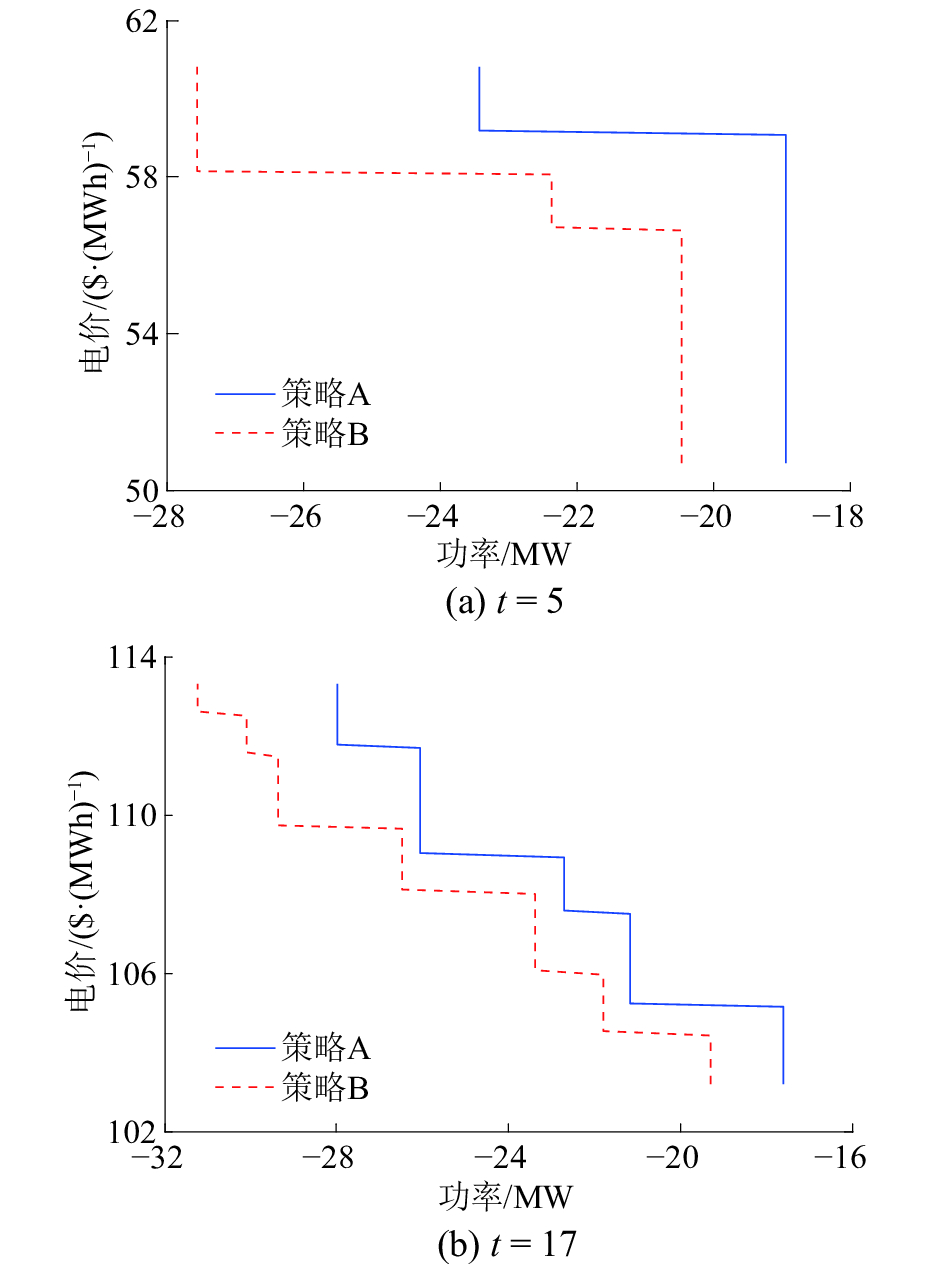
鲁棒优化中鲁棒系数越大，即认为预测值与实际值偏差越大，优化结果越保守。针对2种不同保守度的竞标策略进行分析比较，分别为：策略A：Γ=24；策略B：Γ=8。2种策略下t=5和t=17对应的最优竞标曲线如图4所示。

从图4中可以看出，对于相同的鲁棒系数Г，VPP更倾向于在t=17时段向外部电网售电。例如，对于策略A，t=5时段VPP的售电区间为[−23.4，−18.9] ，单位为MW，t=17时段VPP的售电区间为[−28.0，−17.6] ，单位为MW。这是因为t=17时段对应的市场电价高于t=5时段，VPP倾向于在高电价时段向外部电网售电以提高竞标效益。

由图4曲线可以看出，高电价时段竞标曲线覆盖的区间大于低电价时段。另一方面，在同一时段，随着鲁棒系数Г数值增大，最优竞标曲线向右移动，即采取较为保守的竞标策略会减小VPP向外部电网的售电量。例如，在t=5时段，策略A对应的鲁棒系数大于策略B。由图4可以看出，策略A对应的售电量小于策略B。这是因为，当鲁棒系数Г数值减小时，即认为市场电价的预测值与实际值偏差越小，VPP倾向于向外部电网售电。随着Г数值的增大，市场电价的预测值与实际值偏差越大，VPP减小向外部电网售电量。

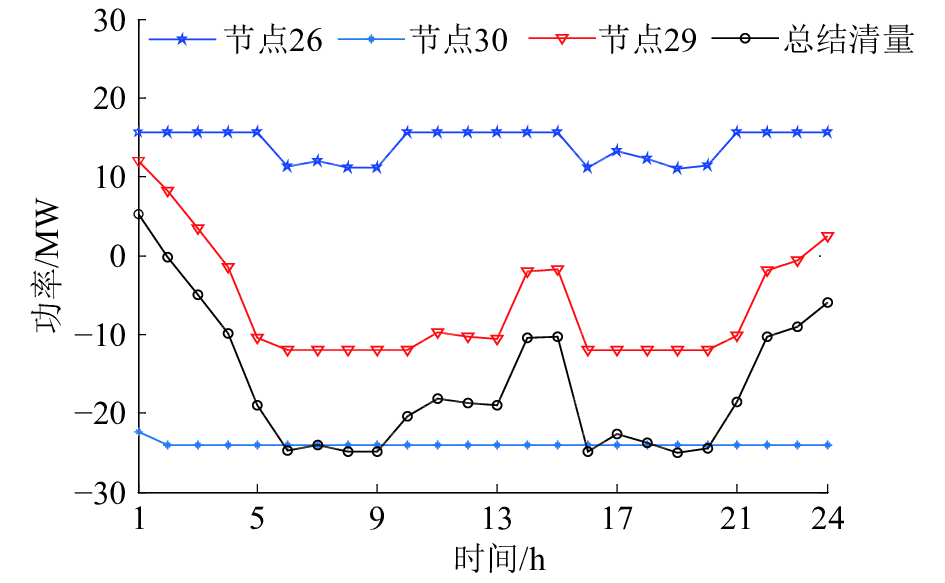
以图3中的实际电价进行市场结清，VPP中不同节点处的结清量如图5所示，从图5中可以看出，由于各节点购（售）电价格不同，VPP选择在节点26处从外部电网购电，在节点30处向外部电网售电。同时，为了满足VPP的功率平衡约束，在节点29处市场电价较低的时段从外部电网购电，剩余时段向外部电网售电。VPP通过协调内部可控分布式电源(distributed generation, DG)、不可控风电机组及负荷需求等优化运行，通过不同节点与外部电网联系，可以提高竞标经济效益。

4 结论

虚拟电厂通过灵活组合分布式电源、可控负荷和储能装置等可以实现分布式电源的互补，以“单一电厂”形式参与电力市场交易和向系统操作员提供辅助服务。市场电价的不确定性是VPP参与市场竞标时必须考虑的一个重要因素。

本文采用鲁棒优化法处理市场电价的不确定性，同时基于EEMD-RVM实现市场电价的区间预测，从而建立了VPP鲁棒优化竞标模型。算例分析了不同鲁棒系数对VPP竞标行为的影响，同时分析了不同节点电价对VPP与外部电网能量调配的影响。由分析结果得出如下结论：

1）VPP倾向于在高电价时段向外部电网售电以提高竞标效益。

2）当鲁棒系数减小时，即认为市场电价的预测值与实际值偏差越小，VPP倾向于向外部电网售电。

3）本文所提模型具有一定的有效性和实用性，可以实现VPP的优化竞标。