2. 江西理工大学 信息工程学院,江西 赣州 341000;
3. 哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001
2. School of Information Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
3. College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China
随着集成电路、微电子技术、无线通信、嵌入式和传感器技术的高速发展,传感器网络已经由20世纪70年代的第一代发展到了第四代,即无线传感器网络(WSN)[1]。尤其是进入21世纪后,无线传感器网络技术作为物联网的组成要素,已经被广泛应用于军事、环境监测、自然灾害预报、医疗健康、智能家居等众多领域[2]。无线传感器网络的部署可以通过飞行器散播、人工规划埋置等方式完成,部署完成后,各节点以自组织的形式构成网络。无线传感器网络系统通常由传感器节点(sensor node)、基站(base station, BS)和管理节点组成,其中,传感器节点由能量有限的不可充电电池提高电力[3]。无线传感器网络高度依赖于具体应用场景,受能源、存储容量和功率的限制,所以对于每个路由协议,减少能耗是延长网络寿命的重要考虑因素[4]。
自Heinzelman等[5]第一次提出了分层聚类的低功耗自适应集簇分层型协议(low energy adaptive clustering hierarchy,LEACH)协议后,由于其在延长无线传感器网络寿命方面具有优良的性能,此后,聚类协议开始受到研究学者的广泛关注。LEACH通过簇头轮换机制较好地平衡各节点的能耗,其在同构WSN中表现良好,但是在异构环境中的性能有所下降。文献[2]针对此问题进行优化,提出了在异构环境中适应性更强的DEEC协议。
在分层聚类协议中,WSN运作以轮为单位。由于LEACH类协议在每轮的簇头选举中通过预先计算一个阈值
大多数分层聚类协议为努力延长网络整体寿命而忽略了出现零簇头情况和WSN有效运行的阶段,不能避免出现零簇头的情况,也没能够有效地延长半数存活节点运作轮数,特别是稳定周期。因此,本文提出了基于簇头选举和节点位置优化的分层聚类协议(based on cluster election and position optimization clustering hierarchy, BCEPOCH)意在解决以上问题。BCEPOCH并不盲目追求WSN整体寿命,而是争取最长的稳定期和半数存活节点周期。同时,BCEPOCH可以保证每轮稳定地选举出最佳的簇头数量,避免零簇头轮的出现。
1 无线传感器网络模型 1.1 无线传感器结构在
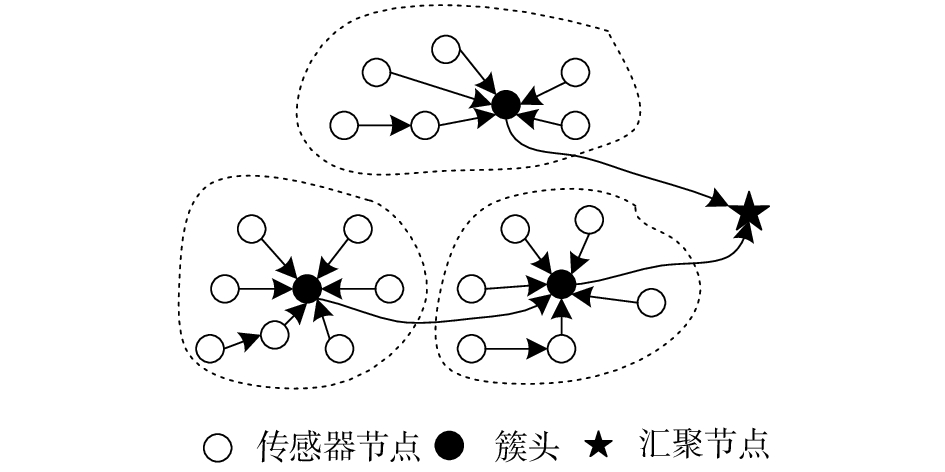
|
Download:
|
| 图 1 无线传感器网络示意 | |
本文采用文献[9]两级异构传感器,即普通传感器节点和高级传感器节点2种传感器。假设普通传感器节点的初始能量为
| $\begin{array}{l}{E_{{\rm{total}}}} = N\left( {1 - m} \right){E_0} + Nm\left( {1 + a} \right){E_0} = \\\;\;\;\;\;\;\;\;\;N{E_0}(1 + am)\end{array}$ | (1) |
从式(1)可以看出,在两级异构网络中,整个网络初始能量附加了am倍的能量,或者认为附加了am倍个传感器节点。
1.3 能量消耗模型分层无线传感器网络的能量消耗主要发生在数据传输阶段和簇头对数据的处理分析融合部分。由于无线电传输中的能量消耗通常远大于一般传感器操作和存储器访问的能耗,所以本文只考虑数据无线传输和数据融合部分的能量消耗,忽略数据存储和其他操作的能量消耗。发生数据传输的主要有3个部分:1)普通传感器节点采集数据发送到簇头部分;2)簇头接收传感器节点数据;3)簇头发送数据到Sink节点部分。所以,加上簇头处理数据所消耗的能量,本文计算WSN网络的能耗共计以上4个部分,采用文献[5, 10]的能量消耗模型,传感器节点发送和接收k-bit消息的能量消耗分别定义为
| ${E_{{\rm{Tx}}}}\left( {k,d} \right) = \left\{ {\begin{array}{*{20}{c}} {k{E_{{\rm{elec}}}} + k{E_{{\rm{fs}}}}{d^2},d < {d_0}} \\ {k{E_{{\rm{elec}}}} + k{E_{{\rm{amp}}}}{d^4},d \geqslant {d_0}} \end{array}} \right.$ |
| ${E_{{\rm{Rx}}}}\left( k \right) = k{E_{{\rm{elec}}}}$ |
| ${d_0} = \sqrt {\frac{{{E_{{\rm{fs}}}}}}{{{E_{{\rm{amp}}}}}}} $ |
| ${E_{{\rm{CH}}}} = \left\{ {\begin{array}{*{20}{c}} {k({E_{{\rm{elec}}}} + {E_{{\rm{DA}}}}) + k{E_{{\rm{fs}}}}{d^2},d < {d_0}} \\ {k({E_{{\rm{elec}}}} + {E_{{\rm{DA}}}}) + k{E_{{\rm{amp}}}}{d^4},d \geqslant {d_0}} \end{array}} \right.$ |
式中:
在文献[9-10]中都采用了由节点初始能量和当前节点剩余能量来确定簇头选举概率。设节点i在r轮中成为簇头的概率为
| ${p_i}\left( r \right) = \left\{ {\begin{aligned}& {\displaystyle\frac{{{P_{{\rm{opt}}}}{E_i}(r)}}{{(1 + a \times m)\overline {E} (r)}}{\rm{ }}, \;\; i{\text{是普通节点}}}\\& {\displaystyle\frac{{{P_{{\rm{opt}}}}(1 + a){E_i}(r)}}{{(1 + am)\overline {E}(r) }}{\rm{ }}, \;\; i{\text{是高级节点}}}\end{aligned}} \right.$ |
| ${P_{{\rm{opt}}}} = \sqrt {\frac{1}{{2N{\rm{\pi }}}}} \sqrt {\frac{{{E_{{\rm{fs}}}}}}{{{E_{{\rm{amp}}}}}}} \frac{M}{{d_{{\rm{toSink}}}^2}}$ |
式中:
| $\overline {E}(r) = \frac{{{E_{{\rm{total}}}}(1 - \displaystyle\frac{r}{R})}}{N}$ |
式中:R为网络寿命的总轮数,它也是通过预估得到,预估公式为
| ${E_{{\rm{round}}}} = l(2N{E_{{\rm{elec}}}} + N{E_{{\rm{DA}}}} + k{E_{{\rm{amp}}}}d_{{\rm{toSink}}}^4 + N{E_{{\rm{fs}}}}d_{{\rm{toCH}}}^2)$ |
式中:l是簇头数量,
Heinzelman等[5]定义了节点i的簇头阈值,本文遵循该阈值模型。节点i的阈值计算公式为
| $T\left( i \right) = \left\{ {\begin{split}&{\displaystyle\frac{{{p_i}\left( r \right)}}{{1 - {p_i}\left( r \right)(od (r,1/{p_i}\left( r \right)))}},i{\text{是候选簇头}}}\\&{0,{\text{其他}}}\end{split}} \right.$ |
在分层聚类算法中,每一个节点都用属性Gnode来标记该节点是否属于候选簇头集合G,当某一个节点在最近
我们假设在某轮中可以作为候选簇头节点(candidate cluster head,CCH)的数量为ncch,最佳簇头(optimal cluster head,OCH)数量为noch。在理想的情况下,每一轮的运行中都应该选出noch个簇头,在WSN网络运行前期未出现死亡节点时,可作为簇头的候选节点数量ncchcCH远大于最佳簇头数量为noch,这时可以通过节点阈值选举出nochoCH个簇头。随着节点死亡,候选簇头节点减少,当ncch=nochcCH=noCH时,为了保合理的簇头数量,跳过阈值选举将ncch个候选节点全部选举为簇头。随着节点死亡数量进一步增加,当ncch<nochcCH<noCH时,则无法选出最佳数量的簇头。出现这种情况时,更新未被选为簇头存活节点的Gnode值,不需要等待

|
Download:
|
| 图 2 BCEPOCH簇头选举流程 | |
根据式(1),我们得到了距离与无线电能耗的关系,如图3所示。显然,当节点距离越远时,无线传输所消耗的能量就越大,并且随着距离d的增加呈现指数级增长的趋势。所以,当节点到基站的距离大于
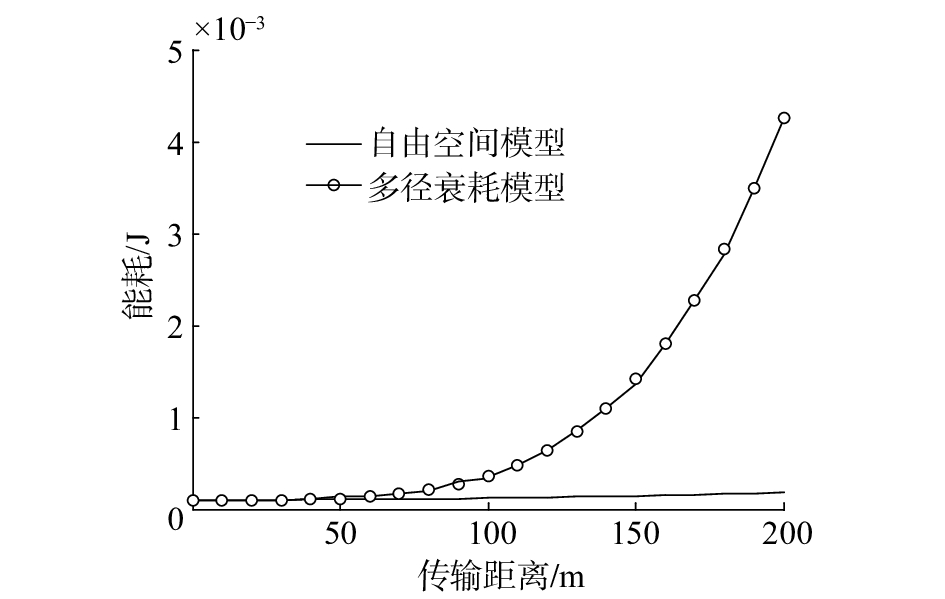
|
Download:
|
| 图 3 距离和能耗的关系 | |
选举簇头时本文同时兼顾节点与基站的距离和节点与簇头距离,当选举第一个簇头时只考虑节点与基站距离的影响,定义了修正因子
| $\varphi \left( {i,j} \right) = {\left( {\frac{{{s_{{\rm{avg\_to\_Sink}}}}}}{{{s_{{\rm{i\_to\_Sink}}}}(i)}}} \right)^\alpha }i \in \left[ {1,N} \right],j = 1$ |
| $T\left( i \right) = T\left( i \right)\varphi \left( {i,j} \right) = T\left( i \right){\left( {\frac{{{s_{{\rm{avg\_to\_Sink}}}}}}{{{s_{{\rm{i\_to\_Sink}}}}(i)}}} \right)^\alpha }$ |
式中:节点
根据式(2)选择出第一个簇头后,在第二个簇头选举前,根据节点与簇头1的距离和节点与基站的距离对阈值进行修正。计算如下:
| $\begin{array}{l}\varphi \left( {i,j} \right) = {\left( {\displaystyle\frac{{{s_{{\rm{i\_min\_to\_CH}}}}(j)}}{{{s_{{\rm{avg\_min\_to\_CH}}}}}}} \right)^\beta }{\left( {\displaystyle\frac{{{s_{{\rm{avg\_to\_Sink}}}}}}{{{s_{{\rm{i\_to\_Sink}}}}(i)}}} \right)^\alpha }\end{array}$ |
式中:
本文仿真环境使用MATLAB 8.1平台,在大小为100 m×100 m场地中随机部署100个传感器节点,其他具体实验参数如表1所示。与LEACH[5],TSEP[11],MODLEACH[13]协议作比较,分析BCEPOCH的性能。图4为BCEPOCH运行示意图。
|
|
表 1 实验参数 |
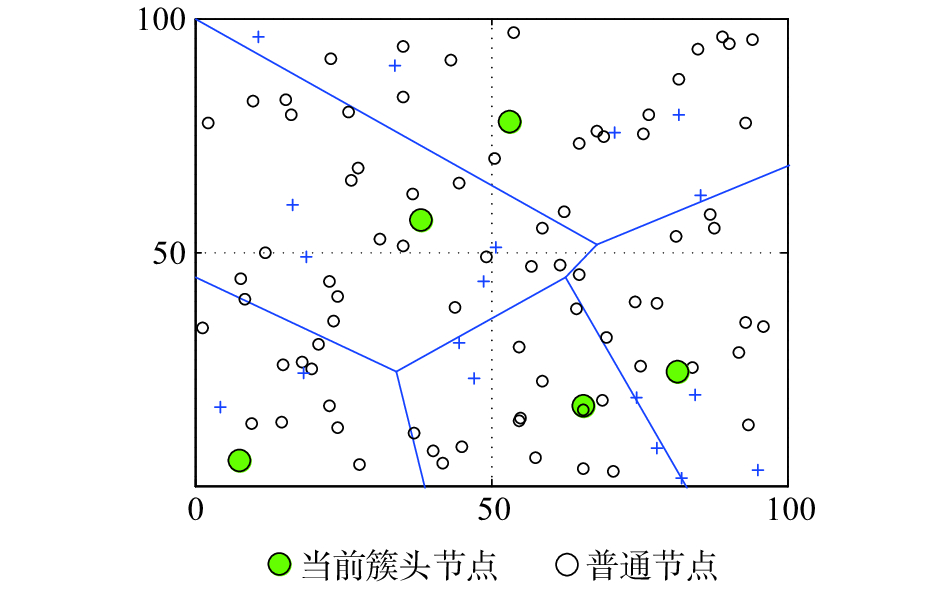
|
Download:
|
| 图 4 BCEPOCH运行示意 | |
本文算法针对LEACH、TSEP等算法在簇头选举时出现不稳定和零簇头的情况进行簇头选举优化,优化后保障WSN在稳定期内的簇头数量始终为
|
|
表 2 各算法簇头选举数量分析 |

|
Download:
|
| 图 5 簇头稳定性分析 | |
由表2和图5可以得出,在稳定期、半数存活节点期和整个网络生命周期本文提出的BCEPOCH算法在簇头选举的稳定性上明显高于其他算法。尤其在稳定期内没有节点死亡时,BCEPOCH每轮网络运行都能选举出5个最佳数量的簇头,并且在稳定期均值为5,方差为零,性能表现与理想情况相同,LEACH与MODLEACH表现几乎相同,TSEP表现最差。
3.2 网络有效生命周期和网络寿命本文算法在优化簇头选举的同时通过节点与基站的距离和节与簇头距离实时修正节点阈值,延长WSN网络的稳定期和半数存活节点时期。通过MATLAB仿真,得到各协议的在不同阶段的运作轮数,结果汇总如表3所示。
|
|
表 3 各协议不同阶段的运作轮数 |
分析表3数据可以得出,在网络的稳定期和半数存活节点时期内,本文提出的BCEPOCH算法网络运作轮数明显高于其他3种算法。在稳定期内运行轮数表现相比于LEACH、TSEP、MODLEACH分别提高了35.55%、22.85%、22.22%,在半数存活点时期分别提高了40.19%、14.30%、40.07%,在整个网络寿命周期内,BCEPOCH算法运作轮数少于其他3种算法。但是由于BCEPOCH稳定的簇头选举策略使得每一轮都可以选举出簇头,不会出零簇头情况,所以在整个网络寿命的有效轮数中BCEPOCH算法仍然优于其他3种算法,较其他3种算法分别提高了66.84%、47.53、136.91%。在图6中可以明显得出,BCEPOCH算法在有效地延长了WSN网络的稳定期和半数存活节点期的同时又延长了整体网络运行的有效轮数。

|
Download:
|
| 图 6 各时期网络寿命周期对比 | |
针对无线传感器网络中簇头选举的不稳定性和稳定期较短的问题进行研究,通过仿实验分析本文主要做出以下改进和展望:
1)提出的修改簇头选举流程可以有效地保障每轮网络都能选举出合理数量的簇头,避免零簇头的产生,提高簇头选举的稳定性。
2)根据节点与簇头的距离和节点与基站的距离实时修改节点阈值,延长网络的稳定期。
3)本文中仍然存在可以优化的空间,可以看出本文算法在稳定期与生命周期的占比上并不占优势,下一步的研究应当重点关注与提高稳定期的占比上。
| [1] |
王平, 王恒. 无线传感器网络技术及应用[M]. 北京: 人民邮电出版社, 2016: 3-8.
( 0) 0)
|
| [2] |
蔺莉, 张莉华. 无线传感器网络中能量高效的自适应分簇算法[J]. 仪表技术与传感器, 2017(3): 121-126. DOI:10.3969/j.issn.1002-1841.2017.03.031 ( 0) 0)
|
| [3] |
LI Qing, ZHU Qingxin, WANG Mingwen. Design of a distributed energy-efficient clustering algorithm for heterogeneous wireless sensor networks[J]. Computer communications, 2006, 29(12): 2230-2237. DOI:10.1016/j.comcom.2006.02.017 ( 0) 0)
|
| [4] |
YADAV R, SAXENA S. Improved leach routing protocol with soft computing[C]//Proceedings of the 2nd International Conference on Advances in Computing and Communication Engineering. Dehradun, India: IEEE, 2015: 261-266.
( 0) 0)
|
| [5] |
HEINZELMAN W B, CHANDRAKASAN A P, BALAKRISHNAN H. An application-specific protocol architecture for wireless microsensor networks[J]. IEEE transactions on wireless communications, 2002, 1(4): 660-670. DOI:10.1109/TWC.2002.804190 ( 0) 0)
|
| [6] |
MAO Lin, ZHANG Ying. An energy-efficient LEACH algorithm for wireless sensor networks[C]//Proceedings of the 36th Chinese Control Conference. Dalian, China: IEEE, 2017: 9005-9009.
( 0) 0)
|
| [7] |
李一泓. 基于能量异构无线传感器网络的路由算法研究[D]. 南昌: 南昌大学, 2013.
( 0) 0)
|
| [8] |
严英鹏. 基于混合聚类算法的无线传感器网络LEACH协议改进研究[D]. 广州: 华南农业大学, 2016.
( 0) 0)
|
| [9] |
LIU Jingjing, HU Yanjun. A balanced and energy-efficient clustering algorithm for heterogeneous wireless sensor networks[C]//Proceedings of the 6th International Conference on Wireless Communications and Signal Processing. Hefei, China: IEEE, 2014: 1-6.
( 0) 0)
|
| [10] |
GAO Ying, WKRAM C H, DUAN Jiajie, et al. A novel energy-aware distributed clustering algorithm for heterogeneous wireless sensor networks in the mobile environment[J]. Sensors, 2015, 15(12): 31108-31124. DOI:10.3390/s151229836 ( 0) 0)
|
| [11] |
KASHAF A, JAVAID N, KHAN Z A, et al. TSEP: threshold-sensitive stable election protocol for WSNs[C]//Proceedings of the 10th International Conference on Frontiers of Information Technology. Islamabad, India: IEEE, 2012: 164-168.
( 0) 0)
|
| [12] |
JAVAID N, QURESHI T N, KHAN A H, et al. EDDEEC: enhanced developed distributed energy-efficient clustering for heterogeneous wireless sensor networks[J]. Procedia computer science, 2013, 19: 914-919. DOI:10.1016/j.procs.2013.06.125 ( 0) 0)
|
| [13] |
TIWARI T, ROY N R. Modified DEEC: a varying power level based clustering technique for WSNs[C]//International Conference on Computer and Computational Sciences. Noida, India: IEEE, 2015: 170-176.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


