2. 黑龙江省农业科学院 遥感技术中心,黑龙江 哈尔滨 150086
2. Remote Sensing Technology Center, Heilongjiang Academy of Agricultural Sciences, Harbin 150086, China
高光谱图像处理技术应用前景广,具有很高的研究价值,但是由于高光谱图像数据维数高,波段之间相关性较高,具有较高的冗余度,导致高光谱图像处理较为困难。为了解决这些问题,需要降低图像的维数。降维是一个从初始高维特征集合中选出低维特征集合,以便根据一定的评估准则最优化缩小特征空间的过程。降维技术在降低数据维数基础上,保留了用于后续分类的有效信息,通常作为机器学习的预处理步骤,在机器学习、文本挖掘、多媒体挖掘、图像处理、异常检测、生物信息学和自然语言处理等许多领域广泛应用。高光谱图像降维处理受到国内外专家学者的高度重视,提出许多降维处理算法,其中具有代表性的方法包括:主成分分析[1]、投影寻踪[2]、自适应波段选择[3]以及聚类方法[4-5]等。目前,很多智能优化算法应用于高光谱图像降维处理,例如粒子群算法[6]、蚁群算法[7]、人工蜂群算法[8]、禁忌搜索算法[9]、烟花算法[10]等,这些智能优化算法具有很好的降维效果,但是也存在降维速度较慢的弊端。连续投影算法(SPA)[11-12]则具有快速降维的特点,是一种使矢量空间共线性最小化的前向变量选择算法,它的优势在于提取全波段的几个特征波段,能够消除原始光谱矩阵中冗余的信息,可用于光谱特征波段的筛选,不仅思想简单,而且参数较少。但是,在传统的SPA算法中,随机选取一个波段作为初始波段,这样选取的波段具有随机性,对后续波段的选择也会有影响,可能带有较多的冗余信息。针对这个问题,我们提出改进的连续投影算法,分别基于峰度值和偏度值进行初始波段选择,保证初始波段的有效性,为选择其他波段打好基础,实现快速又高效的降维,提高后续的分类精度。
1 连续投影算法原理SPA算法属于前向选择算法,首先选出一个初始波段,然后在每一次迭代时加入新的波段,直到达到指定的波段数,这样是为了选出那些具有最小冗余信息的波段,解决共线性问题[13]。SPA作为一种波段选择方法,以其简便、快速的特点得到越来越多的应用,在多种样本波段的提取方面取得了很好的效果。
SPA算法步骤如下[14]:
1)设随机选取的初始迭代向量为Xk(0),并设定需要提取向量的个数为N,即降维后波段数;
2)在第一次迭代(n=1)之前,随机选取光谱矩阵的任意一列j,把校正集光谱矩阵X中的第j列赋值给Xk(0),其中j=1,2,···,(J−1),J,J为所有的波段数。
3)令S是没有被选中的波段集合,那么S可以表示为
| $S = \left\{ {j,1 \leqslant j \leqslant J,j \notin \left\{ {k\left( 0 \right), k(1), \cdots,k\left( {n - 1} \right)} \right\}} \right\}$ |
即去除初始波段后剩下的其他波段的集合。
4)对Xj在子空间中正交于Xk(n-1)的投影进行计算:
| $P{{X}_j} = {{X}_j} - \left( {{X}_j^{\rm{T}} {{X}_{k\left( {n - 1} \right)}}} \right){{X}_{k\left( {n - 1} \right)}}{\left( {{X}_{k\left( {n - 1} \right)}^{\rm{T}} {{X}_{k\left( {n - 1} \right)}}} \right)^{ - 1}}$ | (1) |
式中:
5)式(1)中的k(n)可表示为
| $k\left( n \right) = \arg \left( {\max \left( {\left\| {P{{X}_j}} \right\|,j \in S} \right)} \right)$ |
即步骤3)中求得的N−1个投影值中的最大投影值。
6)将最大投影值作为下次迭代的初始值:
| ${{X}_j} = P{{X}_j},j \in S$ |
7)令n=n+1,如果n<N,则返回到步骤3)循环计算;
8)将降维后得到的所有的波段组合表示为集合W:
| $W = \left\{ {{x_{k\left( n \right)}};n = 0,1, \cdots ,N - 1} \right\}$ |
上述步骤中初始波段的选择即Xk(0)的选择是很重要的一步,因为其可以选择的范围是所有的波段,范围很大,选取的初始波段直接影响后续波段的选择,基于此本文对传统的连续投影算法进行了改进。
2 峰度值与偏度值高光谱图像中的目标相对于背景很小,能够近似为高光谱图像中的异常点,所以要想找到目标特征就相当于寻找目标分布中的偏离,而峰度和偏度能够表示高光谱图像样本的分布形状和特征[15]。其中峰度可以描述分布的集中程度或分布曲线峰部的尖度,偏度则可以表示分布的不对称程度或偏斜程度。下面对峰度与偏度分别定义:
峰度[16]又称峰态系数,表征概率密度分布曲线在平均值处峰值高低的特征数。
随机变量X的4阶标准矩即为峰度:
| ${\beta _2}{\rm{ = }}{\varphi _4}\left( X \right){\rm{ = }}\frac{{{\rm E}\left[ {{{\left( {X - \mu } \right)}^4}} \right]}}{{{{\left\{ {\rm E\left[ {{{\left( {X - \mu } \right)}^2}} \right]} \right\}}^2}}}$ |
式中
| ${\rm E}\left[ {{{\left( {X - \mu } \right)}^4}} \right] = \int_{ - \infty }^{ + \infty } {{{\left( {x - \mu } \right)}^4}} p\left( x \right){\rm d}x$ |
在实际应用中,通常将峰度值做减3处理,所以正态分布的峰度值为零。
偏度[16]是统计数据分布偏斜方向和程度的度量,表征概率分布密度曲线相对于平均值不对称程度的特征数,直观看来就是密度函数曲线尾部的相对长度,表示为
| $\sqrt {{\beta _1}} {\rm{ = }}{\varphi _3}\left( X \right){\rm{ = }}\frac{{{\rm E}\left[ {{{\left( {X - \mu } \right)}^3}} \right]}}{{{{\left\{ {{\rm E}\left[ {{{\left( {X - \mu } \right)}^2}} \right]} \right\}}^{\frac{3}{2}}}}}$ |
所以在高光谱图像处理的过程中,可以利用偏度和峰度系数来衡量包含目标特征信息量的大小以及包含特征在图像中反应差异的大小。因此本文分别选择峰度值和偏度值最大的作为连续投影算法的初始波段。
3 基于峰度值与偏度值的连续投影算法由于连续投影算法具有快速降维的优点,所以将连续投影算法应用于高光谱图像降维,但是将该方法应用于降维的过程中发现,通常只需要将维数降到很低,后期就能实现较好的分类效果,正由于降维后波段数量较少,所以初始波段的选择就显得尤其重要。但是在原始的方法中,对于初始波段的选择通常采用随机选取的方法,这样选出的初始波段可能具有较多的冗余信息,本文将基于此对连续投影算法进行改进。
从SPA算法的原理可以看出,每一个波段的选择都与其前一个波段有关,所以初始波段的选择显得尤其重要。本文将峰度值和偏度值应用于初始波段的选择,提出基于峰度值的连续投影算法(P-SPA)与基于偏度值的连续投影算法(S-SPA),分别选取峰度值和偏度值较大的波段作为初始波段,不仅减小了噪声波段引入的概率,而且实现了对传统连续投影算法的优化处理,在保证降维速度的基础上,提高降维的性能,从而实现高效降维,为之后的分类打下良好基础。
改进算法的流程图如图1所示。

|
Download:
|
| 图 1 改进算法流程 | |
印第安纳数据:该数据来源于AVIRIS传感器,是拍摄于美国西北部印第安纳州的一幅高光谱图像的一部分。图像大小为145×145(空间分辨率200 m),在去除20个低信噪比波段以及水吸收波段后,参与实验的共有200个波段。本文选择其中的3种大豆数据进行仿真实验:每种大豆数据选取500个样本,共1 500个。在每类样本中随机选取250个样本构成具有750个样本的测试样本集;训练样本从剩下的750个样本中选取。仿真实验共分为3组,分别是在每类大豆中随机选取20、30和40个样本作为构成训练样本集。
实验仿真环境:Intel Pentium G2030,3.0 GHz,内存2 GB台式机,Windows7操作系统,利用MATLAB 2015a对算法进行实验。
4.2 实验结果与分析 4.2.1 实验1在训练样本与测试样本个数相同的情况下,将P-SPA、S-SPA与SPA这3种方法进行高光谱图像的降维处理,并分别用相关向量机(RVM)和支持向量机(SVM)对降维后的数据进行分类。由于SPA算法中每个波段的选择都与上一个波段有关,SPA算法的结果随机性较大,在限定降维后波段数的情下,每次分类结果不同,所以本文取10次实验结果的平均值,而P-SPA与S-SPA算法在限定初始波段选择条件后较为稳定,每次实验结果相同,具体实验数据如表1、2所示。
|
|
表 1 RVM实验结果 |
|
|
表 2 SVM实验结果 |
从表1、2的数据可以看出,在训练样本个数相同的情况下,P-SPA和S-SPA的降维波段数都比SPA算法少,应用降维数据分类处理后的总体分类精度(overall accuracy, OA)都有一定的提高。
由表1的数据可以看出,在使用RVM分类且训练样本数为20、30、40时,P-SPA比SPA降维后的波段数少5~25个,总体分类精度提高0.004 0~0.079 0。S-SPA比SPA降维后的波段数少3~47个,总体分类精度分别提高了0.005 3与0.016 3,证明了本文提出的改进算法比原始算法性能好。
由表2的数据可以看出,在使用SVM进行分类且训练样本为20、30、40时,P-SPA比SPA降维后的波段数少4~8个,总体分类精度提高0.001 9~0.009 0。当训练样本个数为30时,SPA与S-SPA的降维后波段数相同,但是总体分类精度提高了0.012 1。训练样本数为20和40时,S-SPA比SPA降维后的波段少3个,总体分类精度分别提高了0.022 9与0.011 1,验证了本文提出改进算法的有效性。
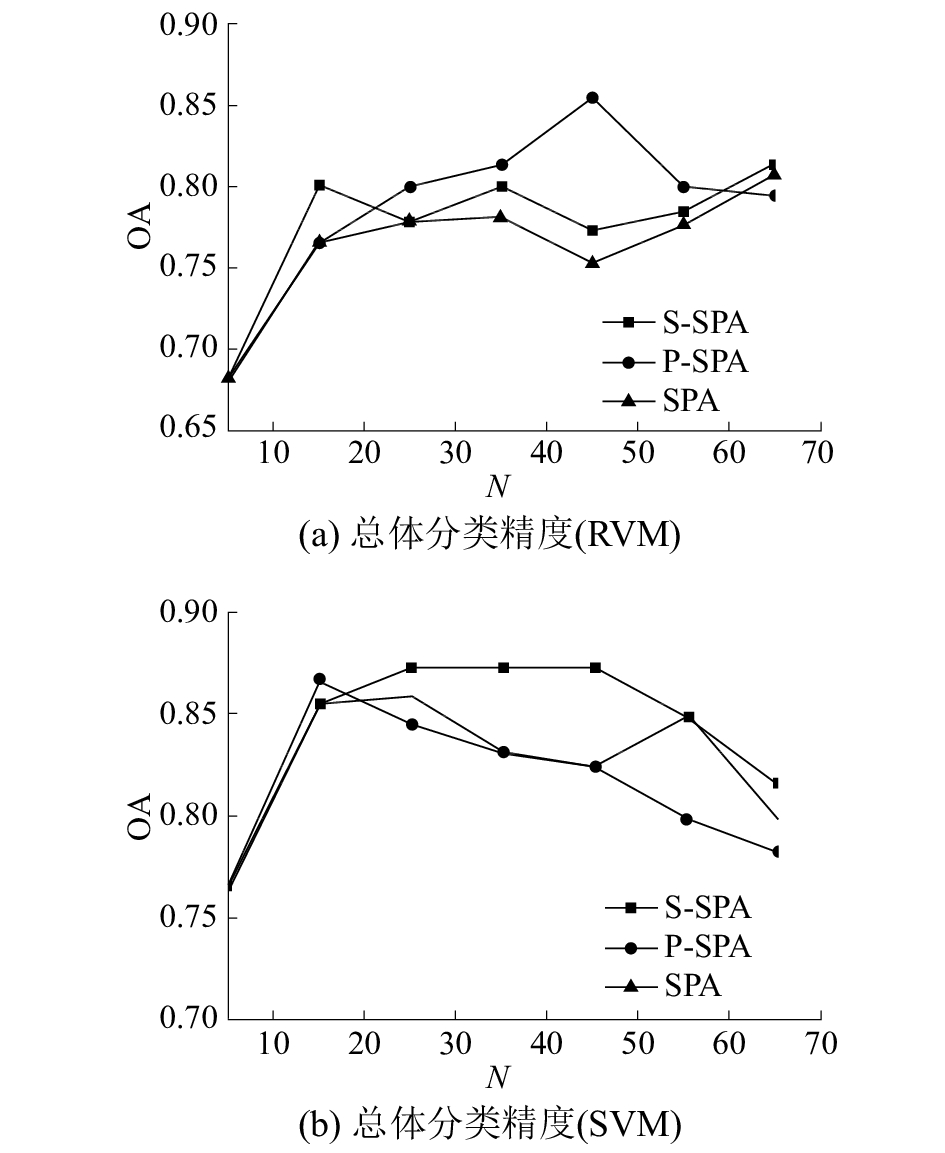
利用SPA、P-SPA与S-SPA方法降维,在训练样本个数均为40的情况下,分别设定降维后的波段数为5、15、25、35、45、55、65,且分别采用RVM与SVM进行分类,实验得出总体分类精度绘制成曲线图如图2所示(其中N表示降维后波段数,OA为总体分类精度)。
|
Download:
|
| 图 2 总体分类精度曲线 | |
由图2(a)可以看出,S-SPA、P-SPA算法在不同的降维波段数下,较于传统的SPA算法,分类性能均有一定的提高。由图2(b)可以看出,S-SPA、P-SPA算法在降维波段数较少的情况下,改进算法较传统算法分类性能提高,但是在波段数较多的情况下,P-SPA会出总体分类精度低于SPA算法的情况,而使用RVM分类时没有出现这种现象,说明了降维方法对于分类的作用与分类器的种类也具有一定的关系,这是由于降维后得到的波段是要输入给分类器处理的,所以降维方法与分类器也需要进行一定的匹配度,才能最大化的发挥降维方法的作用。
4.2.2 实验2为了进一步验证本文改进算法的可靠性,采用蒙特卡罗(MC)算法与S-SPA、P-SPA算法对高光谱图像进行降维,再使用RVM对降维后得到的数据分类,对比实验的结果如表3所示。
|
|
表 3 RVM实验结果 |
由表3可以看出,采用改进算法与MC算法降维后分类,S-SPA与P-SPA算法在保证分类精度的情况下,能够利用更少的波段、以更快的运行速度对高光谱图像数据进行降维及分类处理。采用改进算法与MC算法降维后分类,P-SPA与S-SPA算法在训练样本为20、30个时,均取得了比MC算法更好的效果,实现了高效降维的目的。但是S-SPA算法在训练样本为40时,采用RVM分类的总体分类精度偏低,较MC算法的精度值降低了0.053 7,但是降维波段数减少了100个,时间节省了83.06%。
5 结论本文对传统的SPA算法进行改进,主要完成以下几方面的工作:
1)针对SPA算法中随机选取初始波段的缺点,分别以峰度值和偏度值的大小作为选择初始波段的标准,提出了P-SPA与S-SPA两种降维方法。
2)在AVIRIS数据集上将SPA、P-SPA与S-SPA算法分别应用于相似地物数据降维,将降维后的数据分别采用RVM和SVM分类器进行分类。对比实验结果表明本文提出的算法较原始的连续投影算法性能具有一定的提高。
3)为了进一步验证改进算法的有效性,将P-SPA、S-SPA与MC算法进行对比,通过RVM的分类结果表明本文提出的S-SPA、P-SPA算法在保证分类精度的前提下,具有更快的速度,达到了高效的目的。
4)对于S-SPA算法在训练样本为40时,使用RVM分类精度较低的问题,说明S-SPA算法还具有一定的局限性,在今后的工作中还会对此进行进一步的研究。
| [1] |
LICCIARDI G, MARPU P R, CHANUSSOT J, et al. Linear versus nonlinear PCA for the classification of hyperspectral data based on the extended morphological profiles[J]. IEEE geoscience and remote sensing letters, 2012, 9(3): 447-451. DOI:10.1109/LGRS.2011.2172185 ( 0) 0)
|
| [2] |
王秀朋. 基于投影寻踪的高光谱图像降维算法研究[D]. 西安: 西北工业大学, 2006: 38-43.
( 0) 0)
|
| [3] |
刘春红, 赵春晖, 张凌雁. 一种新的高光谱遥感图像降维方法[J]. 中国图像图形学报, 2005, 10(2): 218-222. ( 0) 0)
|
| [4] |
秦方普, 张爱武, 王书民, 等. 基于谱聚类与类间可分性因子的高光谱波段选择[J]. 光谱学与光谱分析, 2015, 35(5): 1357-1364. DOI:10.3964/j.issn.1000-0593(2015)05-1357-08 ( 0) 0)
|
| [5] |
MARTÍNEZ-USÓMARTINEZ-USO A, PLA F, SOTOCA J M, et al. Clustering-based hyperspectral band selection using information measures[J]. IEEE transactions on geoscience and remote sensing, 2007, 45(12): 4158-4171. DOI:10.1109/TGRS.2007.904951 ( 0) 0)
|
| [6] |
SU Hongjun, DU Qian, CHEN Genshe, et al. Optimized hyperspectral band selection using particle swarm optimization[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2014, 7(6): 2659-2670. DOI:10.1109/JSTARS.2014.2312539 ( 0) 0)
|
| [7] |
TIWARI R, HUSAIN M, GUPTA S, et al. Improving ant colony optimization algorithm for data clustering[C]//Proceedings of the International Conference and Workshop on Emerging Trends in Technology. New York, USA, 2010: 529-534.
( 0) 0)
|
| [8] |
王立国, 赵亮, 刘丹凤. 基于人工蜂群算法高光谱图像波段选择[J]. 哈尔滨工业大学学报, 2015, 47(11): 82-88. DOI:10.11918/j.issn.0367-6234.2015.11.014 ( 0) 0)
|
| [9] |
CUI Ying, WANG Jiaqi, LIU Shubin, et al. Hyperspectral image feature reduction based on tabu search algorithm[J]. Journal of information hiding and multimedia signal processing, 2015, 6(1): 154-162. ( 0) 0)
|
| [10] |
崔颖, 宋国娇, 陈立伟, 等. 基于烟花算法降维的高光谱图像分类[J]. 华南理工大学学报: 自然科学版, 2017, 45(3): 20-28. ( 0) 0)
|
| [11] |
ARAÚJO M C U, SALDANHA T C B, GALVAO R K H, et al. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis[J]. Chemometrics and intelligent laboratory systems, 2001, 57(2): 65-73. DOI:10.1016/S0169-7439(01)00119-8 ( 0) 0)
|
| [12] |
FILHO H A D, GALVÃO R K H, ARAÚJO M C U, et al. A strategy for selecting calibration samples for multivariate modelling[J]. Chemometrics and intelligent laboratory systems, 2004, 72(1): 83-91. DOI:10.1016/j.chemolab.2004.02.008 ( 0) 0)
|
| [13] |
郝勇, 孙旭东, 王豪. 基于改进连续投影算法的光谱定量模型优化[J]. 江苏大学学报: 自然科学版, 2013, 34(1): 49-53. ( 0) 0)
|
| [14] |
陈斌, 孟祥龙, 王豪. 连续投影算法在近红外光谱校正模型优化中的应用[J]. 分析测试学报, 2007, 26(1): 66-69. DOI:10.3969/j.issn.1004-4957.2007.01.016 ( 0) 0)
|
| [15] |
寻丽娜, 方勇华. 基于投影寻踪的高光谱图像目标检测算法[J]. 光子学报, 2006, 35(10): 1584-1588. ( 0) 0)
|
| [16] |
田禹. 基于偏度和峰度的正态性检验[D]. 上海: 上海交通大学, 2012.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


