2. 哈尔滨工业大学 空间控制与惯性技术研究中心, 黑龙江 哈尔滨 150001
2. Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China
陆地自主车的基础模型就是一种室内作业机器人,由于其在军事领域的广泛应用正受到学者们的普遍关注[1]。以陆地自主车为载体,在其基础上匹配各种先进监控技术并应用于复杂环境是目前大多数领域应用的模式,如何对其实施简单有效且方便执行的控制策略是研究和推广的关键[2]。陆地自主车典型的数学模型就是一类参数不确定广义分段仿射系统,按照不同运行速度将整个大系统区分为若干个带仿射项的子系统,并在每一个子系统之间反复切换。目前,广义系统鲁棒控制问题已成为广大学者研究的热点之一,在传统控制器设计问题上考虑非脆弱性能引入的相关研究也取得了一些进展[3-5],所涉及的控制系统大多体现为离散时间系统,控制策略的设计方法大多采用分段Lyapunov函数法,在此基础上结合相应线性矩阵不等式的处理方法[6-9]。然而,在连续时间系统领域考虑时滞环节与非脆弱环节并存的鲁棒控制设计方法却未见报道。
本文主要研究内容围绕分段Lyapunov函数、投影定理以及几个基本引理展开,在先前研究的基础上引入非脆弱H-infinite保性能控制设计方法,对连续时间陆地自主车系统设计一种同时满足鲁棒H-infinite和二次型性能指标的控制策略。最终,通过MATLAB仿真给出所提方法的有效性。
1 数学建模陆地自主车的简化数学模型如图 1所示,xzy用来表示地理直角坐标系,xBoyB用来表示车体体位直角坐标系,ψ则用来表示车体行进的实时方向与实地物理坐标系x轴方向的夹角,一般也称方向角[10]。

|
Download:
|
| 图 1 系统数学模型 | |
在数学建模过程之前,假定车体前进方向就是本身的运动方向,且用恒量u0表示,将自主车所受z方向的力矩T作为系统输入,一段时间以后,对整个系统实施鲁棒控制的最终目的在于保持恒速u0前进的前提下,使得:y=0, ψ=0,此时可以列出如下方程:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \psi }\\ {\dot \omega }\\ {\dot y}\\ {\dot \varpi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ 0&{ - \frac{k}{I}}&0&0\\ 0&0&0&0\\ 0&k&0&I \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \psi \\ \omega \\ y\\ \varpi \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{u_0}\sin \psi }\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{I}}\\ 0\\ { - 1} \end{array}} \right]T} \end{array} $ | (1) |
其中各物理量的具体含义如表 1所示。
|
|
表 1 各物理量的具体含义 |
在此假设通过测量可以得到车体行进方向角,通过观察式(1)可知,有非线性项sin ψ出现在该动态方程中,通过假设并定义方向角的取值波动在
|
|
表 2 不同区域取值范围 |
利用泰勒公式将sinψ展开,忽略最高次项并整理为线性形式得
| $ \sin \psi \approx \sin {\psi _i} + \cos {\psi _i}\left( {\psi - {\psi _i}} \right),i = 1,2, \cdots ,5 $ |
则式(1)可以进一步改写为式(2):
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \psi }\\ {\dot \omega }\\ {\dot y}\\ {\dot \varpi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ 0&{ - \frac{k}{I}}&0&0\\ 0&0&0&0\\ 0&k&0&I \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \psi \\ \omega \\ y\\ \varpi \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{u_0}\left( {\sin {\psi _i} - {\psi _i}\cos {\psi _i}} \right)}\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{I}}\\ 0\\ { - 1} \end{array}} \right]T} \end{array} $ | (2) |
式中:ψ∈Xi, i=1, 2, …, 5,对应5个不同的工作点,取值分别为-2π/5、-2π/15、0、2π/15、2π/5。
取I=1 kgm2, k=0.01, u0=1 m/s, u=T为系统输入,系统的状态向量分别为角加速度、车体方向角、y方向的位移以及方向角速度,各状态向量之间的关系如式(3)所示:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {x_4}\\ {{\dot x}_2} = - \frac{k}{\mathit{\boldsymbol{I}}}{x_2} + \frac{1}{\mathit{\boldsymbol{I}}}u\\ {{\dot x}_3} = {u_0}\sin {x_1} \end{array} \right. $ | (3) |
通过建立系统各变量之间的数学关系,同时考虑系统时滞τ(t)带来的影响,可以得到在广义系统表述形式下的陆地自主车数学模型,如式(4)所示:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{E\dot x}}\left( t \right) = \left( {{\mathit{\boldsymbol{A}}_i} + \Delta {\mathit{\boldsymbol{A}}_i}} \right)\mathit{\boldsymbol{x}}\left( t \right) + \left( {{\mathit{\boldsymbol{A}}_{di}} + \Delta {\mathit{\boldsymbol{A}}_{di}}} \right)\mathit{\boldsymbol{x}}\left( {t - \tau \left( t \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{u}}\left( t \right) + \mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{b}}_i} + \Delta {\mathit{\boldsymbol{b}}_i}} \right),\\ \mathit{\boldsymbol{y}}\left( t \right) = \varphi \left( t \right),t \in \left[ { - h,0} \right] \end{array} \right. $ | (4) |
式中:x(t)∈Rnx,为系统状态变量;u(t)∈Rnu,为控制输入向量;y(t)∈Rny,为系统输出向量;φ(t)是初始条件,τ(t)系统的变时滞,并且0≤τ(t)≤h,
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{i}}}}&{\Delta {\mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{di}}}}}&{\mathit{\boldsymbol{E}}\Delta {\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{i}}}} \end{array}} \right] = }\\ {{\mathit{\boldsymbol{W}}_{{\mathit{\boldsymbol{i}}_1}}}{\Delta _i}\left( t \right)\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{E}}_{{i_1}}}}&{{\mathit{\boldsymbol{E}}_{{i_2}}}}&{{\mathit{\boldsymbol{E}}_{{i_3}}}} \end{array}} \right],i \in I} \end{array} $ | (5) |
式中:Wi1、Ei1、Ei2和Ei3是预先指定的定常实数矩阵,Δi(t):Z+→Rs1×s2是一个未知的实值时变矩阵函数,并且包含Lebesgue可测量元素,具体如式(6)。
| $ {\Delta _i}^{\rm{T}}\left( t \right){\Delta _i}\left( t \right) \le {I_{{s_2}}} $ | (6) |
如果式(5)和式(6)同时成立,则称系统具有容许的参数不确定性。
2 预备知识 2.1 状态空间区域划分在仿射子系统中,线性化处理区间可描述为多面体区域的椭圆集合,其中Fi=2Ci/(βi-αi),fi=-(βi+αi)/(βi-αi);εi={x|‖Fix+fi‖≤1},其中,i∈I。
对于每个椭圆区域,可以得到
| $ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( t \right)}\\ 1 \end{array}} \right]^{\rm{T}}}\left[ {{\mathit{\boldsymbol{F}}_i}^{\rm{T}}{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}_i}^{\rm{T}}{\mathit{\boldsymbol{f}}_i}{\mathit{\boldsymbol{f}}_i}^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( t \right)}\\ 1 \end{array}} \right] \le 0,i \in I $ | (7) |
因此,状态空间可以分为两大类区域I=I0∪I1,I0代表包含原点的fiTfi≤x(t)THx(t),I1则代表其余的索引集合区域。
2.2 基本引理定义1[11] 考虑参数不确定体现为范数有界形式的离散广义分段仿射系统(1),其中u(t)=0:
1) 如果存在z∈C使得det(zE-Ai)≠0,则称广义系统(1)是正则的,i∈I。
2) 如果deg(det(zE-Ai))=rank(E), i∈I,则称系统(1)是因果广义系统。
3) 用λ(E, Ai)表示离散广义系统(1)的所有特征根,如果λ(E, Ai)⊂Dint(0, 1),则称式(1)是稳定的广义系统。
4) 如果称广义系统(1)是容许的,则系统(1)必定正则、因果,而且是稳定的。
5) 用ν1表示矩阵束(E, Ai)的一阶向量,且非零向量ν1满足Eν1=0,对于满足Eνk=Aivk-1的非零特征向量νk(k≥2),则称为矩阵束(E, Ai)的k阶特征向量。
定义2 本文所设计鲁棒H-infinite非脆弱状态反馈控制器:
| $ \mathit{\boldsymbol{u}}\left( \mathit{\boldsymbol{t}} \right) = {{\mathit{\boldsymbol{\bar K}}}_i}\left( t \right)x\left( t \right) = \left( {{\mathit{\boldsymbol{K}}_i} + \Delta {\mathit{\boldsymbol{K}}_i}\left( t \right)} \right)x\left( t \right),i \in I $ |
式中:Ki∈Rnu×nx是控制器的增益矩阵;ΔKi(t)是控制器中的不确定项,ΔKi(t)=MKFK(t)NK;MK、NK是已知的适当维数线性矩阵,并且FK(t)TFK(t)≤I。
引理1 对于适当维数实矩阵M=MT、S、N和Δ(t),若满足ΔT(t)Δ(t)≤I,则当且仅当存在某个标量ε>0时:M+SΔ(t)N+NTΔT(t)ST < 0等价于M+εSST+ε-1NTN < 0。
引理2 定义θ的矩阵函数R1(θ)、R2(θ)和R3(θ),如下线性矩阵不等式LMI:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1}\left( \theta \right){\mathit{\boldsymbol{R}}_2}\left( \theta \right)}\\ {\mathit{\boldsymbol{R}}_2^{\rm{T}}\left( \theta \right){\mathit{\boldsymbol{R}}_3}\left( \theta \right)} \end{array}} \right] < 0 $ |
在不同的情况下等价于以下2个不等式:
| $ {\mathit{\boldsymbol{R}}_1}\left( \theta \right) < 0,{\mathit{\boldsymbol{R}}_3}\left( \theta \right) - \mathit{\boldsymbol{R}}_2^{\rm{T}}\left( \theta \right)\mathit{\boldsymbol{R}}_1^{ - {\rm{1}}}\left( \theta \right){\mathit{\boldsymbol{R}}_2}\left( \theta \right) < 0, $ |
| $ {\mathit{\boldsymbol{R}}_3}\left( \theta \right) < 0,{\mathit{\boldsymbol{R}}_1}\left( \theta \right) - {\mathit{\boldsymbol{R}}_2}\left( \theta \right)\mathit{\boldsymbol{R}}_3^{ - {\rm{1}}}\left( \theta \right)\mathit{\boldsymbol{R}}_2^{\rm{T}}\left( \theta \right) < 0。$ |
对于分段仿射系统(4),考虑性能指标:
| $ J = \int_0^\infty {\left( {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{Qx}}\left( t \right) + \mathit{\boldsymbol{u}}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{Ru}}\left( t \right)} \right){\rm{d}}t} $ | (8) |
本文所考虑弹性状态反馈控制器由定义2给出,由此弹性控制器和连续广义分段仿射系统(4)构成的闭环系统可以描述如下:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{E\dot x}}\left( t \right) = \left( {{\mathit{\boldsymbol{A}}_i}\left( t \right) + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{i}}}{{\bar K}_i}\left( t \right)} \right)x\left( t \right) + \\ {\mathit{\boldsymbol{A}}_{di}}\left( t \right)x\left( {t - \tau \left( t \right)} \right) + {\mathit{\boldsymbol{D}}_i}\left( t \right)w\left( k \right) + \mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{b}}_i} + \Delta {\mathit{\boldsymbol{b}}_i}} \right)\\ x\left( t \right) = \varphi \left( t \right),t \in \left[ { - h,0} \right]\\ z\left( t \right) = {\mathit{\boldsymbol{L}}_i}\left( t \right)x\left( t \right) \end{array} \right. $ | (9) |
式中:Ai(t)=Ai+ΔAi, Adi(t)=Adi+ΔAdi, Ki(t)=Ki+ΔKi(t)。
定理 对于所提弹性控制器,如果存在对称正定矩阵0 < Pi=PiT∈Rnx×nx,i∈I,0 < ϑ=ϑT∈Rnx×nx,以及实数εij, i∈I, (i, j)∈Ω,使式(10)~ (12)成立:
| $ {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} \ge 0 $ | (10) |
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\gamma ^{ - 2}}I}&0&{{\mathit{\boldsymbol{L}}^i}}&{{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{A}}_{di}}\left( t \right)}&{{\mathit{\boldsymbol{H}}_1}^{\rm{T}}}\\ * &\Lambda &0&0&0\\ *&* &{\mathit{\boldsymbol{T}} + \mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{ \boldsymbol{\varPi} }}}&0&0\\ *&*&* &{\left( {\eta - 1} \right)\vartheta }&0\\ *&*&*&* &{ - {\varepsilon _{ij}}I} \end{array}} \right] < 0}\\ {i \in {I_0},\left( {i,j} \right) \in \Omega } \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\gamma ^{ - 2}}I}&0&{{\mathit{\boldsymbol{L}}_i}}&0&{{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{A}}_{di}}\left( t \right)}&{{\mathit{\boldsymbol{H}}_1}^{\rm{T}}}\\ * &\Lambda &0&0&0&0\\ *&* &{\mathit{\boldsymbol{T}} + \mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{ \boldsymbol{\varPi} }}}&0&0&0\\ *&*&* &{{{\rm{ \mathsf{ π} }}^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}I} \right){\rm{ \mathsf{ π} }}}&0&0\\ *&*&*&* &{\left( {\eta - 1} \right)\vartheta }&0\\ *&*&*&*&* &{ - {\varepsilon _{ij}}I} \end{array}} \right] < 0}\\ {i \in {I_1},\left( {i,j} \right) \in \Omega } \end{array} $ | (12) |
式中:Τ=(Ai(t)+biKi(t))TPi+Pi(Ai(t)+BKi(t)),π=E(bi+Δbi),则由连续时间时滞广义分段仿射系统(4)和所提非脆弱状态反馈控制器构成的闭环系统(9)既是容许的又满足一定的鲁棒性能指标,且此闭环系统存在一个性能上界:
| $ J \le {J^ * } = {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\left( 0 \right){\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E\varphi }}\left( 0 \right) + \int_{ - d}^0 {{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\left( s \right){\mathit{\boldsymbol{\vartheta}}} \left( s \right){\rm{d}}s} $ |
证明 在这里,采用的李雅普诺夫函数是定义在连续时间范畴内的,具体广义分段仿射李雅普诺夫函数形式表示如下:
| $ V\left( {x,t} \right) = {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right){\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{Ex}}\left( t \right) + \int_{t - \tau \left( t \right)}^t {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( s \right){\mathit{\boldsymbol{\vartheta}}} \mathit{\boldsymbol{x}}\left( s \right){\rm{d}}s} ,i \in I $ |
设计控制策略的目的在于另闭环系统式(9)是容许的,根据连续时滞广义分段仿射李雅普诺夫函数的形式,只需要保证不等式(13)成立。在这一过程中,对李雅普诺夫函数式两边沿闭环系统式(9)同时进行求导,进一步得到式(13):
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}}\left( {x,t} \right) = {\mathit{\boldsymbol{x}}^{\rm{T}}}{{\left( t \right)}_{11}}x\left( t \right) + 2{{\rm{ \mathsf{ π} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}x\left( t \right) + }\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right){\mathit{\boldsymbol{P}}_i}\pi + {\pi ^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}I} \right)\pi < 0} \end{array} $ | (13) |
进一步,为保证闭环系统式(9)即是容许的又满足鲁棒性能指标γ,另不等式(14)成立:
| $ \mathit{\boldsymbol{\dot V}}\left( {x,t} \right) + {\gamma ^{ - 2}}{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right) - {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right) < 0 $ | (14) |
根据闭环系统式(9)中z(t)=Li(t)x(t),则不等式(14)进一步可以写成如下形式:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}}\left( {x,t} \right) + {\gamma ^{ - 2}}{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right) - {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right) = }\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}{{\left( t \right)}_{11}}x\left( t \right) + 2{{\rm{ \mathsf{ π} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}x\left( t \right) + {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right){\mathit{\boldsymbol{P}}_i}{\rm{ \mathsf{ π} }} - {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right) + }\\ {{{\rm{ \mathsf{ π} }}^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}I} \right){\rm{ \mathsf{ π} }} + {\gamma ^{ - 2}}{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right) + {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{D}}_i^{\rm{T}}{\mathit{\boldsymbol{D}}_i}\mathit{\boldsymbol{w}}\left( t \right) < 0} \end{array} $ |
其中:
| $ \begin{array}{*{20}{c}} {_{11} = {{\left( {{\mathit{\boldsymbol{A}}_i}\left( t \right) + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar K}}}_i}\left( t \right)} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i} + {\mathit{\boldsymbol{P}}_i}\left( {{\mathit{\boldsymbol{A}}_i}\left( t \right) + {\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{i}}}{{\mathit{\boldsymbol{\bar K}}}_i}\left( t \right)} \right) + {\mathit{\boldsymbol{\vartheta}}} + }\\ {\frac{1}{{1 - \eta }}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{A}}_{di}}\left( t \right){{\mathit{\boldsymbol{\vartheta}}} ^{ - 1}}{\mathit{\boldsymbol{A}}_{di}}{{\left( {^t} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i} + \varepsilon _{ij}^{ - 1}\mathit{\boldsymbol{H}}_1^{\rm{T}}{\mathit{\boldsymbol{H}}_1},{\rm{ \mathsf{ π} }} = \mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{i}}} + \Delta {\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{i}}}} \right)} \end{array} $ |
不等式(14)可进一步改写为如下形式,其中(i, j)∈Ω:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}}\left( {x,t} \right) + {\gamma ^{ - 2}}{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right) - {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right) = }\\ {{{\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{w}}\left( t \right)}\\ {\mathit{\boldsymbol{x}}\left( t \right)}\\ 1 \end{array}} \right]}^{\rm{T}}}\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_i}^{\rm{T}}\left( t \right)}&0&0\\ 0&{_{11}}&{{\mathit{\boldsymbol{P}}_i}{\rm{ \mathsf{ π} }}}\\ 0&{{{\rm{ \mathsf{ π} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}}&{{{\rm{ \mathsf{ π} }}^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}I} \right){\rm{ \mathsf{ π} }}} \end{array}} \right] + \\ {\gamma ^{ - 2}}\left[ {\begin{array}{*{20}{c}} 0\\ {\mathit{\boldsymbol{L}}_i^{\rm{T}}}\\ 0 \end{array}} \right]\left( * \right) + \left[ {\begin{array}{*{20}{c}} { - I}&0&0\\ * &{ - {E^{\rm{T}}}{P_i}E}&0\\ *&* &0 \end{array}} \right] \end{array} \right\}\left[ {\begin{array}{*{20}{c}} {w\left( t \right)}\\ {x\left( t \right)}\\ 1 \end{array}} \right] < 0} \end{array} $ |
可以得到:
| $ {\mathit{\boldsymbol{A}}_i}{\left( t \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{A}}_i}\left( t \right) - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} < 0 $ | (15) |
这里,进一步假定矩阵束(E, Ai(t))为非因果的。用一阶特征向量ν1和它的Hermitian矩阵ν1*分别左乘和右乘式(15)。用文献[10]的方法,证明因果性的同时也证明了矩阵束(E, Ai(t))的正则性。
进一步将式(14)等同为如下形式:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\gamma ^{ - 2}}I}&0&{{\mathit{\boldsymbol{L}}_i}}&0\\ * &\Lambda &0&0\\ *&* &{_{11} - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}}}&{{\mathit{\boldsymbol{P}}_i}{\rm{ \mathsf{ π} }}}\\ *&*&* &{{{\rm{ \mathsf{ π} }}^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}I} \right){\rm{ \mathsf{ π} }}} \end{array}} \right] < }\\ {0,\left( {i,j} \right) \in \mathit{\Omega }} \end{array} $ |
其中:Λ=DiT(t)-I。
考虑系统性能指标(8),为了使闭环系统(9)同时满足鲁棒性能指标和二次型性能指标,只需要令如下不等式成立即可:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}}\left( {x,t} \right) + {\gamma ^{ - 2}}{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right) - {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right) + }\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{Qx}}\left( t \right) + \mathit{\boldsymbol{u}}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{Ru}}\left( t \right) \le 0} \end{array} $ |
其中:u(t)=(Ki+ΔKi(t))x(t),进而得到如下不等式:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\gamma ^{ - 2}}\mathit{\boldsymbol{I}}}&0&{{\mathit{\boldsymbol{L}}^i}}&0\\ * &\Lambda &0&0\\ *&* &\mathit{\Omega }&{{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{R}}}\\ *&*&* &{{\mathit{\boldsymbol{R}}^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{R}}} \end{array}} \right] < 0,}\\ {\left( {i,j} \right) \in \mathit{\Omega }} \end{array} $ |
式中:Ω=Ψ11-ETPiE+Q+Ki(t)TRKi(t)。
应用引理2,可以得到如下不等式:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\gamma ^{ - 2}}\mathit{\boldsymbol{I}}}&0&{{\mathit{\boldsymbol{L}}^i}}&0&{\mathit{\boldsymbol{H}}_1^{\rm{T}}}\\ * &\Lambda &0&0&0\\ *&* &{\mathit{\boldsymbol{T}} + \mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}}}&{{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{R}}}&0\\ *&*&* &{{\mathit{\boldsymbol{R}}^{\rm{T}}}\left( { - {\varepsilon _{ij}}^{ - 1}\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{R}}}&0\\ *&*&*&* &{ - {\varepsilon _{ij}}\mathit{\boldsymbol{I}}} \end{array}} \right] < 0,}\\ {\left( {i,j} \right) \in \mathit{\Omega }} \end{array} $ |
其中:
| $ T = {\left( {{\mathit{\boldsymbol{A}}_i}\left( t \right) + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{i}}}{{\mathit{\boldsymbol{\bar K}}}_i}\left( t \right)} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_i} + {\mathit{\boldsymbol{P}}_i}\left( {{\mathit{\boldsymbol{A}}_i}\left( t \right) + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{i}}}{{\mathit{\boldsymbol{\bar K}}}_i}\left( t \right)} \right), $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = {{\mathit{\boldsymbol{\bar K}}}_i}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{R}}{{\mathit{\boldsymbol{\bar K}}}_i}\left( t \right) + \vartheta + \frac{1}{{1 - \eta }}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{A}}_{di}}\left( t \right){\vartheta ^{ - 1}}{\mathit{\boldsymbol{A}}_{di}}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{P}} $ |
再次应用引理2,可以得到如下不等式:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\gamma ^{ - 2}}I}&0&{{\mathit{\boldsymbol{L}}^i}}&0&{{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{A}}_{di}}\left( t \right)}&{\mathit{\boldsymbol{H}}_1^{\rm{T}}}\\ * &\Lambda &0&0&0&0\\ *&* &{\mathit{\boldsymbol{T}} + \mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{ \boldsymbol{\varPi} }}}&{{\mathit{\boldsymbol{P}}_i}{\rm{ \mathsf{ π} }}}&0&0\\ *&*&* &{{{\rm{ \mathsf{ π} }}^{\rm{T}}}\left( { - \varepsilon _{ij}^{ - 1}\mathit{\boldsymbol{I}}} \right){\rm{ \mathsf{ π} }}}&0&0\\ *&*&*&* &{\left( {\eta - 1} \right)\vartheta }&0\\ *&*&*&*&* &{ - {\varepsilon _{ij}}\mathit{\boldsymbol{I}}} \end{array}} \right] < 0,}\\ {\left( {i,j} \right) \in \mathit{\Omega }} \end{array} $ |
式中Π=Ki(t)TRKi(t)+ϑ-ETPiE。
由于
| $ \begin{array}{*{20}{c}} {J = \int_0^\infty {\left( {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{Q}}x\left( t \right) + \mathit{\boldsymbol{u}}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{Ru}}\left( t \right)} \right){\rm{d}}t} \le \mathit{\boldsymbol{V}}\left( {x\left( 0 \right)} \right) = }\\ {{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\left( 0 \right){\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E\varphi }}\left( 0 \right) + \int_{ - d}^0 {{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\left( s \right){\mathit{\boldsymbol{\vartheta}}} \left( s \right){\rm{d}}s} = {J^ * }} \end{array} $ |
证毕。
本文定理给出了参数不确定时滞广义分段仿射系统式(9)在连续时间范畴内控制器存在的充分条件,将问题转换为MATLAB中LMI工具箱的求解,寻求同时满足鲁棒性能指标和二次型性能指标的控制器增益。
4 分析仿真首先,应用本文所提定理设计陆地自主车分段仿射系统的非脆弱闭环控制器,证实本文所提控制方法的有效性,接下来通过对比参考文献中所提闭环系统控制方法,证实本文所提控制方法的优越性,给出此类离散广义分段仿射系统鲁棒H-infinite静态输出反馈控制器求取的正确途径。
给定闭环控制系统的扰动输入w(k)=10e-t,利用MATLAB7.0线性矩阵不等式工具箱中的mincx求解器,得到欲寻求的输出反馈控制器增益矩阵:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_1} = 9.278\;1,{\mathit{\boldsymbol{K}}_2} = 6.567\;8,{\mathit{\boldsymbol{K}}_3} = 7.002\;1,}\\ {{\mathit{\boldsymbol{K}}_4} = 0.213\;6,{\mathit{\boldsymbol{K}}_5} = 17.731\;1} \end{array} $ |
最终,保证此类离散广义分段仿射系统不仅是渐近稳定的,而且同时满足一定的鲁棒H-infinite性能指标和二次型性能指标:γ=21.425 4。
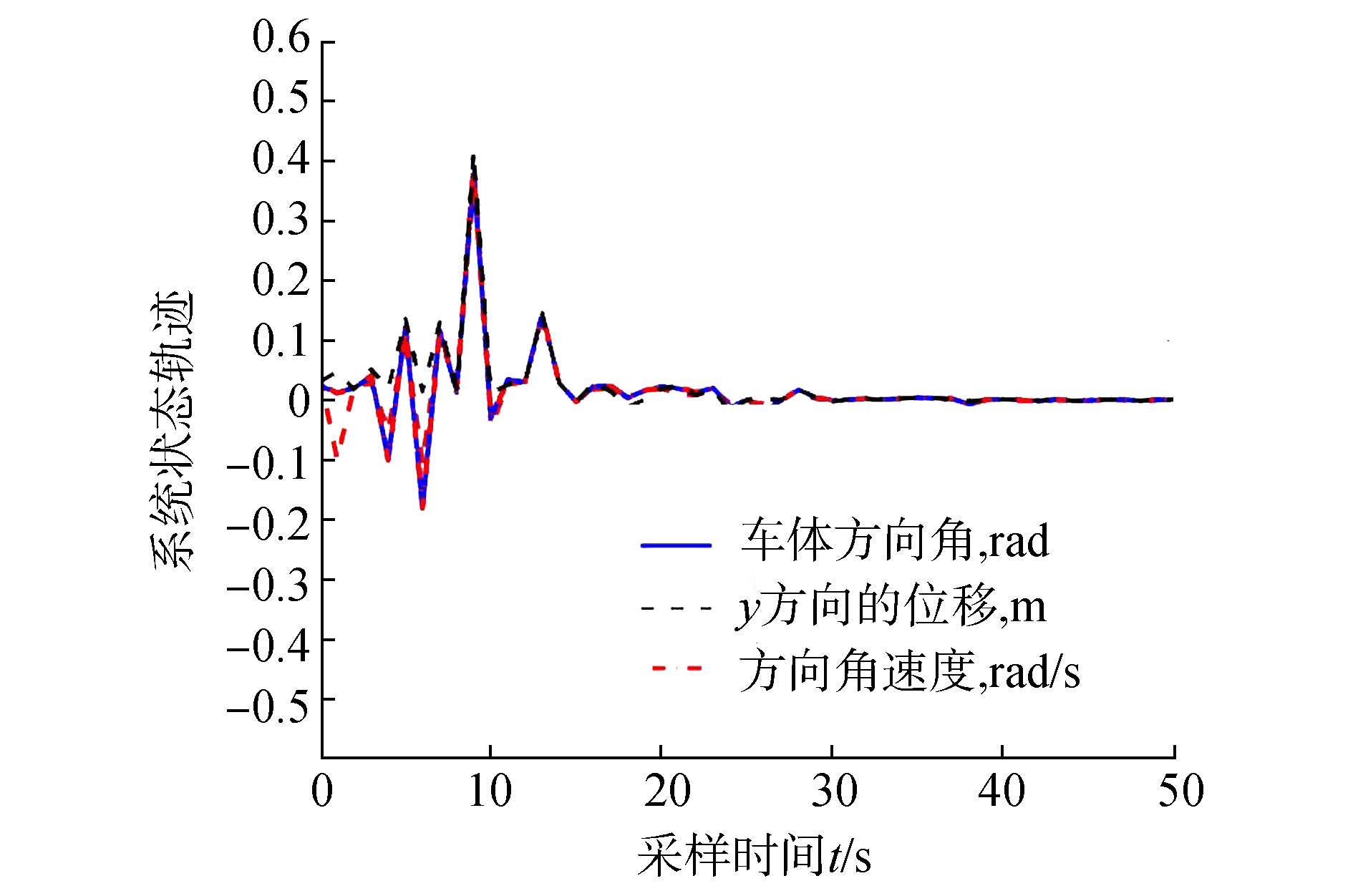
数值仿真所给闭环控制系统状态响应曲线如图 2所示。
|
Download:
|
| 图 2 闭环操作系统响应曲线 | |
接下来,将本文所提控制器设计方法和文献[12]中所提算法进行对比,定义该陆地自主车中广义矩阵E=I,此时系统降为正常系统,如式(16)所示。
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\dot \psi }\\ {\dot \omega }\\ {\dot y} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&{ - \frac{k}{\mathit{\boldsymbol{I}}}}&0\\ {{u_0}\cos {\psi _i}}&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \psi \\ \omega \\ y \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{\mathit{\boldsymbol{I}}}}\\ 0 \end{array}} \right]T + }\\ {\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{u_0}\left( {\sin {\psi _i} - {\psi _i}\cos {\psi _i}} \right)} \end{array}} \right]} \end{array} $ | (16) |
考虑系统存在扰动输入w(k)=10e-t的情况,根据表 3所示将车体行进速度取为不同阶段的值,利用本文定理和文献[12]中的结果分别计算获得的最小鲁棒H-infinite性能指标γ。通过观察表 3中针对不同速度下的性能指标,进一步证实本文所提控制策略具有一定的卓越性。
|
|
表 3 几种行进速度下的H-infinite性能指标γ |
值得注意的是,当车体速度u0≥2 m/s时,文献[12]中所提算法将无法求得最小鲁棒H-infinite性能指标γ,即当扰动输入存在时,采用本文所提定理具有更好的鲁棒性,可以针对更多情况下的车体行进速度找到非脆弱状态输出反馈控制器使得闭环系统同时具有鲁棒H-infinite性能指标γ和二次型性能指标。
接下来,为了说明系统二次D-稳定性和闭环系统鲁棒H-infinite性能的关系,规定车体行进方向角的取值范围为
|
|
表 4 不同区域取值范围 |
表中ψ∈Χi, i=1, 2, 3对应3个不同的工作点,取值分别为:-2π/15,0,2π/15。
同样,根据本文定理以及文献[12]中所提算法对式(2)在各个线性工作点附近做线性化处理,基于此种方法得到非脆弱反馈控制器,最终在区域Χ2内使得闭环系统稳定于平衡点(0, 0, 0)处,从而达到控制目的。
考虑系统存在扰动输入w(k)=10e-t的情况,通过本文定理构造闭环控制器,再利用MATLAB7.0线性矩阵不等式工具箱中的mincx求解器进行演算,求得欲寻求的输出反馈非脆弱控制器增益矩阵:
| $ {\mathit{\boldsymbol{K}}_1} = 14.964\;5,{\mathit{\boldsymbol{K}}_2} = 23.453\;5,{\mathit{\boldsymbol{K}}_3} = 5.547\;8 $ |
此时,针对陆地自主车运行时的各物理量取为:I=1.5kgm2, k=0.05, u=T为系统输入。利用本文定理和文献[12]中的结果分别计算获得的最小鲁棒H-infinite性能指标γ,使得由非脆弱状态输出反馈控制器构成的闭环系统同时具有鲁棒H-infinite性能指标γ和二次型性能指标,2个闭环系统状态响应曲线由图 3、4给出。

|
Download:
|
| 图 3 闭环操作系统响应曲线(根据本文所提定理所得) | |

|
Download:
|
| 图 4 闭环操作系统响应曲线(根据参考文献所得) | |
对仿真过程所得到的数据进行分析比较可以看出,基于本文所提出方法设计的非脆弱保性能控制器使得闭环系统(9)渐近稳定,H-infinite扰动抑制度γ=86.900 2,且存在一个性能上界J < 6.754 7,满足欲达到的设控制目的。另一方面,根据文献[12]中所提算法设计的控制器同样使得闭环系统(9)渐近稳定,同时得到闭环系统的H-infinite干扰抑制度γ=17.095 4。
将图 3、4所示结果进行对比,不难得出如下结论:应用本文所提定理进行设计的控制器由于考虑了闭环系统二次D-稳定性,对比闭环系统鲁棒H-infinite性能指标与文献[12]中所提算法得到的控制器的相同性能指标,结果有一定的下降,即在相同初始条件下,闭环控制系统(9)在考虑二次D-稳定性的同时使得系统鲁棒性能有一定幅度的下降[13]。
通过图 3、4呈现出来的闭环系统状态响应曲线,不难得出如下结论:随着系统响应时间的不断叠加,分别有不同的系统表现体现在通过本文定理以及文献[12]中所提算法得到的2个闭环控制系统中[14]。从系统调节时间上来看,本文所提定理由于考虑系统二次D-稳定性,导致图 3中曲线首次达到稳态值时所用的调节时间更多,这表明基于文献[12]中所提算法搭建的控制系统在调节速度上更加优秀;将状态曲线第1次达到波峰的2个时间做比较,状态曲线在图 3中表现出良好的上升势头,并且2个波峰之间的时间间隔更短,2个最大值的绝对值之比在稳态时大约为3:1,这也说明图 3中系统状态响应曲线不仅具备足够的稳定裕度,还具有更合理的衰减比;随着系统时间再次叠加且经历过渡过程后,图 3、4中曲线最终所达到的新稳态值与预先期望值之间的误差都保持在相对小的范围内,这充分说明无论是本文定理还是文献[12]中所提算法都可以构造较好调节精度的闭环控制系统;另外,在控制系统超调量指标上,图 3中系统状态响应曲线明显优于图 4中曲线,且拥有更小的最大余差值。至于图 3、4中状态响应曲线的振荡周期和频率方面,图 3中的响应曲线略有优势[15]。
5 结论本文在对陆地自主车系统进行数学建模的基础上,将其归纳为一类广义时滞系统,且考虑该系统具有范数有界形式的参数不确定性。在数值仿真证实所提方法有效性的基础上,得到以下结论:
1) 考虑扰动的此类时滞系统闭环稳定性可以通过求解一组包含参变量的LMIs得到,且系统具有较低的保守性。
2) 在求解该类线性矩阵不等式的过程中,采用广义分段仿射Lyapunov函数、投影定理以及基本引理相结合的方式是可行且有效的。
3) 将运用线性矩阵不等式LMI算法求取鲁棒H-infinite反馈控制器增益矩阵的思想运用到连续时间广义系统,具有一定的优越性。
4) 通过对比以往切换控制算法的实例,证明所提方法具备一定的有效性和卓越性。在存在未知情况下外部干扰和测量噪声时,此类系统滤波器的设计问题将会成为今后广大学者研究的一个热点,对该类系统闭环滤波器同时考虑扰动存在的情况也有待于后续的研究。
| [1] |
MASUBUCHI I, KAMITANE Y, OHARA A, et al. control for descriptor systems:a matrix inequalities approach[J]. Automatica, 1997, 33(4): 669-673. DOI:10.1016/S0005-1098(96)00193-8 ( 0) 0)
|
| [2] |
DE OLIVEIRA M C, GEROMEL J C. A class of robust stability conditions where linear parameter dependence of the Lyapunov function is a necessary condition for arbitrary parameter dependence[J]. Systems & control letters, 2005, 54(11): 1131-1134. ( 0) 0)
|
| [3] |
QIU Jianbin, FENG Gang, GAO Huijun. Approaches to robust static output feedback control of discrete-time piecewise-affine systems with norm-bounded uncertainties[J]. International journal of robust and nonlinear control, 2011, 21(7): 790-814. DOI:10.1002/rnc.v21.7 ( 0) 0)
|
| [4] |
RUBAGOTTI M, TRIMBOLI S, BEMPORAD A. Stability and invariance analysis of uncertain discrete-time piecewise affine systems[J]. IEEE transactions on automatic control, 2013, 58(9): 2359-2365. DOI:10.1109/TAC.2013.2251774 ( 0) 0)
|
| [5] |
EGHBAL N, PARIZ N, KARIMPOUR A. Discontinuous piecewise quadratic Lyapunov functions for planar piecewise affine systems[J]. Journal of mathematical analysis and applications, 2013, 399(2): 586-593. DOI:10.1016/j.jmaa.2012.09.054 ( 0) 0)
|
| [6] |
ZHANG Yu, FENG Gang, SUN Jitao. Stability of impulsive piecewise linear systems[J]. International journal of systems science, 2013, 44(1): 139-150. DOI:10.1080/00207721.2011.598957 ( 0) 0)
|
| [7] |
KAI T, MASUDA R. Limit cycle synthesis of multi-modal and 2-dimensional piecewise affine systems[J]. Mathematical and computer modelling, 2012, 55(3/4): 505-516. ( 0) 0)
|
| [8] |
莫以为, 萧德云. 混合动态系统及其应用综述[J]. 控制理论与应用, 2002, 19(1): 1-8. DOI:10.3969/j.issn.1000-8152.2002.01.001 ( 0) 0)
|
| [9] |
邱剑彬.不确定动态时滞系统的鲁棒滤波设计新方法[D].合肥: 中国科学技术大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10358-2009110999.htm
( 0) 0)
|
| [10] |
周振华.参数不确定广义分段仿射系统的鲁棒控制和滤波[D].哈尔滨: 哈尔滨工业大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10213-1016739453.htm
( 0) 0)
|
| [11] |
RODRIGUES L. Dynamic output feedback controller synthesis for piecewise-affine systems[D]. Palo Alto: Stanford University, 2002. http://www.researchgate.net/publication/234324438_Dynamic_output_feedback_controller_synthesis_for_piecewise-affine_systems
( 0) 0)
|
| [12] |
刘志林.分段仿射系统的控制器设计及预测控制方法研究[D].哈尔滨: 哈尔滨工业大学, 2007: 106-109. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D272468
( 0) 0)
|
| [13] |
胡寿松, 王执铨, 胡维礼. 最优控制理论与系统[M]. 北京: 科学出版社, 2005.
( 0) 0)
|
| [14] |
解学书, 钟宜生. H∞控制理论[M]. 北京: 清华大学出版社, 1994.
( 0) 0)
|
| [15] |
俞立. 鲁棒控制:线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


