相继增压系统可以有效增大发动机低转速时的扭矩以及降低部分负荷时的油耗和排放,但是调速系统在切换过程调速性能不佳会导致发动机产生较大的转速波动,甚至会导致增压器发生喘振,动力性、经济性以及排放性严重恶化[1]。目前大多数调速系统都是基于PID实现的,由于结构简单、稳定性好、工作可靠,PID已经被广泛应用在工业控制过程中[2]。但是,在传统的PID调节过程中由于比例、积分以及微分系数是固定不变的[3],在很多情况下很难确定它们最佳的组合,另外柴油机是一个具有时滞性的复杂的非线性系统[4],在运行过程中会出现转速、负荷以及其他参数的不断变化,所以经典PID控制器无法达到理想的控制效果。
人工神经网络是模拟生物神经系统的组织结构、处理方法以及系统功能的简化系统[5],并以其并行处理、分布式存储、自学习自适应、高度容错等特性而受到广泛关注[6]。目前,神经网络应用于PID控制已经是一大研究热点[7],其中径向基函数(RBF)神经网络以其简单的拓扑结构和全局逼近能力,在模式识别、信号处理、非线性系统的建模和控制等方面得到广泛应用[8]。将神经网络与传统增量式PID相结合形成RBF-PID控制器,利用RBF神经网络非线性映射和自适应学习能力,实现PID控制参数的实时调整[9],能有效改善控制器的控制品质。
为了研究改善TBD620V12相继增压柴油机的瞬态调速性能的方法,本文以目标转速、实际转速、转速偏差以及进气压力作为输入信号建立RBF-PID调速控制系统,并在进行试验之前进行了Simulink与GT-power模型之间的联合仿真计算研究。
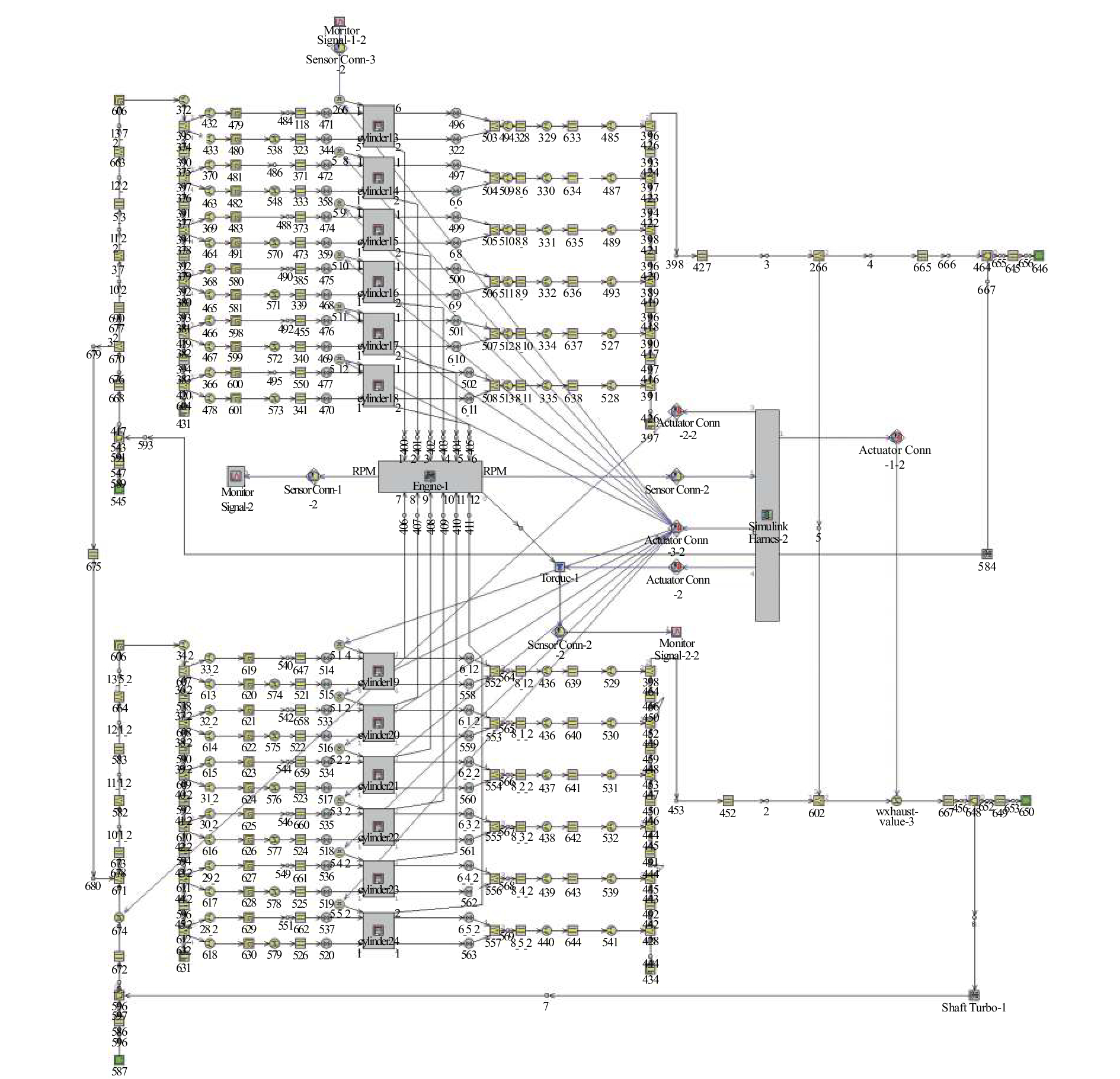
1 TBD620V12 STC柴油机建模及验证为了节约试验成本以及加快STC柴油机调速控制系统改进型产品开发速度,本文在台架试验之前利用GT-power软件建立TBD620V12STC柴油机一维仿真计算模型如图1所示,其中柴油机基本参数如表1所示。
|
Download:
|
| 图 1 TBD620V12STC柴油机一维仿真计算模型 | |
|
|
表 1 TBD620V12STC柴油机基本参数 |
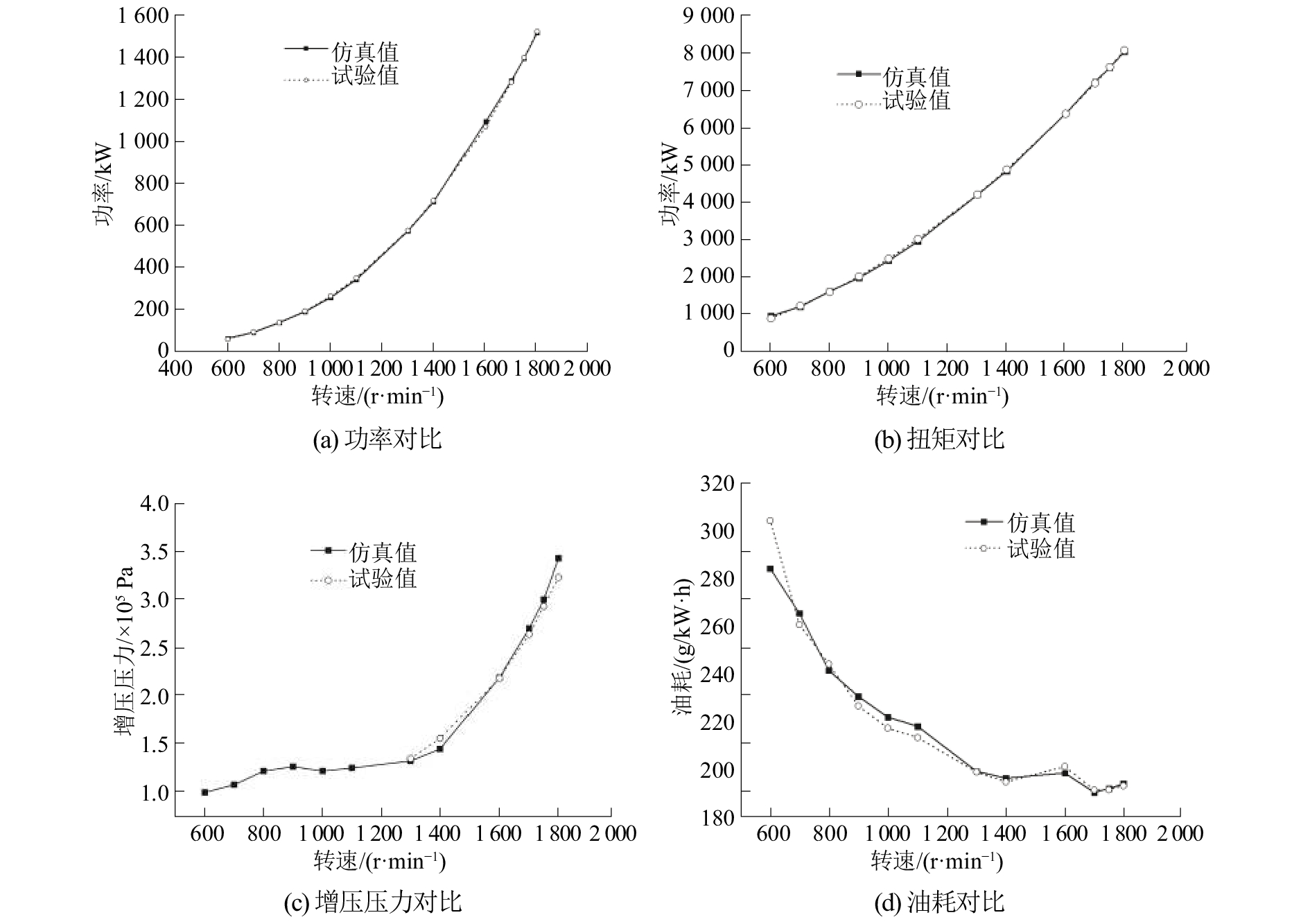
由于受实验数据限制,本文按照螺旋桨特性在2TC状态下选取600、700、800、900、1 000、1 100、1 300、1 400、1 600、1 700、1 750、1 800 r/min这12个工况点进行仿真计算,并将仿真计算得到的功率、扭矩、油耗、增压压力4个参数与实验值进行对比分析,比较结果如图2所示。从图2中可以看出除600 r/min时油耗误差较大,其余工况点有效功率、扭矩、油耗以及增压压力的仿真值与实验值基本吻合,我们近似认为TBD620V12STC柴油机一维仿真模型是准确的,可以进行下一步的仿真计算研究。
|
Download:
|
| 图 2 TBD620V12STC柴油机各项试验值与仿真值对比 | |
PID控制算法种类繁多,其中包括连续系统PID控制算法、离散系统PID控制算法、位置式PID控制算法以及增量式PID控制算法等。其中,增量式PID控制算法具有如下优点:1)控制增量
| $u(k) = u(k - 1) + \Delta u(k)$ |
| $\begin{aligned} \Delta u(k) = &{k_{\rm{P}}}(e(k) - e(k - 1)) + {k_{\rm{I}}}e(k) + {k_{\rm{D}}}(e(k)) - \hfill \\& 2e(k - 1) + e(k - 2)) \hfill \\ \end{aligned} $ |
式中:u(k)、u(k−1)分别为第k、k−1步系统控制量,e(k)、e(k−1)、e(k−2)为第k、k−1、k−2步系统目标值与实际值差值,kP、kI、kD分别为比例、积分和微分系数。
2.2 RBF神经网络模型 2.2.1 网络结构RBF神经网络是一种包含输入层、隐含层和输出层的前向网络[10],输入层由信号源节点组成,输出层对输入层的作用做出响应,隐层单元数视所述问题而定[11]。其网络结构实例如图3所示。

|
Download:
|
| 图 3 RBF神经网络结构 | |
RBF网络结构中,
| $h_j = \exp ( - \frac{{{{(x - c_j)}^2}}}{{2b_j{^2}}}), j = 1,2, \cdots ,m$ |
式中网络第
| ${{C}}_j = {[c_{j_{_1}},c_{j_{_2}}, \cdots ,c_{j_{i}}, \cdots ,c_{j_{n}}]^{\rm{T}}},i = 1,2, \cdots ,n$ |
网络基宽向量为
| ${{B}} = {[b_1,b_2, \cdots ,b_m]^{\rm{T}}}$ |
网络权向量为
| ${{W}} = {[w_1,w_2, \cdots ,w_n]^{\rm{T}}}$ |
辨识网络输出为
| $y_m(k) = w_1h_1 + w_2h_2 + \cdots + w_mh_m$ |
辨识器性能指标函数为
| $J = 0.5{[r(k) - y_m(k)]^2}$ |
式中:r(k)为目标值,
按性能指标函数对加权系数负梯度方向进行搜索调整,并附加使搜索快速收敛的惯性项,输出权、节点中心及节点基宽参数迭代算法如下:
| $\Delta w_j(k) = \theta (r(k) - y_m(k))h_j$ |
| $w_j(k) = w_j(k - 1) + \Delta w_j(k) + \alpha (w_j(k - 1) - w_j(k - 2))$ |
| $\Delta b_j(k) = \theta (r(k) - y_m(k))w_jh_j\frac{{{{\left( {X - C_j} \right)}^2}}}{{b_j{^3}}}$ |
| $b_j(k) = b_j(k - 1) + \Delta b_j + \alpha (b_j(k - 1) - b_j(k - 2))$ |
| $\Delta c_{ji}(k) = \theta (r(k) - y_m(k))w_j\frac{{x_j - c_{ji}}}{{b_j{^2}}}$ |
| $c_{ji}(k) = c_{ji}(k - 1) + \Delta c_{ji}(k) + \alpha (c_{ji}(k - 1) - c_{ji}(k - 2))$ |
式中:
Jacobian阵(对象输出对控制输入变化的灵敏度信息)算法为
| $\frac{{\partial y(k)}}{{\partial \Delta u(k)}} \approx \frac{{\partial y_m(k)}}{{\partial \Delta u(k)}} = \sum\limits_{j = 1}^m {w_jh_j\frac{{c_{ji} - {x_1}}}{{b_j^2}}} $ |
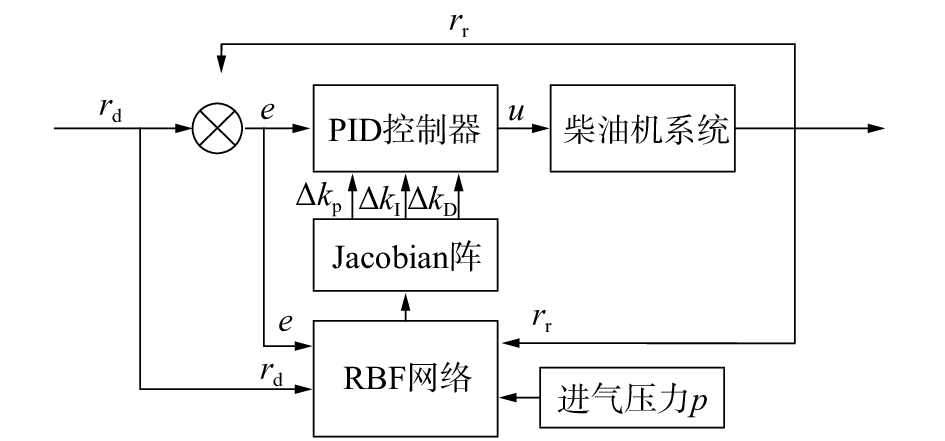
RBF-PID调速控制系统如图4所示,由3部分组成:1)经典增量式PID,对调速系统进行闭环控制;2)RBF网络,在线建立调速系统辨识模型,观测Jacobian灵敏度信息;3)PID参数在线调整,利用RBF网络提供的辨识信息实现参数实时调整,获取最优性能指标。
|
Download:
|
| 图 4 RBF-PID调速控制系统 | |
其中,RBF神经网络对增量式PID控制参数的整定采用梯度下降法,结合2.1、2.2小节以及图4,PID控制参数变化量的计算公式如下:
| $\Delta {k_{\rm{P}}} = - \eta \frac{{\partial E}}{{\partial {k_{\rm{P}}}}} = - \eta \frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial \Delta u}}\frac{{\partial \Delta u}}{{\partial {k_P}}} = \eta e\left( k \right)\frac{{\partial y}}{{\partial \Delta u}}\left( {e\left( k \right) - e\left( {k - 1} \right)} \right)$ |
| $\Delta {k_{\rm{I}}} = - \eta \frac{{\partial E}}{{\partial {k_{\rm{I}}}}} = - \eta \frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial \Delta u}}\frac{{\partial \Delta u}}{{\partial {k_{\rm{I}}}}} = \eta e\left( k \right)\frac{{\partial y}}{{\partial \Delta u}}e\left( k \right)$ |
| $\begin{aligned} \Delta {k_{\rm{D}}} = &- \eta \frac{{\partial E}}{{\partial {k_{\rm{D}}}}} = - \eta \frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial \Delta u}}\frac{{\partial \Delta u}}{{\partial {k_{\rm{D}}}}} = \hfill \\& \eta e\left( k \right)\frac{{\partial y}}{{\partial \Delta u}}\left( {e\left( k \right) - 2e\left( {k - 1} \right) + e\left( {k - 2} \right)} \right) \hfill \\ \end{aligned} $ |
传统的神经网络-PID调速系统选取目标转速、实际转速以及转速偏差作为网络输入,然而STC柴油机在切换过程以及切换之后的加减载过程中进气压力剧烈波动,导致过量空气系数变化较大,柴油机缸内燃烧效率和有效功率输出也极不稳定,进而导致柴油机转速剧烈波动。本文提出了一种改进型的RBF-PID调速控制系统,本文以目标转速rd、实际转速rr、转速偏差e以及进气压力p这4个变量作为RBF神经网络的输入变量,以柴油机转速作为RBF神经网络辨识结果,然后通过RBF神经网络辨识结果计算Jacobian阵,最后通过Jacobian阵可以计算得到比例、积分以及微分系数的变化量进而可以对比例、积分以及微分系数进行实时更新。通过大量仿真计算选取RBF神经网络结构为4-6-1结构,学习速率θ取值0.25,惯性系数α取值0.05。
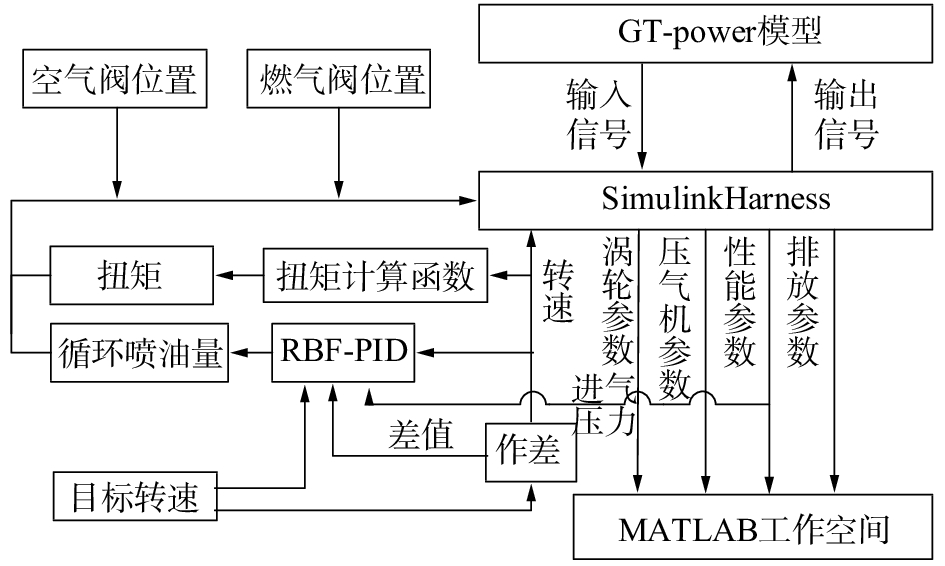
3 GT-power与Simulink联合仿真平台STC柴油机GT-power模型与Simulink控制系统模型进行联合仿真计算是通过GT-power模型中Simulink-Hardness模块以及Simulink模型中的GT-SUITE Model模块联系起来的,其中控制系统模型与STC柴油机模型联合仿真平台简化原理图如图5所示。在GT-power模型中通过传感器(SensorCon)模块采集涡轮参数、压气机参数、排放参数以及柴油机转速等性能参数,并经Simulink-Harness模块传至Simulink模型中,涡轮参数、压气机参数、性能参数以及排放参数则直接输入至MATLAB的工作空间,保存计算结果,而柴油机转速信号、进气压力信号、目标转速信号以及转速误差信号传至RBF-PID调速控制系统模型,并经RBF-PID调速控制系统整定得到每缸每循环喷油量,同时利用转速经扭矩计算函数(螺旋桨特性)计算出实时扭矩,喷油量和扭矩作为输出信号经由Simulink-Harness模块传至GT-power模型中,并经过执行器(ActuatorCon)模块分别施控于喷油模块及加减载模块。
|
Download:
|
| 图 5 联合仿真平台原理 | |
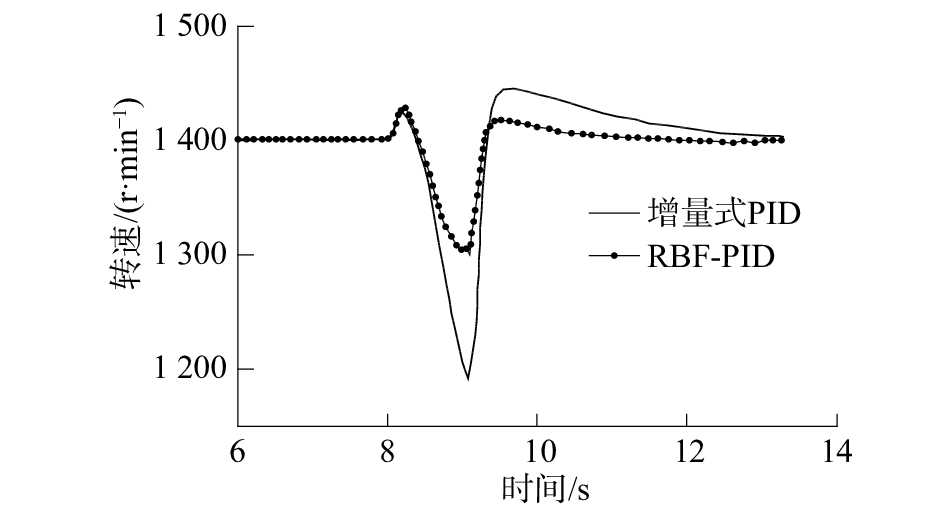
在本次研究之前,通过大量的仿真计算以及试验验证,可以提前得到如下结论:STC柴油机1TC与2TC(1TC代表单独一个涡轮增压器运行,2TC表示2个涡轮增压器并联同时运行)之间的切换点转速选定在1 400 r/min时,柴油机的经济性最优;柴油机运行工况符合标准螺旋桨特性,即扭矩与转速的三次方成比例关系;本文采用1/4衰减曲线法整定得到增量式PID控制参数及RBF-PID调速系统初始控制参数,其分别为:kP=455、kI=0.413、kD=0.020 8,限于篇幅,本文不再进行验证。图6为在传统增量式PID调速系统以及RBF-PID调速系统控制下,STC柴油机从1TC切换至2TC过程的调速效果对比。图7为在RBF-PID调速系统控制下,STC柴油机从1TC切换至2TC过程,RBF-PID调速系统控制参数随时间的变化趋势。
|
Download:
|
| 图 6 1TC切换至2TC过程2种调速系统控制效果对比 | |

|
Download:
|
| 图 7 1TC切换至2TC过程PID参数随时间变化趋势 | |
通过图6可以看出:STC柴油机从1TC切换至2TC过程,当采用经典增量式PID调速系统时,柴油机最高转速为1 445 r/min,最低转速为1 190 r/min,即最大转速波动量为255 r/min;当采用RBF-PID调速系统时,柴油机最高转速为1 426 r/min,最低转速为1 301 r/min,即最大转速波动量为125 r/min。切换过程柴油机在RBF-PID调速系统控制下的最大转速波动量较增量式PID调速系统控制下的最大转速波动量减少130 r/min,降幅为51%。另外,从空气阀开启时刻(8 s)到柴油机转速恢复到1 400 r/min,增量式PID调速系统耗时4.2 s,RBF-PID调速系统耗时3 s,降幅28.6%。
结合图6,通过图7可以看出,RBF-PID调速系统控制参数在STC柴油机切换过程随着柴油机转速变化而变化,总体来说,转速降低,kP、kI、kD值升高,而转速升高,kP、kI、kD值降低。相对于控制参数固定不变的增量式PID调速系统,RBF-PID调速系统能够更加迅速地根据柴油机转速变化调节PID控制参数,进而可以快速地调节柴油机循环喷油量,使STC柴油机在1TC与2TC之间的切换过程调速更加灵活。综合图6、7,可以得出以下结论:RBF-PID调速系统不但能够明显地减小STC柴油机切换过程转速波动,而且能够大大加快速STC柴油机切换过程的稳定速度,极大地改善STC柴油机切换过程的调速品质,进而改善柴油机的经济性和排放性。
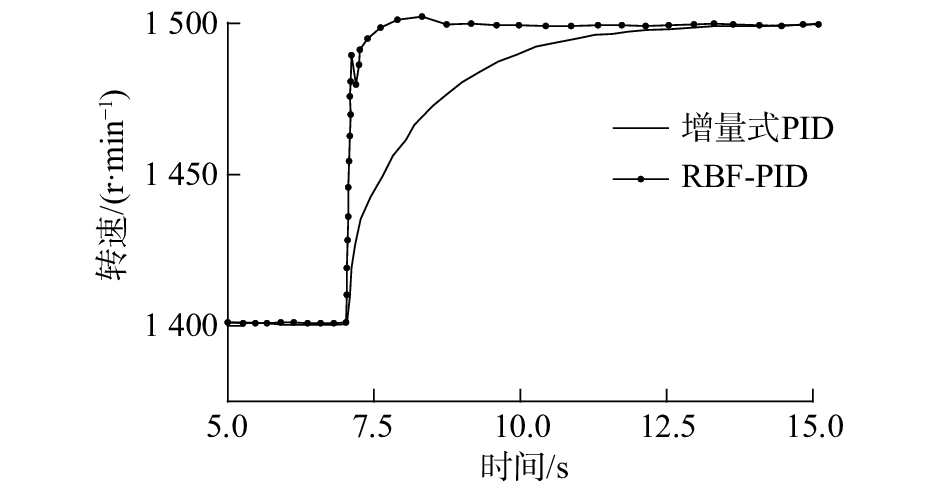
4.2 相继增压柴油机突加速响应仿真结果分析为了对比分析2种调速系统在柴油机突加速情况的调速性能,本文选取在7 s仿真时刻,柴油机目标转速由1 400 r/min突变至1 500 r/min,图8为STC柴油机转速在2种调速系统下的响应曲线。从图中响应过程来看:STC柴油机在增量式PID调速系统控制下的稳定时间为6.2 s,而在RBF-PID调速系统控制下的稳定时间为1.7 s,相比减少了4.5 s,降幅72.6%,而其超调量仅为3 r/min,几乎可以忽略不计。可以看出RBF-PID调速器在柴油机突变速情况下具有更快的稳定速度,能够迅速变化到期望值,且不会产生较大的超调。
|
Download:
|
| 图 8 突加速过程两种调速系统控制效果对比 | |
在STC柴油机切换过程,传统增量式PID调速系统由于比例、积分以及微分系数固定而无法满足其复杂非线性、时变性要求,进而导致切换过程产生较大的转速波动。本文结合RBF神经网络与经典增量式PID调速系统,建立一种具有自适应功能的RBF-PID调速控制系统,经过STC柴油机模型与Simulink控制系统模型的联合仿真计算,可初步得到如下结论:
1)STC柴油机从1TC切换至2TC过程,RBF-PID调速系统控制下的最大转速波动较增量式PID调速系统控制下的转速波动减少了130 r/min,降幅达到51%,且柴油机回归至稳定转速的时间也减少了1.2 s,降幅28.6%,进一步说明了RBF-PID调速系统不但能够明显地减小切换过程转速波动,而且能够加快柴油机转速稳定。
2)STC柴油机突加速响应方面,柴油机在RBF-PID调速系统控制下达到目标转速的稳定时间较增量式PID减少了4.5 s,降幅72.6%,而其超调量仅为3 r/min,进一步论证了RBF-PID调速系统在柴油机突变速情况下具有更快的稳定速度,能够迅速加载到期望值,且不会产生较大的超调。
3)通过对比分析,获得以上良好调速效果的原因是RBF-PID调速系统能够根据柴油机实际转速与目标转速的关系自动调整PID控制算法的比例、积分以及微分系数,使STC柴油机切换过程的调速过程更加灵活、可靠。
| [1] |
王银燕, 于恩程. 相继增压柴油机瞬态切换喷油策略[J]. 哈尔滨工程大学学报, 2012, 33(7): 839-844. DOI:10.3969/j.issn.1006-7043.201107066 ( 0) 0)
|
| [2] |
王永骥, 涂键. 神经元网络控制[M]. 北京: 机械工业出版社, 1998: 303-310.
( 0) 0)
|
| [3] |
夏思为, 段书凯, 王丽丹, 等. 基于忆阻神经网络PID控制器设计[J]. 计算机学报, 2013, 36(12): 2577-2586. ( 0) 0)
|
| [4] |
SHAO Shihuang. Fuzzy self-organizing controller and its application for dynamic processes[J]. Fuzzy sets and systems, 1988, 26(2): 151-164. DOI:10.1016/0165-0114(88)90205-9 ( 0) 0)
|
| [5] |
许焕升. 左右脑与领导力平衡法则[J]. 当代经理人, 2007(5): 110-111. ( 0) 0)
|
| [6] |
胡守仁, 沈清, 胡德文, 等. 神经网络应用技术[M]. 长沙: 国防科技大学出版社, 1995.
( 0) 0)
|
| [7] |
孙增圻. 智能控制理论与技术[M]. 北京: 清华大学出版社, 1997: 125-239.
( 0) 0)
|
| [8] |
乔俊飞, 韩红桂. RBF神经网络的结构动态优化设计[J]. 自动化学报, 2010, 36(6): 865-872. ( 0) 0)
|
| [9] |
屈毅, 宁铎, 赖展翅, 等. 温室温度控制系统的神经网络PID控制[J]. 农业工程学报, 2011, 27(2): 307-311. ( 0) 0)
|
| [10] |
周维华. RBF神经网络隐层结构与参数优化研究[D]. 上海: 华东理工大学, 2014.
( 0) 0)
|
| [11] |
朱逢锐. 基于RBF神经网络的PID自校正控制研究及应用[D]. 淮南: 安徽理工大学, 2017.
( 0) 0)
|
| [12] |
李广军. 基于RBF神经网络的PID整定[D]. 成都: 西南交通大学, 2005.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


