出于对安全性和经济性的综合考虑,破前漏(leak before break,LBB)思想在压水堆核电厂的设计中逐渐受到重视[1-2]。破前漏技术主要包括裂纹扩展机制、裂纹极限断裂尺寸以及贯穿裂纹泄漏率分析等。通过检测贯穿裂纹泄漏率可以确定裂纹尺寸,从而确定管道的安全裕量,因此泄漏率分析对于破前漏技术的应用至关重要[3]。
1984年由美国电力研究院发起的PICEP项目对LEAK-01程序进行了修正,基于Henry均相非平衡临界流模型,形成可用于预测裂纹泄漏率的程序PICEP。此后,美国核管会通过IPIRG项目资助了管道泄漏相关研究,开发出用于预测管道泄漏率的SQUIRT程序。SQUIRT程序使用Henry-Fauske临界流理论,考虑了液体流过裂纹时的非均匀相变过程[4]。随着我国核电发展对相关技术的需求,国内相关单位开展了一系列关于泄漏率预测的研究,形成了诸如PICLES、CLR和COLROPC等程序[5-8]。由于贯穿裂纹内的临界流动特性及其不规则形状对裂纹流道内的流体流动有直接影响,也决定了泄漏率的大小,然而关于其影响关系尚缺乏深入分析。
为了分析裂纹几何形貌对泄漏率的影响,结合裂纹流道流动特性数值模拟分析结果,开发用于压水堆核电厂管道贯穿裂纹泄漏率的计算程序,并与矩形窄缝和应力腐蚀裂纹泄漏实验数据进行对比。分析压降组成比例以明确裂纹几何形貌的影响机理,基于计算程序分析不同参数对泄漏率的影响。
1 泄漏率计算模型贯穿裂纹泄漏率主要受裂纹流道内的流体热工状态、裂纹几何形状以及裂纹尺寸影响。一方面,压水堆内的高温高压流体会在裂纹流道内形成临界流动;另一方面,裂纹流道内部的锯齿结构会对泄漏流体流动造成影响。下面从临界流动和贯穿裂纹阻力特性两方面开展模型研究,构建压水堆管道贯穿裂纹泄漏率计算分析的基础。
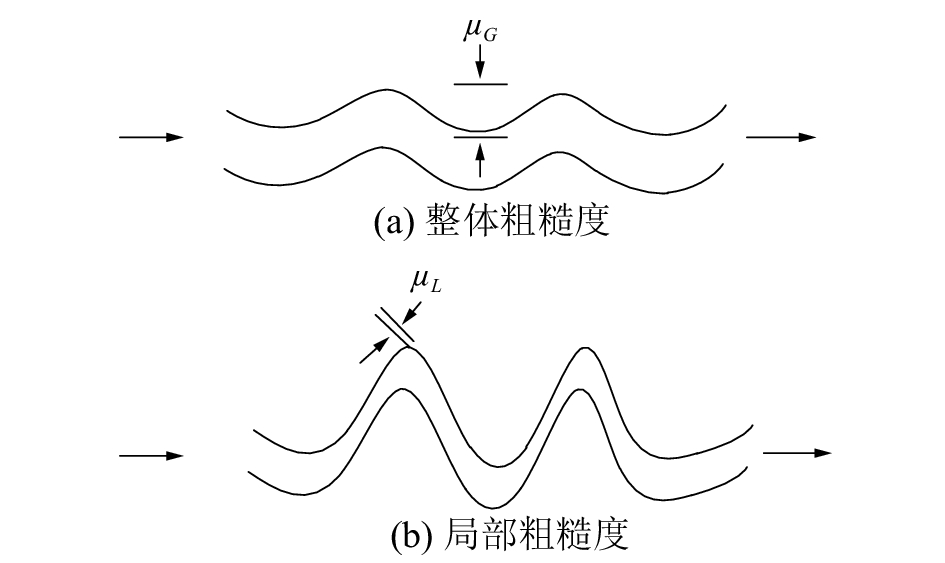
1.1 裂纹几何形貌描述在很多情况下,裂纹的截面形状可以假定为锯齿形,这种锯齿形会影响流体的摩擦压降和裂纹有效长度。裂纹截面复杂的形状会对流道的粗糙度产生影响,这涉及到裂纹面整体粗糙度和局部粗糙度的概念,整体粗糙度主要由流道中存在的弯折所致,而局部粗糙度则是由流道面上的不平整造成,如图 1所示。
|
Download:
|
| 图 1 裂纹面总体粗糙度和局部粗糙度 | |
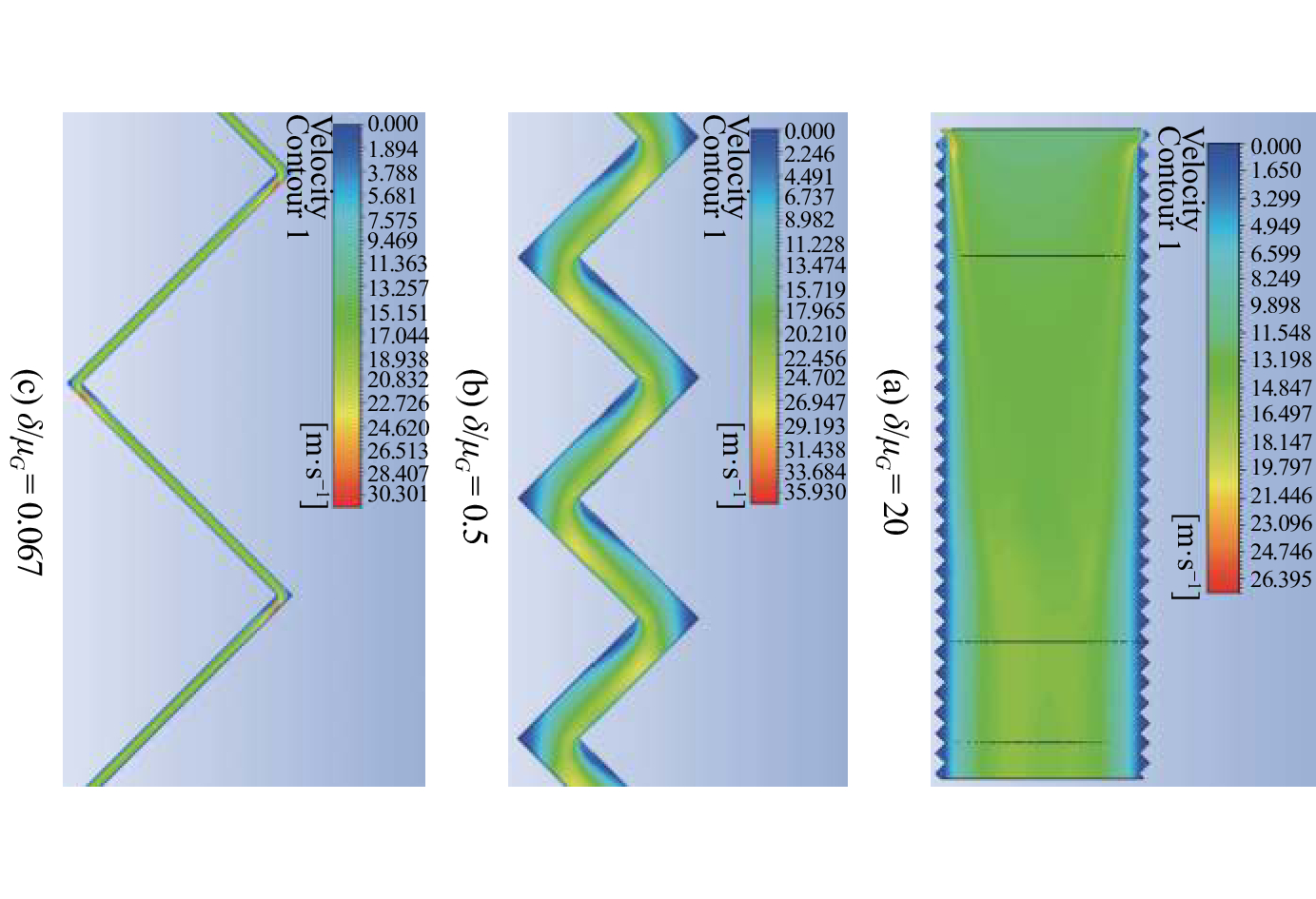
假定裂纹内的弯折对称且均匀,构建裂纹流道几何模型,并对流体域网格进行划分,计算裂纹流道内的流场分布特性。计算湍流模型为标准k-ε模型,入口边界条件为速度边界,流道出口边界条件为压力出口边界,壁面局部粗糙度设定为20 μm。不同宏观粗糙度条件下获得的裂纹流道流场分布如图 2所示。当宏观粗糙度远小于裂纹宽度时(即如图 2(a)所示),裂纹表面的锯齿形突起对流体流场影响不大,通道的形状不会对流体流向产生影响。随着宏观粗糙度的逐渐增加,裂纹内的弯折逐渐对通道内的流动产生影响(如图 2(b)所示),但是此时流体速度方向并未完全改变,对阻力的影响也小一些。当宏观粗糙度增大到一定程度之后,裂缝内流道成为具有多个拐弯的窄通道(如图 2(c)所示),从图中可以看出流体在通道转弯处完全转向,单独一段直通道的流动完全发展,转弯处流体速度变化比较剧烈。随着裂纹宏观粗糙度的进一步增加,由裂纹转弯所导致的流体入口段和出口段所占份额逐渐减小,转弯所导致的局部阻力损失份额也会减小。
|
Download:
|
| 图 2 裂纹流道内速度分布 | |
裂纹有效粗糙度(μ)取决于裂纹张开位移(δ)、裂纹面整体粗糙度(μG)与局部粗糙度(μL),裂纹有效粗糙度用于流体阻力的计算,有效粗糙度的大小为
| $\mu = \left\{ \begin{array}{l}{\mu _L},\;0 < \displaystyle\frac{\delta }{{{\mu _L}}} < 0.1\\{\mu _L} +V \displaystyle\frac{{{\mu _G} - {\mu _L}}}{{4.9}}\left( {\displaystyle\frac{\delta }{{{\mu _L}}} - 0.1} \right),\;0.1 < \frac{\delta }{{{\mu _L}}} < 5\\{\mu _G},\;\displaystyle\frac{\delta }{{{\mu _L}}} > 5\end{array} \right.$ |
与总体粗糙度相类似,变向次数也受裂纹张开位移、局部裂纹变向数ntL等因素的影响,具体计算为
| ${n_t} = \left\{ \begin{array}{l} {n_{tL}},\;0 <\displaystyle \frac{\delta }{{{\mu _L}}} < 0.1 \hfill \\ {n_{tL}} + \displaystyle\frac{{{n_{tL}}}}{{4.9}}\left( {\frac{\delta }{{{\mu _L}}} - 0.1} \right),\;0.1 < \frac{\delta }{{{\mu _L}}} < 5 \hfill \\ 0,\;\displaystyle\frac{\delta }{{{\mu _L}}} > 5 \hfill \\ \end{array} \right.$ |
对于长流道内的两相临界流动,两相流体之间能够达到热力平衡,但是速度差异比较大,而且应当考虑管壁的摩擦效应。Fauske从动量方程出发,考虑了管壁的摩擦效应,在等焓过程假定条件下,导出了临界流量的计算关系式。在上述研究的基础上,Henry根据其空泡份额实验,计算出两相系统滑速比随含气率减少而减少,并认为低含气率的单组分两相临界流动接近均相流动,可以忽略滑移效应,但必须考虑热力不平衡的影响[9]。流动流体的蒸发率低于维持热力平衡所需的蒸发率,蒸汽处于当地压力下的饱和状态、液体处于过热状态。Henry[10-11]运用分相流动动量方程,结合dG/dp=0的条件,求出下面临界流量的计算式:
| $G_c^2 = {\left[ {\frac{{x{v_g}}}{{\gamma p}} - \left( {{v_g} - {v_l}} \right)N\frac{{{\rm{d}}{x_e}}}{{{\rm{d}}p}}} \right]^{ - 1}}$ | (1) |
式中:x为含气率,νg为气相比容,νl为液相比容,p为压力,Gc为裂纹出口的临界质量流量,N为偏离平衡含气率xe的量度,γ为等熵膨胀系数,式(1)也称为Henry-Fauske关系式,常用于裂纹泄漏率预测计算。
非平衡含气率x可由式(2)计算:
| $x = N{x_e}\left\{ {1 - \exp \left[ { - B\left( {L/{D_{\rm{H}}} - 12} \right)} \right]} \right\}$ | (2) |
式中:
| $N = \left\{ \begin{aligned}& 20{x_e} ,\;{x_e} < 0.05 \\& 1.0 ,\;{x_e} \geqslant 0.05 \\ \end{aligned} \right.$ |
常数B等于0.523,L为流道的长度,DH为水力直径。
1.3 贯穿裂纹流体流动阻力模型裂纹发生泄漏之后流道内的压降计算为
| ${p_o} - {p_c} = {p_e} + {p_a} + {p_f} + {p_k} + {p_{aa}}$ | (3) |
式中:下标o和c分别代表裂纹入口和裂纹出口处的参数,压降主要包括入口压降pe、相变加速压降pa、摩擦压降pf、弯曲和突起引起的局部压降pk和面积变化引起的加速压降paa。
入口压降损失pe为
| ${p_e} = \frac{{G_o^2{v_{lo}}}}{{2C_D^2}}$ |
式中:Go为入口质量流量,νlo为入口液相比容,CD为入口突变系数,对于裂纹张开位移小于0.15 mm的窄裂缝CD取0.95,对于较大的裂缝,该值处于0.62~0.95,本研究取0.95。
摩擦压降pf为
| ${p_f} = \left( {f\frac{L}{{{D_H}}}} \right)\frac{{G_c^2}}{2}\left[ {\left( {1 - \bar x} \right){{\bar v}_l} + \bar x\;{{\bar v}_g}} \right]$ | (4) |
式中:f为摩阻系数,x为含气率,“ˉ”表示平均值。根据L/DH的大小可将流道分为2段,L/DH>12时处于汽液两相区域,0<L/DH<12对应于单相液区。式(4)可进一步写为
| ${p_f} = f\left( {\frac{L}{{{D_H}}} - 12} \right)\frac{{G_c^2}}{2}\left[ {\left( {1 - \bar x} \right){{\bar v}_l} + \bar x\;{{\bar v}_g}} \right] + 12f\frac{{{{\bar G}_o}^2}}{2}{v_{lo}}$ |
由于存在下述关系:
| ${A_o}{G_o} = {A_c}{G_c}$ |
式中:Ao为入口截面面积,Ac为出口截面面积。
因此可进一步得出摩擦阻力为
| ${p_f} = f\left( {\frac{L}{{{D_H}}} - 12} \right)\frac{{G_c^2}}{2}\left[ {\left( {1 - \bar x} \right){{\bar v}_l} + \bar x\;{{\bar v}_g}} \right] + 6f{\left( {\frac{{{A_c}}}{{{A_o}}}} \right)^2}G_o^2{v_{lo}}$ |
基于PRAISE程序,摩阻系数的计算为
| $f = {\left[ {{C_1}\log \left( {\frac{{{D_H}}}{{2\mu }}} \right) + {C_2}} \right]^{ - 2}}$ |
式中:μ为壁面粗糙度,在应力腐蚀裂纹(stress corrosion cracking,SCC)生长时为6.2 μm,在疲劳裂纹生长时为40 μm。当DH/2μ≤27.74时C1和C2分别为3.39和0.86,当DH/2μ>27.74时C1和C2分别为2和1.74。
窄裂缝中的流动摩擦系数的选取对于泄漏率分析非常重要,最常用于泄漏率分析的关系式由Von Karman关系式修改得到:
| $\begin{array}{l}f = {\left[ {{C_1}\log \left( {{D_{\rm{H}}}/\left( {2k} \right)} \right) + {C_2}} \right]^{ - 2}} = \\\;\;\;\;\;\;\;\;\left[ {{C_1}\log \left( {{D_{\rm{H}}}/k} \right) + {C_2} - {C_1}\log 2} \right]\end{array}$ |
式中:k是壁面粗糙度、DH是水力直径。对于圆管内的流动而言,C1、C2和DH分别为2、1.74和管道内径。对于非圆管而言,水力直径为
| ${D_{\rm{H}}} = \frac{{4 \times {\text{面积}}}}{{\text{湿周}}}$ |
尽管上述关系式由一些研究者进行了验证[7-8],但是所测试的管道裂纹形状都与圆形截面几何特征有明显区别。对于窄裂缝中的流动而言,截面形状与圆形差别很大,而且等效水力直径方法也会失效。
裂纹流道内的弯曲和突起所贡献的局部阻力为
| ${p_k} = \left( {{e_v}} \right)\frac{{G_c^2}}{2}\left[ {\left( {1 - \bar x} \right){{\bar v}_l} + \bar x\;{{\bar v}_g}} \right]$ |
式中ev为裂纹流道内的总局部压降损失系数,由实验结果得出,即
| ${e_v} = e\left[ L \right]$ |
式中e为给定形式裂纹流道单位长度上的速度头损失次数,在周向焊接疲劳裂纹实验中得出e=6,对于SCC生长实验而言e=3。
| $\overline G = \frac{{{A_o}{G_o} + {A_c}{G_c}}}{{{A_o} + {A_c}}}$ |
相变加速压降pa为
| ${p_a} = \overline G{_T^2}\left[ {\left( {1 - {x_c}} \right){v_{lc}} + {x_c}{v_{gc}} - {v_{lo}}} \right]$ |
式中
由面积变化引起的加速压降paa的计算为
| $\begin{array}{l}{p_{aa}} = \displaystyle\frac{{G_c^2{v_{lo}}}}{2}\left[ {{{\left( {\frac{{{A_c}}}{{{A_i}}}} \right)}^2} - {{\left( {\displaystyle\frac{{{A_c}}}{{{A_o}}}} \right)}^2}} \right] + \\ \;\;\;\;\;\;\;\;\;\displaystyle\frac{{G_c^2}}{2}\left[ {\left( {1 - x} \right){v_{lc}} + x{v_{gc}}} \right] \times \left[ {1 - {{\left( {\frac{{{A_c}}}{{{A_i}}}} \right)}^2}} \right] \\ \end{array}$ |
式中:Ai为两相流动起始点处的界面面积,即L/DH =12处;泄漏率计算过程中可认为截面面积为常数,因此Go=Gc且paa为零。
2 泄漏率计算流程联立式(1)和(3)可以得到泄漏率计算控制方程组,此方程组为非线性方程组,需要采用迭代的方式进行求解,以临界质量流速和临界压力为未知参数,式(1)和(3)可以写为
| $\mathit{\Phi }\left( {G_c^2,{p_c}} \right) = G_c^2 - \left[ {\frac{{{x_c}{v_{gc}}}}{{\gamma {p_c}}} - \left( {{v_{gc}} - {v_{lc}}} \right)N\frac{{{\rm{d}}{x_E}}}{{{\rm{d}}p}}} \right]_c^{ - 1}$ |
| $\mathit{\Omega }\left( {G_c^2,{p_c}} \right) = \Delta {p_{co}} + G_c^2\left( {{B_{{p_e}}} + {B_{{p_a}}} + {B_{{p_f}}} + {B_{{p_k}}} + {B_{{p_{aa}}}}} \right)$ |
式中
| ${B_{{p_e}}} = \frac{{{v_{lo}}}}{{2C_D^2}}$ |
| ${B_{{p_a}}} = \left( {1 - {x_c}} \right){v_{lc}} + {x_c}{v_{gc}} - {v_{lo}}$ |
| ${B_{{P_f}}} = \frac{f}{2}\left( {\frac{L}{{{D_H}}} - 12} \right)\left[ {\left( {1 - \bar x} \right){{\bar v}_l} + \bar x\;{{\bar v}_g}} \right] + 6f{\left( {\frac{{{A_c}}}{{{A_o}}}} \right)^2}{v_{lo}}$ |
| ${B_{{P_k}}} = \frac{{\left( {{e_v}} \right)}}{2}\left[ {\left( {1 - \bar x} \right){{\bar v}_l} + \bar x\;{{\bar v}_g}} \right]$ |
| $\begin{array}{l}{B_{{P_{aa}}}} = \displaystyle\frac{{{v_{lo}}}}{2}\left[ {{{\left( {\frac{{{A_c}}}{{{A_i}}}} \right)}^2} - {{\left( {\frac{{{A_c}}}{{{A_o}}}} \right)}^2}} \right] + \displaystyle\frac{{\left[ {\left( {1 - x} \right){v_{lc}} + x{v_{gc}}} \right]}}{2} \times \left[ {1 - {{\left( {\displaystyle\frac{{{A_c}}}{{{A_i}}}} \right)}^2}} \right] \\ \end{array}$ |
对上述问题使用Newton-Raphson方法进行迭代求解,迭代过程中首先假定一个pc;进一步由压降方程迭代求出Gc,将Gc代入临界流动方程,迭代求解得出新的pc;进一步返回到压降方程,进一步迭代,直至求出压降方程和临界流动方程的解,迭代方程为
| ${\left[ {G_c^2} \right]_{n + 1}} = {\left[ {G_c^2} \right]_n} + {h_G}$ |
| ${\left[ {{p_c}} \right]_{n + 1}} = {\left[ {{p_c}} \right]_n} + {h_p}$ |
式中:
| ${h_G} = - \left| {\begin{array}{*{20}{c}}{{\mathit{\Phi }_n}}&{{{\left( {\displaystyle\frac{{\partial \mathit{\Phi }}}{{\partial {p_c}}}} \right)}_n}}\\{{\mathit{\Omega }_n}}&{{{\left( {\displaystyle\frac{{\partial \mathit{\Omega }}}{{\partial {p_c}}}} \right)}_n}}\end{array}} \right|/{\left( {\displaystyle\frac{{\partial \left( {\mathit{\Phi },\mathit{\Omega }} \right)}}{{\partial \left( {G_c^2,{p_c}} \right)}}} \right)_n}$ |
| ${h_p} = - \left| {\begin{array}{*{20}{c}}{{{\left( {\displaystyle\frac{{\partial \mathit{\Phi }}}{{\partial G_c^2}}} \right)}_n}}&{{\mathit{\Phi }_n}}\\{{{\left( {\displaystyle\frac{{\partial \mathit{\Omega }}}{{\partial G_c^2}}} \right)}_n}}&{{\mathit{\Omega }_n}}\end{array}} \right|/{\left( {\frac{{\partial \left( {\mathit{\Phi },\mathit{\Omega }} \right)}}{{\partial \left( {G_c^2,{p_c}} \right)}}} \right)_n}$ |
关于Φ和Ω的Jacobian矩阵定义为
| ${\left. {\frac{{\partial \left( {\mathit{\Phi },\mathit{\Omega }}\right)}}{{\partial \left( {G_c^2,{p_c}} \right)}}} \right|_n} = {\left[ {\frac{{\partial \mathit{\Phi }}}{{\partial G_c^2}}\frac{{\partial \mathit{\Omega }}}{{\partial {p_c}}} - \frac{{\partial \mathit{\Phi }}}{{\partial {p_c}}}\frac{{\partial \mathit{\Omega }}}{{\partial G_c^2}}} \right]_n}$ |
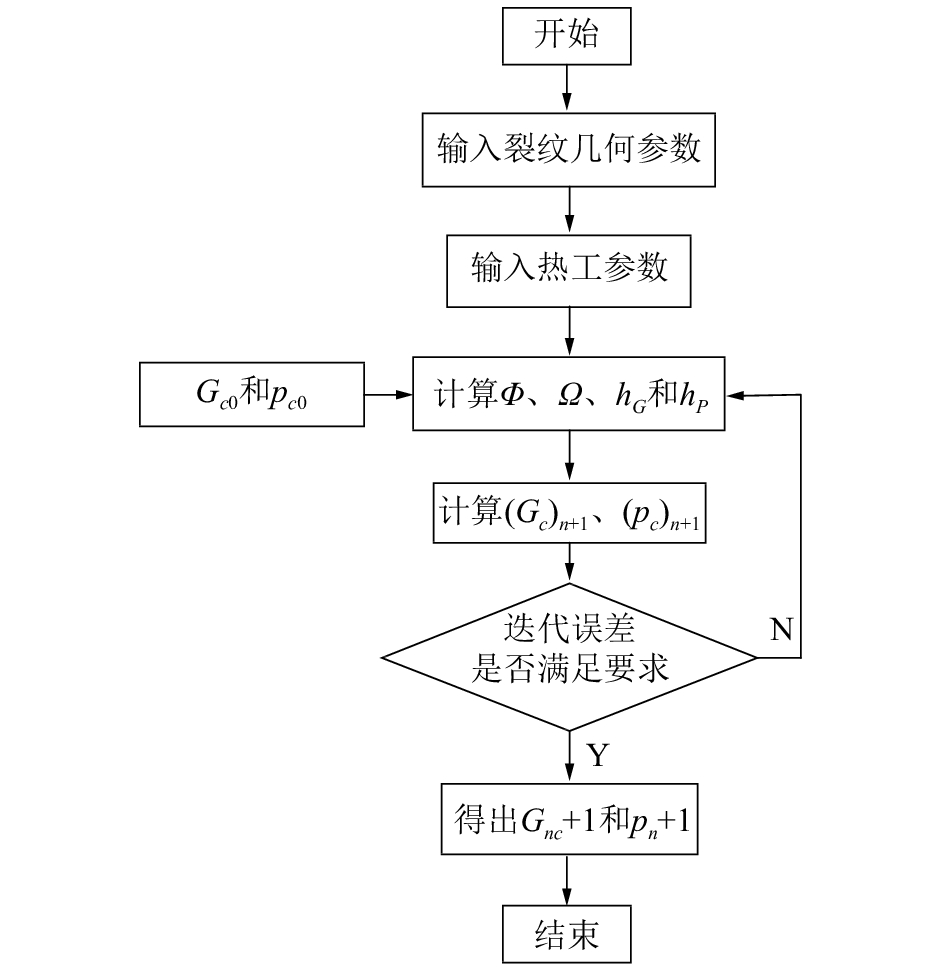
基于上述算法在MATLAB平台编制程序对泄漏率进行计算,计算流程如图 3所示。首先根据裂纹的几何参数和泄漏时的热工参数确定计算输入条件,然后假定迭代初始值,根据前面的关系式计算临界流方程和流动阻力方程中的系数,代入到迭代方程中计算得出新的临界流流量和临界压力,当迭代误差不满足要求时继续迭代,直到满足要求后终止计算。
|
Download:
|
| 图 3 泄漏率计算流程 | |
为了对本文研究的贯穿裂纹泄漏率计算程序进行验证,选取实验数据与计算值进行对比。首先选择矩形窄缝实验结果进行分析,如图 4所示。实验数据来源于Amos的实验[12],通道长度为63.5 mm,裂纹张开位移(crack opening displacement, COD)的大小范围在0.08~0.38 mm。从图 4中可以看出,裂纹泄漏率的计算值与实验值之间的相对误差小于30%。图 4同时给出了SCC泄漏率的实验值和计算值的对比分析结果。实验数据来源于Collier的实验[13],裂纹深度为17.3 mm,表面粗糙度为0.017 8 mm。从图 4中可以看出,本文对应力腐蚀裂纹的泄漏率的预测误差同样在30%内。

|
Download:
|
| 图 4 裂纹泄漏率计算值与实验值的对比 | |
为了研究不同裂纹几何参数对泄漏率的影响,本文基于获得的泄漏率分析程序开展敏感性分析。研究壁面厚度、裂纹宽度、宏观粗糙度、单位长度拐角数量、流体压力以及流体过冷度对临界流泄漏率的影响。选取的基准工况中临界压力为3.549 MPa,流体温度为222.8 ℃,过冷度为20.6 ℃,管道厚度为17.3 mm,COD大小为0.041 5,裂纹宽度为1.59 mm。
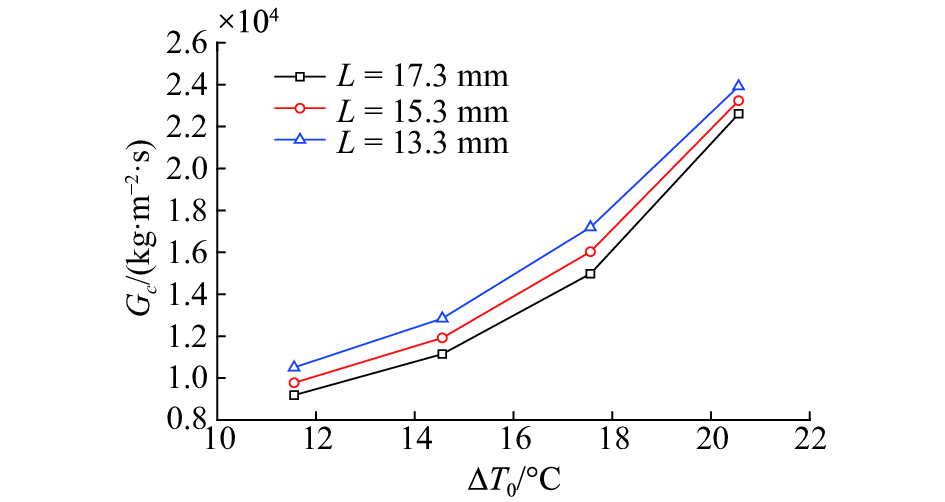
图 5为壁面厚度和流体过冷度对裂纹泄漏率的影响。从图中可以看出,随着入口过冷度的增加,泄漏率会随之增加,这主要是因为过冷度增加之后,两相产汽位置有所滞后,由此造成的流动阻力会相应减小,进一步导致泄漏率有所增加。与此类似,壁面厚度增加之后,流体流过的通道长度会增加,进而导致泄漏率减小。
|
Download:
|
| 图 5 壁面厚度和过冷度对泄漏率的影响 | |
宏观粗糙度和裂纹宽度对泄漏率的影响如图 6所示。由图可见,本研究范围内裂纹宽度的增加、宏观粗糙度的减小都会使裂纹泄漏率增加。这是因为裂纹宽度增加之后裂纹流道截面积也增大,这意味着L/D会变小,流动过程中的摩擦损失减低,导致破口泄漏率增加。宏观粗糙度的减小同样会引起流动摩擦损失的减低,进一步引起破口泄漏率增加。

|
Download:
|
| 图 6 宏观粗糙度和裂纹宽度对泄漏率的影响 | |
图 7为窄缝内拐角数量和流体压力对裂纹泄漏率的影响分析结果,从图中可以看出单位长度拐角数量的增加会导致泄漏率减低,而流体压力的增加会使得泄漏率有所增加。拐角数量的增加会导致压力损失增加,进而造成泄漏率的减低。

|
Download:
|
| 图 7 单位长度拐角和流体压力对泄漏率的影响 | |
本文通过开展贯穿裂纹泄漏率研究,得到以下结论:
1)建立压水堆核电厂运行工况下安全系统检测到的泄漏流量与贯穿裂纹几何尺寸的对应关系,形成了适应于压水堆核电厂核级管道贯穿裂纹的工质泄漏率计算分析方法。
2)经过与矩形窄缝裂纹和应力腐蚀裂纹泄漏率实验对比,本文所得的计算程序对于裂纹泄漏率的预测偏差小于30%。
3)基于获得的计算程序,研究不同参数(包括管道厚度、宏观粗糙度、裂纹拐角数量、流体压力、过冷度)对泄漏率的影响,对于压水堆核电厂管道贯穿裂纹泄漏率分析具有指导意义。
| [1] |
IAEA. Assessment and management of ageing of major nuclear power plant components important to safety primary piping in PWRs[R]. Vienna: IAEA, 2003.
( 0) 0)
|
| [2] |
周胜, 张征明. 破前漏分析中泄漏率模型研究进展[J]. 原子能科学技术, 2009, 43(S1): 84-91. ( 0) 0)
|
| [3] |
WANG Mingjun, QIU Suizheng, SU Guanghui, et al. Research on the leak-rate characteristics of leak-before-break (LBB) in pressurized water reactor (PWR)[J]. Applied thermal engineering, 2014, 62(1): 133-140. DOI:10.1016/j.applthermaleng.2013.08.046 ( 0) 0)
|
| [4] |
PAUL D D, AHMAD J, SCOTT P M, et al. Evaluation and refinement of leak-rate estimation models. NUREG/CR-5128[R]. Washington: Nuclear Regulatory Commission, 1991.
( 0) 0)
|
| [5] |
吴万军, 谢海, 兰彬, 等. 管道裂纹泄漏率计算软件开发[J]. 核动力工程, 2015, 36(4): 65-68. ( 0) 0)
|
| [6] |
殷海峰, 梁兵兵, 徐宁. 管道泄漏率计算模型研究和程序开发[J]. 核技术, 2013, 36(4): 040618. ( 0) 0)
|
| [7] |
乔红威, 李琦, 刘志伟, 等. LBB设计中管道贯穿裂纹张开位移及泄漏率计算研究[J]. 核技术, 2013, 36(4): 040619. ( 0) 0)
|
| [8] |
章静, 乔红威, 李朋洲, 等. 管道贯穿裂纹泄漏率预测[J]. 原子能科学技术, 2015, 49(4): 660-666. ( 0) 0)
|
| [9] |
PARK J H, CHO Y K, KIM S H, et al. Estimation of leak rate through circumferential cracks in pipes in nuclear power plants[J]. Nuclear engineering and technology, 2015, 47(3): 332-339. DOI:10.1016/j.net.2014.11.008 ( 0) 0)
|
| [10] |
HENRY R E. Critical discharge of initially saturated or subcooled liquid[R]. Cleveland: Lewis Research Center, 1969.
( 0) 0)
|
| [11] |
HENRY R E, FAUSKE H K, MCCOMAS S T. Two-phase critical flow at low qualities. Part I. experimental[R]. Argonne: Argonne National Laboratory, 1970.
( 0) 0)
|
| [12] |
AMOS C N, SCHROCK V E. Critical discharge of initially sub-cooled water through slits. NUREG/CR-3475[R]. Berkeley: Lawrence Berkeley Lab, 1983.
( 0) 0)
|
| [13] |
COLLIER R P, STULEN M E, MAYFIELD D B, et al. Two-phase flow through intergranular stress corrosion cracks and resulting acoustic emission. NP-3540-LD[R]. Battelle, Columbus, USA: EPRI Report, 1984.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


