由于我国各地电能消费比重和电力需求不断上涨，直流输电工程^[1]发展前景良好。在直流输电过程中，随着输电等级不断升高，导线周围场强也随之增大，附近的空气会电离造成电晕放电，离子往返运动即形成电晕电流^[2]。电晕放电造成电能损耗、可听噪声、电磁干扰等一系列环境问题^[3]，通过对电晕电流有效监测能保证输电线路安全运行。

为了深入研究输电线路电磁干扰及电晕损耗，首先需对电晕电流信号进行建模。P. Sarma Maruvada等^[4]采集了多种电晕电流信号，提出用双指数函数对电晕电流波形进行建模拟合。樊高辉、刘尚合等^[5]对电晕电流建立BP神经网络模型，对3种实测信号建立统一表达式。但随着输电电压等级的升高，实测的信号带有较大的噪声干扰^[6]，无法用简单的数学模型进行拟合。本文针对电晕电流信号的建模问题，采用了时间序列分析的方法，对电晕电流时间序列建立求和自回归积分滑动平均(ARIMA)模型，能有效对实测信号进行拟合，同时对短期电晕电流信号进行预测。

1 时间序列分析 1.1 自回归滑动平均(autoregressive integrated moving average，ARMA)模型

假设时间序列 ${x_1},{x_2}, \cdots ,{x_t}$ 存在扰动 ${\varepsilon _1},{\varepsilon _2}, \cdots ,{\varepsilon _t}$ ，如果时刻t对应的值x_t不仅与以前的值 ${x_{t - 1}},{x_{t - 2}}, \cdots $ 有关，还与以前时刻对应的扰动 ${\varepsilon _{t - 1}},{\varepsilon _{t - 2}}, \cdots $ 存在一定关联^[7]，那么满足该情况的模型称为ARMA模型。ARMA(p, q)可表示为

${x_t} = \mathop \sum \limits_{i = 1}^p {\phi _i}{x_{t - i}} - \mathop \sum \limits_{j = 1}^q {\theta _j}{\varepsilon _{t - j}} + {\varepsilon _t}$

(1)

为保证式中最高阶数为p和q， ${\phi _p} \ne 0$ 且 ${\theta _q} \ne 0$ ，随机干扰项ε_t满足 $E({\varepsilon _t}) = 0$ ， ${\rm{Var}}({\varepsilon _t}) = \sigma _\varepsilon ^2$ ，且对于 $\forall s \ne t$ ， $E({\varepsilon _s}{\varepsilon _t}) = 0$ ^[8]。

引入延迟算子，式(1)可简记为

$\varPhi \left( B \right){x_t} = \varTheta \left( B \right){\varepsilon _t}$

式中： $\varPhi \left( B \right) = \left( {1 - {\phi _1}B - {\phi _2}{B^2} - \cdots - {\phi _p}{B^p}} \right)$ ， $\varPhi \left( B \right)$ 为自回归系数多项式； $\varTheta \left( B \right) = \left( {1 - {\theta _1}B - {\theta _2}{B^2} - \cdots - {\theta _q}{B^q}} \right)$ ， $\varTheta \left( B \right)$ 为移动平均系数多项式。

ARMA(p, q)模型中，当q=0时，即为AR(p)模型；当p=0时，即为MA(q)模型。

1.2 求和自回归积分滑动平均(ARIMA)模型

ARIMA(p, d, q)模型具有如下结构：

$\varPhi \left( B \right){\nabla ^d}{x_t} = \varTheta \left( B \right){\varepsilon _t}$

式中：随机干扰项ε_t满足 $E({\varepsilon _t}) = 0$ ， ${\rm{Var}}({\varepsilon _t}) = \sigma _\varepsilon ^2$ ，且对于 $\forall s \ne t$ ， $E({\varepsilon _s}{\varepsilon _t}) = 0$ 。 ${tnabla ^d} = {\left( {1 - B} \right)^d}$ ，表示进行d阶差分， $\varPhi \left( B \right)$ 为ARMA模型的自回归系数多项式， $\varTheta \left( B \right)$ 为对应的移动平均系数多项式。

ARIMA模型实际上是ARMA模型与差分运算的结合。对非平稳信号进行差分处理，将其转化为平稳信号，后对平稳信号建立ARMA模型^[9]。

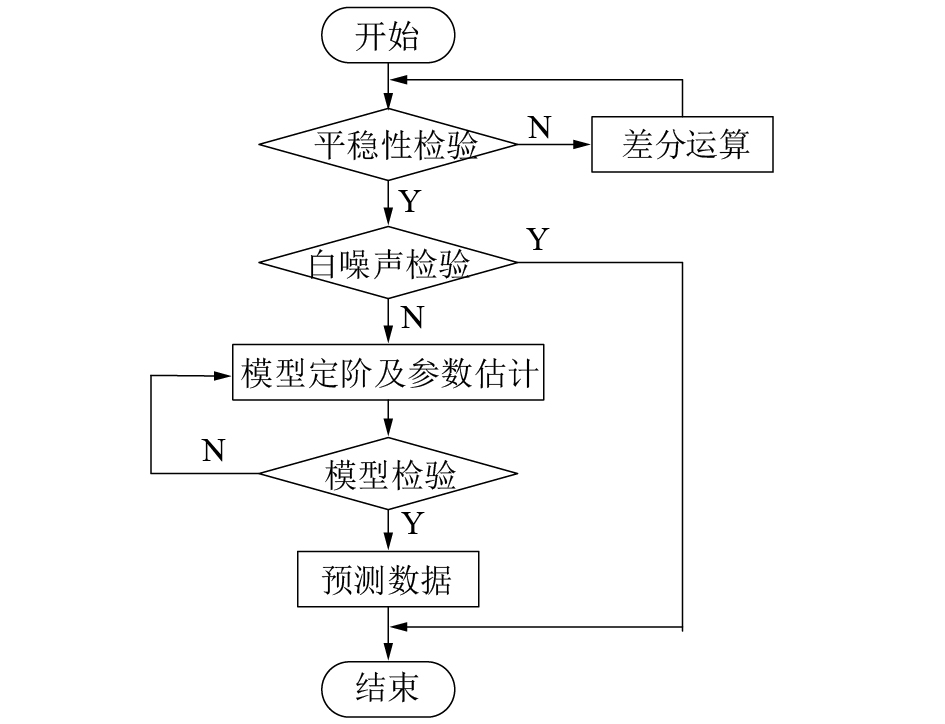
2 ARIMA模型的建立过程

ARIMA模型的建模过程如图1所示，模型定阶是建模最主要的部分^[10]。

2.1 数据预处理

以中国电力科学研究院特高压直流试验基地采集的宽频域电晕电流信号为建模分析对象，在R Studio环境下对其进行时间序列分析^[11]。图2为+800 kV输电等级下实测的电晕电流信号。由于测量设备采样率高，数据量大，本文选取其中一个周期的实测信号进行建模研究。

首先，对电晕电流信号进行单位根检验，判断信号平稳性。

$\begin{aligned}& \Delta {x_t} = \delta {x_{t - 1}} + \mathop \sum \limits_{i = 1}^m {\beta _i}\Delta {x_{t - i}} + {\varepsilon _t}\\& \Delta {x_t} = \alpha + \delta {x_{t - 1}} + \mathop \sum \limits_{i = 1}^m {\beta _i}\Delta {x_{t - i}} + {\varepsilon _t}\\& \Delta {x_t} = \alpha + \beta t + \delta {x_{t - 1}} + \mathop \sum \limits_{i = 1}^m {\beta _i}\Delta {x_{t - i}} + {\varepsilon _t}\end{aligned}$

原假设为H₀：δ=0，即序列 $X = \left\{ {{x_1},\;{x_2}, \cdots ,{x_t}} \right\}$ 是非平稳时间序列，备择假设为H₁：δ<0，即X是平稳时间序列^[12]。经检验，P值小于0.01，接受备择假设，即一周期的电晕电流信号无单位根，是一个平稳序列。

后对序列进行Ljung-Box白噪声检验，原假设为H₀：X是白噪声序列，备择假设为H₁：X非白噪声序列。经过检验，P值小于0.01，拒绝原假设。故实测电晕电流信号是平稳非白噪声信号。

2.2 模型识别

根据表1自相关系数(autocorrelation function，ACF)和偏自相关系数(partial autocorrelation function，PACF)规律对电晕电流信号进行模型定阶。

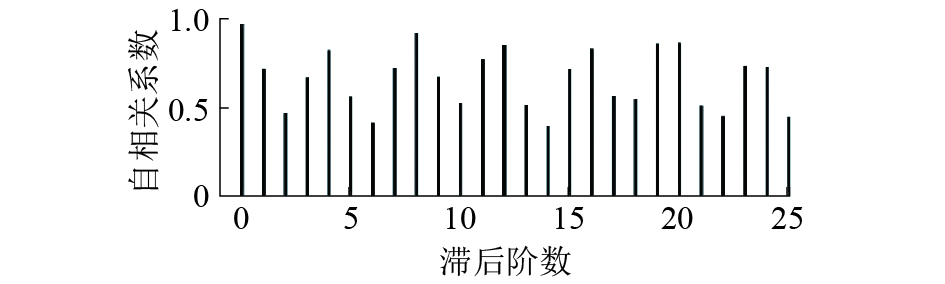
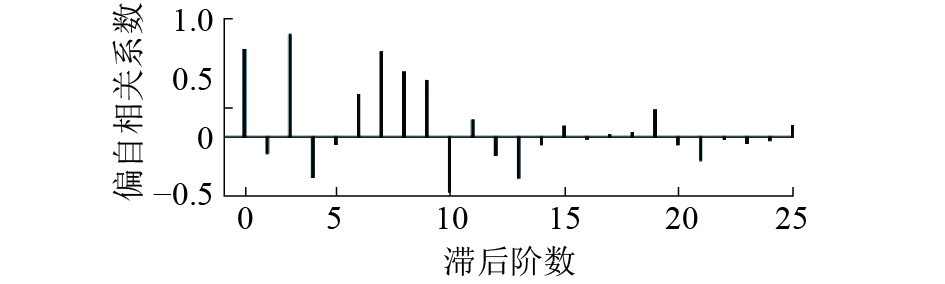
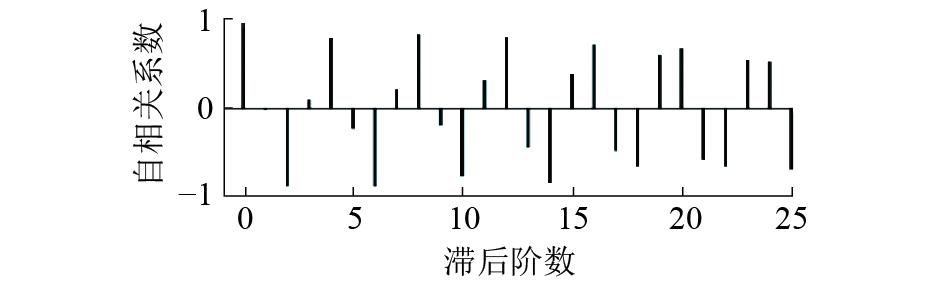
图3、4显示电晕电流序列延迟25阶的ACF和PACF，ACF和PACF均拖尾，且ACF始终有较大的峰值，PACF延迟13步后数值较小。本文对电晕电流序列进行一次差分，图5、6展示差分后电晕电流序列的ACF和PACF，ACF和PACF仍拖尾，PACF延迟13步后基本落入置信区间。有理由估计ARIMA(p, d, q)模型中p=13，d=0或1，q任取。

通过模型定阶，p、d、q系数不能唯一确定，本文对电晕电流信号建立多个ARIMA模型进行比较，将赤池信息准则(akaike information criterion，AIC)和贝叶斯信息准则(bayesian information criterion，BIC)作为选择标准。

$\begin{array}{l}{\rm{AIC}} = - 2{\rm{ln}} \; \mu + 2\sigma \\{\rm{BIC}} = - 2{\rm{ln}} \; \mu + \left( {{\rm{log}} \; N + 1} \right) \times \sigma \end{array}$

式中：μ为极大似然函数值，σ为模型中p、d、q系数个数，N为序列长度。AIC和BIC准则综合考虑模型拟合程度和系数个数两个方面。

本文建立的多个ARIMA模型的AIC、BIC函数如表2所示，选择AIC和BIC函数数值较小的模型。ARIMA(13, 0, 10)、ARIMA(13, 1, 5)、ARIMA(13, 1, 8)模型AIC、BIC值均较小，但ARIMA(13, 0, 10)模型p, q阶数过高，本文选择ARIMA(13, 1, 5)和ARIMA(13, 1, 8)模型进行下一步的研究。

2.3 参数估计及诊断检验

对上一步选择的ARIMA(13, 1, 5)和ARIMA(13, 1, 8)进行参数的显著性检验。经检验，2个模型的参数系数均为显著的非零项。

后对ARIMA(13, 1, 5)和ARIMA(13, 1, 8)进行模型的显著性检验，即对模型残差项进行Ljung-Box白噪声检验。ARIMA(13, 1, 8)模型检验P值小于0.01，而ARIMA(13, 1, 5)模型检验P值为0.71，故ARIMA(13, 1, 8)模型残差项不是白噪声，即序列有价值信息未提取完毕。ARIMA(13, 1, 5)模型为最终模型。ARIMA(13, 1, 5)拟合效果如图7所示。图中横坐标为时间序列点数，采样率为2.5 MHz，波形周期为0.02 s，故两时间序列点数之间间隔为4 μs。

ARIMA(13, 1, 5)模型系数如表3所示。

3 结果及分析

由于测量系统采样率高，一周期内信号数据长度较大，本文在ARIMA模型基础上采用了滚动ARIMA模型进行预测。用ARIMA(13, 1, 5)模型一次向前预测M个数据，预测完毕后，将当前M个数据更新为实际测量值，再滚动向后预测。

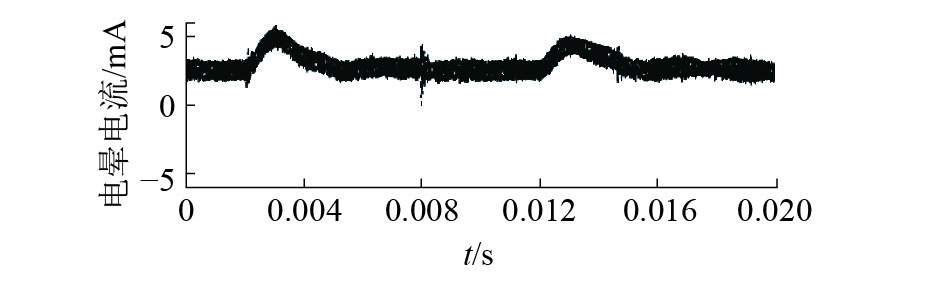
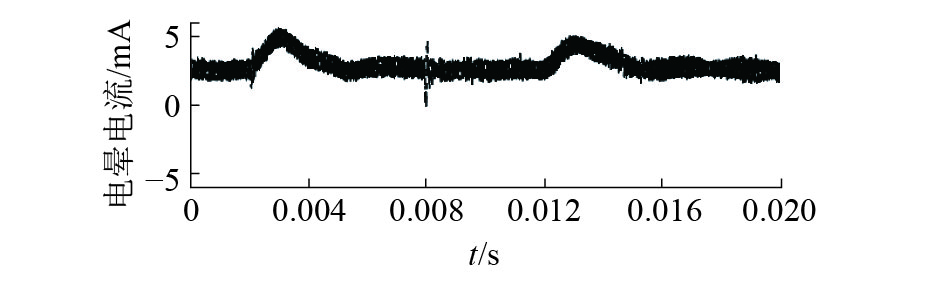
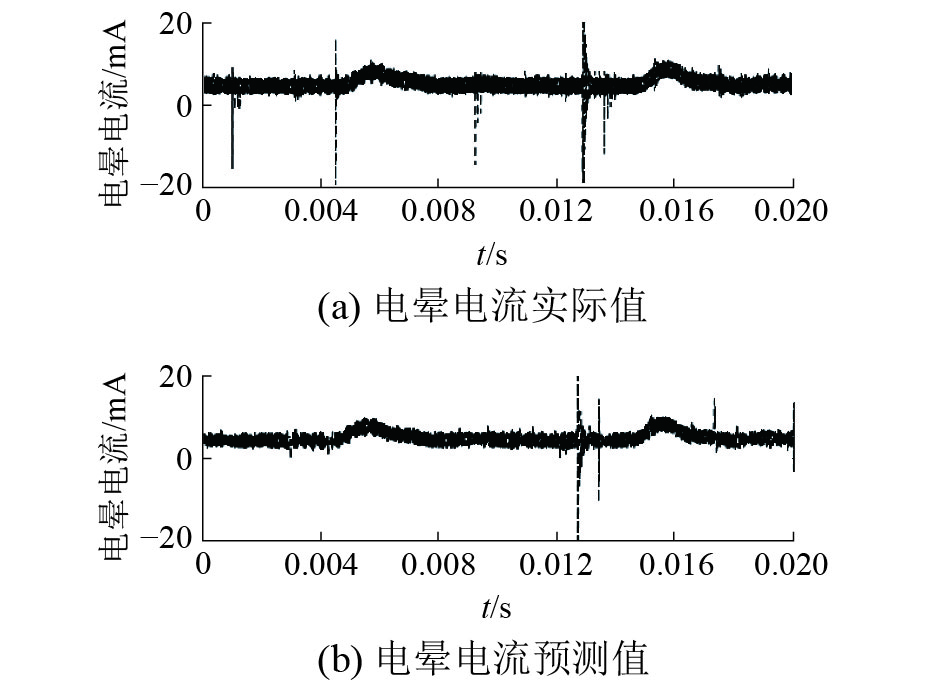
首先，对+800 kV输电等级下电晕电流建立ARIMA模型。图8为M=50，ARIMA(13, 1, 5)模型滚动1 000次预测结果，图9为M=100，ARIMA(13, 1, 5)模型滚动500次预测结果。如图10所示，对+1 000 kV输电等级下信号建立ARIMA(13, 1, 5)滚动模型。图10中预测值与实际值基本一致。

本文选用标准化后的平均绝对误差(normalized mean square error，NMSE)和均方误差(mean square error，MSE)作为模型预测效果的度量指标。

$\begin{aligned}& {\varepsilon _{{\rm{MSE}}}} = \frac{{\mathop \sum \nolimits_{i = 1}^N {{({y_i} - \hat{y_i})}^2}}}{N}\\& {\varepsilon _{{\rm{NMSE}}}} = \frac{{\mathop \sum \nolimits_{i = 1}^N {{({y_i} - \hat{y_i})}^2}}}{{\mathop \sum \nolimits_{i = 1}^N {{({y_i} - \hat{y_i} )}^2}}}\end{aligned}$

式中：N为预测样本个数，y_i为实际值， $\hat{y_i}$ 为预测值。MSE、NMSE值越小说明预测误差越小。

+800 kV输电等级下，模型预测度量结果如表4所示，对比分析可得，M=50ARIMA(13, 1, 5)滚动模型预测效果略优于M=100ARIMA(13, 1, 5)滚动模型，但总体效果相差不大。

8个时域指标^[13]，均方根x_rms、幅度平方根x_sra、峰度值x_kv、偏态值x_sv、峰峰值x_ppv、波峰因子x_cf、脉冲因子x_if和边际因子x_mf，用于描述电晕电流信号，其计算公式如下：

$\begin{aligned}& {x_{{\rm{rms}}}} = {(\frac{1}{N}\mathop \sum \limits_{i = 1}^N x_i^2)^{1/2}}\\& {x_{{\rm{sra}}}} = {(\frac{1}{N}\mathop \sum \limits_{i = 1}^N \sqrt {|{x_i}|} )^2}\\& {x_{{\rm{kv}}}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N {\left( {\frac{{{x_i} - \bar x}}{\sigma }} \right)^4}\\& {x_{{\rm{sv}}}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N {\left( {\frac{{{x_i} - \bar x}}{\sigma }} \right)^3}\\& {x_{{\rm{ppv}}}} = \max \left( {{x_i}} \right) - {\rm{min}}\left( {{x_i}} \right)\\& {x_{{\rm{cf}}}} = \frac{{\max \left( {|{x_i}|} \right)}}{{{{(\displaystyle\frac{1}{N}\mathop \sum \nolimits_{i = 1}^N x_i^2)}^{1/2}}}}\\& {x_{{\rm{if}}}} = \frac{{\max \left( {|{x_i}|} \right)}}{{\displaystyle\frac{1}{N}\mathop \sum \nolimits_{i = 1}^N \left| {{x_i}} \right|}}\\& {x_{{\rm{mf}}}} = \frac{{\max \left( {|{x_i}|} \right)}}{{{{(\displaystyle\frac{1}{N}\mathop \sum \nolimits_{i = 1}^N \sqrt {|{x_i}|} )}^2}}}\end{aligned}$

通过比较实测信号及模型预测信号时域指标是否接近，衡量模型预测效果。计算结果如表5所示，预测模型和实测电晕电流信号的时域统计指标相似，预测效果良好。

4 结论

1) 本文对特高压直流输电线路下的电晕电流进行时间序列分析，对+800 kV输电等级下信号建立ARIMA(13, 1, 5)模型。

2) 对+800 kV输电电压下的信号波形进行步长M=50及100的滚动预测。预测误差度量指标NMSE、MSE较小。同时设立8个时域统计指标，电晕实际波形与预测波形指标计算结果相似，预测效果良好。

3) 经建模计算表明，ARIMA(13, 1, 5)模型也同样适用于+1 000 kV输电等级下电晕电流信号的预测，本文所建模型具有较强的适用性。