我国北斗卫星导航系统已经日益完善,发展速度也逐步加快,关于北斗导航系统的各类问题尤其是在现有的北斗导航系统下提高北斗导航的定位精度更是需要大量的研究。伪距定位作为导航定位的基础,具有速度快、不存在整周模糊度、解算过程易于实现等特点。并且经过前人研究,北斗的伪距观测质量优于GPS,特别是北斗GEO卫星伪距观测量受多路径、硬件延迟及随机噪声的影响,比北斗其他卫星及GPS卫星都要小很多[1]。有效地提高伪距定位的精度不仅能利于单点定位,也能提高差分定位、相对定位的精度。因此提高伪距定位精度的研究是十分必要的。
载波相位平滑伪距是提高伪距观测值质量和定位精度的常用手段。优于相位观测量的精度远远高于伪距观测值得精度,根据组合和差分,可以利用载波相位历元间的差值来平滑伪距的观测值,达到提高伪距观测值精度的效果。传统Hatch滤波的优点是速度快,但是需要非常合理的选择平滑窗口的长度。针对于这点,文献[2]提出了一种分段滤波的方式,有效地抑制了电离层的误差累积,但是需要先验的数据分析。文献[3]提出了一种最优组合相位平滑算法,可以有效地提高定位精度,但是计算过程较为复杂,而且使用双频会带来模糊度的影响。文献[4]提出了一种基于扩展卡尔曼滤波的平滑算法,算法比Hatch滤波性能更好,但是前提需要准确地估计噪声模型,否则滤波很容易发散。文献[5]提出了一种自适应方差估计的滤波方式,能有效解决卡尔曼滤波的劣势,带来优良的滤波效果和定位精度。本文提出一种利用改进粒子群算法来优化Hatch滤波平滑窗口大小的方法,可以同样有效地提高滤波性能和定位精度。
1 载波相位平滑伪距的基本原理 1.1 基本原理导航的基本观测量有3种:伪距观测量、载波相位观测量、多普勒观测量[6]。在定位解算过程中常用的观测量是伪距观测两和载波相位观测量。伪距的观测方程为
| $\begin{aligned}& P_r^{^s}(t) = \sqrt {{{({X^{^{^s}}}(t) - {X_r})}^2} + {{({Y^{^{^s}}}(t) - {Y_r})}^2} + {{({Z^{^{^s}}}(t) - {Z_r})}^2}} + \\ & \quad \quad \quad {\delta _{{\text{ion}}}} + {\delta _{{\text{trop}}}} + {\delta _{{\text{tide}}}} + {\delta _{{\text{rel}}}} - c{\delta ^s}(t)\end{aligned} $ | (1) |
式中:
载波相位是指在接收时刻接受的卫星信号的相位相对于接收机产生的载波信号相位的测量值。载波相位观测量为
| $\begin{gathered} \lambda \phi _{{r}}^s({t_r}) = \rho _r^s({t_r},{t_s}) + c\delta ({t_s} - {t_r}) - {\delta _{ion}} + \hfill \\ \begin{array}{*{20}{c}} \quad {}&{}&{{\delta _{{\text{trop}}}}} \end{array} + {\delta _{{\text{tide}}}} + {\delta _{{\text{mul}}}} + {\delta _{{\text{rel}}}} + \lambda N_r^s + \varepsilon \hfill \\ \end{gathered} $ | (2) |
式中:
载波相位观测量是一个累积的载波相位观测结果[7]。通过电子器件对载波相位测量的精度优于波长的百分之一,达到毫米级,因此载波相位观测量的精度要远远高于伪距观测量精度[8]。但是高精度的载波相位定位解算必须要解算出正确的整周模糊度。而伪距定位中则不存在模糊度的求解问题,因而得到了广泛的应用。因此需要提出一种利用精确的载波相位值来平滑伪距观测值的方法,可以有效地结合两种观测值的优点并且提高伪距定位的定位精度。将伪距观测方程和载波相位观测方程简写为(以下均考虑对同一卫星而言的观测量)
| $P({t_n}) = R({t_n}) + I({t_n}) + {\varepsilon _P}({t_n})$ |
| $\lambda \phi ({t_n}) = R({t_n}) - I({t_n}) + {\varepsilon _\phi }{\text{(}}{t_n}{\text{) + }}\lambda {{N}}$ |
式中:
假设历元间没有发生周跳,整周模糊度N不发生跳变,相邻历元电离层延时变化
| $\begin{array}{l}P({t_n}) - P({t_n} - 1) = R({t_n}) - R({t_n} - 1) + {\varepsilon _P}({t_n}) - {\varepsilon _P}({t_n} - 1)\\\lambda \phi ({t_n}) - \lambda \phi ({t_n} - 1) = R({t_n}) - R({t_n} - 1) + {\varepsilon _\phi }{\rm{(}}{t_n}{\rm{)}} - {\varepsilon _\phi }{\rm{(}}{t_n} - 1{\rm{)}}\end{array}$ |
将相位差带入伪距差方程得
| $\begin{aligned} P({t_n}) - P({t_n} - 1) = & \lambda \phi ({t_n}) - \lambda \phi ({t_n} - 1) - \hfill \\& ({\varepsilon _\phi }{\text{(}}{t_n}{\text{)}} - {\varepsilon _\phi }{\text{(}}{t_n} - 1{\text{))}} + ({\varepsilon _P}({t_n}) - {\varepsilon _P}({t_n} - 1)) \hfill \\ \end{aligned} $ |
相邻历元间观测量的其它误差变化也比较小,因此可以认为
| $P({t_n}) - P({t_n} - 1) \approx \lambda \phi ({t_n}) - \lambda \phi ({t_n} - 1)$ | (3) |
设有n个历元观测值
| $\left\{ \begin{array}{l} \hat P({t_n}) = P({t_1}) + \lambda \phi ({t_n}) - \lambda \phi ({t_1}) \hfill \\ \hat P({t_n}) = P({t_2}) + \lambda \phi ({t_n}) - \lambda \phi ({t_2}) \hfill \\\quad \quad \quad \quad \quad \cdots \cdots \hfill \\ \hat P({t_n}) = P({t_n}) \hfill \\ \end{array} \right.$ |
将各式相加得
| $n\hat P({t_n}) = \sum\limits_{i = 1}^n {P({t_i})} + n\lambda \phi ({t_n}) - \lambda \sum\limits_{i = 1}^n {\phi ({t_i})} $ |
另
| $\hat P({t_n}) = \bar P(n) + \lambda \phi ({t_n}) - \frac{\lambda }{n}\sum\limits_{i = 1}^n {\phi ({t_i})} $ |
对相邻2个历元的观测相位平滑伪距值计算得到:
| $\hat P({t_n}) = P({t_n} - 1) + \lambda \phi ({t_n}) - \lambda \phi ({t_n} - 1)$ |
Hatch滤波的本质是利用算术平均运算提取出码伪距的低频成分,利用时间差分算子提取相位的高频成分,以此来提高伪距观测量的精度。Hatch滤波常用分析模型为[11]
| $\hat P({t_n}) = \frac{1}{M}P({t_n}) + \frac{{M - 1}}{M}\left[ {\hat P({t_{n - 1}}) + \lambda \phi ({t_n}) - \lambda \phi ({t_{n - 1}})} \right]$ |
式中M为Hatch滤波器的长度,M的值取决于观测采样间隔
假设伪距观测值与相位观测值不相关,不同历元同一类型的观测量之间也不相关,各历元的伪距观测值精度相同,相位观测值精度也相同,则设伪距观测量的误差标准差为
| ${\sigma _{\hat P}}^2 = \frac{1}{n}{\sigma _P}^2 + \frac{{(n + 1)}}{n}{\sigma _\phi }^2$ |
又由于
| ${\sigma _{\hat P}} = \frac{{{\sigma _P}}}{{\sqrt n }}$ | (4) |
由式(4)可知,载波相位平滑伪距的测量精度比原伪距观测量的测量精度提高了
Hatch滤波方法如果针对双频无电离层组合观测量进行平滑处理,精度很高,而且相位平滑伪距一定的次数后,平滑伪距的精度可以与相位无电离层组合相位观测值的精度相当[13],但是组合值会带来模糊度的问题,增加了定位解算的复杂度;如果针对于单频伪距,则会引起电离层误差的累积,因此Hatch滤波必须要合理选择平滑时间窗口,才能避免电离层的影响并达到良好的滤波效果。
2 改进粒子群(IPSO)算法描述假设在待解决问题中解是
粒子群算法的基本流程如下[14]:
1)对种群规模M进行初始化,初始值设为
2)设
3)计算每个粒子的
| ${P_i}(t) = \arg \min \{ f({P_i}(t)),f({ X_i}(t))\} $ |
4)依次对每个粒子对应位置
| $G(t) = \arg \min \{ f({P_1}(t)), \cdot \cdot \cdot ,f({P_i}(t)), \cdot \cdot \cdot ,f({P_M}(t))\} $ |
5)判断是否满足迭代的终止条件(最大迭代次数),如果满足,则
针对不同问题粒子群的优化方式各不同。通过分析本章需要优化的问题,采用了文献[15]中作者提出的基于种群分类与动态学习因子的改进粒子群算法,该算法改进了粒子更新速度的方式,使粒子在寻优的过程中能更快更有效地收敛到最优解,该算法的基本流程如下:
1)初始化粒子群种群规模,迭代次数,随机产生粒子的初始种群以及每个粒子的初速度。
2)初始化学习因子
| $\left\{ \begin{array}{l} C = 5 \hfill \\ {C_1} = 2/(1 + {t^{1/4}}) \hfill \\ {C_2} = t/{t_{\max }} \hfill \\ \end{array} \right.$ |
式中:
3)初始第
4)利用改进后的粒子速度更新方式更新每个粒子的值和速度,改进后的粒子更新方法如式(5)、(6)所示。
如果
| $ { V_i}(t) = \left\{ \begin{array}{l}w{ V_i}(t - 1) + C{\rm{rand}}()({P_i}(t - 1) - { X_i}(t - 1)),\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, f({ X_i}(t - 1)) - \mu < - E({f^2})\\w{ V_i}(t - 1) + C{\rm{rand}}()(G(t - 1) - { X_i}(t - 1)),\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, f({ X_i}(t - 1)) - \mu < E({f^2})\\w{ V_i}(t - 1) + {C_1}{\rm{rand}}()({P_i}(t - 1) - { X_i}(t - 1)){\rm{ + }}{C_2}{\rm{rand}}()(G(t - 1) - { X_i}(t - 1)),\quad |f({ X_i}(t - 1)) - \mu | < E({f^2})\end{array} \right. $ | (5) |
否则:
| $ { V_i}(t) = \left\{ \begin{gathered} {V_{\max }}\begin{array}{*{20}{c}} {}&{{ V_i}(t) > {V_{\max }}} \end{array} \hfill \\ - {V_{\max }}\begin{array}{*{20}{c}} {}&{{ V_i}(t) < - {V_{\max }}} \end{array} \hfill \\ \end{gathered} \right.$ | (6) |
更新权值
5)通过对所有粒子循环确定第
这种改进方式可以让粒子自适应地选择贴近社会模型或者认识模型,有效地增大了粒子寻求最优解的概率,提高了粒子群算法的搜索性能,并且能更高效地收敛到最优解。
3 IPSO-HATCH算法描述Hatch滤波中平滑因子M直接决定了滤波的效果的优劣程度,如果M选择合理,则应该满足N个历元的滤波输出和原测量值的均方值最小,因此利用IPSO对M进行寻优的适应度函数可以选择为[16]
| $f = \frac{1}{N}\sum\limits_{i = 1}^N {(\hat P(i) - P(i))} $ |
式中
1)历元
2)为了减小粒子群算法的搜索范围和计算复杂度,当
3)
4)将
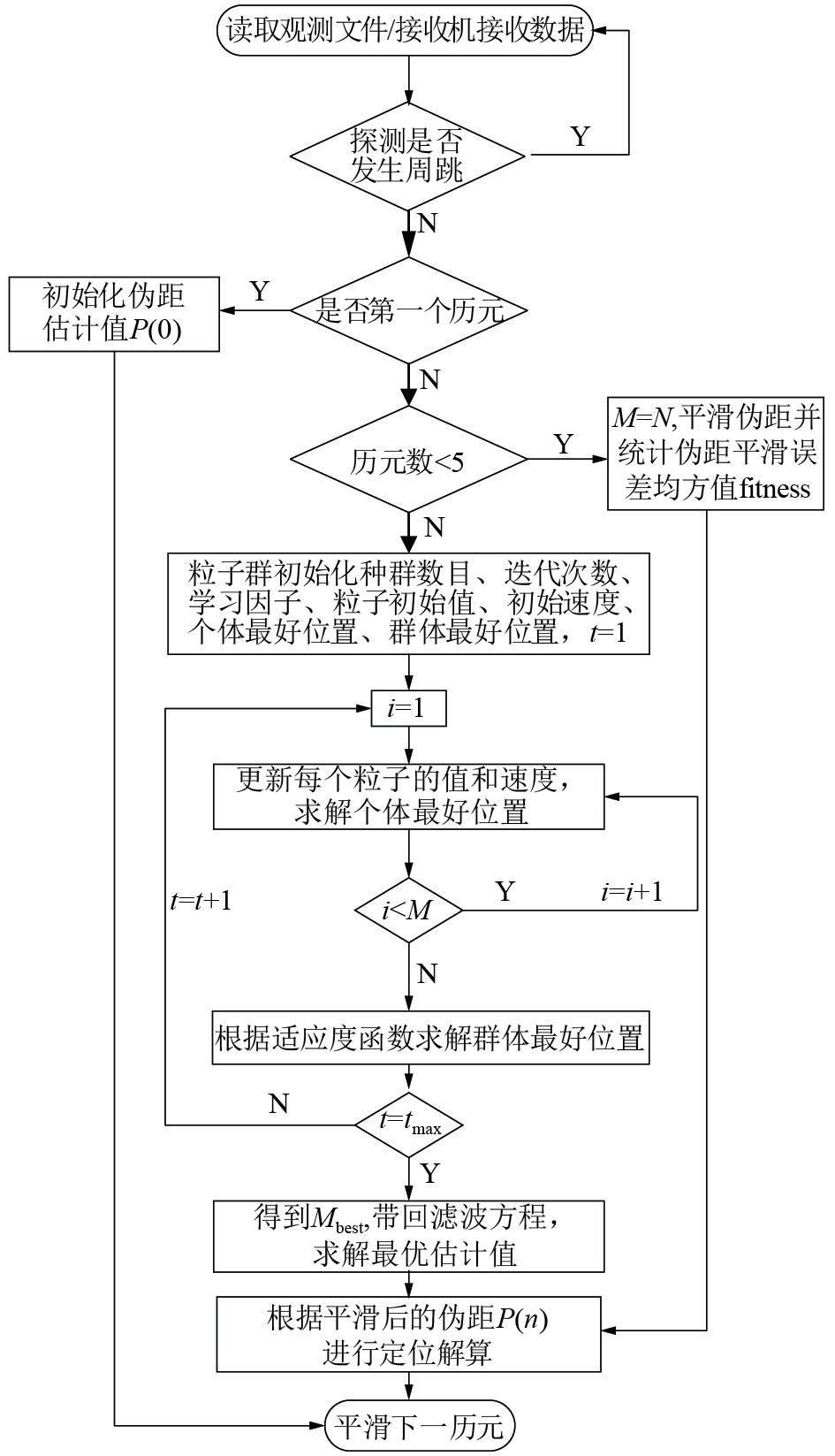
利用IPSO-HATCH算法进行相位平滑伪距定位的总体流程图如图1所示。
|
Download:
|
| 图 1 IPSO-HATCH算法相位平滑伪距定位流程 | |
实验程序开发环境为
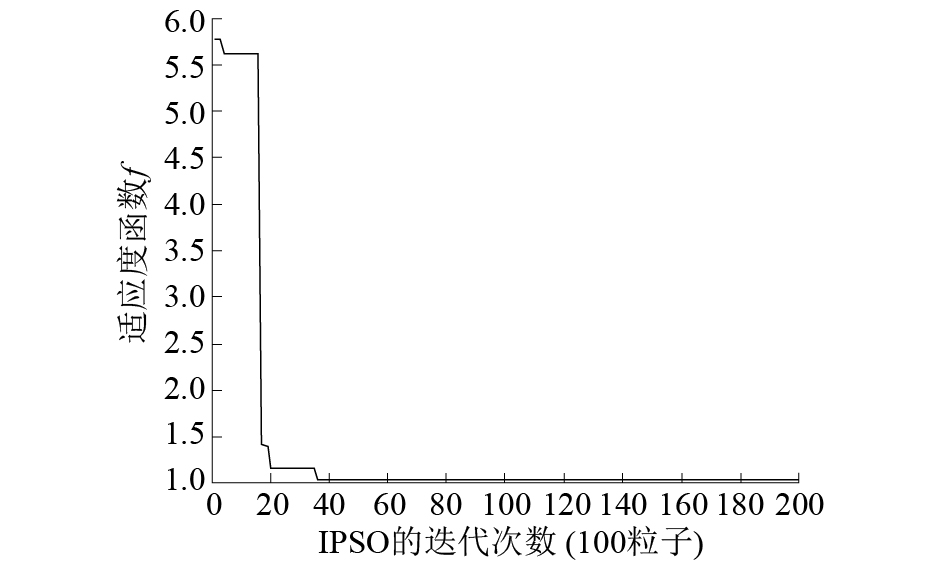
通过反复试验,对某一收敛速度较慢的历元中选取100粒子迭代200次来统计IPSO的收敛速度,其收敛效果如图2所示。
|
Download:
|
| 图 2 粒子群算法收敛速度 | |
由图2可见在收敛较慢的历元里,IPSO仍然可以保证在在迭代次数40次以内收敛达到最优值,并且通过大量试验,很多历元的收敛迭代次数在5次以内。因此可以表明对于本章问题的适应度函数,此种方法可以快速地收敛到最优值,根据适应度函数
本章实验分别选取未平滑伪距、普通Hatch滤波平滑伪距、IPSO-HATCH滤波平滑伪距进行对比实验来验证算法的有效性,采用双频接收机和精密星历进行精密定位的值作为近似真实坐标进行比较,坐标系为CGCS2000。3种定位结果的X、Y、Z轴的误差如图3~5所示。

|
Download:
|
| 图 3 未平滑伪距定位X、Y、Z坐标误差 | |
|
Download:
|
| 图 4 Hatch滤波平滑伪距定位X、Y、Z坐标误差 | |

|
Download:
|
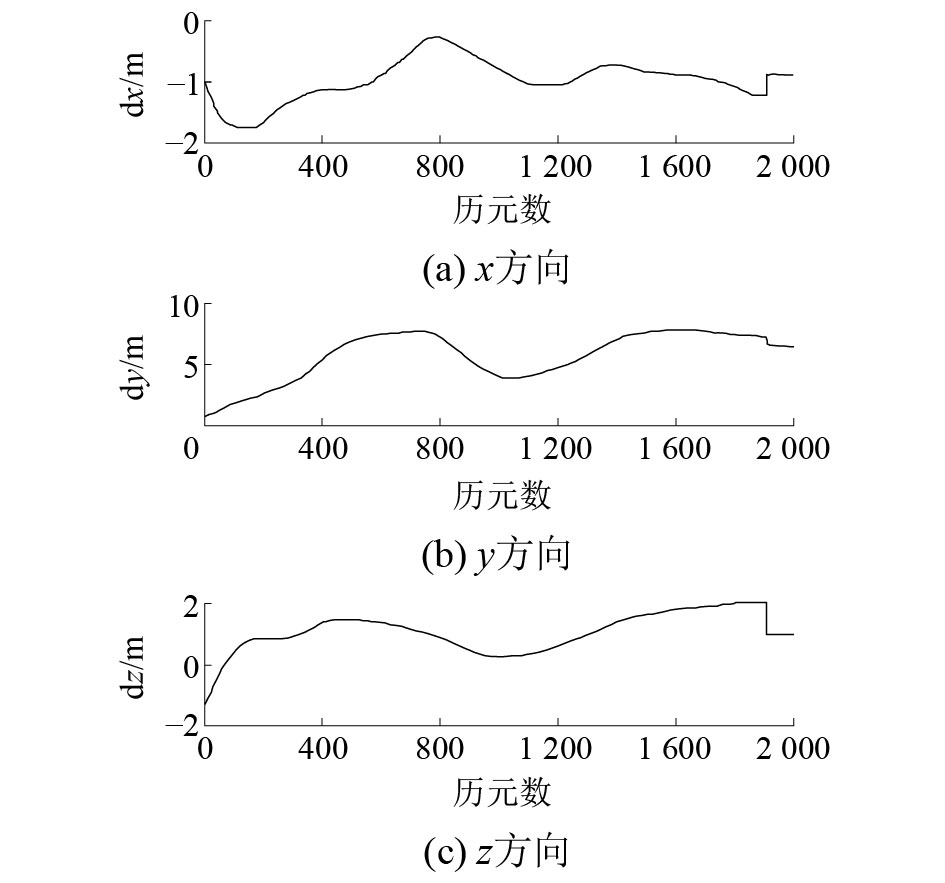
| 图 5 IPSO-HATCH平滑伪距定位X、Y、Z坐标误差 | |
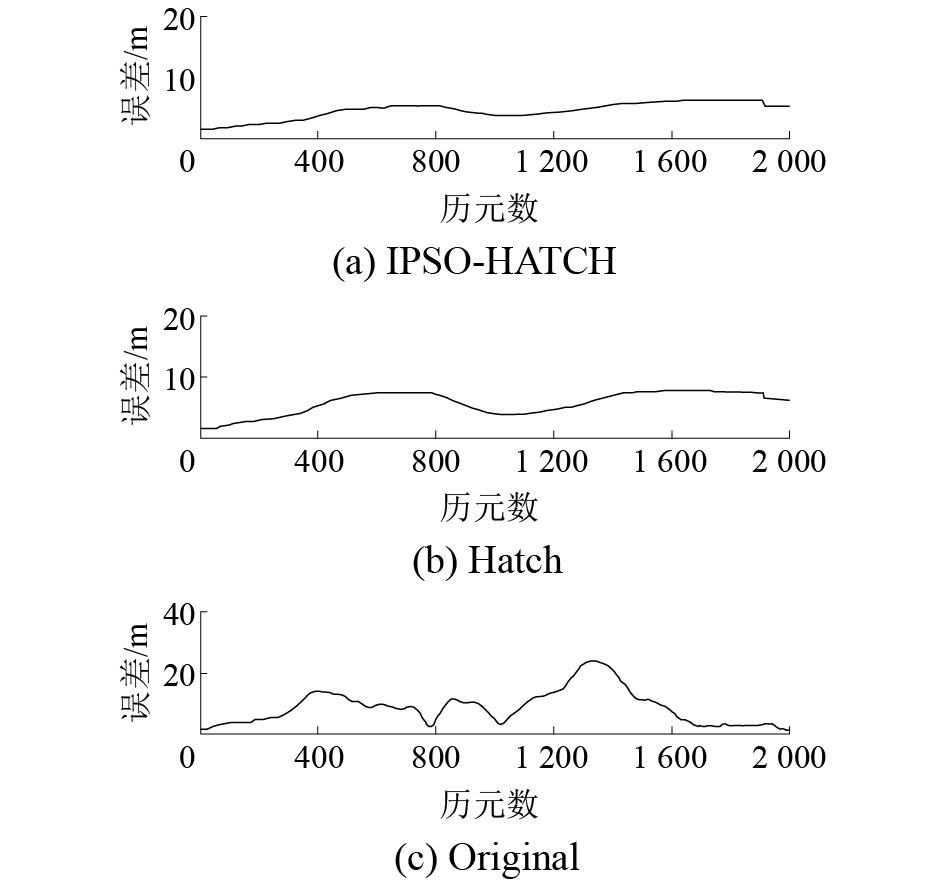
3种定位结果相对于真实值的三维几何距离偏差如图6所示。
|
Download:
|
| 图 6 三维坐标几何距离误差对比 | |
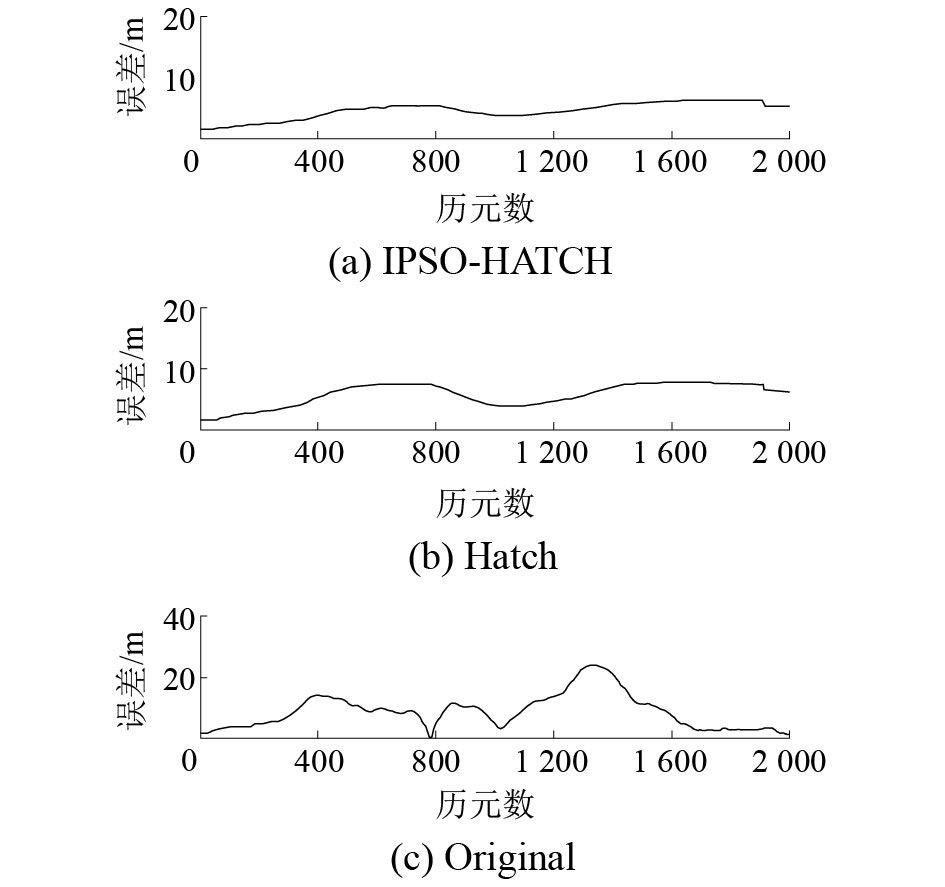
3种定位结果相对于真实值的二维XY几何距离偏差如图7所示。
|
Download:
|
| 图 7 X、Y二维坐标几何距离误差对比 | |
由图3~7可以看出:1)Hatch滤波和IPSO-HATCH滤波与未平滑的伪距定位结果对比,在精度上都有了很大提升,而且解算结果的稳定度相对也有一定的提高;2)IPSO-HATCH算法对比于传统的Hatch算法,在精度上也有一定的提高,并且在解算结果上也更加平滑稳定,在X轴和Z轴的精度可以控制在2 m以内,在Y轴的精度也可控制在5 m以内;3)在三维坐标几何距离偏差和X、Y二维几何距离偏差中,IPSO-HATCH算法在3种解算算法中精度最高,结果最稳定,精度可以控制在10 m以内,甚至在多数情况下可以在5 m以内。
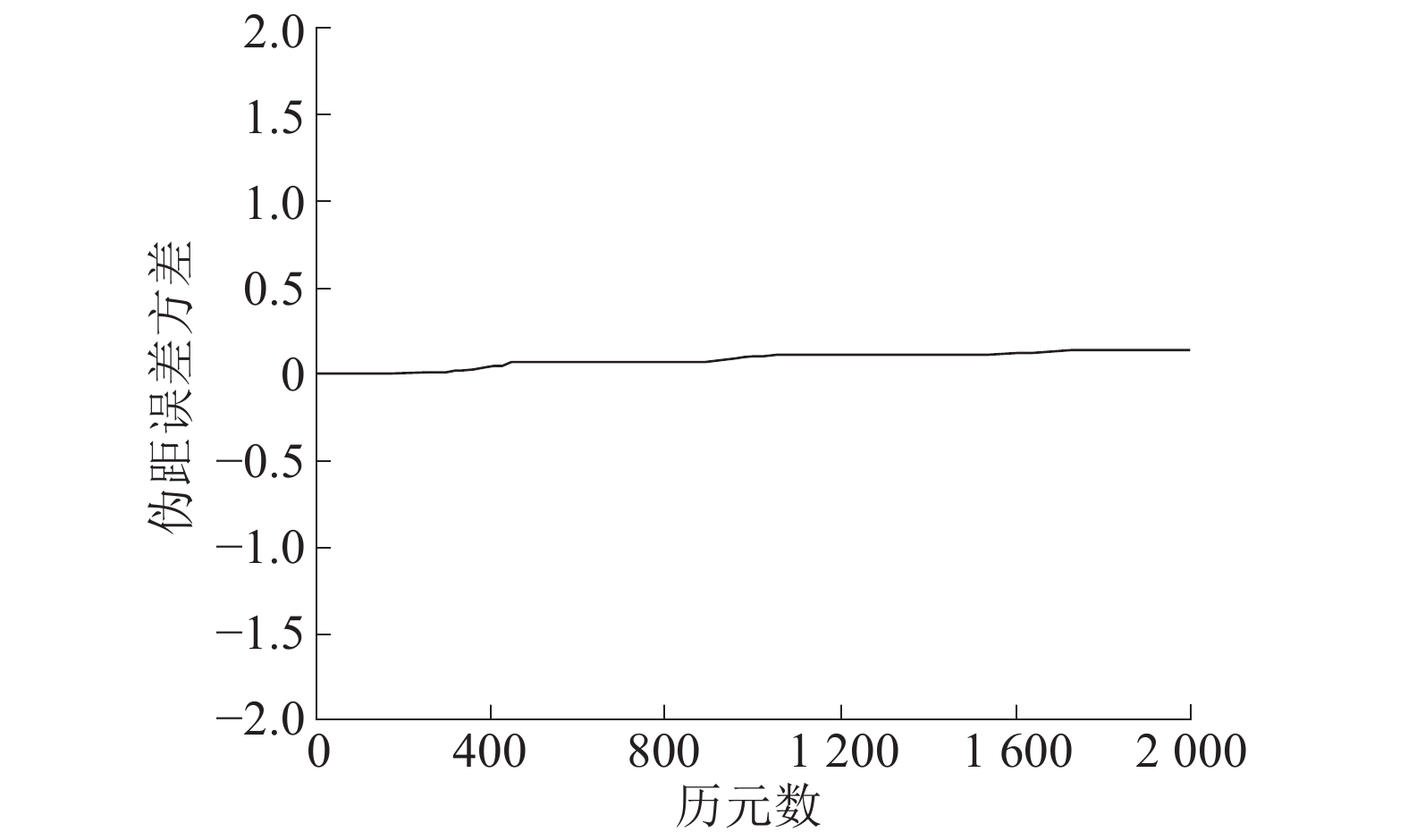
4.2.2 独立实验分析实验中对每一个卫星的伪距测量值都进行了平滑处理,选取C01的卫星进行分析,则C01卫星平滑后伪距的误差方差如图8所示。
|
Download:
|
| 图 8 C01卫星伪距误差方差 | |
由图8可以看出,平滑后的伪距误差方差比较稳定,并且方差较小,证明了平滑后的伪距观测值更加精确,有效地减小了误差。
针对于定位结果,采取RMS值来分析三维坐标X、Y、Z值的精确稳定程度,如图9所示。

|
Download:
|
| 图 9 IPSO-HATCH算法三维坐标RMS值 | |
由图9可以看出,X、Y、Z三坐标的解算结果都十分稳定,Y轴的解算精度略低,并且在最后出现了较小幅的变化,X和Z轴的解算坐标RMS值基本稳定。
5 结束语本文通过分析以往载波相位平滑伪距算法的优缺点,结合改进粒子群算法的高效的寻优性能,提出了一种IPSO-HATCH结合的平滑滤波算法,利用IPSO自适应的选择最优的Hatch滤波平滑窗口,既保留了Hatch滤波的快速、容易实现的特点,又让滤波的结果更加稳定可靠。
| [1] |
严丽, 黄丁发, 冯威, 等. COMPASS与GPS伪距单点定位性能比较研究[C]//第三届中国卫星导航学术年会电子文集——S06北斗/GNSS测试评估技术. 广州: 中国卫星导航系统管理办公室, 2012.
( 0) 0)
|
| [2] |
邹波, 高飞. 基于改进的Hatch滤波GPS/BD组合系统单点定位[J]. 城市勘测, 2014(5): 26-29. ( 0) 0)
|
| [3] |
郭建锋, 欧吉坤, 袁运斌, 等. 双频GPS数据的最优相位平滑伪距算法研究[J]. 自然科学进展, 2008, 18(2): 221-224. ( 0) 0)
|
| [4] |
杨春燕, 吴德伟, 卢艳娥, 等. 基于补充卡尔曼滤波的载波相位平滑伪距算法[J]. 空军工程大学学报: 自然科学版, 2008, 9(5): 52-56. ( 0) 0)
|
| [5] |
LEE J Y, KIM H S, CHOI K H, et al. Adaptive position-domain carrier-smoothed code filter based on innovation sequences[J]. IET radar, sonar & navigation, 2014, 8(4): 336-343. ( 0) 0)
|
| [6] |
周动力. 基于LAMBDA法的模糊度解算方法比较分析[D]. 青岛: 山东科技大学, 2008.
( 0) 0)
|
| [7] |
XU Guochang. GPS理论、算法与应用[M]. 李波, 罗海英, 北京跟踪与通信技术研究所, 等译. 北京: 清华大学出版社, 2011.
( 0) 0)
|
| [8] |
HOFMANN-WELLENHOF B, LICHTENEGGER H, WASLE E. 全球卫星导航系统: GPS, GLONASS, Galileo及其他系统[M]. 程鹏飞, 蔡艳辉, 文汉江, 等译. 北京: 测绘出版社, 2009.
( 0) 0)
|
| [9] |
戴连君, 唐涛, 蔡伯根, 等. 基于北斗卫星载波相位平滑伪距的列车定位方法[J]. 铁道学报, 2012, 34(8): 64-69. ( 0) 0)
|
| [10] |
刘广军, 郭晶, 罗海英. GNSS最优载波相位平滑伪距研究[J]. 飞行器测控学报, 2015, 34(2): 161-167. ( 0) 0)
|
| [11] |
李晨阳. 载波相位在提高GNSS接收机精度中的应用研究[D]. 北京: 北京邮电大学, 2013.
( 0) 0)
|
| [12] |
刘瑞华, 杨兆宁, 詹先龙. 北斗系统载波相位平滑伪距研究[J]. 中国民航大学学报, 2012, 30(3): 28-31. ( 0) 0)
|
| [13] |
常志巧, 胡小工, 郭睿, 等. CNMC与Hatch滤波方法比较及其在北斗相对定位中的精度分析[J]. 中国科学: 物理学 力学 天文学, 2015, 45(7): 079508. ( 0) 0)
|
| [14] |
张建科, 王晓智, 刘三阳, 等. 求解非线性方程及方程组的粒子群算法[J]. 计算机工程与应用, 2006, 42(7): 56-58. ( 0) 0)
|
| [15] |
毕晓君. 信息智能处理技术[M]. 北京: 电子工业出版社, 2010.
( 0) 0)
|
| [16] |
张旭辉, 林海军, 刘明珠, 等. 基于蚁群粒子群优化的卡尔曼滤波算法模型参数辨识[J]. 电力系统自动化, 2014, 38(4): 44-50. DOI:10.7500/AEPS20130331006 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


