若不考虑传统主观经验诊断、直接性能测试等方法，近年来，液压泵故障诊断方法大致包括三大类：基于模型解析、基于信号处理和基于人工智能的故障诊断方法。基于模型解析的方法包括参数估计法、状态估计法等。基于信号处理的方法包括时域、频域、时频分析等，小波包分析是其典型代表^[1]，基于信号处理的方法一般直接提取信号时频域的各种信号参数，诸如方差、各频带或频点幅值等，通过与液压泵正常工作状态下的这些参数进行比较，或者在分析液压泵工作机理的基础上，推导出故障在这些参数中的表现形式，从而实现液压泵故障诊断。基于人工智能的液压泵故障诊断方法包括专家系统、D-S证据推理、故障树、灰色理论、神经网络、支持向量机(support vector machines, SVM)等^[2-3]。

信号处理方法、人工智能方法和其他领域方法相互融合进行故障诊断是目前该领域的研究热点^[4-13]。考虑到遗传算法的全局寻优能力、SVM对样本数量要求少但其参数选择具有随机性以及小波包频带能量和时域统计量组成的特征向量具有稳定性，本文将GA-SVM和小波包分解应于液压泵的故障诊断中。利用液压泵故障样本和正常样本验证了方法的有效性，以及通过与网格搜索法对比验证了方法的性能。

1 液压泵故障诊断方法

本文提出的液压泵故障诊断方法包括传感器信号特征提取、支持向量机参数寻优算法(genetic algorithm based support vector machines，GA-SVM)对SVM参数进行优化、SVM训练和最终的SVM故障分类。

信号特征提取主要内容是对固定长度的信号进行小波包分解重构等运算，从而得到小波包频带能量，这些信号可以是液压泵出口压力、出口流量、转速或者振动信号等等，本文主要针对液压泵出口流量。小波包频带能量与均方根值和方差这两个时域统计量组合而成得到的特征向量用来表征信号的特性。

GA-SVM过程简要地说就是将一批做好标签的样本输入到算法中，算法迭代进行SVM交叉验证，并且保存最优，从而得到SVM最优参数即惩罚因子和径向基核函数(radial basis function，RBF)的参数。SVM训练就是在该参数下训练SVM而得到可用于诊断的SVM模型。

SVM故障分类也即诊断就是将从信号中提取的特征向量输入到训练好的SVM中，进行故障分类。

2 信号特征提取

如上文所述，信号特征为小波包频带能量和时域统计量的组合。特征提取过程如下：

1)利用小波包分解将信号分解和重构。本文利用db5小波包对信号进行2层分解得到4个频段的小波包系数[u₃₁ u₃₂ u₃₃ u₃₄]，其中 ${u_{3i}}$ ( $i = 1,2,3,4$ )的长度为原信号长度的1/4。

然后根据小波包系数和小波包函数，对信号在各小波包频带进行信号重构，得到与原始信号长度一致的各频带信号[U₃₁ U₃₂ U₃₃ U₃₄]。

2)将重构所得各小波包频带信号按照

${E_{3i}} = \mathop \sum \limits_{j = 1}^N {\left| {{U_{3ij}}} \right|^2}$

求均方值也即模值，式中N为原始信号长度，得到各小波包频带信号的能量[E₃₁ E₃₂ E₃₃ E₃₄]，即所谓的小波包频带能量。

将其按式(1)归一化

$\bar {\,\,{{{E}}_{3i}}} = \frac{{{E_{3i}}}}{{\mathop \sum \nolimits_{i = 1}^4 {E_{3i}}}}$

(2)

从而得到

$\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\bar {\,\,\,{E_{31}}} }&{\bar {\,\,\,{E_{32}}} } \end{array}}&{\begin{array}{*{20}{c}} {\bar {\,\,\,{E_{33}}} }&{\bar {\,\,\,{E_{34}}} } \end{array}} \end{array}} \right]$

3)对原始信号x按式(2)、(3)分别求统计量方差和均方根值，它们分别代表了原始信号的波动程度和能量总体水平。

${s^2} = \frac{1}{N}\mathop \sum \limits_j^N {\left( {{x_j} - \bar x} \right)^2}$

(3)

${{\rm{x}}_{{\rm{rms}}}} = \frac{1}{N}\mathop \sum \limits_j^N {\left( {{x_j}} \right)^2}$

(4)

4)将小波包频带能量、统计量反差和均方根值组合得到特征向量T：

${T} = \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{{\bar E}_{{\rm{31}}}}}&{{{\bar E}_{{\rm{32}}}}}&{{{\bar E}_{{\rm{33}}}}}\end{array}}&{\begin{array}{*{20}{c}}{{{\bar E}_{{\rm{34}}}}}&{{s^2}}&{{x_{{\rm{rms}}}}}\end{array}}\end{array}} \right]$

3 GA-SVM算法

GA-SVM即遗传算法优化的支持向量机，主体思想是应用实值编码遗传算法优化SVM的惩罚因子和核函数参数的选择。

3.1 支持向量机原理

支持向量机是由最大间隔线性分类器发展而来的，主要思想是根据结构风险最小化原则，通过求解二次规划，寻找最佳分类超平面，使正样本和负样本之间的间距最大，从而使得样本被误分的可能性尽可能降低。

首先考虑简单情况，即样本只存在2种类别且为线性可分，这种情况下的分类超平面为

$\varphi \left( x \right) = \omega x + b = 0$

(6)

式中： $\omega $ 为分类超平面的法向量，b为常数。对任给样本x将其带入式(4)有

$\varphi \left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\omega x + b > 0,x \in {\Omega _ + }} \\ {\omega x + b < 0,x \in {\Omega _ - }} \end{array}} \right.$

式中： ${\Omega _ + }$ 表示正样本集， ${\Omega _ - }$ 表示负样本集。

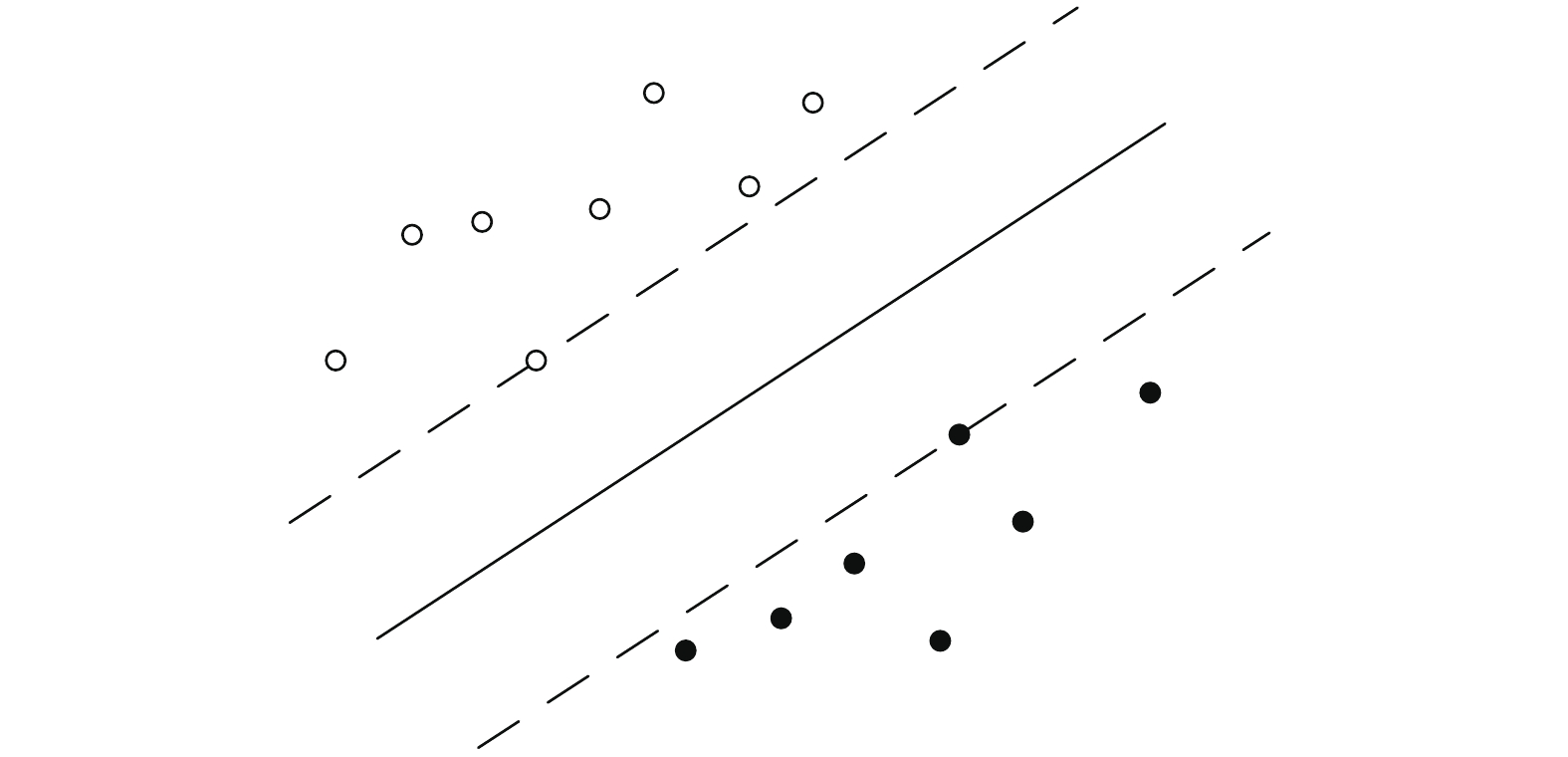
如图1所示，空心的圈代表正类样本，实心的圈代表负样本，中间实线代表分类超平面 $\varphi \left( x \right) = 0$ ，位于两类样本边缘且与分类超平面欧式距离都为 $\gamma $ 的2个点分别设为 ${x_0}$ 与 ${x_1}$ ，过这2个点作平行于 $\varphi \left( x \right) = 0$ 的超平面分别为

$\left\{ \begin{array}{l}{H_0}:\varphi \left( x \right) = \gamma \\{H_1}:\varphi \left( x \right) = - \gamma \end{array} \right.$

方程中可以通过调整 $\omega $ 和b的模，使得等式右边的 $\gamma = 1$ ，此时将 ${x_0}$ 与 ${x_1}$ 之间的欧式距离定义为两类样本之间的距离，则该距离为 $2/\omega $ 。SVM训练的目的就是根据训练样本找到使该距离最大的 $\omega $ 和 $b$ ，另外此处的边缘点 ${x_0}$ 、 ${x_1}$ 即所谓的支持向量，它们不唯一。

针对样本不是线性可分的情况，根据VC维理论，SVM引入核函数将样本映射到高维空间，使样本线性可分。例如本文选用的RBF核函数，只要核函数参数 $g$ 选取得当，原本线性不可分的样本经过RBF核函数映射之后变得线性可分。

同时考虑到即使在高维空间样本线性可分，但是可能存在某些支持向量即边缘点之间的间隔过小的情况，SVM引入软间隔机制，即在训练时不考虑一些间隔过小的点。

以上的措施虽然使得非线性可分情况可以用线性分类器进行分类，但是也需要人为设定不同类别的核函数及其参数和软间隔的惩罚因子。但是针对这些参数的设定目前还没有具体的指导方法，一般都是通过网格选取法或者其他各种寻优方法进行参数的选择。对于多分类问题，例如对 $k$ 分类问题，有很多解决策略，常用方法有一对一法，即为任意两类样本之间设计一个基本二分类SVM，得到 $k\left( {k - 1} \right)/2$ 个上述的基本二分类SVM，对样本进行分类时，样本同时输入到所有的二分类SVM中进行分类，这些二分类SVM得到的结果看成是它们为样本属于哪种类别进行投票，票数最多的类别即为分类结果，所以多分类SVM的基础还是基本二分类SVM。

本文SVM选用的核函数为径向基核函数(radial basis function，RBF)，所以本文实际需要设定的SVM参数为惩罚因子 $c$ 和RBF的模型参数 $g$ 。

3.2 遗传算法

遗传算法是一种借鉴进化论思想即生物进行过程提出的演化算法，主要通过对种群进行适应度计算，从而根据适应度进行基因的选择、遗传、变异等隐含并行性的操作，在搜索过程中种群基因能够获取和积累有关搜索空间的知识，经过一定迭代次数后解码基因即可得到问题最优解或近似最优解，这种特性为非线性甚至于不存在明确表达式问题的寻找最优解带来了一种简单可行的方法。尤其是遗传算法种群中每个个体的适应度计算可以并列进行的优点，使其非常适合于某些较为复杂且耗时的寻优问题。

遗传算法作为一种随机算法，其时间复杂度虽然目前暂无明确的分析方法，但是根据Holland教授提出的模式定理和堆积木假设^[14]，具有低模阶、短模长和高适应度特性的模式，其数目将在群体后代基因中呈指数增长，以及不同模式可以像堆积木一样被遗传算子拼接在一起组合成具有更高适应度的基因。对于不存在遗传算法欺骗问题的情况，遗传算法能够较快地收敛到最优点附近。因此，理论上遗传算法相较于网格搜索法这类穷举型参数寻优方法具有明显的速度优势。需要说明的是，虽然本文采用的实值编码遗传算法与基本二进制编码的遗传算法有一定的区别，但是已经有专家学者研究并且得出这类编码格式的遗传算法也满足模式定理的结论^[15]。

3.3 基于实值编码遗传算法的支持向量机参数优化

本文所述的SVM参数优化过程即使用实值编码的遗传算法进行支持向量机参数的寻优。

主要思想是先确定SVM的惩罚因子和RBF模型参数的寻优范围，然后使用实值编码遗传算法进行参数寻优，找到最优参数后，使用该参数训练SVM模型，模型训练好后即可用于对实际测量所得的数据进行故障分类。

算法流程如图2所示，算法中具体参数设置和细节如下所述：

1)遗传算法的参数寻优空间为 $c \in \left[ {{2^{ - 10}},{2^{10}}} \right]$ ， $g \in \left[ {{2^{ - 10}},{2^{10}}} \right]$ 。

2)遗传算法的种群基因即 $c$ 和 $g$ 两个实数。实值遗传算法对基因进行编辑的操作算子具体实现如下：

a)选择算子为用适应度最高个体的基因替换最差个体的基因，同时保留最优个体到全局最优个体；

b)变异算子是将基因 $c$ 和 $g$ 分别与能保证它们不超出寻优空间的随机实数r相加，即

$c = \left\{ {\begin{array}{*{20}{c}} {c' + r,c' + r < {2^{10}}} \\ {{2^{10}},c' + r \geqslant {2^{10}}} \end{array}} \right.$

c)交叉算子首先在种群中随机选择2个个体，假设第1个个体的基因为 ${c_1}^\prime $ 和 ${g_1}^\prime $ ，第2个个体的基因为 ${c_2}^\prime $ 和 ${g_2}^\prime $ ，分别产生2个随机实数 ${w_c} \in \left( {0,1} \right)$ 和 ${w_g} \in \left( {0,1} \right)$ ，然后按照式(5)分别产生2个新一代个体的基因 ${c_1}$ 、 ${g_1}$ 和 ${c_2}$ 、 ${g_2}$ ，也即新一代个体。

$\left\{ \begin{gathered} {c_1} = {w_c}{c_1}^\prime + \left( {1 - {w_c}} \right){c_2}^\prime \\ {g_1} = {w_g}{g_1}^\prime + \left( {1 - {w_g}} \right){g_2}^\prime \\ {c_2} = \left( {1 - {w_c}} \right){c_1}^\prime + {w_c}{c_2}^\prime \\ {g_2} = \left( {1 - {w_g}} \right){g_1}^\prime + {w_g}{g_2}^\prime \\ \end{gathered} \right.$

(10)

4 实验结果与分析

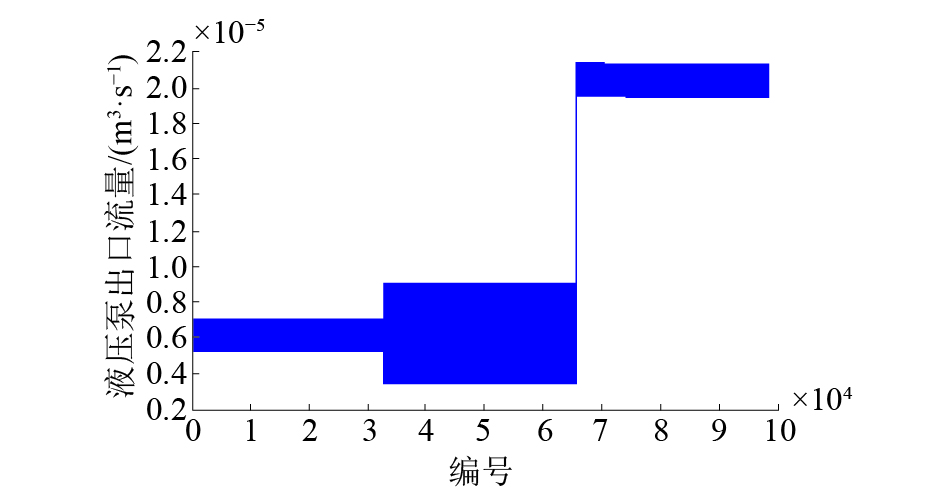
为了验证本文所提出方法的有效性，分别测取了200 s的正常状态、电源电压扰动和泄漏故障3种状态下液压泵仿真模型的出口流量数据，采样频率为512 Hz，截取仿真过程稳定后的128 s数据置于同一图中，如图3所示，得到液压泵不同工作状态下出口流量对比图。

其中编号为0~32 768对应的数据为液压泵正常工作状态的出口流量数据，中间编号32 769~65 536为电源电压扰动故障情况下的流量，而编号65 537~98 304为泄漏故障下的出口流量数据。可以看出正常状态下出口流量波动较小，电源电压存在扰动时出口流量的波动较大，而发生泄漏故障时出口流量很明显的增大了许多。

对所得数据每隔1 s进行一次提取小波包频带能量和计算均方根值和方差的操作。经过上面的流程，以及为这些特征向量进行贴标签的操作之后，得到384个样本，其中正常样本128个，电源电压扰动故障样本128个，泄漏故障样本128个。

表1是其中的部分样本，标签值0表示代表该样本为正常样本，1表示电源电压扰动故障样本，2即泄漏故障样本。本文所用小波变换程序为MATLAB自带的小波包分解工具箱。

得到样本后，将样本均分为两大部分，每部分192个样本，一部分用于SVM的参数寻优和训练，即所谓的训练样本，另一部分用于对训练得到的SVM模型进行准确率测试，即测试样本。

SVM参数优化分别应用网格搜索法和实值遗传算法。网格搜索法步长为1，采用底数为2的幂级数非线性网格，即下一个搜索点值为上一个搜索点值的2倍，搜索范围为 $\left[ {{2^{ - 10}},{2^{10}}} \right]$ ，运行 $20 \times 20 = 400$ 次交叉验证过程，搜索过程中保存最好的结果。遗传算法的交叉概率设置为0.6，变异概率设置0.3，种群大小为20，最大迭代次数为200，当最优适应度值连续5次没有发生变化时，认为找到最优解算法结束退出。这里SVM算法使用的台湾大学林智仁教授编写的LIBSVM库。

实验结果表明两者都可以找到使分类准确率更高更可靠的参数，但本文提出实值编码的遗传算法相对于网格搜索法的穷举具有明显的速度优势，并且在实际编写测试程序时，可以发现实值编码遗传算法相对于二进制等其他编码方式的遗传算法，在算法复杂性上相对简单了很多。在MATLAB R2012b中2种算法分别测试3次，得到运行时间如表2所示。

寻优结束之后，将遗传算法寻优得到的 $c$ 和 $g$ 代入到SVM的训练中，得到SVM模型，然后用该模型诊断测试样本，得到结果如图4所示，可以看出准确达到100%，说明信号特征提取算法得到的特征向量以及GA-SVM也即本文所述方法的有效性和优越性。

5 结论

1)小波包频带能量与时域统计量结合作为代表信号特性的特征向量是一种很有效的表示方法，小波包分解与重构通过再现信号在各小波频谱下的时域波形，可以很好展现出故障在信号不同小波频谱上的表现形式，而时域统计量方差和均方根值则能够大致的区分出不同状态下的信号。

2)SVM只对支撑向量不敏感的特性使其具有强大的推广能力，作者在实验过程中曾提取不同维数的特征向量带入到SVM中训练，都得到了较为满意的结果。需要注意的是信号特征的选取很重要，对于区分度不强的特征，SVM性能和分类准确率有所下降。

3)通过编写实现代码以及实验过程可以很明显地发现，实值编码遗传算法实现上更为稳定和简洁，算法逻辑也更为清晰。

本文提出的以信号频带能量与时域统计量为提出信号特征向量的方法是一种能够提高不同故障情况信号区分度的有效方法，而应用GA-SVM对样本进行自动分类具有较强的推广能力，易于实现并且能够取得较好的实验效果，对相关领域的工作具有一定启发。